一种基于元胞自动机的无线传感器网络安全补丁分发算法

李 林

(天津商业大学信息工程学院，天津 300134)

0 引言

无线传感器网络(wireless sensor networks，WSN)是由大量部署在监测区域内的廉价微型传感器节点组成，通过无线网络传输方式形成的一个多跳的自组织、自适应的智能网络系统[1]，其目的是合作地感知、收集并处理网络覆盖区域的信息，发送给管理者。WSN在各个领域有着广泛的应用[2]。病毒对无线传感器网络而言是一个严峻的安全问题[3-4]。计算机网络中通常采用给计算机系统打上安全补丁的算法来清除病毒，但是对于无线传感器网络，由于其部署量大，节点难以全部回收，必须考虑采用特殊的安全补丁分发算法来清除病毒。

1 模型描述

本文采用正方形网络作为无线传感器网络模型[5]，改进的二维元胞自动机动力学模型描述网络中节点的状态。

1.1 无线传感器网络模型

本文的无线传感器网络模型中，监测区域为一个正方形区域，其边长为l，在监测区域内包含节点个数为n，节点密度为ρ，随机均匀分布在二维区域内，节点信号最大发射距离为r，其可以在距离r内进行通信。这些节点负责感知和采集区域内的数据并通过多跳的方式传输给基站。这些网络节点初始状态下被感染节点的比例为θ，节点成功接收安全补丁概率为α，安全补丁清除病毒的概率为β。

根据网络中节点在网络中的不同状态，网络模型根据节点的特性划分为以下3种状态，如表1所示。

表1 节点状态参数表

1.2 改进的二维元胞自动机模型

元胞自动机是由有限个随机分布的元胞对象组成的离散动态系统[6]。每个元胞都有一个状态，它在每一个时间步的状态根据变化规则进行变化。文中提出的元胞自动机模型通过一个四元组来表示(C，S，N，F)：C表示元胞空间；S表示元胞的状态集；N表示元胞邻域；F为元胞演化规则。二维元胞自动机的安全补丁分发算法包括上述的4部分内容，用式(1)表示：

CAS=(C，S，N，F)

(1)

(1)元胞空间C：这里代表l×l个格子的二维网格，设每个单元最多只容纳一个传感器节点。节点在空间中的位置可以用二维网格中的水平坐标i和垂直坐标j表示；

C={(i,j)|1≤i≤l,1≤j≤l}

(2)

(2)元胞的状态集S：包含两个状态集分别为SC和MAC。其中SC为节点的状态，节点共有3个状态：正常节点状态、已感染状态和获得安全补丁后的免疫状态。当正常节点获得安全补丁后直接进入免疫状态，已感染节点的病毒被清除后进入免疫状态[7]。具体如式(3)所示：

(3)

状态集MAC考虑了无线传感器网络传输中的信道访问原则，分发补丁时采用CSMA/CA方式[8]：当某节点监听到信道忙碌后再随机退避一段时间后进行数据发送，当一个节点在发送数据时其邻域节点均不能发送，只有监听到信道空闲后才会尝试发送数据[9]。具体如式(4)所示；

(4)

(3)元胞邻域：普通的摩尔型邻域[10]如图1所示，灰色部分为K节点的元胞邻域，但由于单个传感器节点的通信覆盖为圆形，不能很好描述网络的真实状态[11]。文中的节点邻域采用改进的扩展型摩尔邻域，剔除了通信距离内无法覆盖的元胞，如图2所示。每个传感器节点最大的发射距离是r，因此任意节点Cij的邻域为

(5)

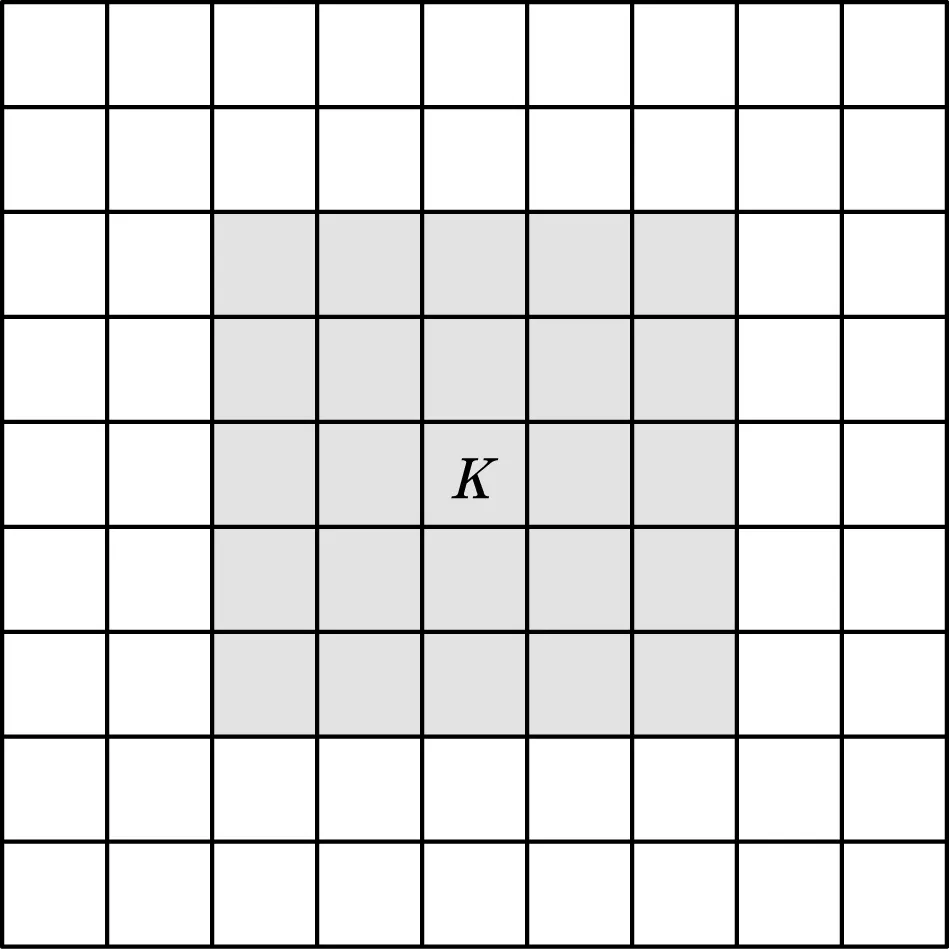
图1 元胞自动机摩尔型邻域

图2 改进型元胞自动机摩尔型邻域

在此模型中，只有属于邻域范围内的节点才可以相互通信。

(4)元胞状态转换函数。节点的状态SCij在t时刻的状态SCij(t)是由t-1时刻节点的状态SCij(t-1)以及其邻域节点的状态集SNij共同决定的，其转换函数可以由式(6)表示：

SCij(t)=F(SCij(t-1)，SNij(t-1))

(6)

若节点在t-1时刻是正常节点状态，状态转换函数为

(7)

式中两个函数的最大值为节点的状态SCij。若这个健康节点邻域有e个获得安全补丁并在免疫状态的节点发送安全补丁包，在这个时间间隔内，有1-(1-α)e的几率收到补丁包，当信道处于空闲状态，则节点进入免疫状态。其中，这个状态转化函数具体描述为

(8)

若节点在t-1时刻是已感染状态。状态转换函数为

(9)

式中两个函数的最大值为节点的状态SCij。若这个节点邻域有e个获得安全补丁并在免疫状态的节点发送安全补丁包，在这个时间间隔内，有1-(1-α)e的几率收到补丁包，当信道处于空闲状态，则节点成功接收到补丁包。每收到一个补丁包后，有β的概率进入免疫状态，则收到g个安全补丁包后治愈的几率为(1-(1-α)e)(1-(1-β)g)，其中g≤e。这个状态转化函数具体描述为

(10)

若节点在t-1时刻已经处在免疫状态,则状态转换函数为

(11)

节点维持此状态不变，仅向外继续分发安全补丁。

2 基于元胞自动机的安全补丁分发算法

基于二维元胞自动机的安全补丁分发算法中，不同节点的工作方式为以下步骤：

2.1 初始节点

(1)l×l正方形区域内，在已知被感染的无线传感器网络中选取一个或若干个节点采取人工烧写程序的方式打上安全补丁，无论节点之前是什么状态，均进入已打上安全补丁的对病毒免疫状态。然后采用二维元胞自动机的方式向外分发安全补丁。

(2)处在免疫状态的节点计算通过式(1)计算自己的状态。

节点在获得安全补丁后其状态为SCij=2，向处在本节点的元胞邻域内的节点分发安全补丁，与邻域内的节点进行通信，节点的邻域为改进的扩展型摩尔型邻域，由式(5)计算。

2.2 病毒感染状态节点

已感染病毒状态的节点通过式(9)计算自己的下一时刻状态。首先探测邻域内的信道状态，若信道空闲，则接收邻域内这些节点发送的补丁包。若这个节点邻域有e个获得安全补丁并在免疫状态的节点发送安全补丁包，在这个时间间隔内，有1-(1-α)e的几率收到补丁包。每收到一个补丁包后，有β的概率进入免疫状态，则收到g个安全补丁包后治愈的几率为(1-(1-α)e)(1-(1-β)g)，其中g≤e。节点若被治愈则进入2.1中(2)步骤，节点若未被治愈，则重复本步骤。

2.3 正常工作节点

正常工作节点通过式(7)来计算自己下一时刻状态。首先探测邻域内的信道状态，若信道空闲，则接收邻域内这些节点发送的补丁包。若这个节点邻域有e个获得安全补丁并在免疫状态的节点发送安全补丁包，在这个时间间隔内，有1-(1-α)e的几率收到补丁包。收到补丁包后，正常节点进行安全升级，免疫病毒侵害，随后进入2.1中(2)步骤。若未收到补丁包则重复此步骤。

令V(t)表示在t时刻已被病毒感染的状态传感器节点的数量占比，R(t)表示在t时刻处于能正常工作但未打上安全补丁状态的传感器节点的数量占比，M(t)表示在t时刻已打上安全补丁对病毒免疫状态的传感器节点的数量占比，由式(12)表示：

(12)

式中V(t)+R(t)+M(t)=1。

经过一段时间，节点采用本文提出的一种基于元胞自动机的安全补丁分发算法将安全补丁分发完毕。

3 仿真

实验网络环境设置如下：监测区域为一个正方形区域，其边长l=200 m，在监测区域内包含节点个数为n，节点密度为ρ，节点的通信距离为r，网络中初始被感染节点的比例为θ，节点成功接收安全补丁概率为α，安全补丁清除病毒的概率为β，每轮单位时间内进行10次通信。

在实验中，研究在无线传感器的不同参数下安全补丁分发效果，初始值节点个数n=20 000，节点密度为ρ=0.5，通信距离r=10 m，初始被感染比例θ=0.4，节点成功接收安全补丁概率α=0.8，安全补丁清除病毒的概率为β=0.6时，将坐标为(100,100)节点打上安全补丁后的V(t)、R(t)、M(t)的曲线如图3所示。实验表明在第23轮后所有节点均已打上安全补丁，本文提出的算法非常高效。

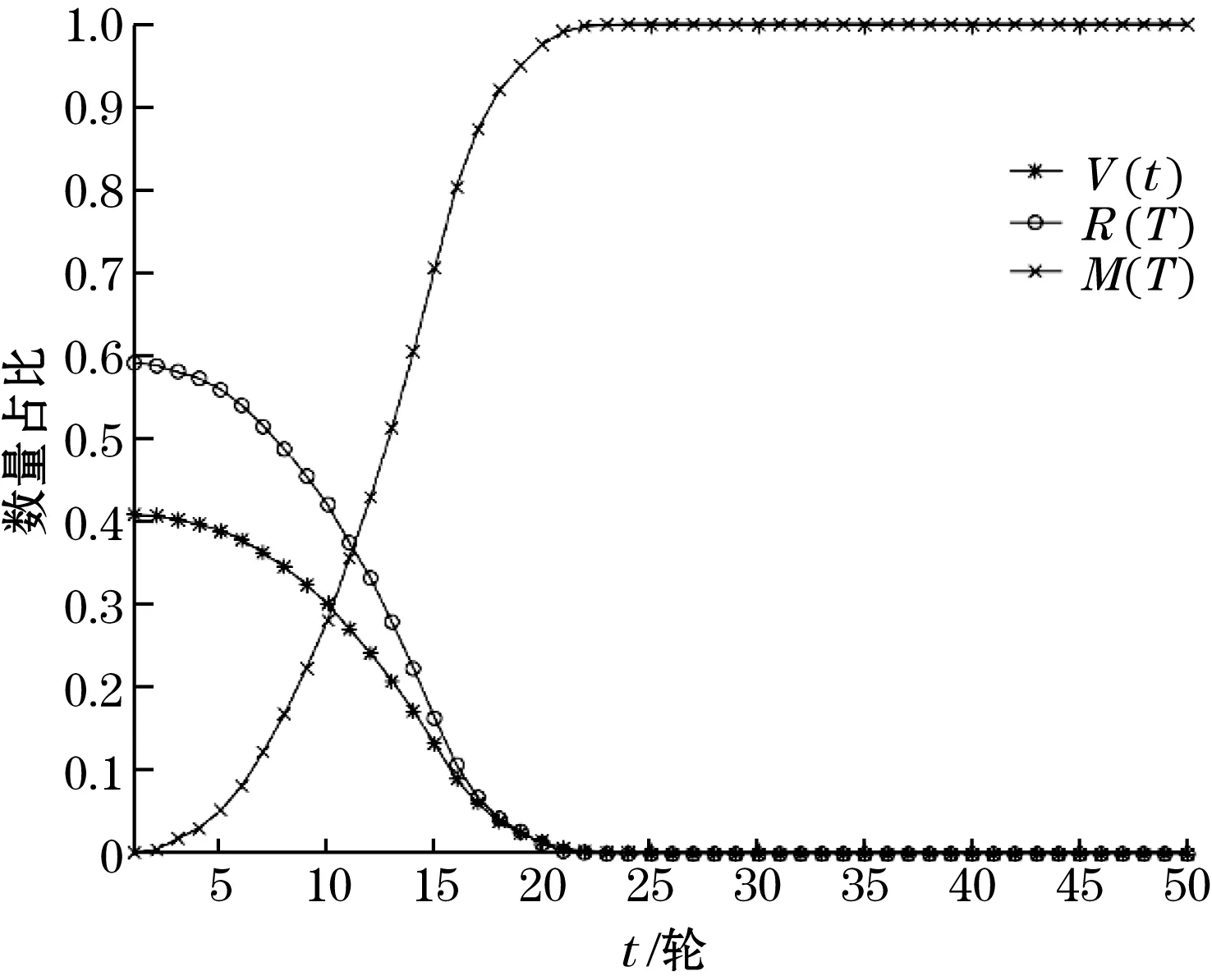
图3 初始参数下补丁分发演化特性曲线

文中研究在安全补丁清除病毒能力较差时的补丁分发效果，取β=0.2。图4表示不同的β取值下的V(t)曲线，图5表示不同取值下的M(t)曲线。该实验表明：当清除能力较差(β=0.2)时，该算法仍能在第30轮将所有节点打上补丁。

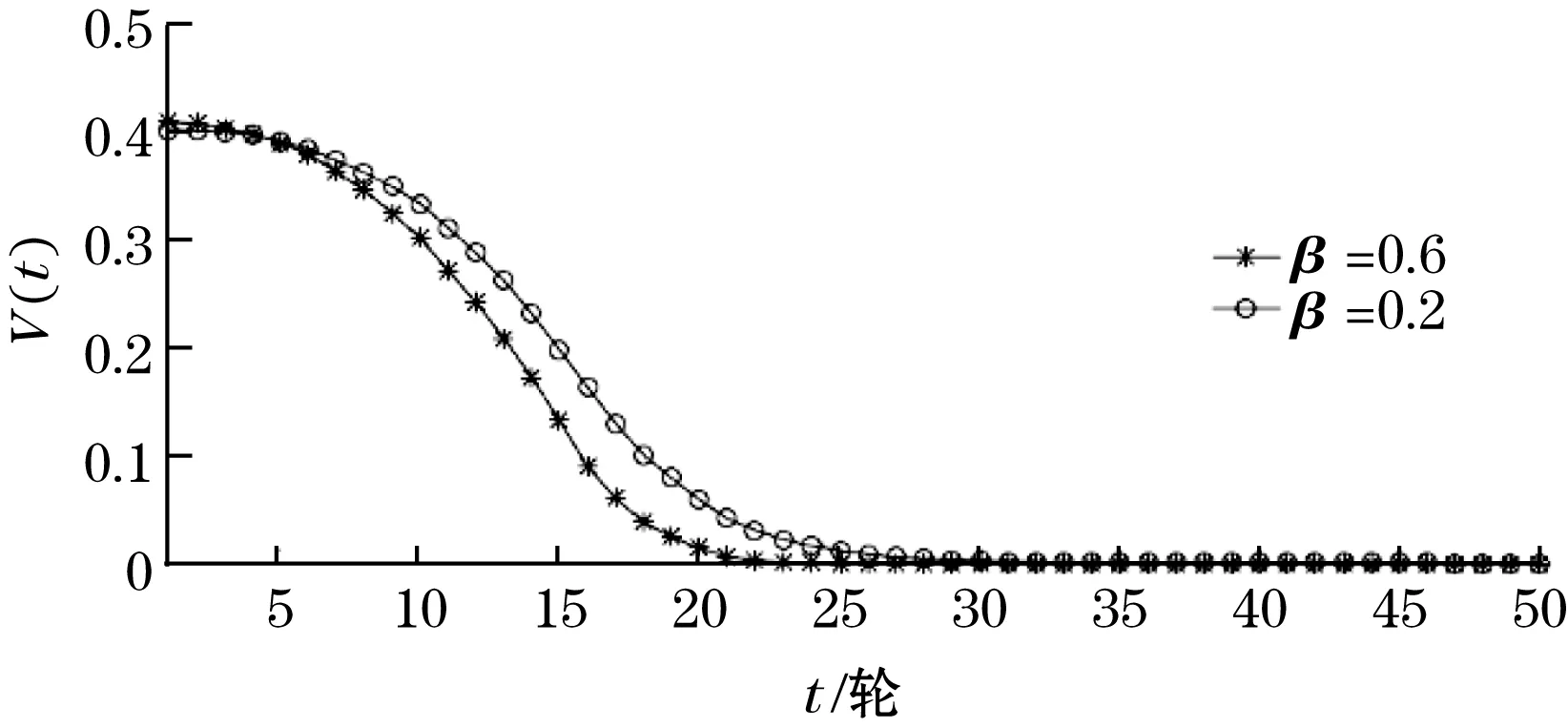
图4 不同β的V(t)曲线

图5 不同β的M(t)曲线

文中研究网络中初始被感染节点的比例较高时补丁分发效果，取θ=0.8。图6表示不同的θ取值下的V(t)曲线，图7表示不同取值下的M(t)曲线。该实验表明：当感染节点在初始被感染节点补丁较高，80%节点都受病毒感染时，该算法可以在第25轮将所有节点打上补丁。

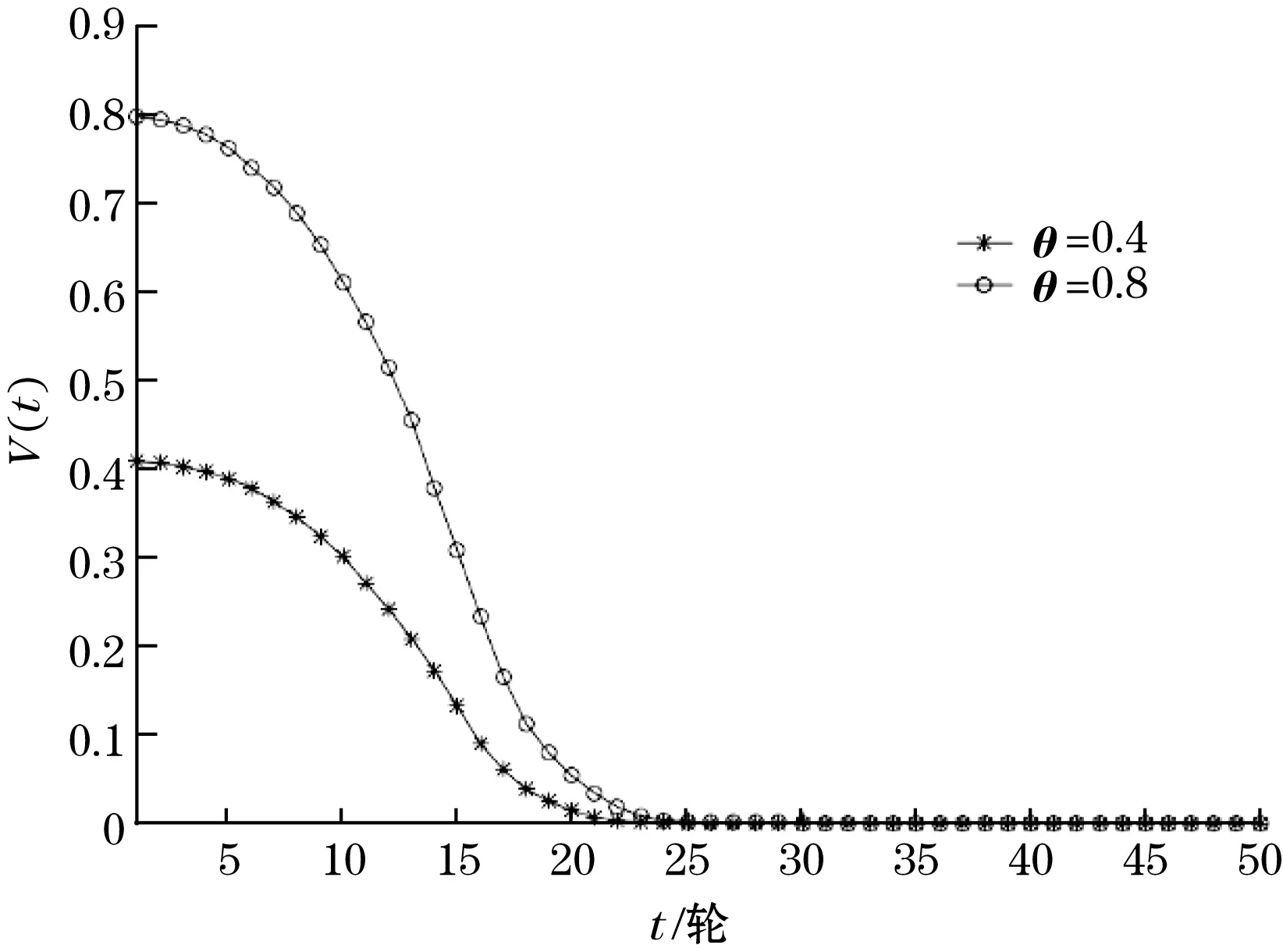
图6 不同θ的V(t)曲线

图7 不同θ的M(t)的曲线

文中研究在不同坐标位置初始节点的分发效果，分别从(100,100)，(50,50)和(10,10)位置开始分发安全补丁，图8表示不同位置取值下的M(t)曲线。实验表明：越靠近区域中心，节点分发补丁的速度越快。但此算法在区域边缘(10,10)的位置仍能在36轮将补丁分发完毕，证明此算法选择区域中任何节点作为初始节点分发安全补丁，最终均能快速将补丁分发完毕。

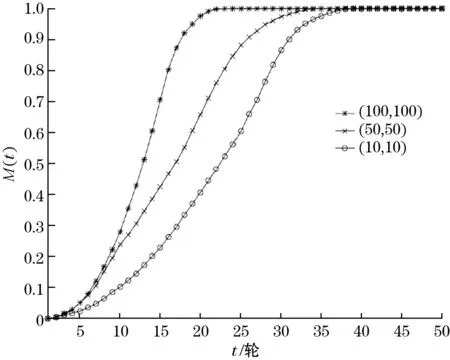
图8 不同位置初始分发节点的M(t)曲线

4 结束语

本文提出了一种基于元胞自动机的无线传感器网络安全补丁分发算法，克服了节点安全补丁难以分发的问题。文中给出了改进的二维元胞自动机安全补丁分发模型以及分发算法的步骤，仿真说明了该算法可以高效快速地将安全补丁分发完毕。