基于前馈补偿PID控制的轮式机器人轨迹跟踪
任鹏飞,赵 楠,王永祥
(河南工程学院 电气信息工程学院,河南 郑州 451191)
轮式机器人在军事、工业、民用等领域应用广泛,其轨迹跟踪控制也是自动控制领域的研究热点。轮式机器人属于典型非线性系统,它的工作环境中存在大量无法预估的外部干扰[1]。由于这些干扰,建立轮式机器人的数学模型有一定难度。
PID控制具有算法简单、鲁棒性高及可靠性高等特点[2],在运动控制和过程控制等领域得到了非常广泛的应用,控制对象的数学模型越精确,控制效果越好。但实际生产过程中的控制对象往往不能建立精确的数学模型,控制过程一般具有非线性、不确定性等特点,所以传统的PID控制效果并不理想[3]。另外,在控制过程中,传统PID的参数整定较复杂、控制性能不佳、适应性差。智能PID利用计算机强大的逻辑计算能力使控制方式更加灵活,为解决上述问题提供了新的选择[4]。采用基于前馈补偿的智能PID方法可以提高轮式机器人的跟踪效果。在经典控制理论中,设法使前馈补偿与闭环系统的传递函数之积为1,就可以实现输出量与输入量相等。
1 建立轮式机器人的数学模型
对轮式机器人的驱动和转向控制有多种方式。本研究的控制对象是四轮式机器人,其转向轮为两前轮,可以控制机器人的行进方向;其驱动轮为两后轮,可以驱动机器人前进、后退。驱动轮可采用单电机配合机械差速机构实现驱动,还可以采用双电机差速方式实现驱动。本研究的对象是驱动轮双电机差速方式,运动示意图如图1所示。轮式机器人的实时位置状态可用两驱动轮轴中点M及其前进方向角θ描述[5]。
从图1中可以看出,若令P=[xyθ]T,q=[vω]T,可根据[xy]定位轮式机器人的坐标,θ表示机器人的前进方向与x轴的夹角,v和ω表示轮式机器人的线速度和角速度,这些参数可作为轮式机器人控制的输入信号。

图1 轮式机器人运动示意图Fig.1 Motion diagram of wheeled robot
根据以上信息可构建轮式机器人的运动方程:

(1)
由方程(1)可得轮式机器人的数学模型为

(2)
从方程(1)可以看出,该机器人的数学模型为2自由度,输出变量为3个,该模型是欠驱动系统,可实现2个变量的跟踪,剩余变量为状态随动或镇定状态。本研究中,轮式机器人的轨迹跟踪可通过设计q=[vω]T来实现对位置坐标[xy]的跟踪,并实现θ随动。
2 双闭环系统设计
构建一个双闭环的控制系统,包括外环位置子系统和内环姿态子系统。外环位置子系统控制器的指令信号θd传送给内环姿态子系统控制器,内环通过滑膜控制来实现对指令信号θd的跟踪。该双闭环系统的结构如图2所示。
为保证闭环系统的稳定性,控制工程中通常采用外环收敛速度小于内环收敛速度的办法,来增大控制器增益,用θ来跟踪θd。
3 轮式机器人位置控制设计
通过对轮式机器人位置的确定,对其位置控制规律v进行设计,用x跟踪xd,用y跟踪yd。设定其理想目标轨迹是[xdyd],其误差跟踪方程为
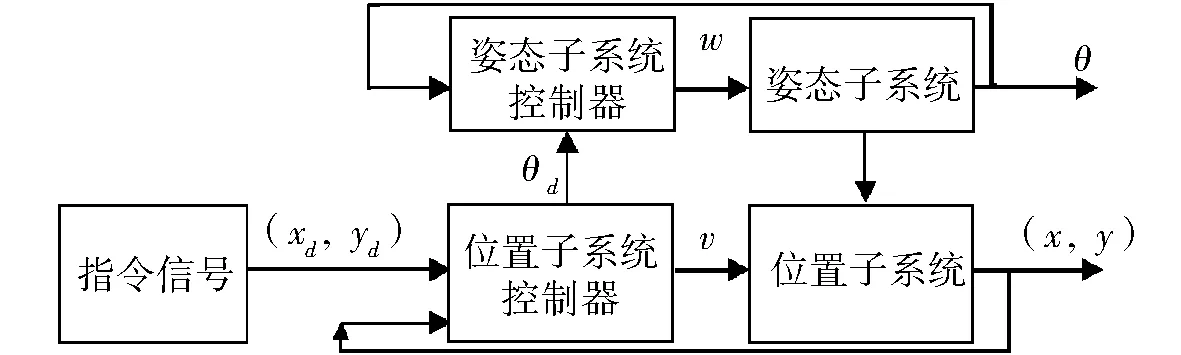
图2 双闭环控制系统结构Fig.2 Structure diagram of double closed loop control system
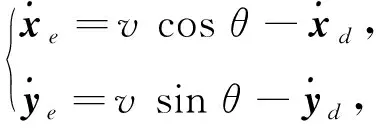
(3)
式中:xe=x-xd;ye=y-yd。取
(4)
(5)
根据公式(6)前馈控制规律可得公式(7):
(6)
(7)
式中:kp10。则t趋近于无穷时,xe趋近于0。
(8)
根据公式(9)前馈控制规律可得公式(10):
(9)
(10)
式中:kp20。则t趋近于无穷时,ye趋近于0。
(11)
式中:θ为公式(6)和公式(9)所期望的角度。如果θ=θd,即可实现公式(6)等价于公式(9)。但在控制刚开始的阶段,实际模型公式(2)中的θ不完全等于θd,这会直接造成公式(3)不稳定。
若想解决以上问题,需要设定公式(11)中求得的θ为目标值,可得
(12)

经上述推导,得出轮式机器人位置控制规律为
(13)
4 轮式机器人姿态控制设计
对轮式机器人的姿态控制可通过对其姿态控制规律ω的设计实现,最终实现θ跟踪θd的目的。
令θe=θ-θd,可得式(14),根据式(15)前馈控制规律可得式(16):
(14)
(15)
(16)
式中:kp30。则t趋近于无穷时,θe趋近于0,最终实现θ对θd的快速跟踪。
5 仿真验证

图3 系统仿真模型Fig.3 System simulation model
为了证实该控制方案的有效性,采用MATLAB仿真方式来验证。依照图2所示的双闭环控制系统结构,可在MATLAB/Simulink环境中建立系统仿真模型,如图3所示。
控制器参数设定值见表1。按表1设定控制器各参数,在MATLAB中可得仿真结果,如图4至图6所示。

表1 控制器参数设定值Tab.1 Controller parameter settings
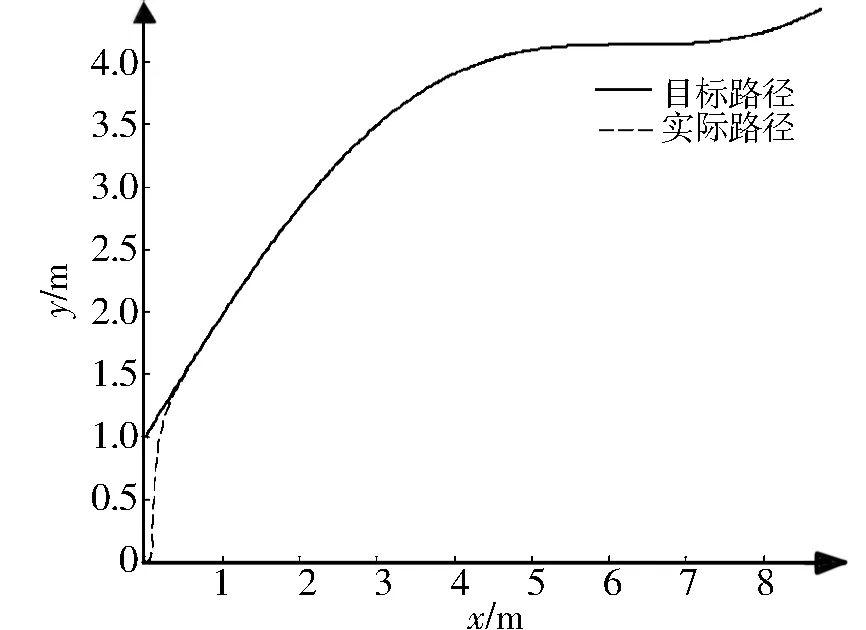
图4 轮式机器人轨迹跟踪Fig.4 Wheeled robot trajectory tracking
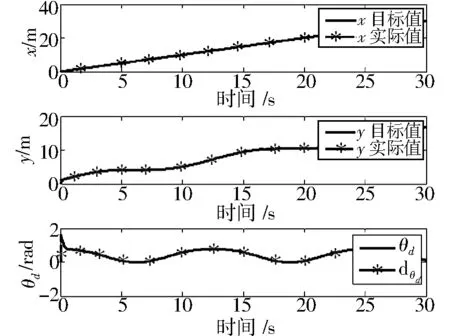
图5 位置和角速度跟踪Fig.5 Position and angular velocity tracking
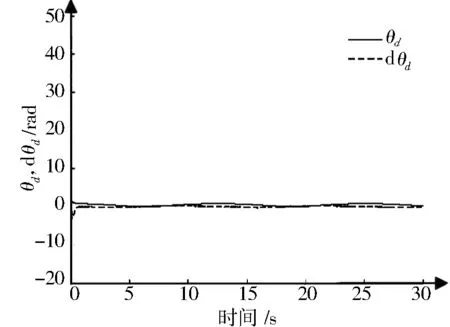
图6 微分器输入与输出Fig.6 The input and output of differentiator
图4为轮式机器人位置轨迹跟踪结果,可看出轮式机器人对外部扰动不敏感,能达到并保持目标位置。
图5为轮式机器人位置和角速度跟踪结果,可看出仅经过5 s,轮式机器人即达到目标位置并保持稳定,仿真输出结果小幅抖动与外界干扰项有关。
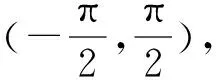
6 结语
针对轮式机器人在其运行过程中出现的不可控扰动问题,提出了前馈补偿控制器设计,从而保证系统的稳定性。由仿真结果可知,该控制器可快速稳定地实现轮式机器人的轨迹跟踪控制,有效减少了扰动不可控现象对跟踪性能的影响。

