高斯方程优化的电磁发射系统设计
李小魁,孙登俊,王锦浩,周 林
(河南工程学院 电气信息工程学院,河南 郑州 451191)
电磁发射是武器发射技术的新主题,线圈炮是电磁发射武器众多种类中的典型代表之一。电磁炮的发射原理是以模拟电磁线圈炮为模型,利用直流电给线圈供电产生电磁场,通过安培力推动弹丸加速从而发射出去。在发射过程中,炮管中会产生摩擦、抖动等影响弹丸的飞行轨迹,需要制定一个好的制导律引导弹丸准确击中目标[1]。
为实现对炮弹弹道的有效跟踪,杨志豪等[2]开发了一种基于弹道成型制导律的末制导方案。为实现导弹质点运动模型的精确线性化,张大元等[3]基于反馈线性化理论设计了一种弹道跟踪制导律。为解决控制精度和抖振问题,杨荣军等[4]通过设计弹道制导跟踪控制器,再利用李雅普诺夫理论和仿真,验证了弹道制导需要考虑气动参数误差与外部扰动。既有方案解决了弹道制导律的精确线性化、弹道有效跟踪的问题,但快速生成仿真弹道及实现精确打击的问题还需要进一步解决。
本研究提出通过高斯方程优化快速计算出的模拟弹道数据制作电磁炮系统,在随机干扰的情况下,电磁炮实际轨迹方向能够达到目标区域,炮弹能够在制导弹道末端以弹着角大于π/4的弧度命中目标。经过多次实验,该系统能够满足对弹道曲线快速拟合、确定终端位置和弹着角约束的要求,并能准确地击中目标。
1 系统方案
以STM32F429IGT6型芯片作为控制核心与摄像头和激光测距模块连接,处理接收到的图像,检测靶标位置并确定距离,OLED液晶屏幕显示相应信息,通过PID算法调整PWM占空比,实现控制云台对炮筒角度调整进而精准打击目标。系统整体框图如图1所示。
1.1 机械结构设计
电磁炮系统模型由底座、舵机、支架、炮筒等部分组成。舵机组成云台,其左右活动角度为±135°,上下活动角度为0°~135°。为满足弹着角约束,炮管角度调整为61.95°(纵向舵机脉冲宽度为959 μs)到76.14°(纵向舵机脉冲宽度为1 064 μs)。电磁炮系统结构如图2所示。
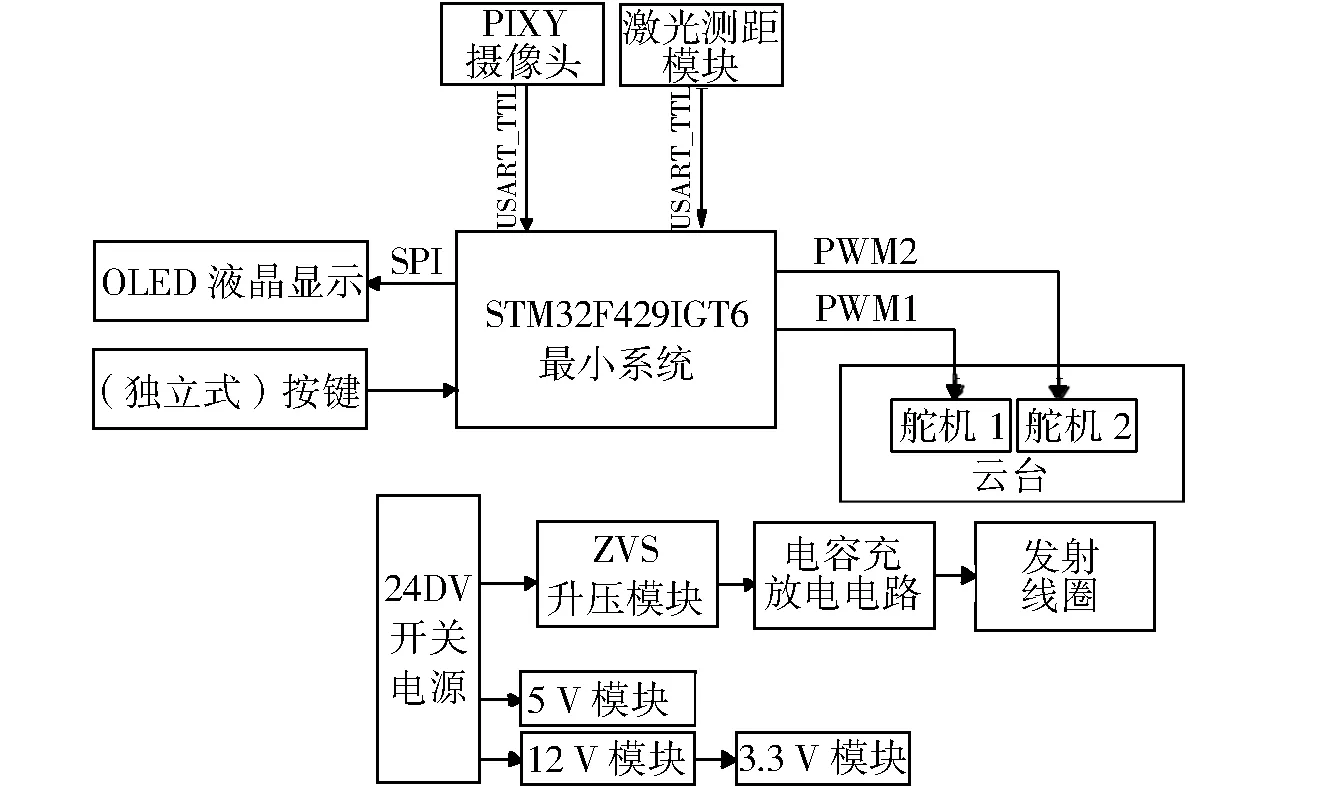
图1 系统整体框图Fig.1 System block diagram

图2 系统结构Fig.2 System structure
1.2 主控部分和电源设计
采用以ARM Cortex-M4为内核的STM32F429IGT6型控制芯片,该芯片时钟频率高达90 MHz,具有2 MB的闪存、256+4 KB的SRAM,包括64 KB的CCM数据RAM,拥有丰富且强大的I/O口,具有强大的计算处理能力,适合需要快速精确计算结果的电磁曲射炮系统。考虑系统的稳定性和经济性,使用24 V开关电源通过DC-DC转换为12 V电压、5 V电压和3.3 V电压,12 V电压提供给STM32系统板,在板内12 V电压转换为3.3 V为MCU供电,5 V电压提供给云台舵机,24 V电压接给ZVS升压模块为发射装置供电。
1.3 传感器的选择
采用PIXY视觉传感器和激光测距模块检测靶标位置,使用视觉传感器检测靶标的方向,用激光测距模块确定距离,进而确定炮筒的左右角度和仰角。PIXY视觉传感器具有像素高、输出帧率高等优点,可配合STM32F429IGT6型控制芯片确定靶标的位置;激光测距系统在20 m内误差非常小,可以忽略不计。
2 算法分析与程序设计
2.1 制导方程算法构建
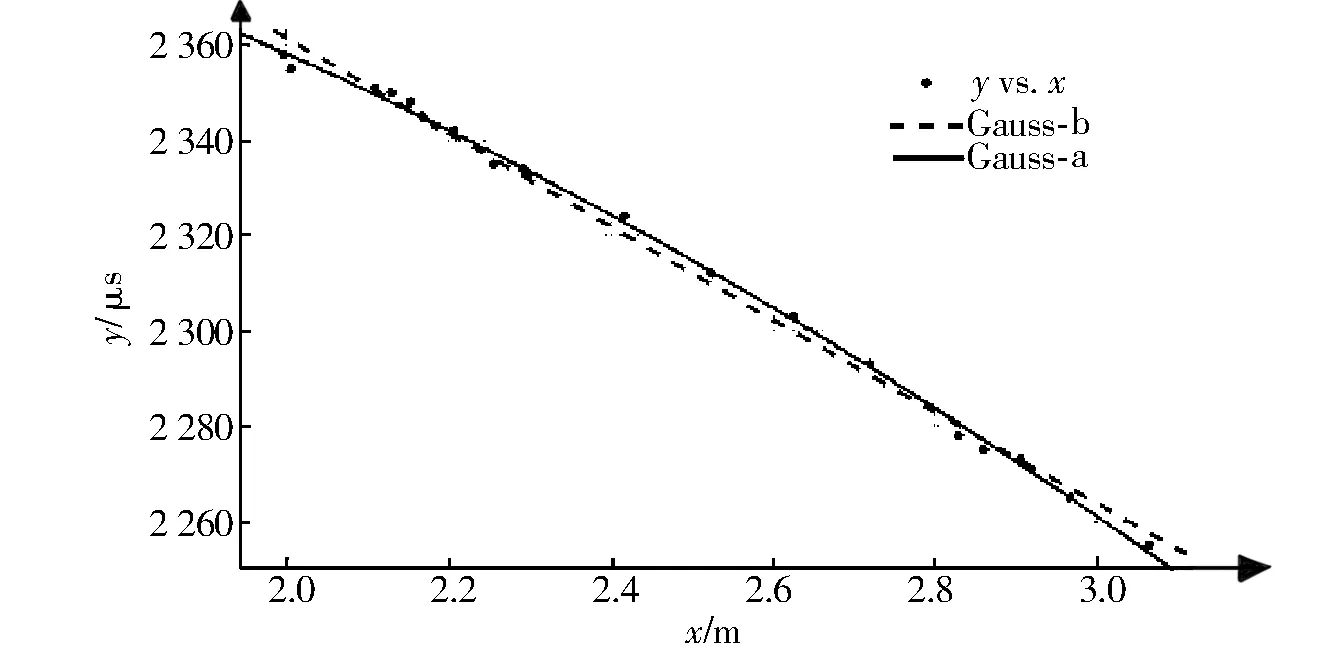
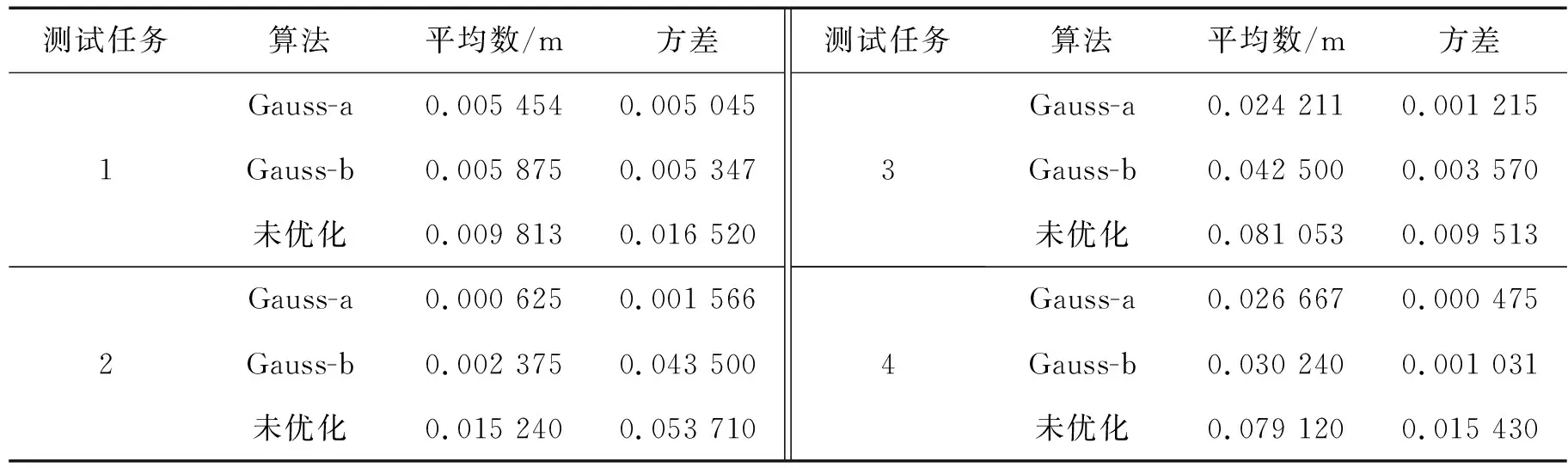
电磁炮的弹道是一个多变量、非线性的控制系统。在调节炮筒的角度时,没有一个准确的关系来确定控制舵机的角度与发射距离。分析弹道特征点将弹道分段,所需弹道缩放系数和曲线拟合系数可通过少量初始数据确定。缩放系数可以在设定发射位置和目标位置之后确定,发射位置到目标位置的地面距离表示为Sqw,必须满足Smin (1) 对各特征点进行计算,可得线性插值方程如下: x=xk+L(xk+1-xk), (2) 式中:x表示拟合轨迹数据;xk表示小于目标射程的边界轨迹数据;xk+1表示大于目标射程的边界轨迹数据。计算射程拟合方程的系数矩阵Sc和高度拟合方程的系数矩阵Hc: (3) 式中:SI和SI+1表示分段弹道中2个特征点的射程值;HI和HI+1表示分段弹道中2个特征点的高度值。然后,构建拟合方程: (4) 进而拟合弹道曲线,得出弹道射程S、高度H、弹道倾角θ[5-6],再根据这些参数拟合弹道进行大量实验,将得到的发射距离进行加权取平均,结果见表1。 表1 不同PWM脉宽对应的炮弹发射距离Tab.1 Cannonball firing distance corresponding to different PWM pulse widths 利用高斯伪谱法能以较少参考点获得较高精度的优点,将弹道分段的特征值作为离散点逐渐逼近控制问题的控制变量(X0,X1,…,Xk)和状态变量(U1,…,Uk),将微分方程约束转换为代数约束得到的最优轨迹与数值积分得到的最优轨迹相比误差很小,且具有很高的边界控制精度[7-8]。结合表1数据列出考虑系统发射抖振误差的高斯优化方程(5)Gauss-a与不考虑系统发射抖振误差的优化方程(6)Gauss-b: (5) y=a·ebx, (6) 式(5)中:a为发射角度限定值;b为发射抖振误差系数;c为系统尺度参数。 式(6)中:a为发射角度限定值;b为系统尺度参数。 将2个优化方程在上述拟合弹道射程范围内的规划曲线和表1数据相结合,得到如图3所示的高斯方程优化曲线。 图3 高斯方程优化曲线Fig.3 Gaussian equation optimization curve 图3中,实线表示式(5)在拟合弹道射程范围所成图像,虚线表示式(6)在拟合弹道射程范围所成图像,散点表示未经过优化的拟合弹道在发射测试中所得数据在图像中的分布。 本模型系统执行机构为DS3115舵机组成的云台,通过PID算法控制PWM脉宽可以控制舵机的转动角度,以改变炮筒的方向和发射角度。在实际运行中,舵机依然会出现误差。为提高云台的运动特性,提前预判云台输出,减少舵机转角跟踪误差,采用微分先行的双闭环舵机控制策略,所设计的PID控制系统[9-10]如图4所示。 系统在数据输入和模式转换时采用了6个独立按键,利用OLED液晶屏显示相应信息。系统初始化后,检测按键,选择不同的模式,执行相应部分的程序。程序流程如图5所示。 图4 PID控制系统框图Fig.4 PID control system block diagram 图5 程序流程Fig.5 Program flow chart 根据表1所得的结果,在实验室搭建发射环境,场地长约4 m、宽约2.5 m。发射环境规划好相应的角度与距离,对考虑抖振误差和未考虑抖振误差的高斯优化方程与未经过优化的弹道制导方程进行测试。 测试任务1:将目标靶距离发射点 2~3 m,利用独立键盘输入距离,启动后,电磁炮发射。测试任务2:用键盘给电磁炮输入目标靶与发射点的距离及与中心线的偏离角度,启动后,电磁炮自动瞄准射击。测试任务3:将目标靶放置在距离发射点250 cm的位置,引导标识处于两物延长线位置,电磁炮放置在发射点自动搜寻目标并炮击目标靶。测试任务4:在攻击范围任意位置放置目标靶,一键启动后,电磁炮自动搜寻目标并炮击环形靶。 统计测试过程中实际发射距离与目标距离的差所得的平均数(以下简称“平均数”)和方差,确定精准度和稳定性,结果如表2所示。 表2 测试结果Tab.2 Test results 分别对得到的误差平均数和方差进行拟合比较,得出如图6和图7所示的折线图。 图6 测试结果误差平均值Fig.6 The mean error of the test results 图7 测试结果方差Fig.7 The variance of the test results 从表2与图6可以看出:高斯方程优化后,误差从未优化制导律的8%降到了4%以内。从表2与图7可得出:高斯方程优化后,最大方差从优化前的0.055降到了0.045,稳定性提升了22%。高斯优化方程制导律在考虑抖振问题的情况下,最大误差从未考虑抖振问题时的4%精确到3%,而方差从最大值0.043降为0.005,稳定性提升了86%。 综合以上结果,与未经过优化的制导律相比,高斯优化方程在准确性和稳定性方面更加优越。在高斯方程优化测试中,2种优化方程所得误差平均值虽有部分较为接近,但是综合考虑抖振误差的优化方程测试结果更加精准,同时在稳定性方面也更加优越。 本研究针对电磁炮模型系统的制作和发射性能和制导律优化进行了阐述。在构建制导方程时,建立弹道拟合方程,得到模拟弹道曲线,再引入高斯卷积方程进行弹道优化与制导,采用激光测距模块和PIXY视觉传感器获取目标位置信息,实现了电磁炮模型系统能够手动发射和自动检测目标信息且快速、准确地击中目标,并保证系统运行过程中具有良好的鲁棒性。
2.2 执行机构算法与驱动
2.3 总体程序流程


3 测试方案与测试结果


4 结语

