空气流量下易燃煤层采空区遗煤氧化升温特性研究
左秋玲,李景山
(1.河南工程学院 安全工程学院,河南 郑州 451191;2.铁道警察学院 治安学系,河南 郑州 450053)
随着矿井开采深度的增加,回采面会突然涌出大量瓦斯,上隅角和回风流中出现的瓦斯超限都是导致瓦斯事故频发的常见因素。大多矿井采用加大风量的方法来稀释瓦斯,但这样会增加工作面两端的压差,在一定程度上增加了采空区的漏风,使得易自燃煤层采空区的破碎煤体更易自燃。
国内外学者针对煤矿采空区的自燃做了大量的研究,主要集中在以下几个方面:采空区煤自燃的实验研究[1-8]、自燃机制[9-13]、采空区自燃的各种数值模拟与分析[14]和煤自燃风险分析[15-16]。目前在漏风量对煤氧化影响的实验方面,漏风量均采用均匀漏风,按一定的梯度逐步增加,且漏风通道只有一处,无法满足采空区漏风通道的实验要求。基于上述分析,不同漏风量对深部矿井易燃煤层采空区遗煤自燃的影响亟须研究。本研究基于九宫格原理,设计了采空区的3种漏风通道和空气流量,开展易自燃煤层采空区煤自燃升温氧化实验,研究不同空气流量下采空区遗煤的升温氧化过程及规律,得出不同漏风量对采空区煤自燃的影响程度。
1 实验系统设计
1.1 实验煤样的制备
本实验煤样取自河南省永锦能源公司云盖山煤矿一矿(以下简称“云煤一矿”)。云煤一矿位于河南省许昌市禹州市磨街乡佛山村,被评测为高瓦斯矿井。实验前对煤样进行处理,采用网筛对煤样进行筛选,煤样参数如表1所示。

表1 实验煤样参数Tab.1 Parameters of experimental coal sample
1.2 实验系统元件参数
实验所用元件及其参数如下:采空区煤自燃实验系统(15 cm×15 cm×10 cm)、三脚燃烧台(h=15 cm)、石棉网(d=20 cm)、带微孔的封闭罩(16 cm×16 cm×5 cm) 、热电偶(3个)、CO气体浓度检测仪(1个)、供风装置(1个)。实验系统示意图见图1。
1.3 实验流程
(1)将实验煤样堆成15 cm×15 cm×8 cm的长方体,然后在长方体煤样内部沿中性面每隔2 cm设置一个测温探头,自下至上依次记为A、B、C,在煤样内均匀分布,以准确掌握实验过程中煤样各点温度变化。测温探头位置如图2所示。

图1 实验系统示意图Fig.1 Schematic diagram of experimental system

图2 测温点分布情况Fig.2 Distribution of temperature measurement points
(2)用带微孔的密封罩将采空区煤自燃实验台封闭,微孔按照九宫格设置,每小格设置3个微孔进行供风。
(3)对煤样进行间接加热,打开风扇对微孔进行供风,模拟3种漏风情况,测试其内部温度和CO浓度的变化。
(4)煤样下部A点温度升高至自燃点80 ℃时,停止外部供热。
(5)记录1 h内每1 s实验煤样温度、CO浓度和O2浓度的变化,每组数据4 000个,处理数据时每隔100 s选取一个,共40组。
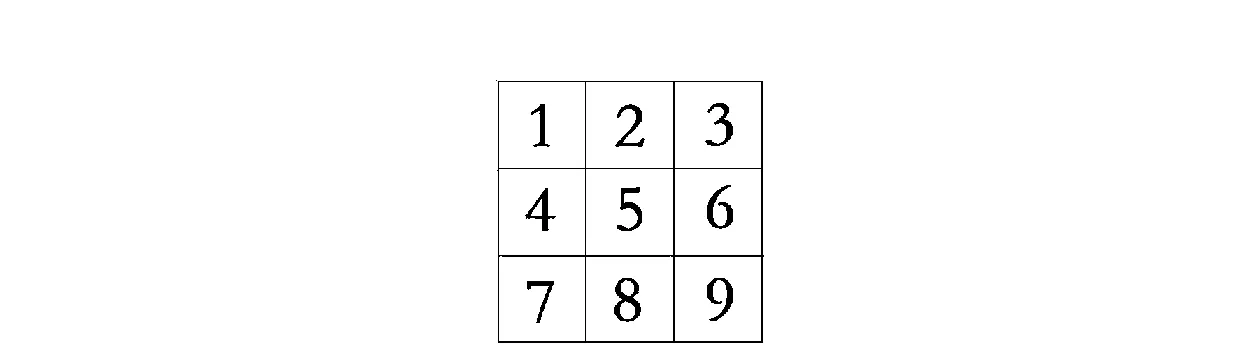
图3 密闭罩微孔九宫格分布情况Fig.3 Sudoku distribution of micro-hole in airtight cover
2 基于九宫格原理的漏风通道设计
由上述实验流程可知,需要通过逐步改变封闭罩的微孔分布来改变漏风量,故将微孔密闭罩按照九宫格划分,具体见图3。选取3个区域模拟不同漏风通道:区域一(4—5—6),区域二(1—3—5—7—9),区域三(1—2—3—4—5—6—7—8—9)。使用风速计测得每个小格的平均风速,然后推算出各区域的平均风速,结果如表2所示。

表2 模拟漏风通道下断面风速Tab.2 Simulation wind velocity of cross-section under air leakage passage m/s
微孔密闭罩的微孔直径为2 mm,平均每小格分布3个微孔,则每小格的漏风面积
S=3.14×r2×3=9.42×10-6m2。
(1)
模拟漏风条件时漏风量的计算公式如下:
qV=V·S,
(2)
式中:qV为漏风量,m3/s;v为通过断面的平均风速,m/s;S为断面的面积,m2。
实验时通过打开微孔密闭罩不同数量的区域来改变漏风量,漏风量如表3所示。

表3 漏风量Tab.3 Air leakage rate
3 结果与分析
研究漏风量与煤自燃特性的变化特征需要从耗氧速率VO2(T)和放热强度q两个方面入手。
3.1 耗氧速率
采用两种方式计算耗氧速率。一种是
(3)
式中:qV为漏风通道的漏风量,10-6m3/s;φ1为进口处氧气体积分数,常取20.9%;φ2为出口处氧气体积分数,%;L为实验采空区腔体的内部高度,cm;S为实验采空区横截面积,cm2;n为实验煤样空隙率,取0.45。代入实验数据,得到不同漏风量下煤样的耗氧速率与煤温的变化规律。不同漏风量下耗氧速率变化曲线1见图4。
由图4可以得出:(1)耗氧速率与漏风量存在类似的关系,有3次较为明显的峰值。第一次峰值出现在48 ℃左右,在实验腔体内煤氧化的初始阶段,生成的热量要小于其向外界放出的热量。第二次峰值出现在75 ℃左右,这时候实验煤样基本进入氧化的第二个阶段——自燃阶段,可以看出耗氧速度的变化量比较明显,但随着采空区漏风量的影响,实验煤样并没有直接进入第三阶段——燃烧,而是呈现下降的趋势。这是因为进入的空气流量会降低实验腔体内的温度,但由于煤的氧化放热占据主导位置,所以使得第三次峰值出现在105 ℃左右,实验煤样开始燃烧,随着煤样的消耗,对外界的放热又占据主导地位,故耗氧速率开始急剧下降。(2)小空气流量下,峰值的变化较平缓且3次峰值下的温度均最低,但和其他空气流量相比,峰值出现的温度均变化不大,说明空气流量的变化对耗氧速率峰值波动的影响不明显。(3)不同空气流量下,3次耗氧速率的峰值均与空气流量密切相关,空气流量越大,耗氧速率峰值越高且峰值差也越来越大。因为空气流量大,说明供氧充分,更利于实验煤样的氧化。
另一种是徐精彩[17]的公式:
(4)

由图5可以得出:(1)利用第二种方法计算出的耗氧速率与漏风量的关系与图4类似,同样有3个峰值出现。(2)大空气流量下,耗氧速率的3次峰值均高于用第一种方法计算出的耗氧速率,这说明空隙率对煤样自燃的影响比较明显,不可忽略。在空气流量为165.8×10-6cm3/s和295.8×10-6cm3/s时,耗氧速率的3次峰值均比用第一种方法计算出的值要小得多,但当空气流量为97.78×10-6cm3/s时,耗氧速率峰值的差别不大,这说明当空气流量比较小时,对实验腔体内煤样的自燃影响不大。
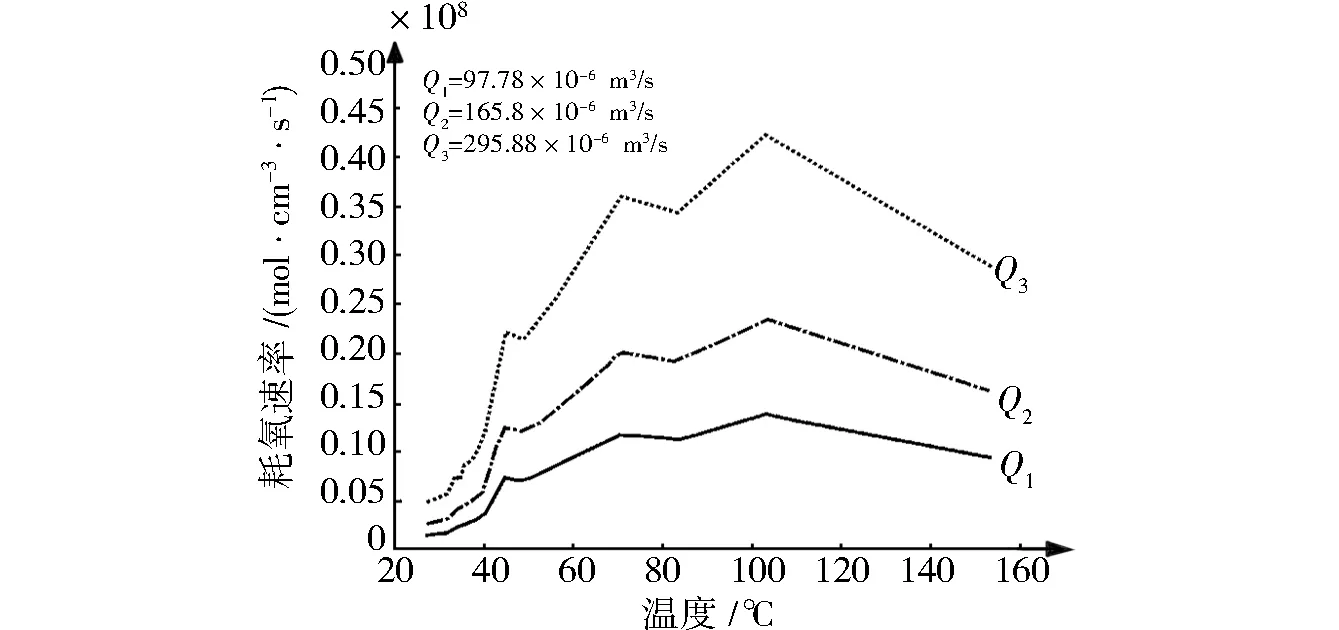
图4 不同漏风量下耗氧速率变化曲线1Fig.4 The change curve 1 of oxygen consumption rate under different air leakage rates

图5 不同漏风量下耗氧速率变化曲线2Fig.5 Change curve 2 of oxygen consumption rate under different air leakage rates
3.2 放热强度
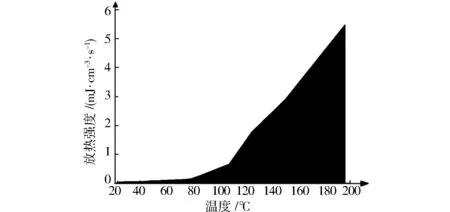
煤在低温阶段,其煤氧复合升温比较缓慢,产生的热量q0很小。放热强度q0(T)的计算方法有两种:热平衡法q0(T)和键能估算法(qmin(T),qmax(T))。这两种方法所推导出的氧化放热强度q0(T)的关系为qmin(T) 假定本实验腔体内流经堆积煤体的Tair=Tcoal,风流沿纵轴流动,在忽略其他热量交换的前提下,煤氧化过程中的热量交换只考虑煤的氧化放热、腔体壁面传导散热和腔体内流经风流的对流散热,实验腔体内热量场交换见图6。 实验腔体中心处的热平衡方程[18]如下: (5) (6) ce=ncg+(1-n)cm, (7) ρe=nρg+(1-n)ρm, (8) 低温氧化阶段,煤的氧化放热强度q(T)与氧气体积分数φ成正比,其标准氧气体积分数下的氧化放热强度 q0(T)=(φ0/φ1)q(T)。 (9) 实验煤样放热强度变化见图7。由图7可以得出:(1)当温度达到80 ℃左右时,利用热平衡法计算出的放热强度与温度呈现指数变化的关系;(2)80 ℃之前,煤样的放热并不多,放热强度几乎没有变化,这说明在此之前,煤样均处于积累热量与放出热量互相博弈的阶段;(3)80 ℃之后,实验煤样的放热强度呈现指数变化,生成的热量占据主导地位,远远大于与外界的热交换,放热强度急剧升高。 图6 实验腔体热量交换关系Fig.6 Heat exchange diagram of experimental chamber 图7 实验煤样放热强度变化Fig.7 Variation diagram of exothermic intensity of experimental coal sample (1)模拟漏风通道的设计和风速的确定。逐步改变封闭罩的微孔分布以改变漏风量,密闭罩微孔按照九宫格划分,选取3个区域作为模拟漏风通道,根据每个小格的平均风速推算出实验区域的平均风速。 (2)比较了目前使用的两种耗氧速率计算方法。考虑煤样空隙率,耗氧速率有3次较为明显的峰值,第一次峰值出现在48 ℃左右,第二次峰值出现在75 ℃左右,第三次峰值出现在105 ℃左右;小空气流量下,峰值的变化较平缓且3次峰值下的温度均最低;不同空气流量下,3次耗氧速率的峰值均与空气流量密切相关,空气流量越大,耗氧速率峰值越高且峰值差也越来越大。不考虑煤样空隙率,大空气流量下,耗氧速率的3次峰值均高于用第一种方法计算出的耗氧速率。在小空气流量下,耗氧速率的峰值差别不大,说明当空气流量较小时,对实验腔体内煤样的自燃影响不大。 (3)利用热平衡法计算了放热强度与温度之间的关系。80 ℃之前,煤样的放热并不多,放热强度几乎没有变化;80 ℃之后,实验煤样生成的热量开始占据主导地位,远远大于与外界的热交换,呈指数变化,放热强度急剧升高。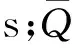
4 结论

