基于神经网络MM247合金冷却速率与力学性能的研究
郭 雄 高振桓 史卫杰 陶 飞 杨照宏
(1.东方电气集团东方汽轮机有限公司,四川618000;2.长寿命高温材料国家重点实验室,四川618000)
MM247铸造高温合金因其良好的高温拉伸持久、抗蠕变、抗热腐蚀性能而被广泛地应用于燃机透平叶片。其优良的综合性能主要得益于各合金化元素对组织的沉淀强化、晶界强化及固溶强化作用。由于合金加入的化学元素种类较多,其相组成变得尤为复杂,且组织结构间相互影响。目前,针对MM247高温合金的研究主要集中在以下几方面:(1)化学成分对相结构、组织的影响[1-2];(2)组织对合金的强化机理研究[3-4];(3)凝固参数或工艺参数对相结构、组织的影响[5-7];(4)高温合金性能评价[8]。应当在工艺设计初端就充分考虑凝固组织状态,以性能为导向进行工艺设计。
众所周知,凝固组织决定着力学性能,但凝固组织又与凝固参数冷却速率密切相关,工艺参数如浇注温度、型壳预热温度等直接决定着冷却速率的大小。因此,要想研究冷却速率与性能的关系,就必须先研究凝固组织与冷却速率的关系、以及凝固组织与力学性能的对应关系。由于高温合金凝固组织错综复杂,本文将以人工神经网络求解凝固组织与冷却速率的非线性关系,并拟合计算冷却速率与力学性能的关系,为工艺设计提供理论支撑。
1 实验内容及方法
1.1 研究对象及内容
本文以某燃机动叶片为研究对象,通过ProCAST铸造软件计算并选取了动叶片不同壁厚位置的冷却速率。同时,对叶片进行精铸实验,并解剖相应位置,获取凝固组织信息。随后,采用MATLAB软件,对凝固组织与冷却速率进行神经网络建模、训练和验证,并最终用于冷却速率的预测。
除此之外,选取额外的若干试样进行力学性能测试,获取室温拉伸性能,并解剖该试样,观测凝固组织并利用训练好的神经网络进行冷却速率的预测,建立冷却速率与性能的关系。
本文采用的MM247合金,其名义成分(质量分数,%)为:Cr 8.2,Co 9.2,Mo 0.5,W 9.4,Al 5.6,Ta 3.2,Ti 0.7,C 0.08,Hf 1.1,Ni余量。
1.2 BP神经网络建模
目前发展的神经网络理论技术较多,但性能比较优良的是BP神经网络。该神经网络是一种多层前馈神经网络,其主要特点是信号前向传递,误差反向传播。本文应用MATLAB对凝固组织与冷却速率的关系构建了BP神经网络,其工作原理包含以下步骤:
(1)网络初始化
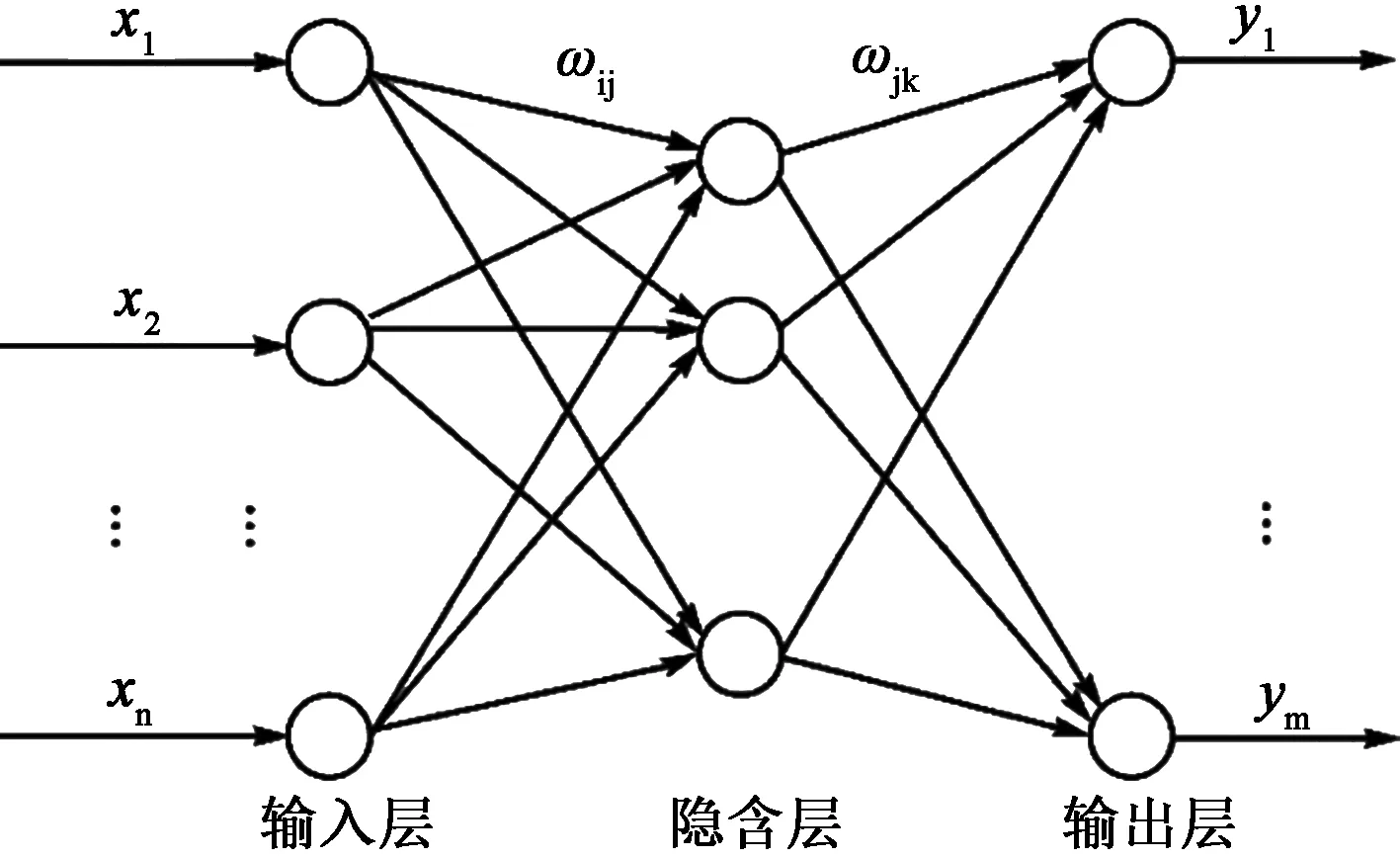
图1 BP神经网络拓扑结构图Figure 1 Topological structure diagram ofBP neural network
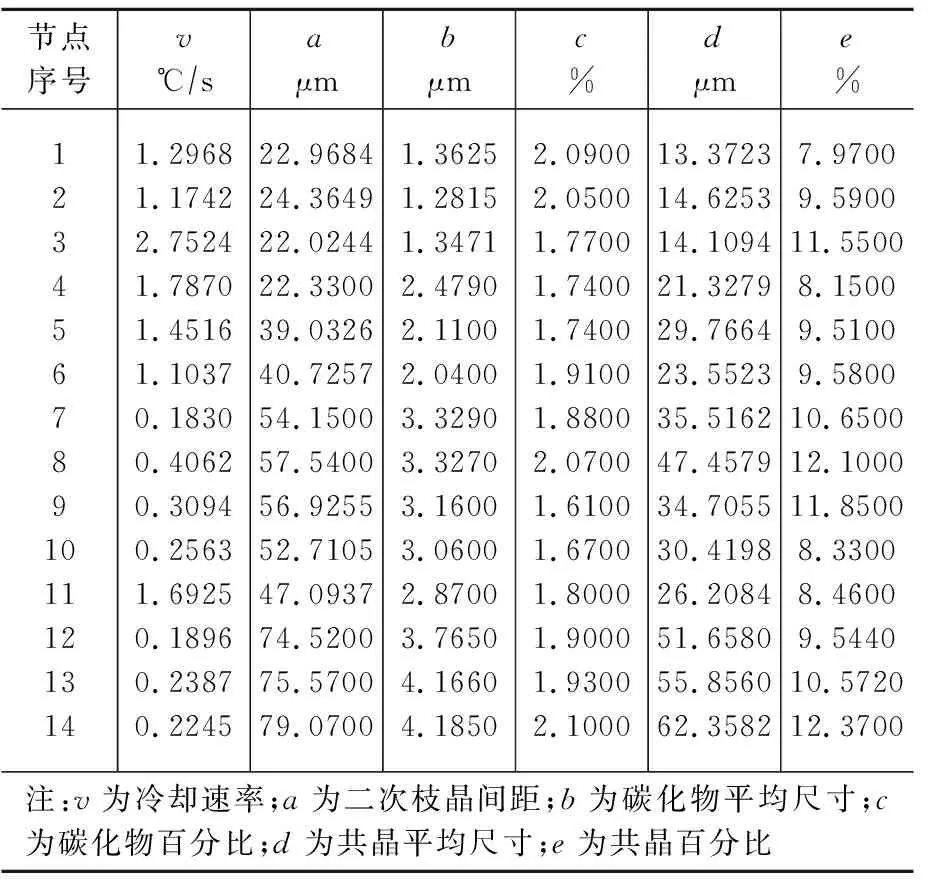
表1 神经网络训练数据组Table 1 Neural network training data set
(2)网络训练
通过对大量实验数据的自我学习和自我调整,最终建立凝固组织与冷却速率的非线性关联。训练网络需要大量的实验数据,笔者在燃机叶片上选取了17个位置点,逐一观测微观组织并借用ProCAST计算了相应位置冷却速率。其中14个位置点作为网络训练的数据样本,其凝固组织及冷却速率数据如表1所示。
(3)网络验证
网络训练完成后,为了验证其有效性。本文选取了叶片其他3个位置点数据进行网络预测。用预测值与实际值进行比较,验证偏差量。验证数据见表2。
2 结果与分析
2.1 凝固组织
对不同工艺参数浇注的标准试样进行力学性能测试,并解剖分析凝固组织,其测试结果如表3所示、微观组织如图2~4所示。
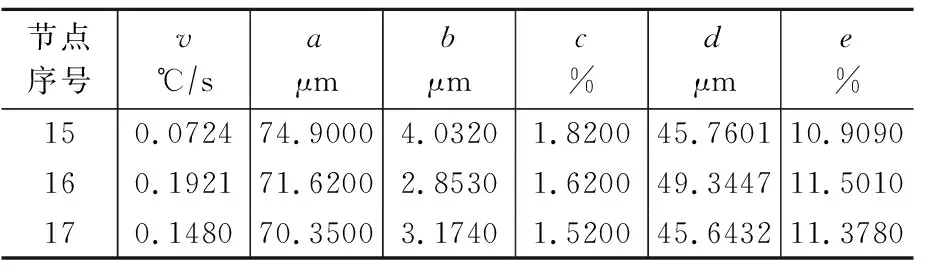
表2 神经网络验证数据组Table 2 Neural network validation data set
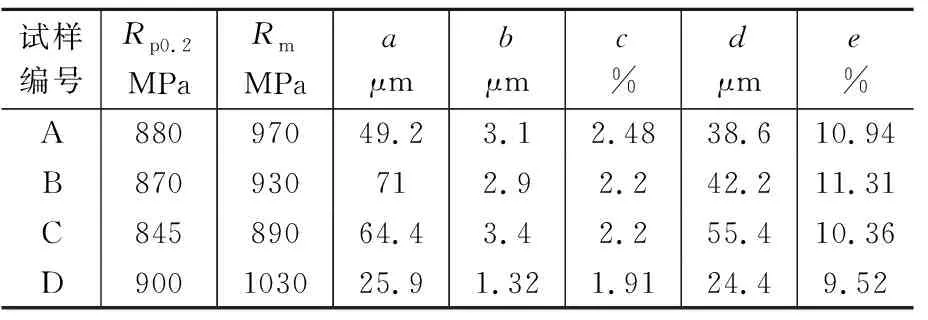
表3 室温强度及微观组织Table 3 Strength at room temperature andmicrostructure

图2 MM247合金碳化物形貌及尺寸(100×)Figure 2 Morphology and dimension ofMM247 alloy carbide(100×)
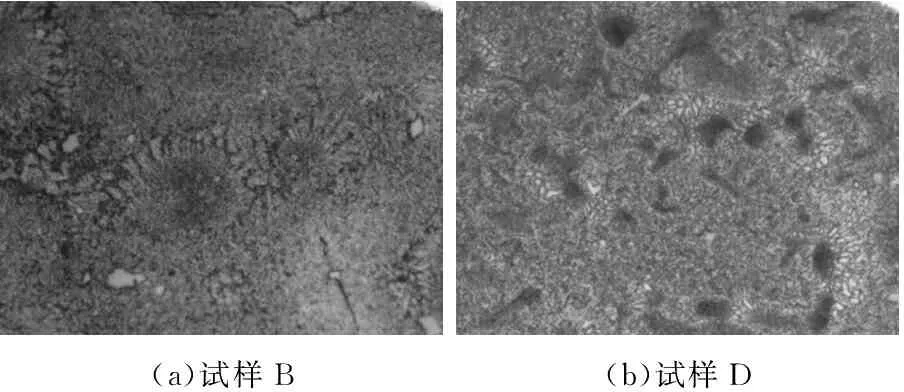
(a)试样B(b)试样D
从图2~4可以看出,相比试样B,试样D碳化物尺寸、共晶尺寸、二次枝晶间距均要明显小得多,说明增大冷却速率可以细化组织。同时,不同冷却速率下组织形貌差异也较大。如试样D碳化物呈现细长的草状,而试样B则呈现出球状。
由于组织上的差异,试样A~D具有明显不同的室温力学性能。其数值分布范围相差约60 MPa。而引起凝固组织及力学性能差异均可用冷却速率表征。因此,将冷却速率作为凝固组织与力学性能间的衡量参量具有重要意义,对性能的预测更是具备现实意义。

(a)试样D(50×)(b)试样B(100×)
2.2 神经网络训练及验证
根据神经网络建模原理,程序编制如下:
clear
A=load(‘1.txt’); %加载输入层数据
B=load(‘2.txt’); %加载输出层数据
P=A’;
T=B’;
NodeNum=5; %输入层单元数目
TypeNum=1; %输出层单元数目
Epochs=10000; %最多迭代次数
TF1=‘tansig’; %传递函数:正切sigmold函数
TF2=‘purelin’; %传递函数:线性函数
net=newff(minmax(P),[NodeNum TypeNum],{TF1 TF2},‘trainlm’); %建立训练网络
net.trainParam.epochs=Epochs; %网络训练参数:训练迭代步数
net.trainParam.goal=1e-5; %网络训练参数:误差控制精度
net.trainParam.show=200;
net.trainParam.time=inf; %网络训练参数:时间
[net,tr]=train(net,P,T); %开始训练
P1=load(‘3.txt’); %加载需预测输入层数据
P2=P1’;
T1=sim(net,P2); %预测
图5显示了神经网络迭代过程,结果显示,经过1400步的迭代,神经网络训练收敛,数据训练有效。为了验证神经网络的有效性,我们选取了3组数据作为验证,见表4。经验证,冷却速率预测值与实际值相差很小,说明神经网络训练成功,可以作为冷却速率预测的手段。
2.3 冷却速率与力学性能的关系
针对表3试样的凝固组织,本文以训练好的神经网络进行冷却速率的预测。预测数值见表5。
将冷却速率与力学性能进行拟合,得到如图6~7所示的关系。
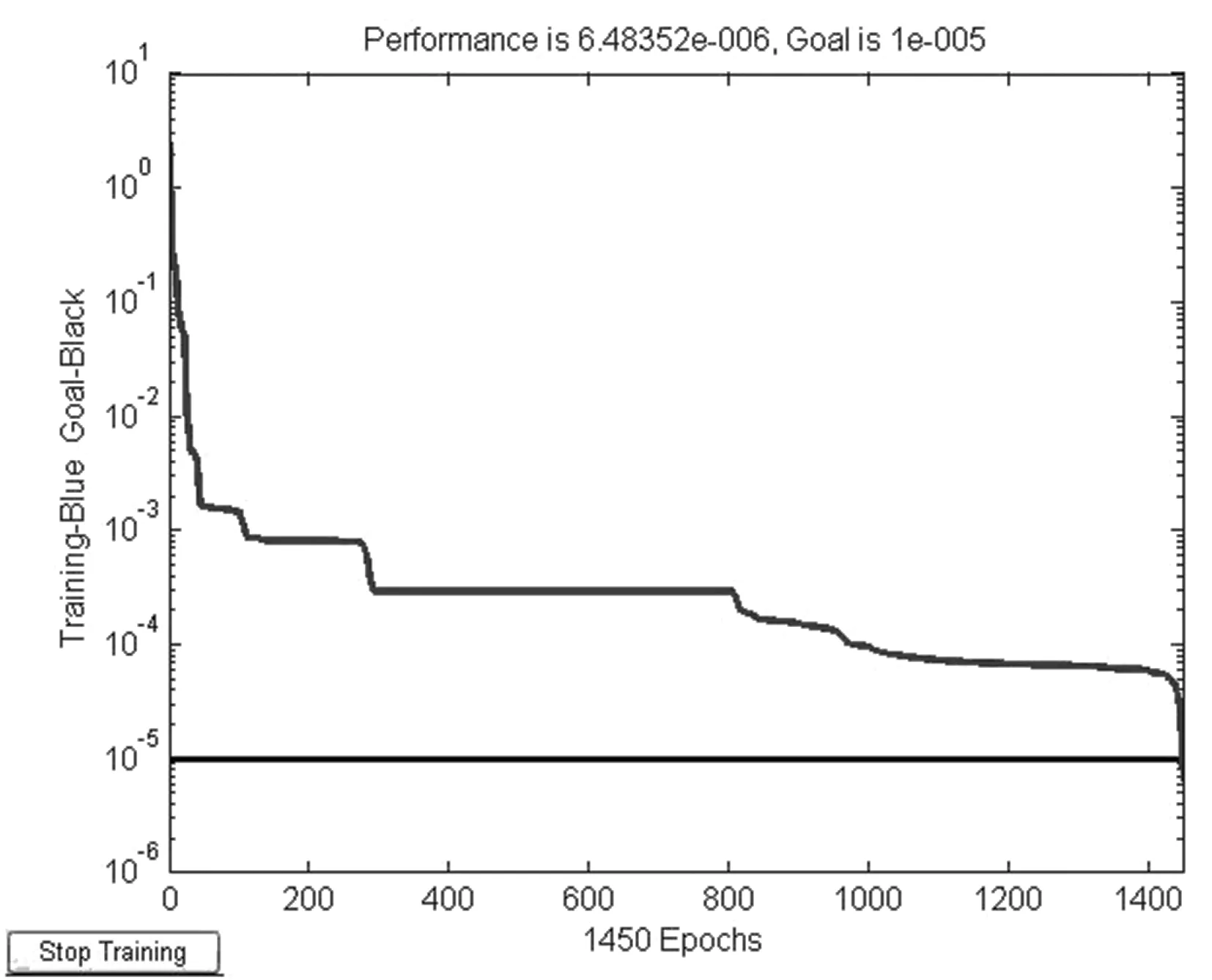
图5 神经网络训练过程迭代曲线Figure 5 The iterative curve of neural networktraining process
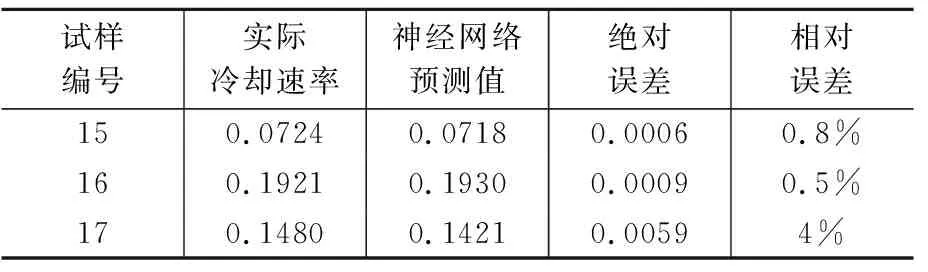
表4 神经网络验证Table 4 Neural network verification
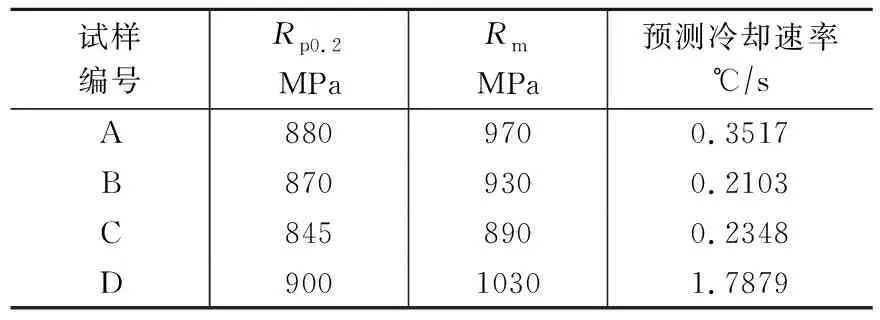
表5 神经网络预测值Table 5 Neural network predictive values
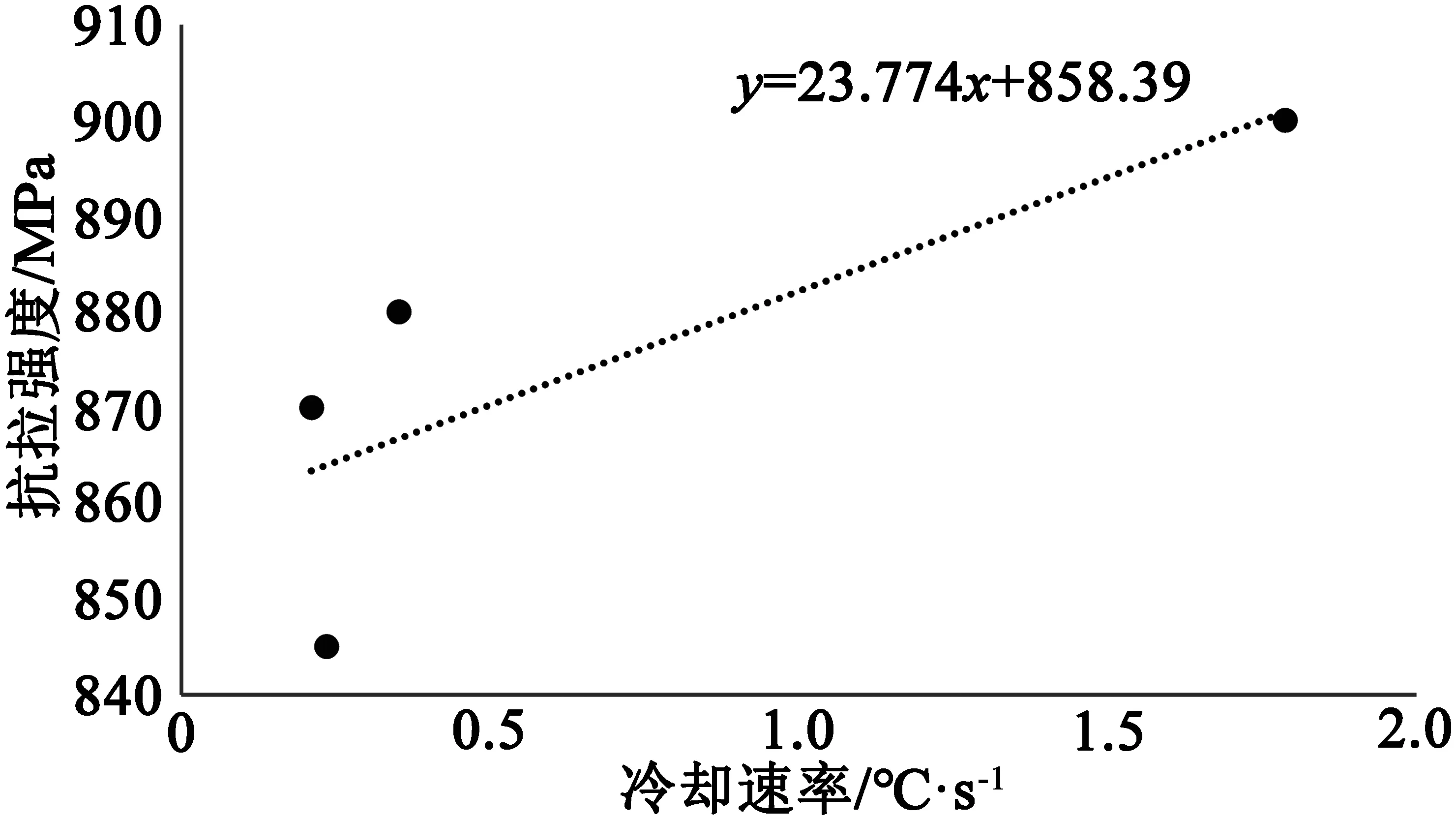
图6 屈服应力与冷却速率的关系Figure 6 Relationship between yield stress and cooling rate
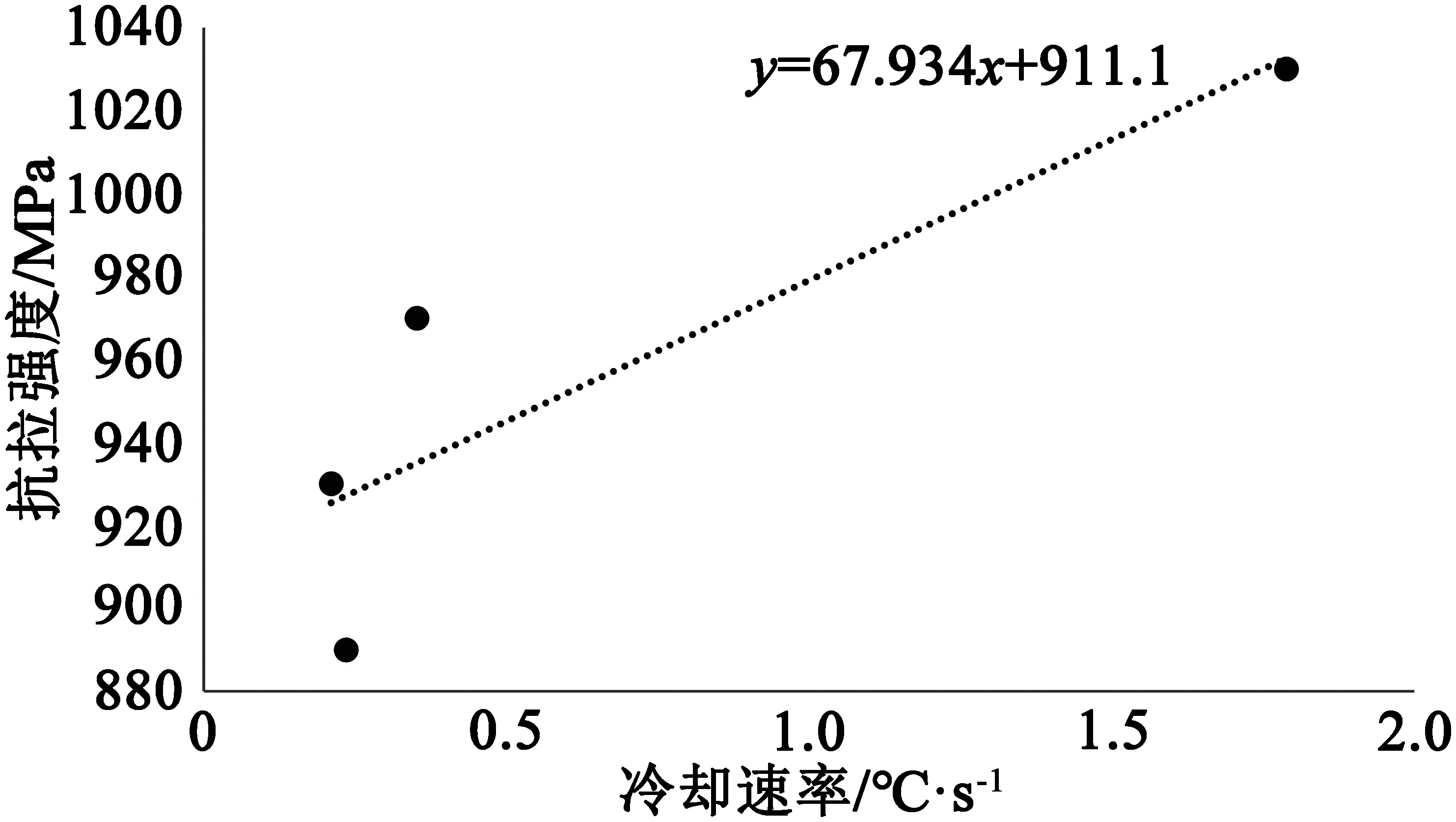
图7 抗拉强度与冷却速率的拟合关系Figure 7 Fitting relationship between tensile strength and cooling rate
从图中可以看出,当冷却速率增大时,屈服强度及抗拉强度明显增大。强度在不同冷却速率下可相差100 MPa,这主要是因为当冷却速率增大后,凝固组织明显细化,晶粒尺寸也变小,晶界强化作用明显加强。
通过上述拟合关系,可以在数值计算时求出各处冷却速率,以云图的形式显示各位置的强度,在工艺设计端给出强度预测,对工艺优化具有重要指导意义。
3 结论
本文采用ProCAST数值计算、显微组织观测及人工神经网络相结合的方式,研究了凝固组织与冷却速率及力学性能的关系,从而建立了冷却速率与力学性能的关系。主要得到以下结论:
(1)人工神经网络在建立复杂的凝固组织与冷却速率关系方面具有明显的优势;
(2)冷却速率作为重要的凝固参数,其严重影响着相组成及相含量;
(3)建立冷却速率与力学性能的关系,可以在工艺设计端准确预测不同位置的力学性能。

