永磁涡流联轴器结构参数的系列化分析研究

李延民，朱永建，毛松磊

（郑州大学机械工程学院，河南 郑州 450001）

1 引言

永磁涡流联轴器是一种非接触传动的联轴器，可实现主从动轴非接触传动，易于实现软启动、过载保护，有助于提高传动的可靠性[1]。国内对永磁涡流联轴器研究尚处于起步阶段，并且研究对象主要是针对特定传递功率的性能，尚未形成永磁联轴器的系列化研究。基于Ansoft 有限元分析[2]研究，采用等效磁路法[3-4]对永磁联轴器进行理论分析。运用Ansoft[5]软件对不同功率系列的关键影响参数（转速差、铜盘厚度、铝盘外形尺寸、永磁体径向尺寸、永磁体厚度）进行系列化分析研究，得到多个关键参数的变化规律，为以后其产业化设计提供设计依据。

2 结构与工作原理

永磁涡流联轴器由导体转子和永磁体转子组成，其中，导体转子包括：主动导磁盘和铜盘，永磁体转子包括从动导磁盘、铝盘、永磁体。永磁体盘由扇形永磁体嵌入于铝盘基体而构成，并且永磁体在铝盘上N、S 极交叉排列。基本结构，如图1 所示。

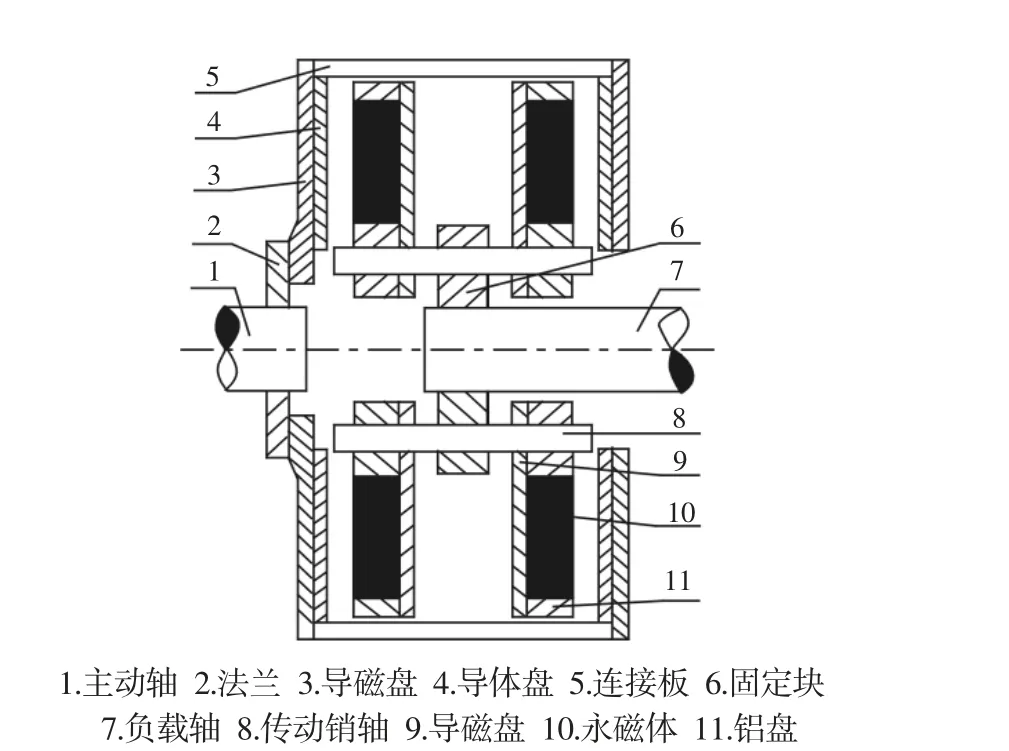
图1 永磁涡流联轴器的基本结构.Fig.1 Basic Structure of Permanent Magnet Eddy Current Coupling

工作原理：电机启动，带着主动轴高速旋转，连接着的铜盘因切割永磁体所产生的磁感线，在铜盘表面形成等效涡电流，涡电流会产生反感磁场，反感磁场与原磁场相互作用实现转矩的传递，带动从动轴转动，实现转矩速的传递。

3 转矩计算的数学模型

永磁涡流联轴器是左右对称的结构，仿真分析时可取单侧进行分析，转矩只需达到一半即可。与永磁涡流联轴器相匹配电机功率以及对应的额定转矩和相应的单侧转矩，如表1 所示。

表1 功率和转矩对应关系Tab.1 Power and Torque Correspond

转矩计算：运用等效磁阻法与楞次定律和安培定律进行转矩的计算。等效磁阻法就把空间不均匀分布的磁场等效的转化成多段磁路，如图2 所示。从而近似认为在每段磁路中磁通沿截面和长度均匀分布，将磁场的计算转化为磁路的计算。

图2 等效磁阻示意图Fig.2 Schematic Diagram of Equivalent Magnetic Circuit

在图2 中，R0、Rδ、RCu依次为永磁体、气隙、导体盘的磁阻，每块永磁体所产生的等效磁动势FD为：

式中：hpm—永磁体的厚度；Hc—永磁体的矫顽力。对于给定的永磁体的外形和性能均为定值，因此上式中等效磁动势Fpm定值。

根据磁阻计算公式，得到永磁体、气隙、导体盘的磁阻R0、Rδ、RCu分别为下式所示：

式中：δg—气隙厚度；δCu—导体盘厚度；Spm—永磁体截面积；μ0—空气磁导率；Φ—磁通量；B—磁感应强度；E—感应电动势分别为：

式中：r1—永磁体的内径；r2—永磁体的外径。

根据电流传导路线，根据式（8）计算出相应路径电阻R：

式中：ρ—铜盘电阻率；Lp—等效电流所做过的路程；S—横截面积大小。因此铜盘中单个涡电流为：

由于永磁体N、S 交错排列，因此铜盘上相邻的涡流方向相反。所以的铜盘区域形成的电流为自身电流两倍：

由安培定律可得电流路径上dl 的安培力dF：

单块永磁体所对应转矩的大小为T1为：

式中：B—永磁体的强度；I—铜盘涡流的大小；R—永磁体的径向长度。则总转矩为：

4 仿真模型的建立与研究

仿真模型基本结构[6]，如图3 所示。

图3 永磁涡流联轴器仿真模型Fig.3 Simulation Model of Permanent Magnet Eddy Current Coupling

进行系列化参数研究时，仿真过程中设定的常参数，如表2所示。

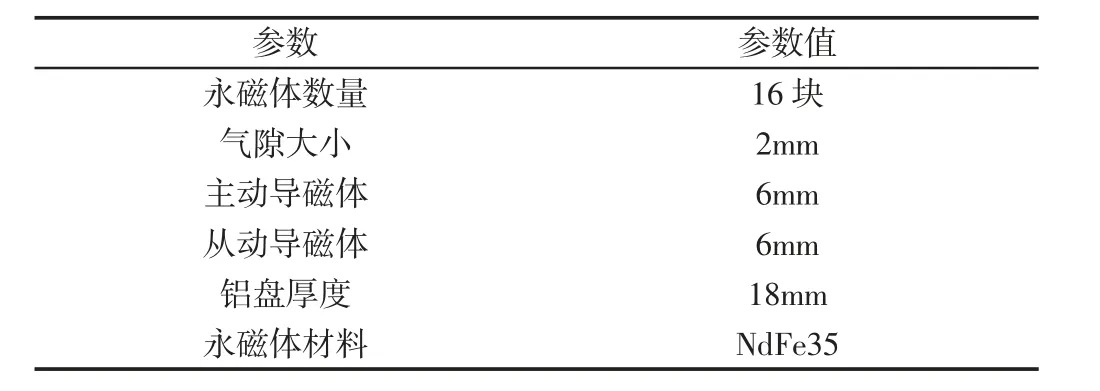
表2 分析模型基本参数Tab.2 The Basic Parameters of the Analysis Model

下面对影响永磁涡流联轴器的主要参数进行分析。

4.1 转速差

转速差直接影响着传递的效率。通过仿真得到不同功率输出转矩与轴向力随转速差变化的曲线，如图4、图5 所示。

图4 转速差与转矩的对应关系Fig.4 The Corresponding Relation Between the Relative Speed and the Torque

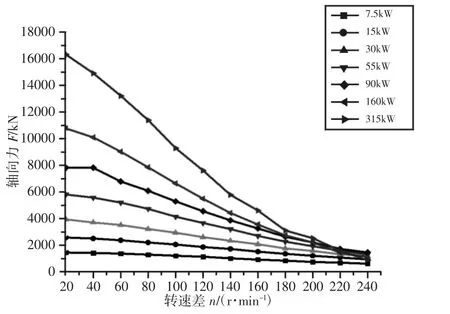
图5 转速差与轴向力的对应关系Fig.5 The Corresponding Relation Between the Relative Speed and the Axial Force

由图4 可知，随着转速差的增加，转矩均呈现先上升后下降的趋势。这是由于转速差和转矩成正比，随着转速差增加，转矩亦增加。当转矩达到峰值，增加转速差，铜盘的涡流损耗也增加，因此转速差达到峰值后，持续增加转速差转矩会减小。

根据图4，不同功率对应的曲线变化趋势大致相同，因此在满足正常工作所需输出转矩的前提下，不同功率的转速差均可在（80～100）r/min 范围内选取。

4.2 铜盘厚度

通过仿真，转矩和轴向力随着厚度的变化趋势，如图6、图7所示。

图6 铜盘厚度与转矩的对应关系Fig.6 The Corresponding Relation Between the Thickness of Copper Disk and the Torque

图7 铜盘厚度与轴向力的对应关系Fig.7 The Corresponding Relation Between the Thickness of Copper Disk and the Axial Force

由图6 可知，随着铜盘厚度的增加，转矩随之增加，当铜盘达到一定厚度后呈现下降趋势。这是由于随着铜盘厚度增加，相当于增加铜盘形成涡电流横截面积，其对应的电阻值减小，涡电流增加，感应磁场也增大，因此转矩增加。铜盘厚度持续增加，由于集肤效应，电阻值不再减小，但增加了永磁体与导磁体之间的厚度，漏磁也增加。根据图6，不同功率对应的曲线变化趋势大致相同，因此在满足正常工作所需输出转矩的前提下，不同功率联轴器对应的铜盘的厚度均可在（4～8）mm 之间选取。

4.3 联轴器的外形尺寸

永磁涡流联轴器的外形尺寸包括主、动导磁体、铜盘、铝盘的外形尺寸。不同功率的电机轴直径、轴心高，以及选取联轴器的内径，如表3 所示。上表为基础参数，在外径小于轴心高的基础上进行仿真分析。为直观分析多功率永磁涡流联轴器中外形尺寸的变化规律，取联轴器的径向有效尺寸（即联轴器的外径减去内径得到的尺寸）作为横坐标，得到联轴器外形尺寸对转矩和轴向力曲线，如图8、图9 所示。

表3 不同功率永磁涡流联轴器的内径Tab.3 Internal Diameter of Different Power Permanent Magnetic Eddy Current Coupling

图8 转矩和外形尺寸关系Fig.8 The Corresponding Relation Between the Boundary Dimension and the Torque

图9 轴向力与外形尺寸关系Fig.9 The Corresponding Relation Between the Boundary Dimension and the Axial Force

由图8 可知，永磁联轴器外形尺寸增加，转矩亦增加。其外形尺寸对整体结构与转矩都有较大影响。在满足安装空间、刚度、转矩、轴向力的前提下联轴器的外形尺寸可以适当大一些。通过仿真所选取的联轴器径向有效尺寸，如表4 所示。

3.投资公司需要定期召开风险预警会议，并不断培养对应的综合性风控人才，构建独立的风控机构。通过薪酬、待遇、人文尊重和企业关怀的角度着手吸引并培养专业高效的风控人员，将各部分掌握的相关信息共享讨论，营造公司整体的风控氛围，为投资公司的财务管理长效发展以及公司的高效运营奠定坚实基础。

表4 不同功率永磁涡流联轴器对应的铝盘尺寸Tab.4 The Corresponding Aluminum Plate Size of Different Power Permanent Magnetic Eddy Current Couplings

多功率永磁涡流联轴器随着联轴器的有效径向长度变化曲线，如图10 所示。

图10 功率与联轴器有效径向尺寸关系曲线Fig.10 The Relation Curve of the Effective Radial Dimension of the Aluminum Disk of the Power

通过MATLAB 线性拟合，得到方程y=0.2408x+91.87，其中确定系数R-square 为0.9893，R-square 正常取值范围在［0，1］之间，其值越接近1，表明方程变量对y 解释能力越强，数据拟合性越好。因此联轴器径向有效长度的变化曲线可近似看做一条线性变化的直线。

4.4 永磁体外形尺寸

根据文献[7]永磁涡流联轴器最优占空比在（75～80）%之间，既能满足转矩需求又能使永磁材料得到最大利用。根据计算所选取七个功率当永磁体数量均为16 块可保证在最优占空比范围内。根据电机轴的内径，选取的永磁体内径，如表5 所示。

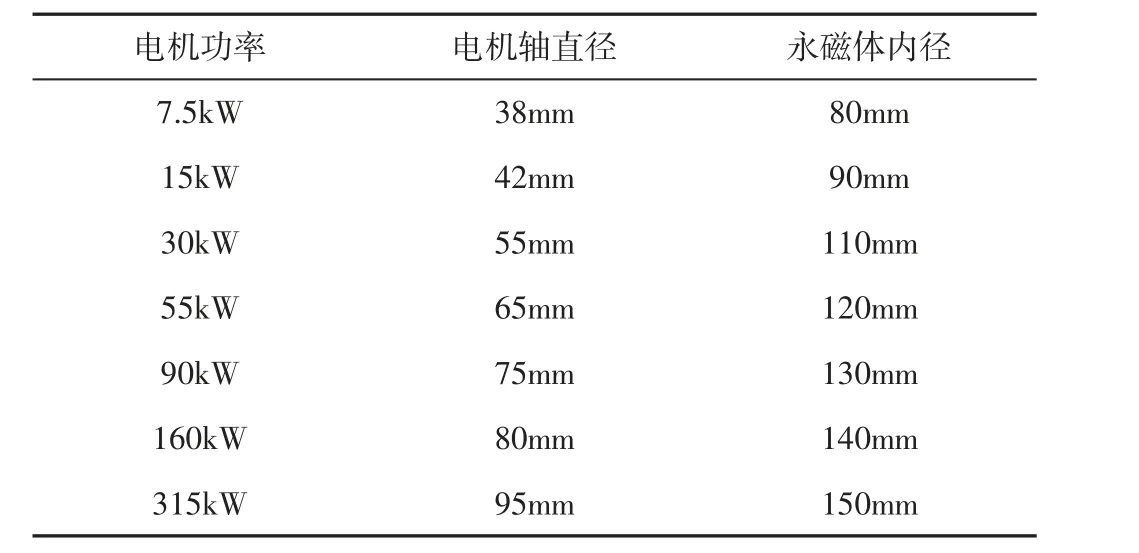
表5 不同功率永磁涡流联轴器的永磁体内径Tab.5 Permanent Magnet Internal Diameter of Different Power Permanent Magnetic Eddy Current Coupling

为直观表明永磁涡流联轴器永磁体径向长度变化规律，横坐标取永磁体径向有效长度进行研究，如图11、图12 所示。

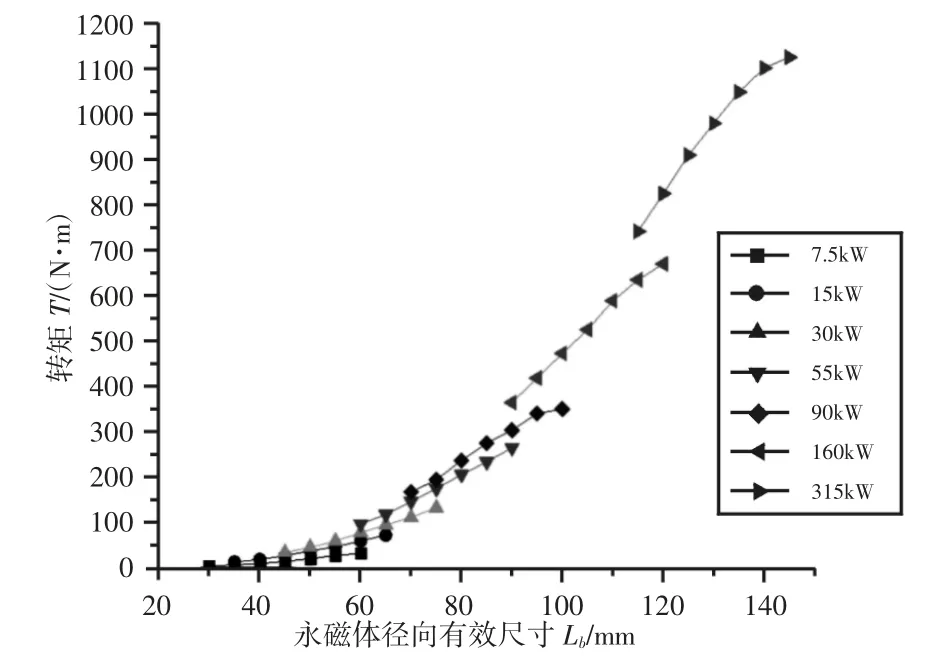
图11 转矩和永磁体径向有效长度关系Fig.11 The Corresponding Relation Between the Effective Radial Length of Permanent Magnet and the Torque

图12 轴向力和永磁体径向有效长度关系Fig.12 The Corresponding Relation Between the Effective Radial Length of Permanent Magnet and the Axial Force

从图11 可知不同功率的永磁联轴器，转矩和轴向力均随着永磁体的径向长度的增加而增大。永磁体价格昂贵，在满足传递转矩要求时，永磁体的外径应取较小值。由仿真所选取的不同功率对应的永磁体有效长度，如表6 所示。

表6 不同功率永磁涡流联轴器对应的永磁体尺寸Tab.6 Permanent Magnet Size for Different Power Permanent Magnetic Eddy Current Couplings

多功率永磁涡流联轴器随着永磁体的径向有效尺寸变化曲线，如图13 所示。

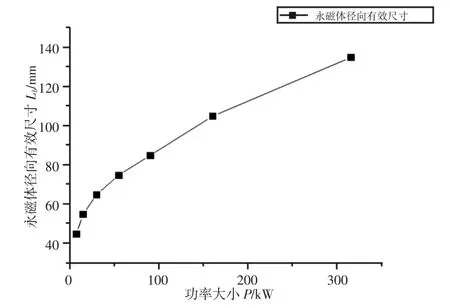
图13 功率与永磁径向有效长度关系曲线Fig.13 The Relation Curve Between the Power and the Effective Radial Length of Permanent Magnet

4.5 永磁体的厚度

在保证其他参数不变的情况下，改变不同功率永磁涡流联轴器下的永磁体的厚度，得到永磁体厚度与转矩和轴向力的变化曲线，如图14、图15 所示。

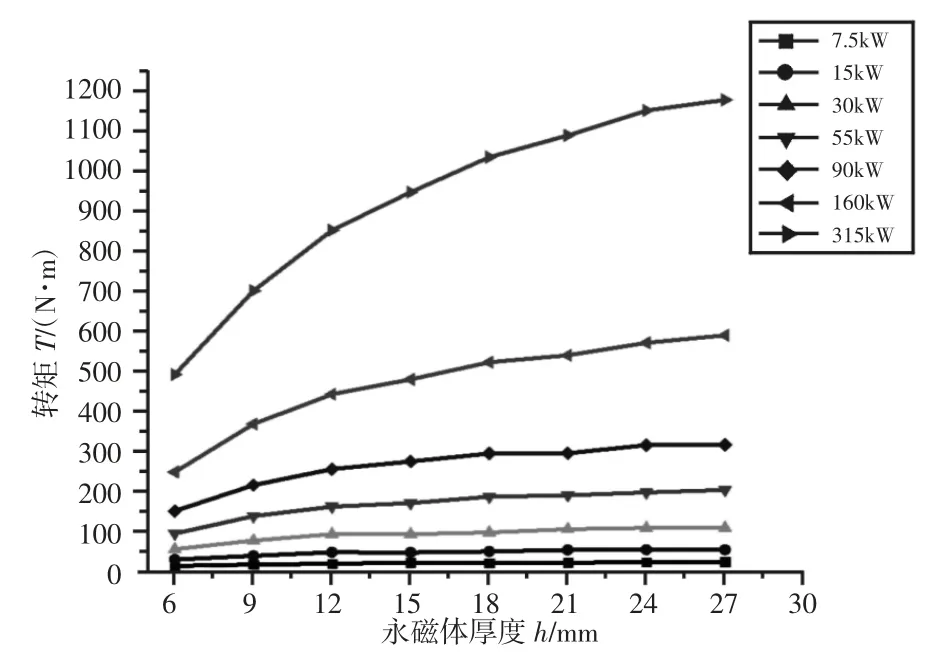
图14 转矩与永磁体厚度的关系Fig.14 The Corresponding Relation Between the Thickness of Permanent Magnet and the Torque

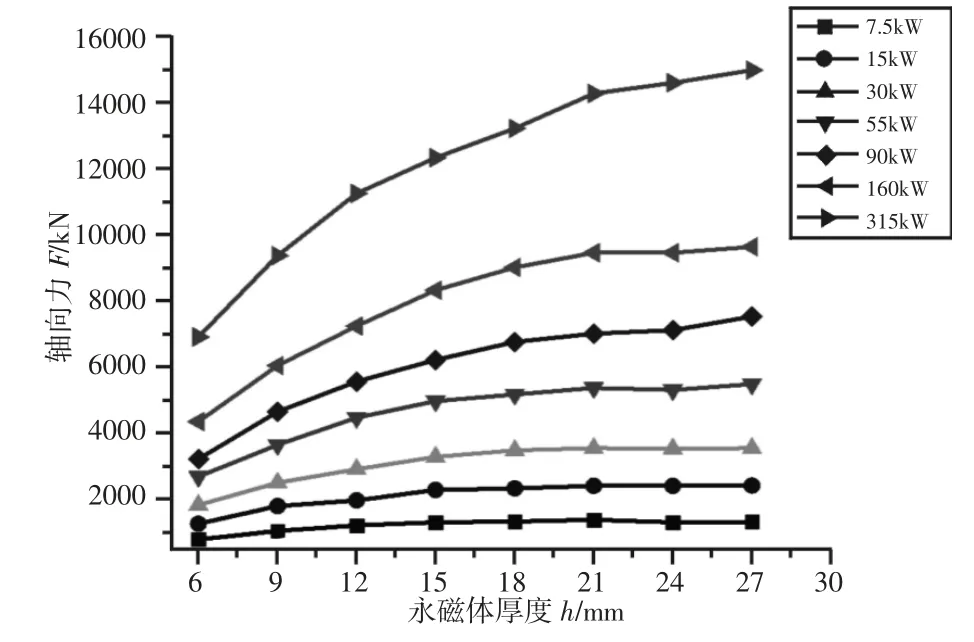
图15 轴向力与永磁体厚度的关系Fig.15 The Corresponding Relation Between the Thickness of Permanent Magnet and the Axial Force

由图14 可知，转矩与永磁体厚度成正比关系，但是斜率逐渐变小。这是由于随着永磁体的厚度增加，永磁体所产生的磁电动势变大，气隙磁密度变大，传递的转矩就变大。随着永磁体厚度持续增加，磁阻也相应增加，当厚度增大到一定值后，磁阻的增加抵消了磁电动势的增加。

根据图14，曲线变化趋势大致相同，因此在满足输出转矩前提下，不同功率永磁体厚度均可在（18～24）mm 范围内选取。

5 结论

针对不同功率的永磁涡流联轴器的五个关键参数进行系列化分析研究，可以得出以下结论：

（1）不同功率下的永磁联轴器转速差在（80～100）r/min 范围内选取时，均能满足输出转矩的要求。

（2）不同功率的永磁涡流联轴器，铜盘厚度的对转矩传递影响大致相同，因此多功率对应的联轴器的铜盘厚度均可选取在（6～8）mm 范围内选取。

（3）基于仿真分析得到最优尺寸，通过MATLAB 线性拟合，多功率永磁涡流联轴器的铝盘有效径向尺寸的变化规律曲线可以近似看做一条线性相关的变化直线。

（4）基于仿真分析得到最优尺寸，通过MATLAB 二次曲线拟合，多功率永磁涡流联轴器的永磁体有效径向尺寸的变化规律曲线可以近似看做一条开口向下的抛物线。

（5）永磁体的厚度直接影响着转矩与轴向力，并且直接关系成本。由仿真分析可得，不同功率的功率永磁涡流联轴器对永磁体厚度要求大致相同，均可在在（18～24）mm 范围内选取。