灰色模型在路基沉降预测中的研究及应用
张满想, 赵健, 郭昕, 龙健
(长沙理工大学 交通运输工程学院, 湖南 长沙 410114)
灰色预测理论是路基变形监测分析与预报理论中的重要组成部分,已广泛应用于各种工程变形监测预测。实际应用中,国内外学者提出了不少的优化方法来提高模型的精度,并指出:GM(1,1)、Verhulst分别适宜短期和中长期预测。但在实际操作时发现,灰色理论中“尽可能多地引入确定的实测数据”并不一定会提高模型的预测精度且实际操作中“尽可能的多”具体指几组数据也无明确界定,同时两种模型的适用时间并无明确的界限,这就为实际操作带来了困扰。
该文针对实际应用中遇到的上述问题,以湖南益马高速公路实测路基沉降数据为研究对象,分析两种模型下该组数据的最佳维度以及模型的适用时间;最佳维度的研究既能减少运算工作量同时也能提高两种预测模型的预测精度;模型的适用时间研究会明确两种模型的适用范围,进而更好地指导沉降预测工作。
1 工程概况
益马高速公路(益阳至马迹塘高速公路)第3合同段K25+700~K25+810路段全长110 m,属半填半挖路段,一级坡率为1∶1.75,二级坡率为1∶1.5,填方侧原位置为软土地基,软土主要为塑状黏性土,厚度一般<3.0 mm。沿线属亚热带季风湿润性气候,水系较发育,所经地域降雨充沛,地质主要由变质石英砂岩、砂质板和石英砂岩组成。其路基横断面示意图如图1所示。
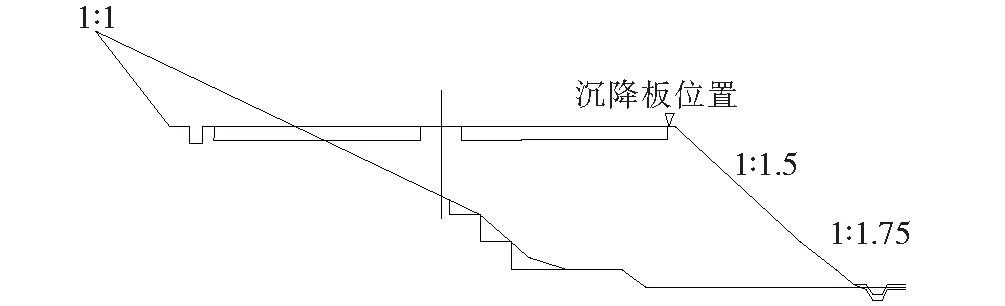
图1 路基横断面示意图
为保证车辆能够安全行驶于该试验段,同时了解路基沉降的变化情况,在试验段临近坡体位置处设置观测点进行路基沉降监测(图1)。监测频率为每个月不少于2次,并于2017年3月7日开始第1次监测。其路基沉降速率如图2所示。
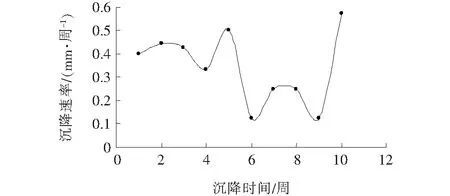
图2 路基沉降速率图
由图2可知:益马高速公路第3合同段K25+700~K25+810路基沉降速率大多数为0.6 mm/周以下,路基处于稳定状态,但最后一周的路基沉降速率是前一次监测沉降速率的3~4倍,路基沉降速率发生突变;为保证路基后期的稳定状态,需要对该路基进行长时间的监测,详细掌握该路基沉降变化状况。
2 灰色模型预测方法及效果检验
2.1 灰色模型预测方法
灰色模型一般是通过时间序列在时间数据平面上的连续曲线或逼近曲线与时间轴所围成的区域为基础,利用系统部分已知信息,以微分拟合而建成的模型,两种预测模型的表现形式一般为指数形式和S形曲线,灰色模型计算过程如下:
设非负离散数据序列:S(0)={s(0)(1),s(0)(2),…,s(0)(n)},对S(0)进行一次累加得到:S(1)={s(1)(1),s(1)(2),…,s(1)(n)},灰色预测模型的微分方程如式(1)、(2)所示。
灰色GM(1,1)预测模型的微分方程为:
(1)
灰色Verhulst预测模型的微分方程为:
(2)
(3)
则灰色GM(1,1)预测模型的时间响应序列为:
(4)
则灰色Verhulst预测模型的时间响应序列为:
(5)
运用上述灰色模型预测方法对路基沉降的实测值进行处理,达到研究维度和确定两种模型预测时间的目的。具体步骤如下:
(1) 灰色模型计算
采用两种灰色模型对实测数据进行运算,计算得出不同维度的拟合公式。
(2) 最佳维度分析
对比不同维度拟合公式的关联度和拟合误差,初步确定最佳维度;通过选取的最佳维度进行两种模型的预测运算,根据其预测效果判定最佳维度的合理性。
(3) 模型的预测时间分析
通过步骤(2)确定模型的最佳维度,在此基础上计算模型长时间的预测值,通过对比确定模型的预测时长。
2.2 模型效果检验
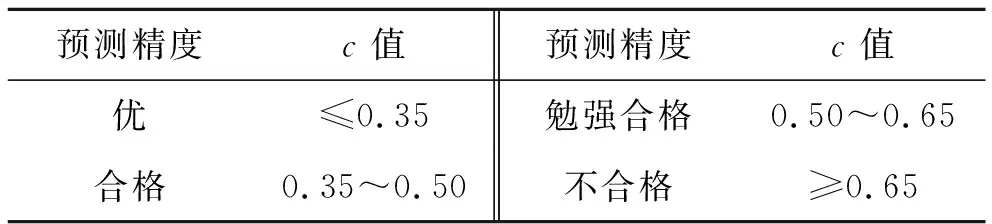
后验差检验法是一种求残差分布统计特征的计算方法。计算出的c值为残差标准差与观测值标准差之比,用于判定两者变异程度大小;变异程度,即最大和最小的观测值之间的差距,若变异程度越接近,则预测值与观测值的拟合相似程度越高,预测方程越精确。后验差检验步骤如下:
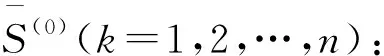
(6)

(7)
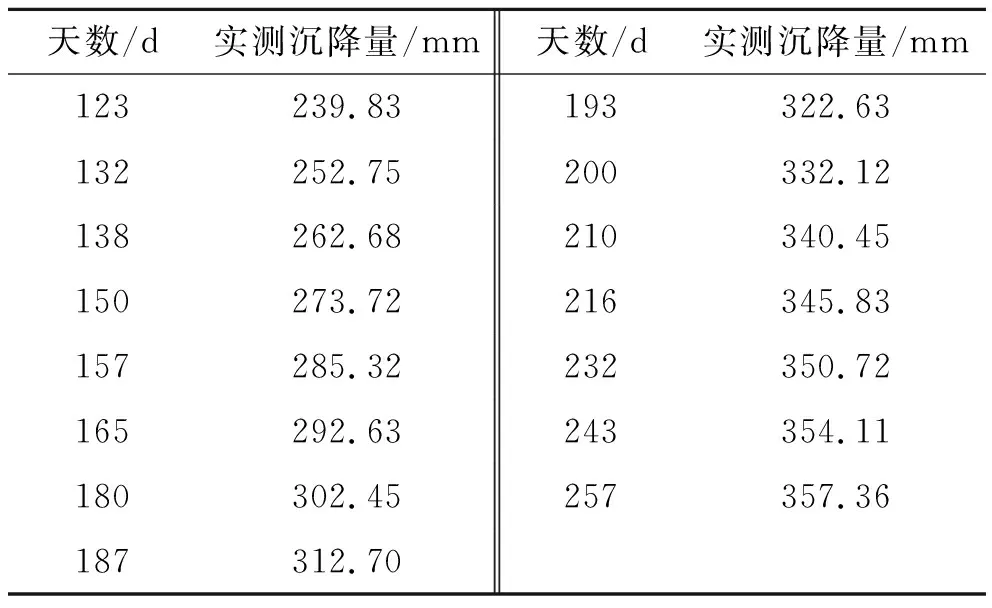
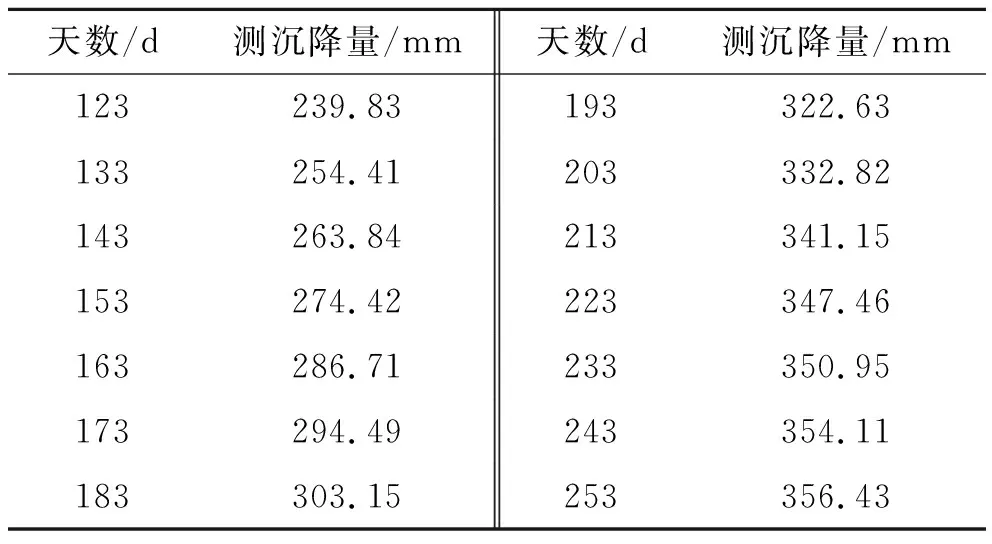
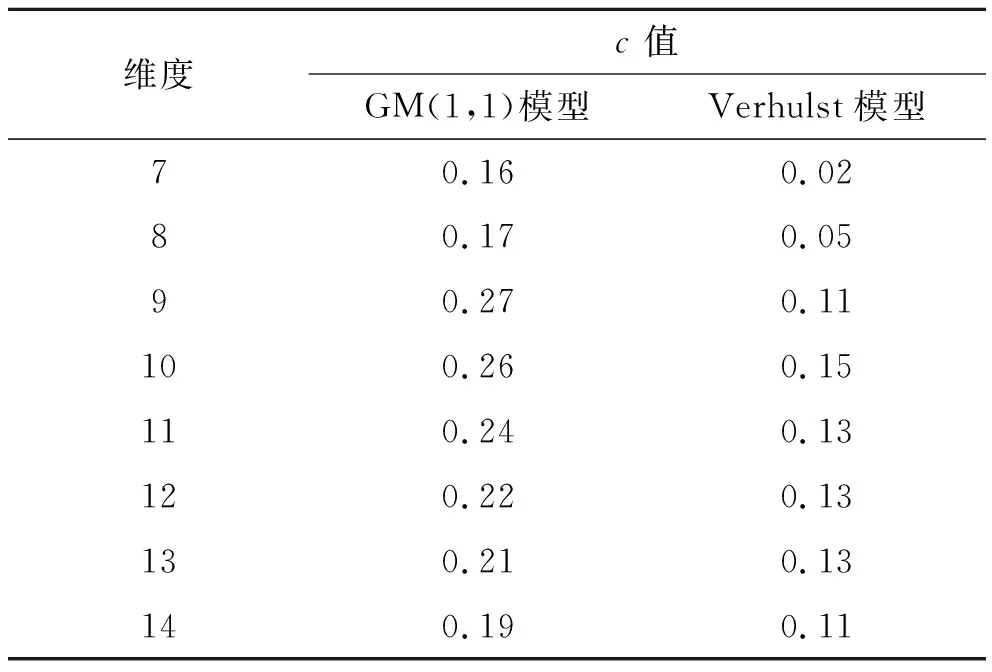
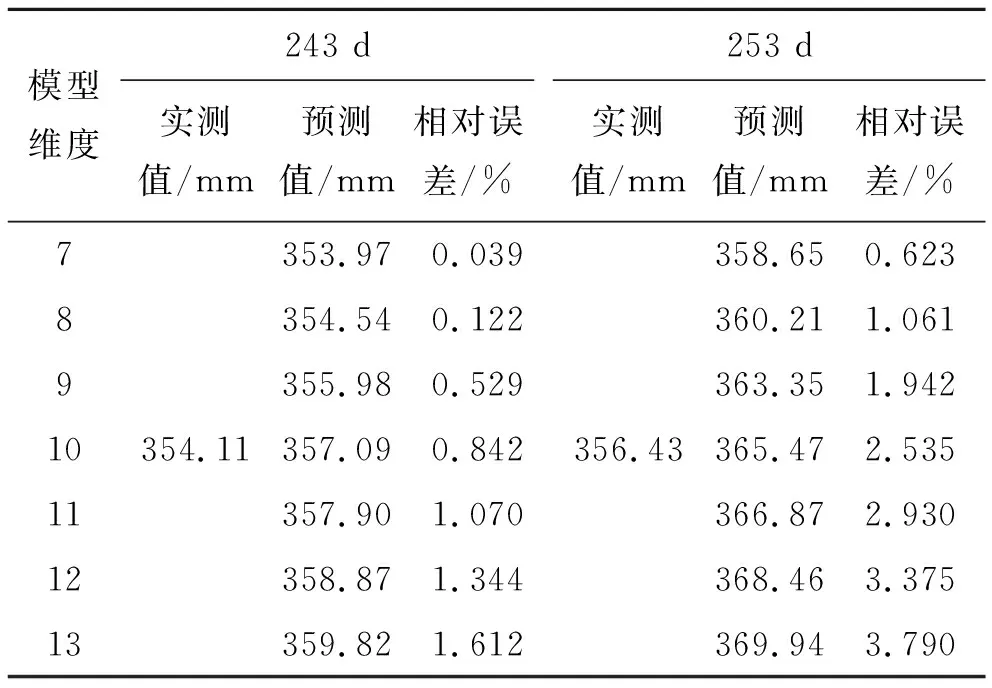
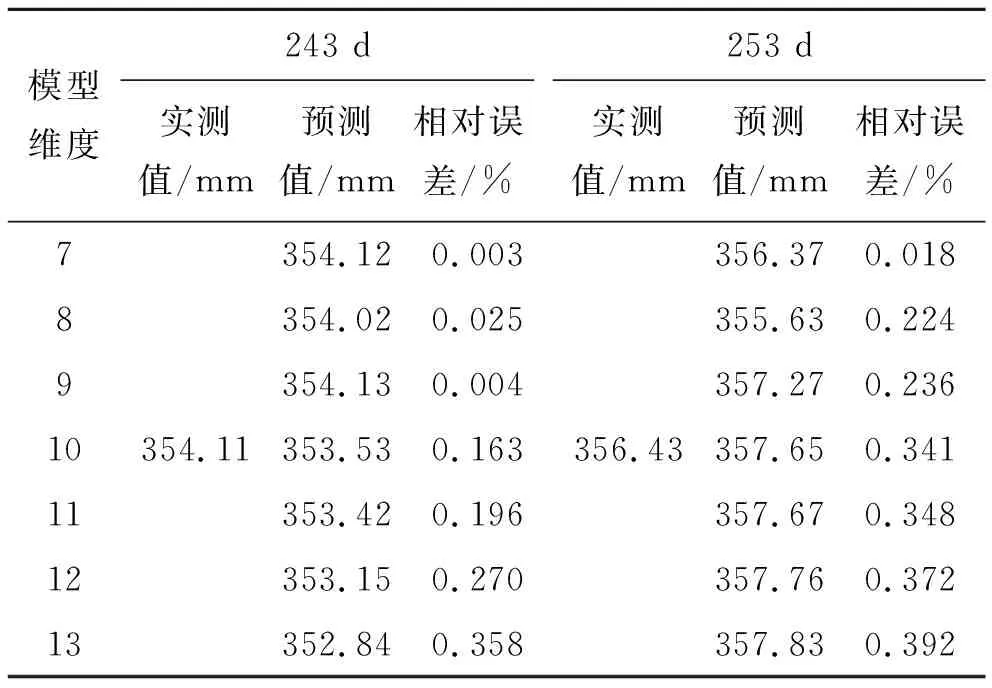
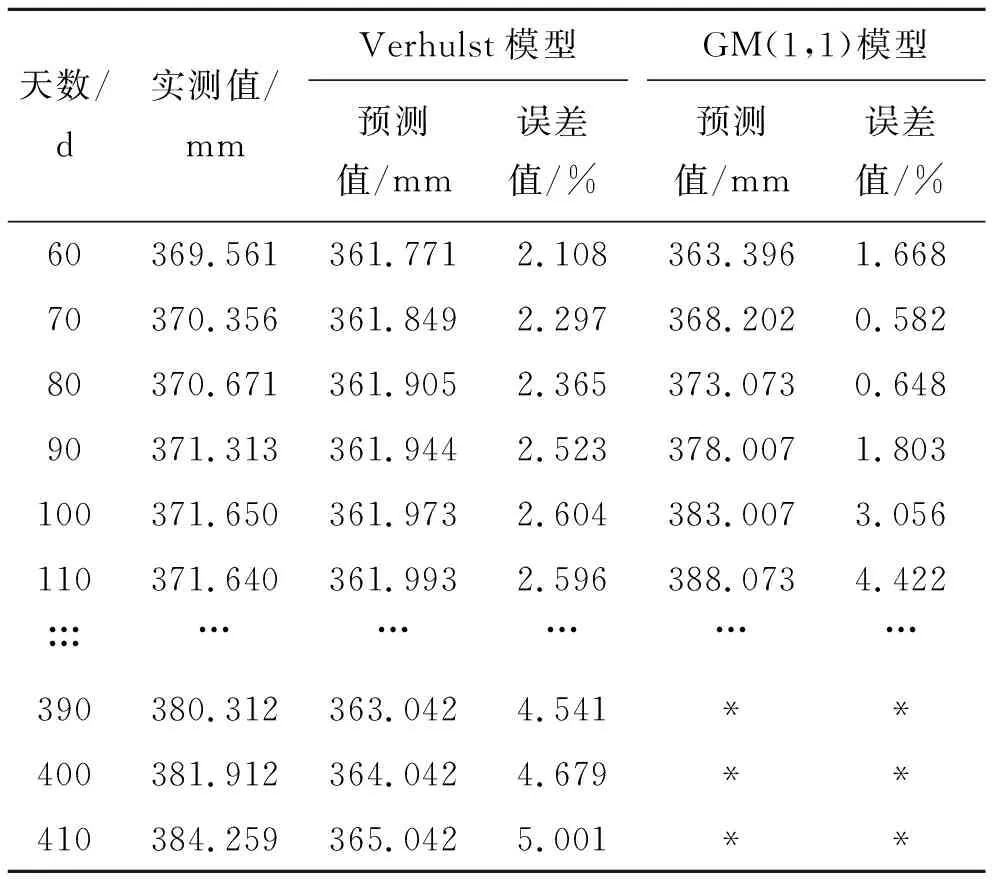
式中:n′为q(k)中非零残差的个数,n′ (8) (9) (4) 计算后验差比值c: (10) (5) 根据计算结果,对照表1中的指标,评定模型的精度等级。 表1 模型预估精度等级评定标准 取该观测点实测数据,进行最佳维度研究。该文以观测点的实测数据为依托,取123~257 d的实测数据,如表2所示。 由于现场实测的路基沉降数据是非等时距的,所以在建模之前要进行等时距的处理,利用拉格朗日插值定理计算等时距各天的沉降值(取两位小数),具体数值见表3。 表2 断面实测数据 表3 处理后的等时距各天沉降值 采用灰色GM(1,1)和灰色Verhulst模型对断面观测点监测数据进行建模分析,首先根据表3实测数据进行维度划分,按照监测数据的时效性,选择最临近监测时间的数据进行不同维度的模拟计算,通过精度检验,确定最佳维度。根据式(6)~(10)计算出c值,不同维度下的后验差检验结果如表4所示。 表4 后验差检验c值 由表4可知: (1) 通过后验差方法检验发现,GM(1,1)、Verhulst预测模型在7~14维度间的c值先增大后减小,同时c值都小于0.35,预测精度优;维度处于9时c值最大,7~9维度的c值变化速率要高于9~14维度c值的变化速率;同时发现,Verhulst预测模型的c值相比于GM(1,1)预测模型的c值较小,模型精度高于GM(1,1)模型。 (2) 灰色GM(1,1)、Verhulst模型不同维度方程在维度为7时c值最小,模型精度较高,同时维度计算工作量最小。因此选取7组数据进行方程拟合,工作量较小同时效果较好。 采用GM(1,1)和Verhulst模型分别对243、253 d的沉降值进行预测,结合表3中的监测数据确定模型的预测维度最大值为13,预测结果如表5、6所示。 表5 不同维度下GM(1,1)预测结果与实测结果对比 表6 不同维度下灰色Verhulst模型预测结果与实测结果对比 结合模型检验分类等级表对模型精度进行分析,按取值的大小,预测模型的精度等级可分为 一级(好)、二级(合格)、三级(勉强)和四级(不合格),取值标准见表7。 表7 模型精度检验等级分类 由表5、6可知: (1) GM(1,1)模型预测过程中随着维度的增加其预测精度都有所降低,拟合误差增大;而Verhulst模型在预测过程中精度会出现回升的现象,但整体来看该模型也是随着维度的增加其预测精度都有所降低,拟合误差增大;在维度为7~13时,两种模型都是维度为7时预测值精度最大,拟合误差最小。 (2) 从两种预测模型的精度对比可以看出:Verhulst预测模型的精度要高于灰色GM(1,1)模型;又因灰色GM(1,1)拟合公式为指数形式,与实际路基沉降情况不符合,同时由表5可知,在采用灰色模型GM(1,1)预测时会在未来一定时间内出现无效性数据。 根据上述最佳维度研究和预测效果检验可知:两种灰色模型选取维度7建模时,不仅还原方程c值较低,且预测值的误差相对于其他维度也较小。因此取维度7数据进行验证并讨论两种模型的预测停止时间;计算结果如表8所示。 表8 计算结果预测统计 GM(1,1)预测公式如下: (6) Verhulst模型预测公式如下: (7) 由表8可知: (1) GM(1,1)模型的表达式基本形式为指数函数,预测数值增加较快且当预测时间较长时,误差值增大速率也较快,在第5月时其误差值超过5%,因此GM(1,1)模型不宜对沉降进行4个月后的预测。 (2) Verhulst模型在预测路基沉降时,误差值逐渐增大,在第14月时其误差值超过5%,考虑其路基处治的安全性,因此Verhulst模型不宜对沉降进行14个月后的预测。 (3) 采用灰色Verhulst模型对益马高速公路路基沉降进行1年内的预测,预测结果表明:在1年内,路基的最大沉降速率为0.35 mm/周,路基保持稳定状态。 通过对益马高速公路典型路基断面实测数据进行拟合及预测计算,得到以下结论: (1) 针对益马高速公路路基断面的特点,运用GM(1,1)、Verhulst模型对该路基监测数据进行分析,结果表明:在维度为7时,拟合方程通过后验差检验c值最小,且预测值的相对误差最小。 (2) 灰色模型GM(1,1)适宜短期预测的时间是4个月内,而Verhulst模型适宜中长期预测的时间是14个月内,两种预测模型随着时间的延续,预测等级都会降低;同时采用灰色Verhulst模型对益马路基沉降进行1年后的预测,预测结果表明,在1年内,路基的最大沉降速率为0.35 mm/周,路基保持稳定状态。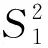
3 灰色理论模型计算
3.1 最佳维度研究
3.2 模型预测效果检验

4 预测时间研究
5 结论

