组合缺陷影响下衬砌结构受力特征分析

殷洪波，刘正初，郭永发

组合缺陷影响下衬砌结构受力特征分析

殷洪波，刘正初，郭永发

(中铁二院昆明勘察设计研究院有限责任公司，云南 昆明 650200)

以云南山区某2车道公路隧道为依托，建立基于围岩压力修正的荷载−结构模型。通过引入衬砌安全性影响系数，开展衬砌背后空洞和厚度不足组合缺陷影响下的衬砌受力特征分析。研究结果表明：衬砌厚度不足和背后空洞的存在会改变衬砌局部刚度及其与围岩的接触状态，从而引起衬砌内力重分布。衬砌缺陷的影响主要集中在缺陷处及其邻近部位，缺陷程度越大，衬砌受影响范围越大；缺陷影响范围内的衬砌轴力减小、弯矩增大，安全系数降低，恶化了结构受力状态。当拱顶存在组合缺陷时，衬砌安全性影响系数随着缺陷程度的增加基本呈线性增长，而当单侧或双侧拱腰存在组合缺陷时呈双线性增长规律。比较而言，背后空洞对结构安全性的影响更大；拱腰组合缺陷的影响大于拱顶部位，较小的组合缺陷就会对结构安全性造成较大影响。

山岭隧道；衬砌背后空洞；衬砌厚度不足；围岩压力修正；影响系数

近年来，随着我国公路、铁路进一步向西部地区延伸，运营隧道的总数量正以每年上千座、总里程正以每年上千公里的速度增加。截止2018年底，我国大陆运营公路隧道和铁路隧道总里程分别达到17 236 km和16 331 km[1]。在隧道建设快速发展的同时，隧道服役状况不甚理想，特别是早期修建的隧道，衬砌背后空洞、衬砌厚度不足等质量缺陷以及隧道渗漏水、衬砌开裂等病害问题较为严 重[2−5]。与衬砌开裂等病害不同，衬砌背后空洞、衬砌厚度不足等缺陷具有隐蔽性，但这些缺陷的存在及发展直接影响结构安全和耐久性，已引起国内外学者的广泛关注。为此，采用模型试验、数值计算和理论分析等方法开展了一系列工作，取得了较为丰富的研究成果[6−17]。如佘健等[6−8]开展了衬砌背后空洞、衬砌减薄影响下的衬砌结构变形规律、承载性能和裂损规律的模型试验。结果表明：背后空洞的存在易导致衬砌承载力不足，影响隧道受力状态；围岩条件越差，衬砌减薄引发的隧道病害程度越严重。DING等[9]通过背后空洞条件下钢筋混凝土衬砌承载性能的大比例尺模型试验，建立了考虑空洞影响下的衬砌承载力损失率公式。李彬等[10−13]采用数值分析方法，分析了衬砌减薄和脱空对衬砌安全系数的影响，给出了缺陷程度与结构最小安全系数之间的关系。叶艺超等[14]通过弹塑性有限元分析，研究了空洞尺寸、位置和深度对衬砌内力及围岩应力分布的影响，得到了空洞边缘易出现应力集中的结论。应国刚等[15]考虑到空洞附近范围的围岩应力重分布，提出了考虑空洞影响的修正荷载−结构模型，计算结果表明其与模型试验结果一致，可用于缺陷衬砌结构的安全性评价。聂子云等[16−17]采用数值计算和振动台模拟试验方法，开展了衬砌背后空洞条件下隧道地震响应研究，指出缺陷的存在会明显降低隧道结构的抗震性能。上述研究有助于认识空洞、衬砌厚度不足等缺陷影响下隧道力学行为。但已有研究多从定性角度分析[6−8, 14]，或虽采用定量分析，但建立的计算模型与实际情况有差异[10−12]。虽然文献[15]建立了修正荷载−结构模型，但文中仅考虑了拱顶空洞，对隧道质量缺陷的影响缺乏系统研究。另外，实践中发现衬砌背后空洞与衬砌厚度不足往往同时存在，但定量评价这种组合缺陷的影响还较少。鉴于此，本文建立基于荷载修正的计算模型，以云南山区某典型2车道公路隧道为例，并引入结构安全性影响系数，研究衬砌厚度不足和背后空洞组合缺陷下衬砌的内力分布、安全系数的变化规律，以期为缺陷评价提供参考依据。

1 围岩压力修正计算方法

荷载−结构法是衬砌结构计算与安全性评价的常用方法，但采用该方法计算衬砌背后存在空洞的情况时，不能简单去除空洞区域的围岩压力及约束。试验结果表明，空洞附近范围内围岩应力有明显集中现象[14−15]，因此，应对作用在空洞附近衬砌上的围岩压力进行修正。文献[15]提出空洞附近采用三角形面积等效的荷载修正模型，但该修正方法在空洞较大时应力集中效应偏大，鉴于此，本文结合开孔问题的应力集中现象，采用梯形面积等效修正荷载模型，如图1所示。

图1中，代表空洞的半径；表示无空洞缺陷时隧道竖向围岩压力；max为围岩压力的峰值；表示空洞存在时，围岩压力影响范围和空洞半径的比值；为围岩压力逐渐增大段与围岩压力影响范围的比例。此外，设定0为隧道最大开挖宽度的一半。根据空洞半径的大小，有如下3种情况：

当空洞半径时≤0/4，空洞区域荷载完全转移到了空洞两侧，此时围岩压力呈梯形分布，梯形底部宽度为，如图1(b)所示。由图中2阴影面积相等可得：

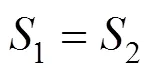
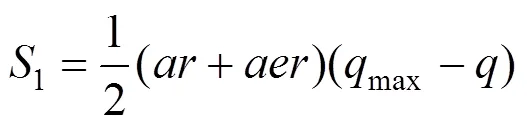
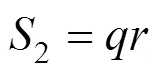
当空洞半径时0/4＜＜0/2，空洞区域荷载向空洞两侧转移，此时围岩压力呈梯形分布，但梯形底部宽度小于。同样，根据2阴影面积相等可得：

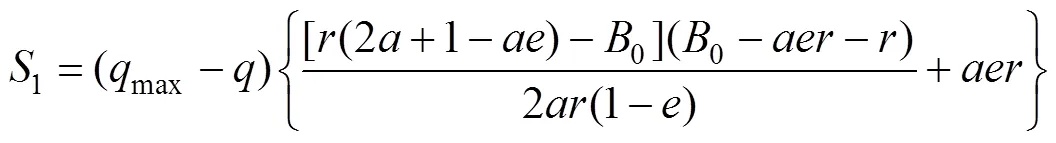
当空洞半径时≥0/2，空洞区域荷载完全转化为围岩压力峰值，此时围岩压力呈矩形分布，可得：

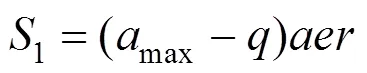
依据相关模型试验研究成果[15]，取和分别为3和1/3。由此得出max为：

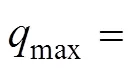
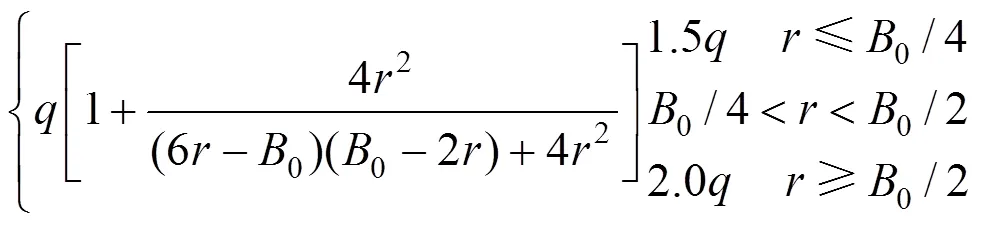
当确定空洞尺寸和隧道开挖宽度后，即可按照图1和式(6)进行围岩压力修正计算。当空洞位于拱腰时，其计算方法与此相同。

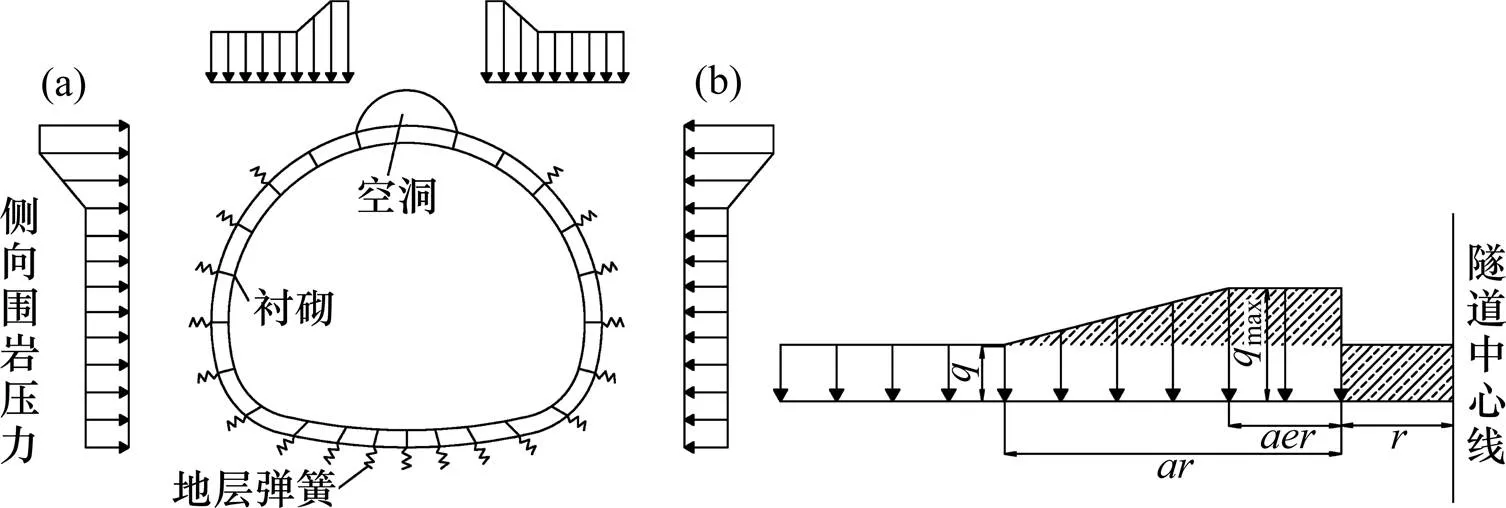
(a) 计算简图；(b) 围岩压力分布修正

2 组合缺陷计算模型

2.1 依托工程及计算参数

本文主要探讨含空洞和厚度不足组合缺陷衬砌的受力特征，为此，以云南山区某IV级围岩段2车道高速公路隧道为依托，隧道开挖跨度12.24 m，高9.57 m。二次衬砌采用厚40 cm的C30素混凝土衬砌。围岩及衬砌材料物理力学参数见表1。

表1 衬砌及围岩物理力学参数

计算时，隧道按深埋考虑。依据设计规范，计算得到竖向围岩压力=136.5 kN/m，水平向围岩压力=54.4 kN/m。参照《公路隧道设计细则》(JTG- TD70−2010)，围岩压力由初期支护和二次衬砌共同承担，Ⅳ级围岩可取二次衬砌荷载承载比例为30%，由此可得到无缺陷条件下作用在衬砌结构上的荷载。

2.2 计算工况

基于围岩压力修正计算方法和建立的缺陷衬砌计算模型，本次计算主要考虑衬砌拱顶和拱腰部位存在组合缺陷的情况，如图2所示，具体计算工况见表2。衬砌背后空洞范围用角度表示(见图2)。为简便，定义δ为衬砌减薄厚度比，其表达式为：

=/0(7)

式中：为衬砌减薄厚度；0为完好衬砌厚度。

为便于分析，表2中，衬砌背后空洞用符号“V”及其对应角度表示，减薄用符号“T”及其对应减薄比表示。如V30T0.125表示衬砌空洞30°且减薄比0.125的组合缺陷。

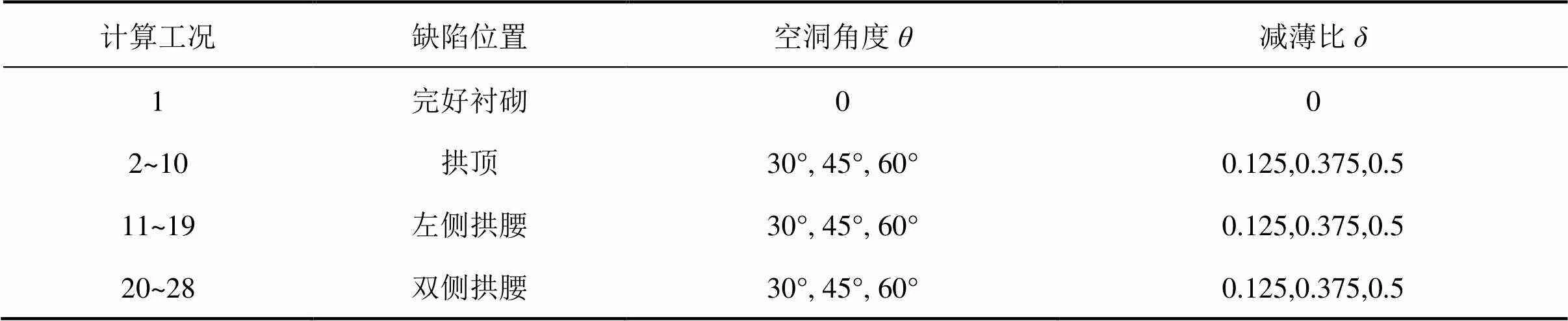
表2 计算工况

(a) 拱顶空洞+减薄；(b) 拱腰单空洞+减薄；(c) 拱腰双空洞+减薄

2.3 缺陷对衬砌安全性影响的评价方法

依据《公路隧道设计规范》[18]来计算截面的安全系数。为了更直观地表达组合缺陷对整个衬砌结构安全性的影响，引入结构安全性影响系数，可表示为：

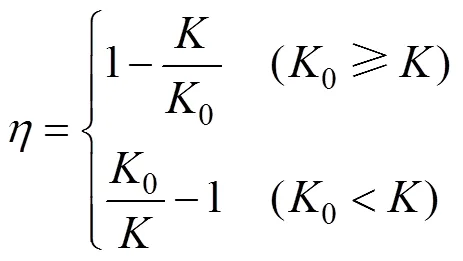
式中：为衬砌安全性影响系数，其值为正表示对结构安全性产生不利影响，为负则表示对结构安全性产生有利影响。为缺陷衬砌的最小安全系数；0为完好衬砌的最小安全系数。

3 计算结果及分析

3.1 组合缺陷对衬砌内力分布的影响

隧道拱顶、单侧拱腰、双侧拱腰3类典型部位存在不同组合缺陷时，衬砌轴力和弯矩分布分别如图3~5所示。图中以拱顶位置为0°，按逆时针方向展开得到衬砌各截面位置。如左拱腰、左边墙、左墙脚及仰拱中心部位分别对应=45°，90°，113°和180°。由图可知，缺陷的存在改变了衬砌局部刚度及其与围岩的接触状态，从而引起衬砌内力分布的明显变化，但衬砌内力影响范围及其影响程度随缺陷部位和缺陷程度不同而异。

当隧道拱顶存在组合缺陷时，衬砌各截面轴力随缺陷程度的增加均逐渐减小，而衬砌弯矩受影响范围主要集中在空洞及其临近范围，其弯矩值出现反转，并随缺陷程度的增加逐渐增大，余下部位弯矩变化较小。如从无缺陷到拱顶空洞30°且厚度减薄1/8时，拱顶部位轴力由221 kN减小至184.1 kN；弯矩由37.1 kN·m变为−19.5 kN·m，该部位由内侧受拉状态变为外侧受拉状态。相同减薄比条件下(=1/8)，拱顶空洞范围由30°增大到60°时，轴力减小了60.4 kN，弯矩增大了17.2 kN·m，变化较明显。相同空洞范围条件下(=30°)，拱顶减薄比由1/8到1/2，轴力仅减小8.2 kN，弯矩增大了0.2 kN·m，变化较小。说明衬砌内力受空洞的影响更大。

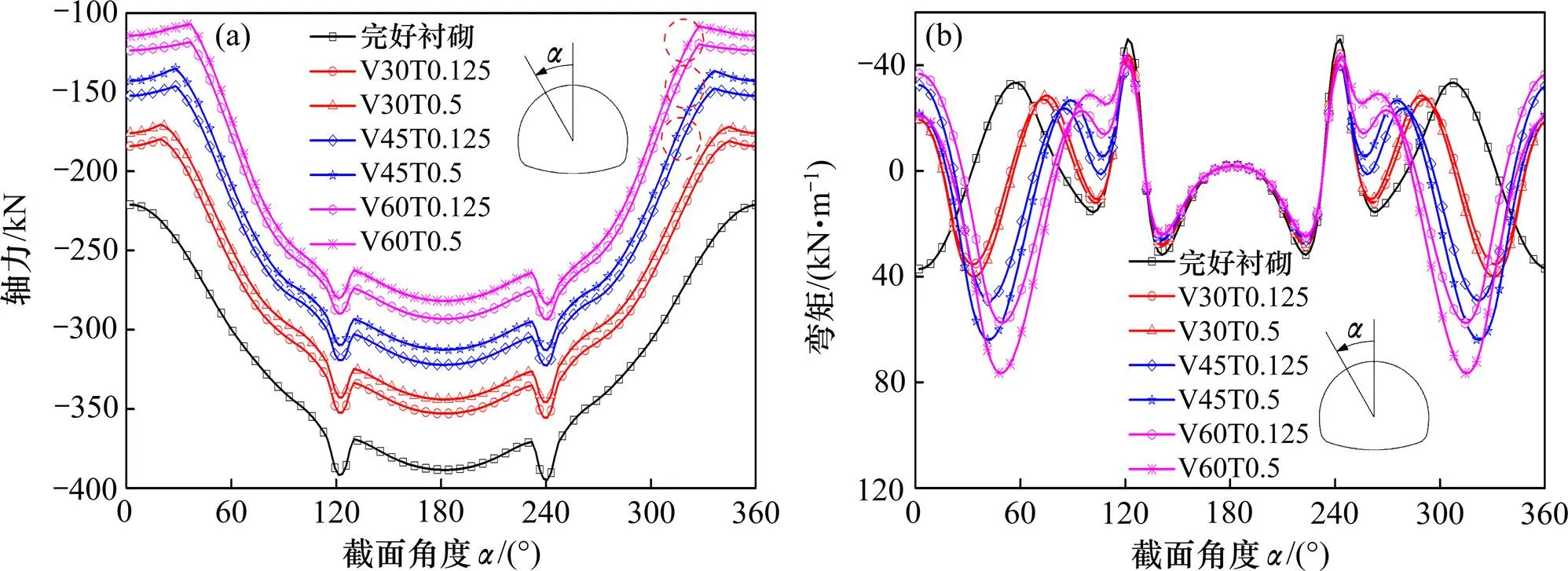
(a) 轴力；(b) 弯矩

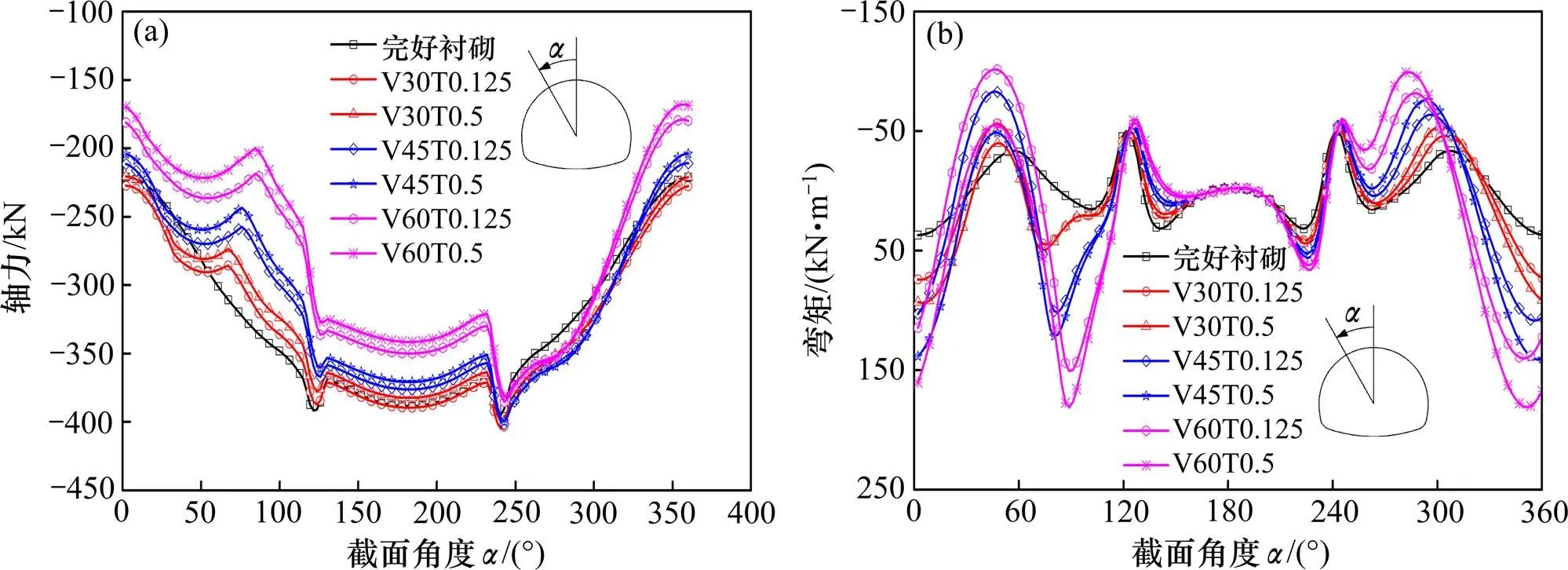
(a) 轴力；(b) 弯矩

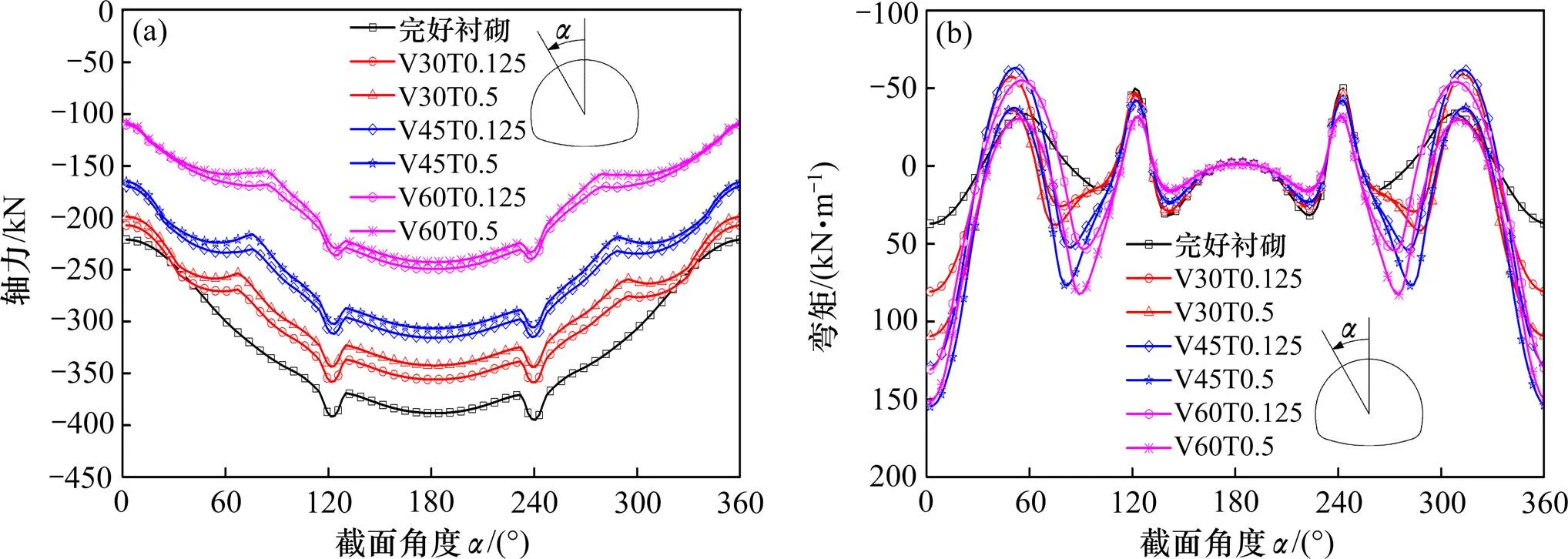
(a) 轴力；(b) 弯矩

当隧道左侧拱腰存在组合缺陷时，衬砌轴力和弯矩由对称分布向非对称分布变化，缺陷程度也大，不对称分布特征越明显。随缺陷程度的增加，缺陷附近范围内的衬砌轴力逐渐减小、弯矩明显增大。当隧道两侧拱腰均存在组合缺陷时，其对衬砌内力的影响明显大于单侧拱腰存在缺陷的情况。其内力分布规律与拱顶缺陷工况类似，但拱顶弯矩未发生反向变化，仅随缺陷程度的增加逐渐增大。此外，这2种典型部位缺陷，衬砌内力受空洞的影响较减薄明显，表现出与拱顶缺陷相同的变化规律。

3.2 组合缺陷对衬砌安全性的影响

3.2.1 衬砌安全系数的分布

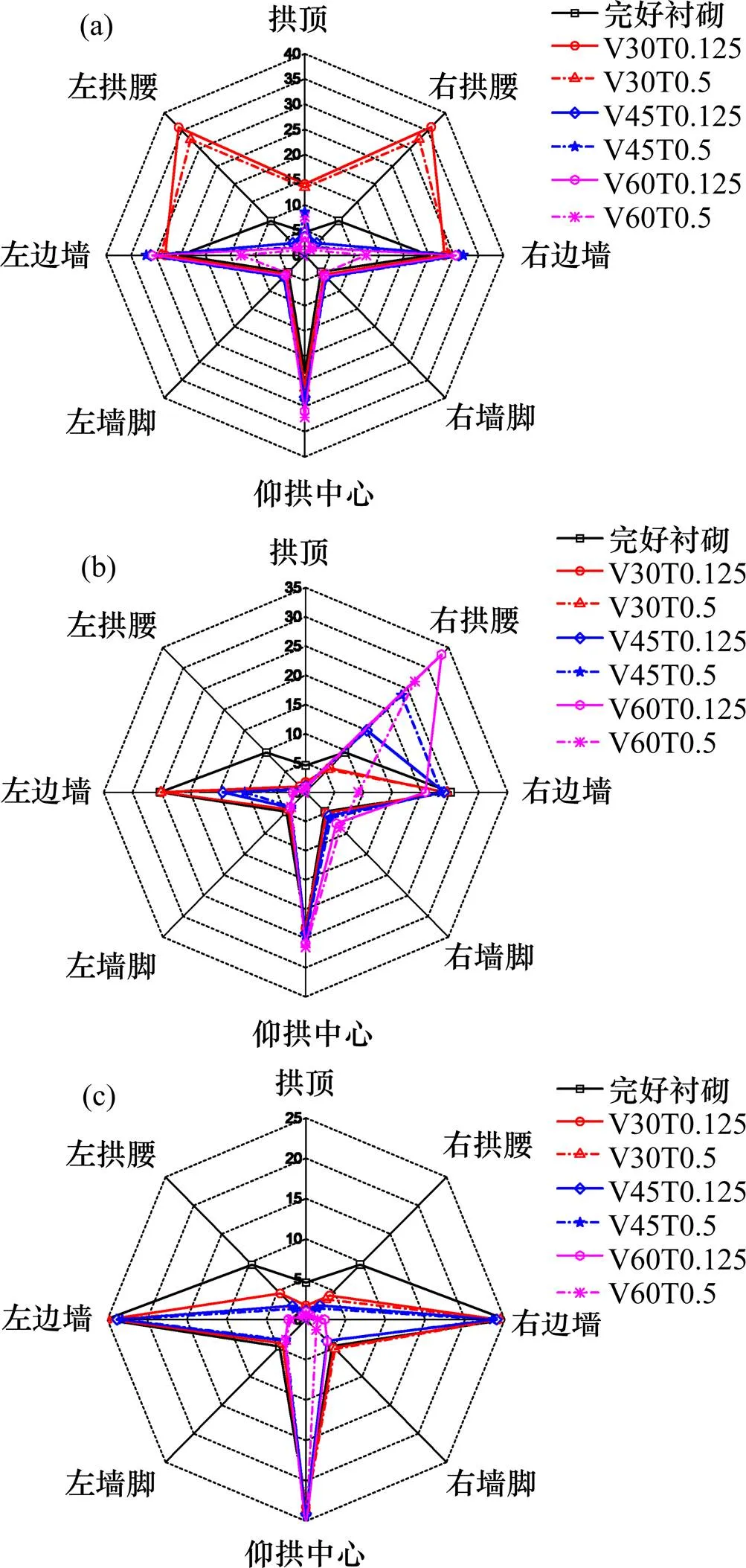
不同组合缺陷下衬砌各截面安全系数分布见图6。由图6可知，缺陷对安全系数的影响主要集中在缺陷范围及其临近部位。拱顶存在组合缺陷时，当缺陷范围由30°扩大到60°时，衬砌安全系数受影响区域由两侧拱腰之间约90°范围扩大到边墙以上180°范围。左侧拱腰存在组合缺陷时，拱顶与左边墙之间范围内的结构安全系数会受到明显影响。缺陷程度越大，安全系数的变化也越大。与完好衬砌相比，当拱顶缺陷较小时(如空洞角度=30°)，衬砌各截面安全系数未见减小；但当缺陷较大时，安全系数逐渐减小。左拱腰存在组合缺陷时，安全系数呈不对称分布。衬砌拱顶和拱腰截面安全系数均随缺陷程度增加而明显下降，其中左拱腰安全系数的下降幅度大于右拱腰。两侧拱腰都存在缺陷时，衬砌拱顶和左拱腰截面安全系数的变化规律与单侧拱腰缺陷相似，但衬砌安全系数呈对称分布，即右拱腰安全系数随缺陷程度的增加，其下降幅度与左拱腰相同。

3.2.2 衬砌安全性影响系数分析

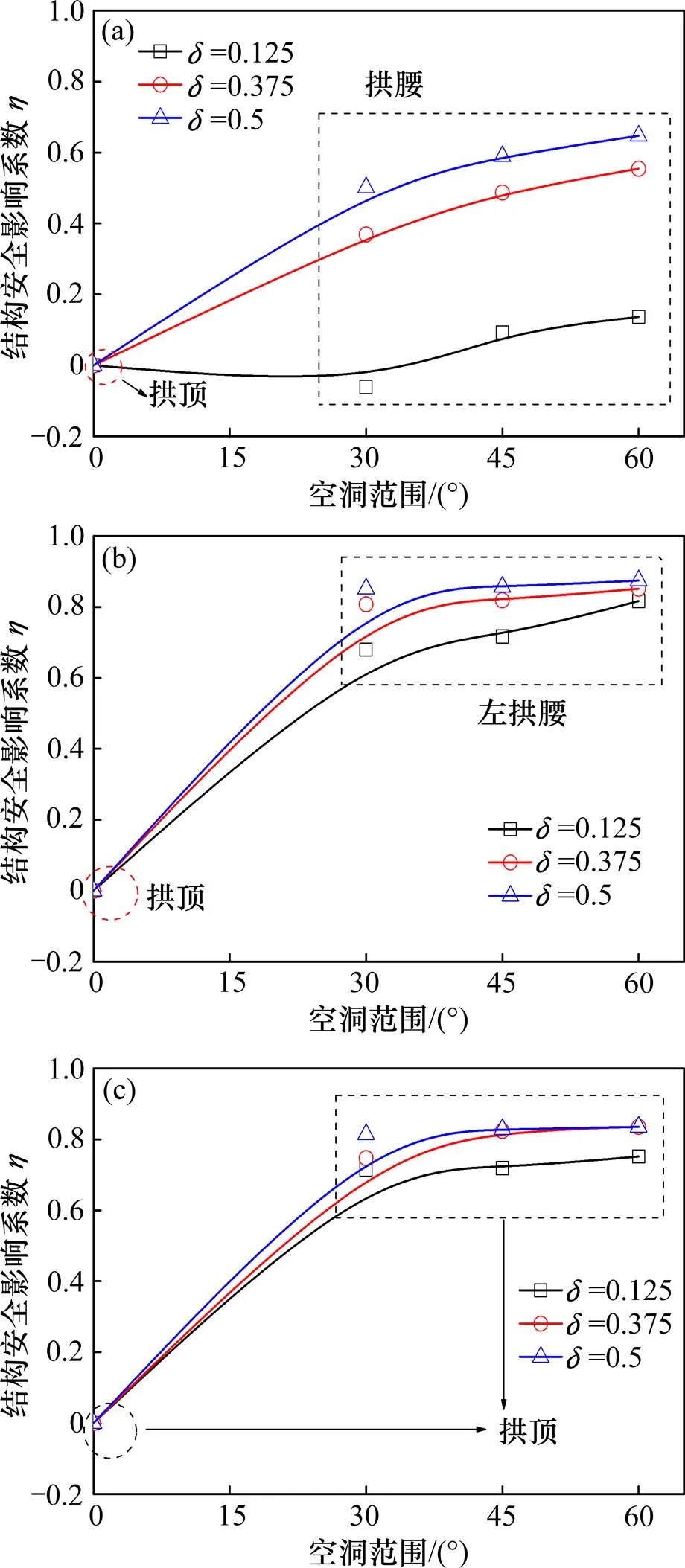
组合缺陷下衬砌安全性影响系数的变化曲线如图7所示。当拱顶存在组合缺陷时，随着缺陷程度的增加，安全性影响系数基本呈线性增长。当厚度减薄较小时(如=1/8)，安全性影响系数随空洞角度的增大，其增速较缓慢；当厚度减薄较大时(如=1/2)，安全性影响系数的增速明显增大。而且，随着缺陷程度的增大，结构安全性影响系数的最大值发生部位由拱顶向拱腰偏移。当单侧或双侧拱腰存在组合缺陷时，随着缺陷程度的增加，安全性影响系数呈两阶段增大规律。当缺陷程度较小时，安全性影响系数即迅速增大，其值达到0.7~09，之后随着缺陷程度的增加逐步趋于平缓。说明拱腰组合缺陷的影响明显大于拱顶部位，较小的组合缺陷都会对结构安全性造成较大的影响。由图7还可看出，安全性影响系数能清晰地表示不同部位、不同程度缺陷对结构安全性的影响程度。

(a) 拱顶缺陷；(b) 左侧拱腰缺陷；(c) 两侧拱腰缺陷

3.2.3 衬砌危险截面分析

将安全系数小于规范值，即强度不满足要求的截面称为危险截面，其占全断面的百分比统计结果如图8所示。当拱顶空洞小于45°时，未出现危险截面，之后危险截面占比随缺陷程度的增大而快速增加。拱顶空洞角度从45°增大到60°时(=1/8)，危险截面占比由6.1%增大到15.2%，这是缺陷越大，衬砌受缺陷影响的范围越大，不断恶化衬砌的受力状态，使得危险截面占比迅速增多。拱腰存在组合缺陷时，衬砌危险截面占比变化规律与拱顶类似，但受缺陷的影响程度大于拱顶部位。

(a) 拱顶缺陷；(b) 左侧拱腰缺陷；(c) 两侧拱腰缺陷

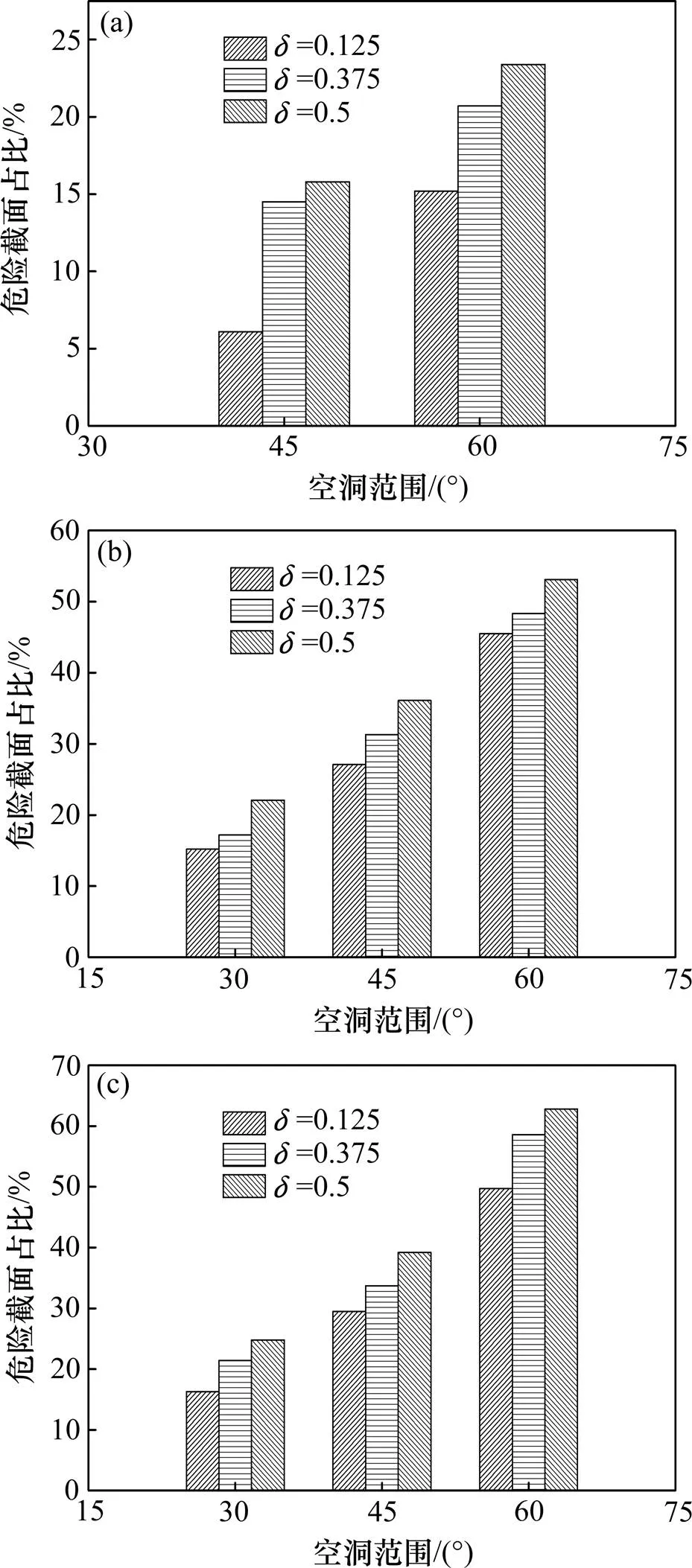
(a) 拱顶缺陷；(b) 左侧拱腰缺陷；(c) 两侧拱腰缺陷

4 结论

1) 基于空洞附近范围内存在围岩应力集中现象，在现有荷载修正模型基础上，采用梯形面积等效建立了围岩压力的修正计算方法。

2) 衬砌厚度不足和背后空洞的存在会改变衬砌局部刚度及其与围岩的接触状态，从而引起衬砌内力重分布。衬砌内力的影响范围及其影响程度随缺陷部位和缺陷程度不同而迥异。总体而言，缺陷越大，衬砌受影响范围越大；影响范围内的衬砌轴力减小，弯矩增大，恶化了结构受力状态。比较而言，衬砌内力受空洞的影响较厚度减薄更明显。

3) 衬砌缺陷的影响主要集中在缺陷处及其邻近部位，缺陷程度越大，安全系数下降越为明显。当拱顶存在组合缺陷时，随着缺陷程度的增加，安全性影响系数基本呈线性增长；而当单侧或双侧拱腰存在组合缺陷时，则呈两阶段非线性增长。从安全性影响系数和危险截面占比可看出，拱腰组合缺陷的影响大于拱顶部位，较小的组合缺陷条件下就会对结构安全性造成较大的影响。

[1] 洪开荣. 近 2 年我国隧道及地下工程发展与思考(2017~2018年)[J]. 隧道建设(中英文), 2019, 39(5): 710−723. HONG Kairong. Development and thinking of tunnels and underground engineering in China in recent 2 years (from 2017 to 2018)[J]. Tunnel Construction, 2019, 39(5): 710−723.

[2] 吴江滨, 张顶立, 王梦恕. 铁路运营隧道病害现状及检测评估[J]. 中国安全科学学报, 2003, 13(6): 49−52. WU Jiangbin, ZHANG Dingli, WANG Mengshu. Current damage situation of railway operation tunnels and their inspection and evaluation[J]. China Safety Science Journal, 2003, 13(6): 49−52.

[3] 陈建勋, 罗彦斌, 姜久纯. 运营公路隧道安全评估[J]. 现代隧道技术, 2006, 43(4): 68−71. CHEN Jianxun, LUO Yanbin, JIANG Jiuchun. The safety assessment of a road tunnel[J]. Modern Tunnelling Technology, 2006, 43(4): 68−71.

[4] 张素磊. 隧道衬砌健康诊断及技术状况评定研究[D]. 北京: 北京交通大学, 2012. ZHANG Sulei. Study on health diagnosis and technical condition assessment for tunnel lining structure[D]. Beijing: Beijing Jiaotong University, 2012.

[5] 张博. 云南山区公路隧道衬砌病损特征及服役状况评价方法研究[D]. 昆明: 昆明理工大学, 2018. ZHANG Bo. Study on the damage characteristics and service status evaluation methods of highway tunnel lining in Yunnan mountain area[D]. Kunming: Kunming University of Science and Technology, 2018.

[6] 佘健, 何川, 汪波, 等. 衬砌背后空洞对隧道结构承载力影响的模型试验研究[J]. 公路交通科技, 2008, 25(1): 104−110. SHE Jian, HE Chuan, WANG Bo, et al. Study on effect of cavities behind linings on bearing capacity of tunnel structure by model test[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 104−110.

[7] 汪波, 李天斌, 何川, 等. 衬砌减薄对隧道结构承载力影响的模型试验研究[J]. 铁道学报, 2013, 35(2): 106− 114. WANG Bo, LI Tianbin, HE Chuan, et al. Model test of effect of lining thinning on tunnel structure bearing capacity[J]. Journal of the China Railway Society, 2013, 35(2): 106−114.

[8] 张旭, 张成平, 冯岗, 等. 衬砌背后空洞影响下隧道结构裂损规律试验研究[J]. 岩土工程学报, 2017, 39(6): 1137−1144. ZHANG Xu, ZHANG Chengping, FENG Gang, et al. Experimental studies on effect of voids behind tunnel linings on progressive failure process of tunnel structures[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1137−1144.

[9] DING Zude, JI Xiafei, LI Xiaoqin, et al. Influence of symmetric and asymmetric voids on mechanical behaviors of tunnel linings: model tests and numerical simulations[J]. Symmetry, 2019, 11(6): 1−19.

[10] 李彬, 雷明锋, 李文华. 运营公路隧道病害对衬砌结构安全性的影响[J].铁道科学与工程学报, 2011, 8(5): 40−45. LI Bin, LEI Mingfeng, LI Wenhua. Safety influence of operating highway tunnel caused by sturcture disease[J]. Journal of Railway Science and Engineering, 2011, 8(5): 40−45.

[11] WANG J F, HUANG H W, XIE X Y, et al. Void-induced liner deformation and stress redistribution[J]. Tunneling and Underground Space Technology, 2014, 40: 263−276.

[12] 王春景, 雷明锋, 彭立敏. 病害隧道结构安全性评价模型与方法[J]. 铁道科学与工程学报, 2011, 8(3): 73−77. WANG Chunjing, LEI Mingfeng, PENG Limin. Safety evaluation model and method of tunnel disease sturcture[J]. Journal of Railway Science and Engineering, 2011, 8(3): 73−77.

[13] 张成平, 张旭, 冯岗, 等. 衬砌厚度不足对隧道结构安全性的影响分析[J]. 现代隧道技术, 2017, 54(2): 134− 143, 169. ZHANG Chengping, ZHANG Xu, FENG Gang, et al. Influence of insufficient lining thickness on the safety of a tunnel structure[J]. Modern Tunnelling Technology, 2017, 54(2): 134−143, 169.

[14] 叶艺超, 彭立敏, 雷明锋, 等. 不同脱空模式下隧道结构安全状态分析[J]. 铁道科学与工程学报, 2018, 15(11): 2875−2883. YE Yichao, PENG Limin, LEI Mingfeng. Safety analysis of tunnel structures with different patterns of voids behind lining[J]. Journal of Railway Science and Engineering, 2018, 15(11): 2875−2883.

[15] 应国刚, 张顶立, 陈立平, 等. 荷载结构模型在拱顶空洞存在情况下的修正[J]. 土木工程学报, 2015, 48(增1): 181–185. YING Guogang, ZANG Dingli, CHEN Liping, et al. Amendment of load-structure model with voids behind tunnel lining at vault[J]. China Civil Engineering Journal,2015, 48(Suppl 1): 181−185.

[16] 聂子云, 张春雷, 李凤翔. 衬砌背后空洞对隧道抗震性能影响分析[J]. 地震工程学报, 2015, 37(1): 138–143. NIE Ziyun, ZHANG Chunlei, LI Fengxiang. Effect of void behind lining on seismic performance of tunnel[J]. Chinese Earthquake Engineering Journal, 2015, 37(1): 138−143.

[17] 丁祖德, 张博, 李晓琴, 等. 衬砌脱空对隧道地震响应影响的振动台试验研究[J]. 振动与冲击, 2018, 37(14): 156−161. DING Zude, ZHANG Bo, LI Xiaoqin, et al. Shaking table tests for investigating the effect of void behind lining on the seismic responses of a tunnel[J]. Journal of Vibration and Shock, 2018, 37(14): 156−161.

[18] JTG 3370.1−2018, 公路隧道设计规范第一册土建工程[S]. JTG 3370.1−2018, Specifications for design of highway tunnels Section 1 civil engineering[S].

Analysis of stress characteristics of lining structure under the influence of combined defects

YIN Hongbo, LIU Zhengchu, GUO Yongfa

(Kunming Survey, Design and Research Institute Company Limited of CREEC, Kunming 650200, China)

Based on surrounding rock pressure amendment approach, a load-structure model for two-lane- highway mountain tunnel in Yunnan Province was established. By introducing the safety influence coefficient of the lining, the stress characteristics of the lining under the influence of the combined defects which include voids and insufficient thickness at the back of the lining are analyzed. Modelling results showed that the combined defects would change the local stiffness of lining and its contact with the surrounding rock , and thus led to the internal force redistribution of the lining. The influence of lining defects mainly affected the deteriorated zones and their adjacent regions, and the greater the degree of the defect is, the larger the affected area of the lining is. In these deteriorated zones, the internal axial force of the lining dropped dramatically and the bending moment rose up in accordance, which lowered down the safety factor and further worsen the stress state of the whole lining structure. In addition, if the combined defects existed in the tunnel crown, the safety influence coefficient of the lining (deterioration ratio) increased linearly with the increasing of the defect level. While, this ratio showed a bilinear growth law if the combined defects existed in one or two sides of the haunch. Furthermore, comparatively speaking, the influence of void on structural safety is greater than that of insufficient lining thickness. It was worthy note that, the influence of the combined defects at the haunch is greater than those that at the crown; and most importantly, smaller combined defects would impose a significant impacts on the structural safety of tunnel.

mountain tunnel; void behind lining; insufficient lining thickness; amendment of surrounding rock pressure; influence coefficient

U451

A

1672 − 7029(2020)08 −2037 − 09

10.19713/j.cnki.43−1423/u.T20190874

2019−10−09

云南省重点研发计划资助项目(社会发展领域)(2018BC008)

殷洪波(1976−)，男，云南昆明人，高级工程师，从事隧道设计及相关研究工作；E−mail：345492720@qq.com

(编辑 蒋学东)