基于APSO的地铁节能运行速度优化研究

杨辉，李莹，周艳丽

基于APSO的地铁节能运行速度优化研究

杨辉1, 2，李莹1, 2，周艳丽1, 2

(1. 华东交通大学 电气与自动化工程学院，江西 南昌 330013；2. 江西省先进控制与优化重点实验室，江西 南昌 330013)

当前城轨列车多站间节能运行优化研究中，牵引能耗模型未考虑实际运行状态，仅由列车控制力与运行速度2个指标决定，且广泛采用固定运行模式，难以根据实际环境动态调整。依据列车实际运行过程，首先探究运行时间和站间距离对运行能耗的影响，并对同一站间距离的节能运行工况进行分析，研究工况的转换序列，进而重建能耗优化模型，最后采用改进的粒子群算法求解工况转换点，以实现列车速度曲线节能优化。仿真结果表明，重构的能耗优化模型与传统模型对比精度提高了1.16%，且优化后的运行能耗比原固定驾驶策略节省了6.92%，具有更好的节能效果。

城轨列车；牵引能耗；速度优化；工况转换；改进粒子群算法

随着城轨列车运营里程增加，客运量不断攀升，地铁牵引能耗持续增长，节能降耗已成为轨道交通可持续发展所必须要解决的问题之一[1]。目前，国内外针对城市轨道交通列车运行能耗的计算，多由列车控制力与运行速度所决定，未考虑列车运行过程中的实际运行状态。因此，研究多站间运行速度曲线节能优化，需考虑列车节能运行工况、站间距及运行时间对列车牵引能耗计算模型的影响，对模型的准确性和节能效果具有重要的现实意义。针对列车牵引能耗建模和速度曲线节能优化的问题，国内外众多学者进行了深入的研究和探索。Scheepmaker等[2−3]利用列车运行过程中受到的合力和速度的乘积计算列车牵引能耗。王黛等[4]通过分析机车类型、停站方案等牵引能耗影响因素，利用BP神经网络建立动车组牵引能耗计算模型。陆垚等[5]分析列车属性的差异对牵引能耗的影响，进而探究在不同类型的线路上列车节能运行的适应性。黄金等[6]结合不同级位下牵引效率特点，建立能耗计算模型。宁晶洁[7]利用“牵引−惰性−制动”的3阶段模式进行列车节能控制，以牵引能耗之和最小为目标，求解列车在各个站间的牵引、制动持续时间。宋文婷等[8]基于4阶段操纵模式提出离线全局优化和在线局部优化的速度曲线寻优方法。但上述列车能耗模型的建立只考虑列车属性、操纵级位及牵引效率等对能耗的影响，未考虑列车运行过程中的实际状态，且列车多站间运行过程广泛采用固定的运行工况，在速度曲线的优化中实际操作适用性较差。针对上述问题，本文首先分析列车运行能耗与运行时间、站间距离的影响规律，建立传统模型加未建模动态部分的能耗计算模型，通过对同一站间距离的节能运行工况进行分析，研究符合实际运行的工况转换序列，利用改进粒子群算法求解工况转换点，通过将能耗优化模型和传统模型的计算结果与实际能耗进行对比分析，验证模型的准确性。最后将不同节能运行工况下的能耗值进行比较，寻找适应不同站间距离下的能耗最小的运行工况，进一步达到更好的节能效果。

1 同一站间距离不同节能运行工况分析

城市轨道交通列车在规定的运行时间内存在多条运行速度曲线，由于不同速度曲线带来的列车牵引位置和距离不同，导致列车在站间运行的能耗不同[9]。研究同一距离下的单车节能速度曲线的问题，旨在求解列车在站间的节能速度曲线，本文通过建立考虑列车运行状态的列车速度曲线优化模型，对比分析后的列车控制序列，得到同一站间距下的最小牵引能耗。

1.1 列车节能运行工况及其转换序列

城轨列车运行过程中能耗值的差异由列车驾驶策略[10]所决定。通过分析庞特里亚金最大值原理，可知“最大加速度牵引MA—巡航PB(部分制动) —惰行C—最大减速度制动MB”为节能驾驶策略[11]，但列车在实际运行过程中，需考虑工况间转换序列的适应性。假设站间距离已知，将站间区段划分为个区间，且区间内的限速和坡度固定，进而根据转换点的数量分析区间内的节能运行工况转换序列[12]。

1.1.1 区间存在一个工况转换点

列车节能运行工况1共有4种，可知其区段内可能存在的转换序列有12种，经分析列车在区间只存在一个工况转换点的节能转换序列如表1。即为MA-MB，MA-C，C-PB，MA-PB，C-MB和PB- MB。

表1 存在1个工况转换点的节能转换序列

1.1.2 区间存在2个工况转换点

依据工况转换点的位置，将区间分别作为固定线路信息的2个独立的子区间，其有且仅有1个工况切换点，例如在区间内MA-C-MB为转换序列，子区间分别为MA-C，C-MB，此时的惰性点为区间工况切换点，则以下序列为其区间内可能存在的转换序列：MA-MB，MA-C，C-PB，MA-PB，C-MB和PB-MB。假设列车运行在陡坡区间，此时列车运行工况为部分制动，一旦不施加外力速度不断增大，通过分析PB-MA可知，此时列车工况切换至牵引，将超出限速，因此不存在PB-MA和PB-C转换序列。由于牵引切换至惰性时，可更大程度上降低能耗，因此排除C-MA序列。因此，将区间存在2个转换点的工况转换序列归纳为C-PB-MB，MA- C-MB，MA-C-PB和MA-PB-MB。

1.1.3 区间存在多个工况转换点

与上节类似，将存在多个工况转换点的区间看作多个子区间，且其各个子区间的转换序列与上述转换序列一致，一旦列车运行速度超出限制值，将从牵引工况转换至惰性，而列车为达到目标速度，再次切换至加速状态，因此反复出现C-MA的转换序列。因此，区间存在多个工况转换点的工况转换序列可归纳为MA-C(MA-C-MA-C)，MA-C-PB-MB和MA-C-(MA-C)-MB。

根据转换点数量的不同，分析可知区间内可能存在的节能工况转换序列如图1所示。

(a) MA-(C-MA-对)-C-MB；(b) MA-C-MB；(c) MA-C-PB-MB

2 列车牵引能耗模型的建立

列车在站间运行过程中，牵引能耗受诸多因素的影响，而传统的能耗模型由列车运行中所受合力和速度的乘积计算而得，但当目标速度过大时，其计算相对误差增大，导致在计算牵引能耗时存在一定的局限性，且节能运行模型建立的准确程度对列车站间能耗的仿真结果有着决定性的作用，因此本节分析站间运行时间及站间距对牵引能耗的影响。

2.1 未知因素(距离、时间)与能耗的关系

由于站间距和站间运行时间在不同工况下对能耗有着不同影响，各种工况下的能耗影响模型无法精确获得。为了减小列车操纵方式对运行能耗的影响，采用设置巡航速度的方法来研究在相同停站次数下站间距对运行能耗的影响，对固定的区间设定不同的站间运行时间，得到对应的能耗值[13]。

将两者对列车牵引能耗的影响因素曲线绘制如图2~3，通过分析影响因素特性曲线，发现列车单位距离运行能耗随着站间距的增大而减小，且由图4可知，单位距离运行能耗降低率减小的趋势逐渐趋于平缓；而同一站间距下运行能耗随着运行时间的增加而减小，由此可知两者对牵引能耗都有一定影响。

图2 能耗−距离曲线示意图

通过探究站间距及运行时间与牵引能耗的影响，可知单位距离运行能耗是随站间距增加而减小，由此可表示为站间距的一元多项式，同时采用多项式回归来建立数学模型；在运行时间与能耗的关系曲线中，根据能耗随运行时间的变化特点，分别利用多项式回归分析法和幂逼近法进行分析对比，进而采用最小二乘法进行拟合，为了使模型形式尽量简约且易于解释和应用，同时尽可能不损失误差的自由度来保证拟合精度，采用逐阶分析法，通过综合比较调整测定参数、均方差等来确定最优的运行时间、站间距与运行能耗的数学模型。

图3 能耗-时间曲线示意图

图4 单位距离运行能耗降低率

通过Matlab对站间运行时间及站间距与牵引能耗关系的曲线进行拟合，得到该影响因素模型用式(1)描述：

式中：1()代表距离与运行能耗间的关系；2()代表能耗随运行时间的变化情况；和为两者对牵引能耗影响程度的权重，其中1和2为列车运行过程中运行阻力，包括风阻及车辆内部零件的摩擦力等所消耗的能量，2为单位时间能耗变化率，1为单位距离能耗变化率，1为单位位移能耗的影响因子，2为单位时间能耗的影响因子。同时可得关系曲线图6~7，从图中可以看出所建立的影响因素模型与实验数据拟合效果良好。因此，站间距及运行时间与牵引能耗的影响因素模型成立。

2.2 考虑未知因素的列车节能运行优化模型

列车从车站出发运行至下一车站，根据工况转换点不同，由上述分析可知有3种节能工况序列。保证列车在安全运行的前提下，求解列车在站间运行过程中的速度曲线节能优化问题，寻找满足准点、精准停车、舒适性要求下牵引能耗最低的工况转换点。通过分析站间距及运行时间对能耗影响，从牵引能耗的角度建立列车节能优化数学模型：

式中：为列车站间运行总时间；为列车站间运行距离；()为随速度变化的牵引力；为列车在站间运行的能耗；1()，2()为随距离、时间变化的关于能耗的函数；为由牵引力所计算的能耗的权值；()为列车在运行过程中相应位置上限速的约束，为列车加(减)速度；limit为允许的最大加(减)速度。

运行能耗随距离、时间变化的影响因素模型：

式中：代表列车运行的站间距离，代表列车运行时间。该函数通过对数函数表示列车运行状态中能耗随距离、时间所变化的实际变化情况，当站间距离增大时，列车运行能耗随之增大；当列车站间运行时间越长，其列车能耗随之增加。

根据牛顿第二定律可得经典的运动学模型：

式中：为列车重量，列车所施加的牵引力和制动力受最大牵引力和最大值动力的约束()ϵ[0,1]，()ϵ[0,1]，在此基础上可对目标函数进行计算。

2.3 2种模型计算结果比较

为了更好地描述重建模型与传统模型的能耗计算准确度，在固定列车的基本参数(列车长度、列车质量等)、列车区间运行的限制速度、区间坡度及曲线半径等的条件下，利用2种能耗计算模型分别从运动方程出发，根据实际运行速度曲线分析每个时间步长(3.5 s)内列车的受力情况，对该列车运行区间进行牵引能耗值的计算，并与实际能耗值进行对比，得到2种模型的能耗计算相对误差。并将两者与实际运行能耗间的计算相对误差绘制如图5。

图5 单位距离运行能耗降低率

从图5可得：重建的能耗优化模型的能耗计算值与实际列车运行能耗的相对误差在4.21%，而传统模型的能耗计算值与实际能耗相对误差在8.79%。通过54组数据分别利用2种能耗计算模型在同一实验条件下进行仿真验证，重建模型的能耗计算相对误差比传统模型小的共有52组，由此可知，重建的能耗优化模型用于计算列车牵引能耗的准确性更高。由于传统模型中列车运行牵引能耗仅由合力和速度2个指标决定，其牵引阶段能耗计算的相对误差较大，其原因是当目标速度增长率增大时，能耗计算模型与实际列车运行能耗之间存在一定误差，而建立考虑运行时间及站间距综合作用下的能耗优化模型，可减小由实际运行状态而导致的计算误差，使重建的能耗优化模型比传统模型能够更好地计算列车牵引能耗。

3 APSO算法对模型的求解

本文所建立的能耗优化模型属于非线性约束变量优化问题，而粒子群算法[14]具有搜索速度快、效率高、算法简单等特点，因此广泛应用于科学研究和工程优化设计领域[15−16]。本文采用可根据适应值自适应调节惯性权重的改进快速粒子群算法(APSO)[16]提高算法的性能，以寻找使得牵引能耗最低的节能速度曲线的工况转换点。

将节能速度曲线优化模型作为改进粒子群算法适应度函数，采用APSO算法分别求解3种不同的节能运行工况转换点，对比优化后的牵引能耗值，以此得到一条更加合理的节能运行速度曲线。下面为求解列车节能控制优化问题的具体步骤：

1) 设置算法参数，群体的规模，粒子加速因子1和2，最大最小惯性权重max和min，最大速度max，粒子的维数为(即列车工况转换点的 数量)。

2) 从迭代条件出发，初始化粒子群位置x(列车运行中可能的工况转换点)和速度v(每个工况转换点位置改变的量)，故粒子群位置矩阵表示为：

其中：v为[−max,max]区间范围内的随机数。

3)将目标函数式(2)中的牵引能耗数值作为每个粒子的个体适应度值f,=1,2,…,。

4) 用每个粒子当前的适应度值f与历史最优适应度值p进行比较，若当前适应度值f小于p，则将其更新为历史最优值，由此求出整个群体的全局最优值。

5)对群体中各粒子的速度进行调整：

式中：1和2为[0,1]均匀分布随机数。

本文采用一种惯性权重自适应调整策略，即惯性权重是根据当前的适应值进行调节的，其表达式如下：

式中：为当前粒子的适应值；ave为适应值的平均值；min为最小适应度值。

6)更新群体中各粒子的位置：

7) 检查更新后粒子的有效性，若处于无效状态则重新进行初始化。

8) 判断是否达到结束条件(一个为最大迭代次数；另一个是在指定范围内的适应度值的偏差)。若是，则结束迭代，否则转到(3)继续进行迭代求解。

4 实例分析

选用北京某地铁线路[7]为案例，线路运营里程总计23.3 km，列车的基本参数见表2~3，式中：和为牵引力和制动力；0为列车运行的总阻力，kN；m为动车的总质量，t；t为拖车的总质量，t；为列车的编组。

表2 城市轨道交通列车基本参数

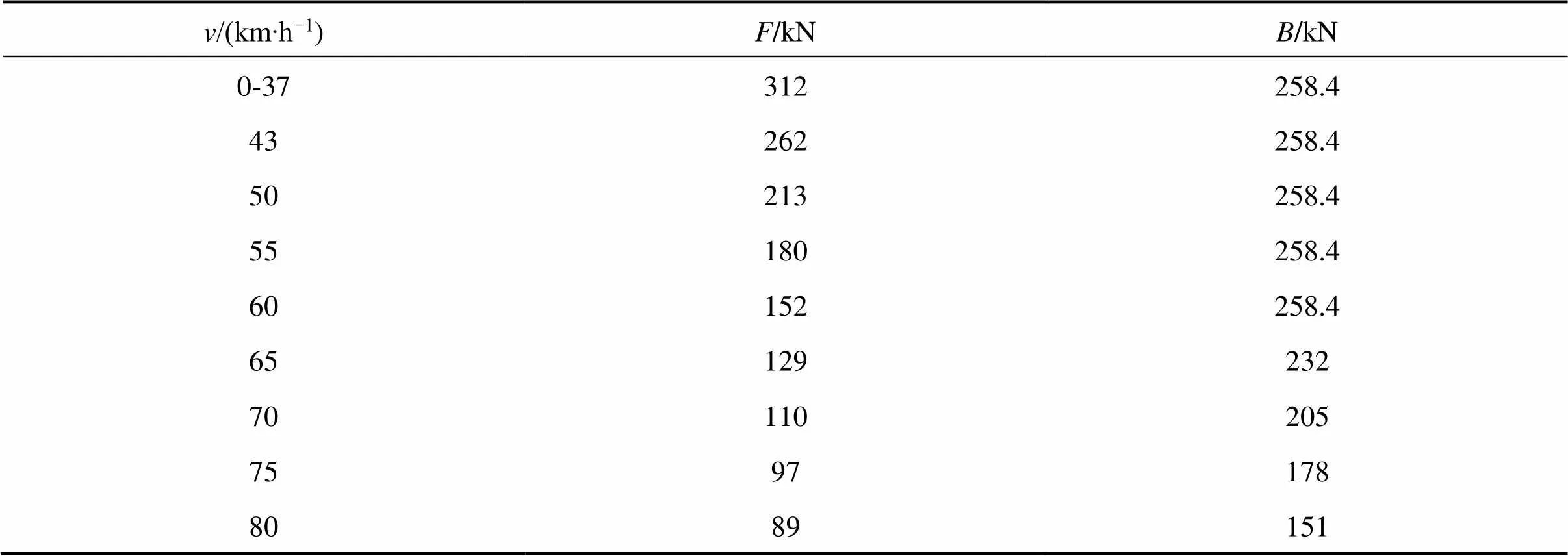
表3 列车的牵引和制动特性

通过Matlab对站间运行时间及站间距与牵引能耗关系的曲线进行拟合，得到1，1，1，2，2和2为6.566，7 254，5.013×106+06，1.79×104，−1.605和8.315。拟合后两者对牵引能耗的影响与原影响因素曲线对比如图6~7。

图6 拟合后能耗-时间曲线

图7 拟合后能耗−距离曲线

设置算法群体规模取为30，最大迭代次数为100，最大惯性权值max为0.9，最小惯性权值min为0.4，根据专家经验设置为0.8，为0.1，为0.1。最大加速度因子1为2，2为2.1，粒子最大速度max为150，列车牵引系数取0.95，制动系数取0.8，区间线路的限制速度为80 km/h，列车最大加速度为0.8 m/s2，最大减速度为0.6 m/s2。本章在不同区间下，采用基于重建能耗优化模型的列车站间节能优化方法，分别求解列车3种不同节能运行策略的工况切换点，并计算其牵引能耗数值，具体结果如表4~6所示。

然后依次优化各站间不同运行策略下的工况切换点及其能耗，通过对比得到最优节能速度曲线，并与原运行策略进行对比如表7。最小运行时间下的能耗明显大于原运行策略和节能运行策略下的能耗，列车站间节能运行策略可根据不同站间距离及运行状态所得，通过在站间距较大的区间如区间1，3，4，9和10，采用MA-C-PB-MB节能运行工况，在站间距较小的区间如5，若仍采用MA-C-PB-MB运行策略，则其节能空间不足，退化为MA-C-MB运行策略可有效减少牵引能耗。

表4 MA-(C-MA-对)-MB运行工况下的工况转换点及能耗优化结果

表5 MA-C-MB运行工况下的工况转换点及能耗优化结果

表6 MA-C-PB-MB运行工况下的工况转换点及能耗优化结果

表7 基于节能运行工况的能耗优化结果

因此，列车站间“MA-C-PB-MB”节能运行策略在大站间距区间节能空间较大，而其他节能运行策略需要根据具体列车实际运行条件而定。

案例线路[7]中13个站间区间，通过重建能耗优化模型并采用适应实际运行状态下的节能运行工况，相比于原站间运行策略(牵引−惰性−制动)，可降低10.09%的牵引能耗，且站间平均节能效果为6.92%，如图8为站间运行能耗对比图。

图8 站间运行能耗

求解列车速度曲线节能优化的APSO算法的平均适应度随迭代次数的变化情况如图9所示，其随着迭代次数的增加，在20次迭代之前有显著增长，且40次迭代之后平均适应度趋于最优解。

图9 APSO算法平均适应度的迭代情况

5 结论

1) 通过探究运行时间和站间距离2个指标对运行能耗的影响，建立传统模型加未建模动态部分的能耗优化模型；以降低全线多站间总牵引能耗为目标，研究同一站间距离下运行工况的转换序列，并结合重建的能耗优化模型，对比分析不同运行策略下的牵引能耗，采用改进的粒子群算法实现了列车的多目标速度曲线节能优化。

2) 以北京某地铁线路为例，算例分析表明，重构的能耗优化模型与传统模型对比精度提高了1.16%，且优化后的运行能耗比原固定驾驶策略节省了6.92%，验证了优化节能运行策略的节能效果。

3) 在城市轨道交通列车运行能耗管理工作中，优化考虑列车运行状态的各站间节能运行工况和牵引能耗模型，可提供更为合理的城市轨道列车节能运行优化方案。

[1] González-Gil A, Palacin R, Batty P. Optimal energy management of urban rail systems: Key performance indicators[J]. Energy Conversion and Management, 2015, 90(1): 282−291.

[2] Scheepmaker G M, Goverde R M P, Kroon L G. Review of energy-efficient train control and timetabling[J]. European Journal of Operational Research, 2017, 257(2): 355−376.

[3] SU Shuai, TANG Tao, LI Xiang, et al. Optimization of multi-train operations in a subway system[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 673−684.

[4] 王黛, 马卫武, 李立清, 等. 基于BP神经网络的高速动车组牵引能耗计算模型[J]. 中南大学学报, 2017, 48(4): 1104−1110. WANG Dai, MA Weiwu, LI Liqing, et al. Calculation model of traction energy consumption for high-speed EMUs based on BP neural network[J]. Journal of Central South University, 2017, 48(4): 1104−1110.

[5] 陆垚, 毛保华, 柏赟, 等. 列车属性对城市轨道交通牵引能耗的影响及列车用能效率评价[J].中国铁道科学, 2016, 37(2): 99−105. LU Yao, MAO Baohua, BAI Yun, et al. Impact of train characteristics on traction energy consumption of urban rail transit and evaluation on train energy efficiency[J]. China Railway Science, 2016, 37(2): 99−105.

[6] 黄金, 陆阳, 贾冰. 基于牵引效率曲线的动车组能耗仿真计算[J]. 铁道机车车辆, 2018, 38(3): 6−9. HUANG Jin, LU Yang, JIA Bin. Simulation calculation of EMU energy consumption based on traction efficiency curve[J]. Railway Locomotive, 2018, 38(3): 6−9.

[7] 宁晶洁. 城市轨道交通列车运行模型及算法研究[D]. 北京: 北京交通大学电子信息工程学院, 2017: 63−71. NING Jingjie. Research on train operation model and algorithm of urban rail transit[D]. Beijing: Beijing Jiaotong University, School of Electronic Information Engineering, 2017: 63−71.

[8] 宋文婷, 谭觅, 蔡文川, 等. 高速列车的节能操纵策略研究[J]. 铁道科学与工程学报, 2016, 13(3): 423−429. SONG Wenting, TAN Mi, CAI Wenchuan, et al. Research on energy-saving maneuvering strategy of high-speed trains[J]. Journal of Railway Science and Engineering, 2016, 13(3): 423−429.

[9] YANG Songpo, WU Jianjun, YANG Xin, et al. Energy- efficient timetable and speed profile optimization with multi-phase speed limits: Theoretical analyses and application[J]. Applied Mathematical Modelling, 2018, 56: 32−50.

[10] 黄友能, 宫少丰, 曹源, 等. 基于粒子群算法的城轨列车节能驾驶优化模型[J]. 交通运输工程学报, 2016, 16(2): 118−124. HUANG Youneng, GONG Shaofeng, CAO Yuan, et al. Energy-saving driving optimization model for urban rail trains based on particle swarm optimization[J]. Journal of Traffic and Transportation Engineering, 2016, 16(2): 118−124.

[11] 冯瑜, 陈绍宽, 冉昕晨, 等. 考虑再生制动能利用的城市轨道交通列车节能运行优化方法研究[J]. 铁道学报, 2018, 40(2): 15−22. FENG Yu, CHEN Shaokuan, RAN Xinchen, et al. Study on the optimization method of energy-saving operation of urban rail transit trains considering the utilization of regenerative braking energy[J]. Journal of the China Railway Society, 2018, 40(2): 15−22.

[12] SU Shuai, TANG Tao, CHEN Lei, et al. Energy-efficient train control in urban rail transit systems[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit, 2014, 229(4): 1−9.

[13] 王玉明. 城市轨道交通系统能耗影响因素的量化分析[D]. 北京: 北京交通大学交通运输学院, 2011: 27−48. WANG Yuming. Quantitative analysis of factors affecting energy consumption of urban rail transit system[D]. Beijing: Beijing Jiaotong University, School of Traffic and Transportation, 2011: 27−48.

[14] Kennedy J, Eberhat R C. Particle swarm optimization [C]// Proceedings of IEEE International Conference on Neural Network USA: IEEE Press, 1995: 1942−1948.

[15] 方群, 徐青. 基于改进粒子群算法的无人机三位航迹规划[J]. 西北工业大学学报, 2017, 35(1): 66−73. FANG Qun, XU Qing. 3D route planning for UAV based on improved PSO algorithm[J]. Journal of Northwest University of Technology, 2017, 35(1): 66−73.

[16] 宋栓军, 陈凯凯, 张华威. 基于APSO算法的双容水箱PID参数优化仿真[J]. 计算机仿真, 2018, 35(8): 261− 265. SONG Shuanjun, CHEN Kaikai, ZHANG Huawei. Optimization of PID parameters of dual water tank based on APSO algorithm[J]. Computer Simulation, 2018, 35(8): 261−265.

Research on optimization of energy-saving operation speed of metro based on APSO

YANG Hui1, 2, LI Ying1, 2, ZHOU Yanli1, 2

(1. School of Electrical and Automation, East China Jiaotong University, Nanchang 330013, China;2. Key Laboratory of Advanced Control and Optimization of Jiangxi Province, Nanchang 330013, China)

In the current research on energy-saving operation optimization of multi-station between urban rail trains, the traction energy consumption model does not consider the actual operating state, and is determined only by two indicators of train control force and running speed, and the fixed operation mode is widely adopted, which is difficult to dynamically adjust according to the actual environment. According to the actual running process of the train, this paper firstly studied the influence of running time and inter-station distance on the running energy consumption, analyzed the energy-saving operating conditions of the distance between the same station, studied the conversion sequence of working conditions, and then reconstructed the energy optimization model. Finally, the improved particle swarm optimization algorithm was used to solve the working condition transition point to realize the energy saving optimization of the train speed curve. The simulation results show that the contrast accuracy of the reconstructed energy optimization model and the traditional model is improved by 1.16%, and the optimized operating energy consumption is 6.92% lower than the original fixed driving strategy, which has better energy saving effect.

urban rail train; traction energy consumption; speed optimization; working condition conversion; improved particle swarm algorithm

U29-3

A

1672 − 7029(2020)08 −1926 − 09

10.19713/j.cnki.43−1423/u.T20191059

2019−11−29

国家自然科学基金资助项目(61673172，61663013，61803155)

杨辉(1965−)，男，江西高安人，教授，博士，从事复杂工业过程建模、控制与优化，轨道交通自动化与运行优化的研究；E−mail：yhshuo@263.net

(编辑 蒋学东)