基于阻尼力的二维桥式吊车模糊PID 控制器设计

王天雷，邱炯智，张宪文，郝晓曦，张京玲，吴惠翠

（1.五邑大学 智能制造学部，广东 江门 529020；2.恩平帕思高电子科技有限公司，广东 恩平 529499）

桥式吊车控制系统在建模过程中大多忽略了空气阻力、摩擦力等外部阻尼力，使得模型不准确，仿真与实际性能差异较大. 文献[1]提出了一种针对桥式吊车的简单的线性风力模型，风力参数的大小与迎风面积有关. 文献[2]设计了一个模拟器，用来预测和模拟风力，并对风力干扰进行补偿. 文献[3]针对二维桥式吊车系统考虑二维风力干扰，在不同方向上分别采用余弦和正弦风力模型. 然而，上述方法建立的模型要么过于简单与实际情况差异较大，要么信号结构复杂、耦合性高，难以用于桥式吊车实际控制器设计.

在桥式吊车控制器设计方面，滑模变结构控制[4]和PID（Proportional integral derivative，比例积分微分）控制[5]技术被广泛应用，然而滑模控制器需要精确的系统模型，且存在着高能耗与强抖振问题. 与之相比PID 性能较稳定，结构简单易实现. 但传统的PID 控制过分依赖参数的选取，人工参数整定需要操作者具有丰富的经验，自动整定方面采用的以粒子群算法[6]、神经网络算法[7]为代表的方法多为离线寻优，较难满足工程实践要求.

针对上述问题，本文在动力学建模过程中考虑复杂环境下的空气阻力与摩擦力，建立了一种新型的二维桥式吊车系统模型；并在此基础上设计模糊自适应PID 控制器，应用于二维桥式吊车系统的防摆定位控制.

1 桥式吊车数学模型

如图1 所示，二维桥式吊车是一种欠驱动的非线性系统动力学模型. 吊车M、荷载m 与钢丝绳l 连接，吊车的运动会引起荷载的摆动，荷载运动的角度（钢丝绳与垂直方向的夹角）表示为θ. 水平驱动力F 使吊车在x 方向上水平移动，钢丝绳的拉力Fl使载荷上升. 吊车与导轨之间的摩擦力为f，吊车与负载运动过程中所受空气阻力分别表示为Fw和Fθ.

本文利用拉格朗日方程求得桥式吊车系统动力方程：

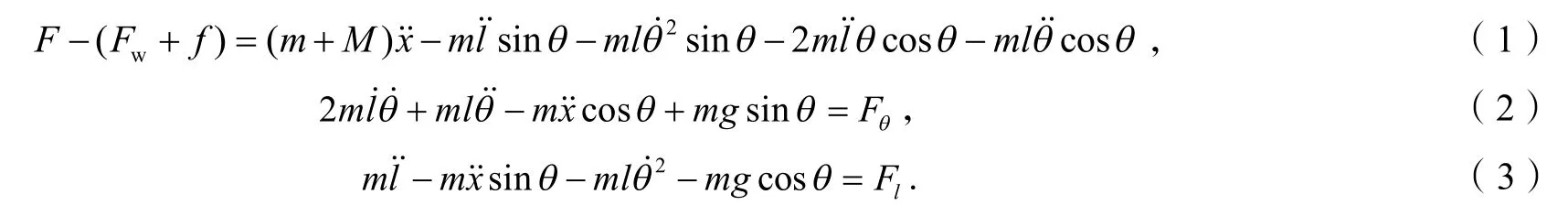
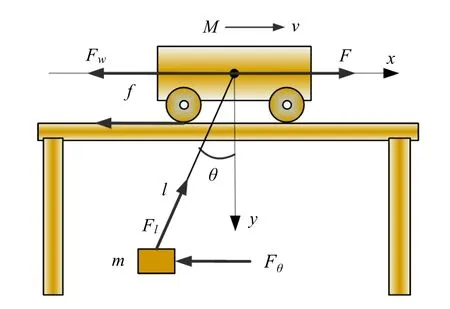
图1 桥式吊车模型

为了使所建桥式吊车系统动力学方程更符合实际工程情况，本文在模型建立过程中充分考虑系统的摩擦阻力和空气阻力，并对模型进行改进.

1）摩擦力模型. 在工作过程中，桥式吊车与轨道之间的摩擦力客观存在，且其大小与吊车运动速度等因素有关，采用如下摩擦力模型[8]：

式中，fr0、σ、kr均为摩擦系数.

2）空气阻力模型. 运动物体空气阻力的方向与其运动方向相反，大小与其速度、空气密度、物体几何形状、体积等因素有关[9]. 实际应用中，为避免负载摆角过大发生事故，桥式吊车通常低速运行. 因此，本文采用低速运动空气阻力模型：

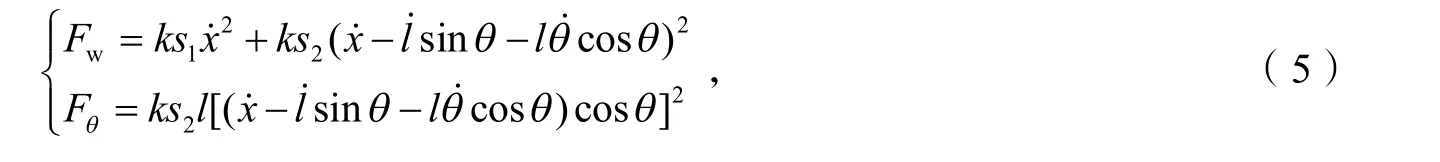
式中，s1,s2分别表示吊车运动方向的迎风面积和负载运动方向的迎风面积.

由式（1～5）可得包含空气阻力和摩擦阻力的二维桥式吊车系统动力方程：

2 控制系统设计

2.1 模糊自适应PID 控制器原理

PID 控制器常用于吊车的防摆控制，其基本结构如下：

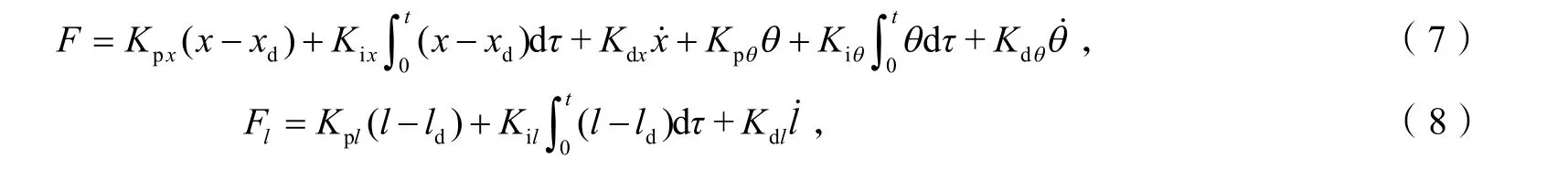
式中，xd,ld为小车位移及绳长的期望值，Kpq,Kiq,Kdq均为正常数.

由于控制的参数依赖主观经验，导致控制的效果无法达到最佳，因此衍生出模糊自适应PID 控制. 该控制器是以系统偏差e 和偏差变化率ec 作为输入量，用模糊控制器实时调整PID 控制器的控制量，进而实现控制的实时性和精确性，消除由普通 PID 控制器产生的超调和振荡的现象. 控制原理见图2.

由图2 可知模糊自适应PID 控制器的具体工作原理：以系统误差e 及其变化率ec 作为输入，利用模糊控制规则进行模糊推理，在线对PID 参数Kp、Ki、Kd进行调整，使其满足不同时刻的e 及ec 对PID 参数自整定的要求.

2.2 模糊自适应PID 控制器设计

根据桥式吊车防摆系统模型分析可知，系统应包含2 个PID 控制器，分别用于控制小车的位置及负载的摆角，控制器各变量的取值见表1.

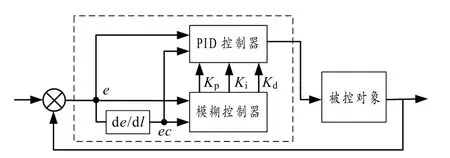
图2 模糊自适应PID 控制器原理图

表1 模糊自适应PID 控制器设计表

根据经验归纳法及操作系统的测量生成控制规则相结合的方法[10]，可得如表2 所示的对应的模糊控制规则. 模糊控制规则在Simulink 中生成的位置模糊特性曲面和摆角模糊特性曲面如图3 和图4 所示.

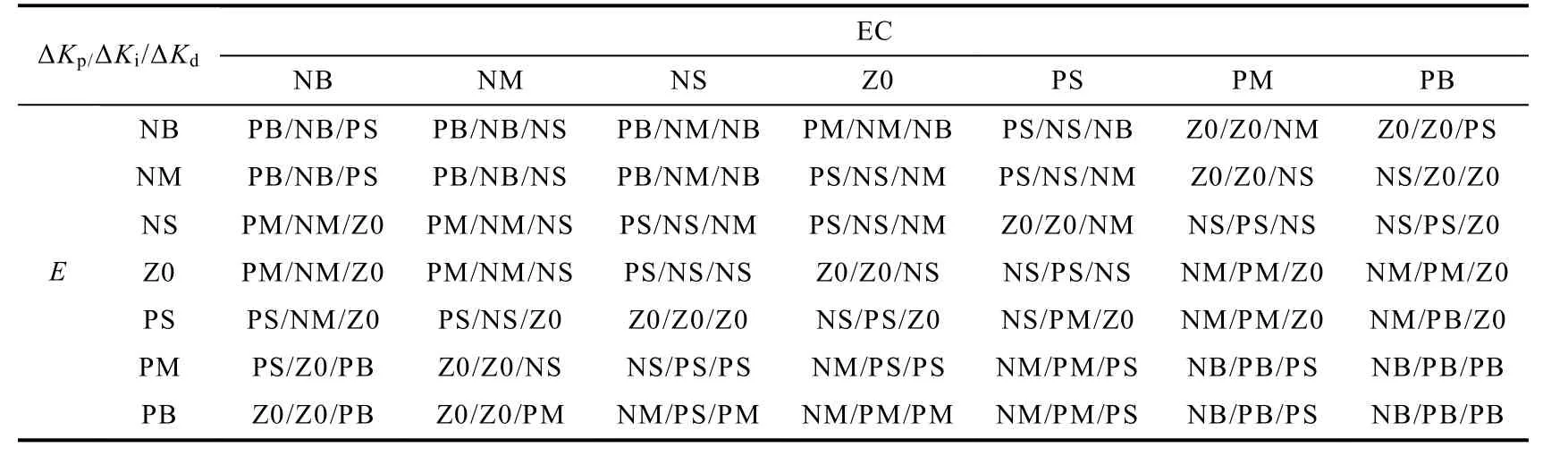
表2 ΔKp 、ΔKi 、ΔKd 的模糊控制规则表

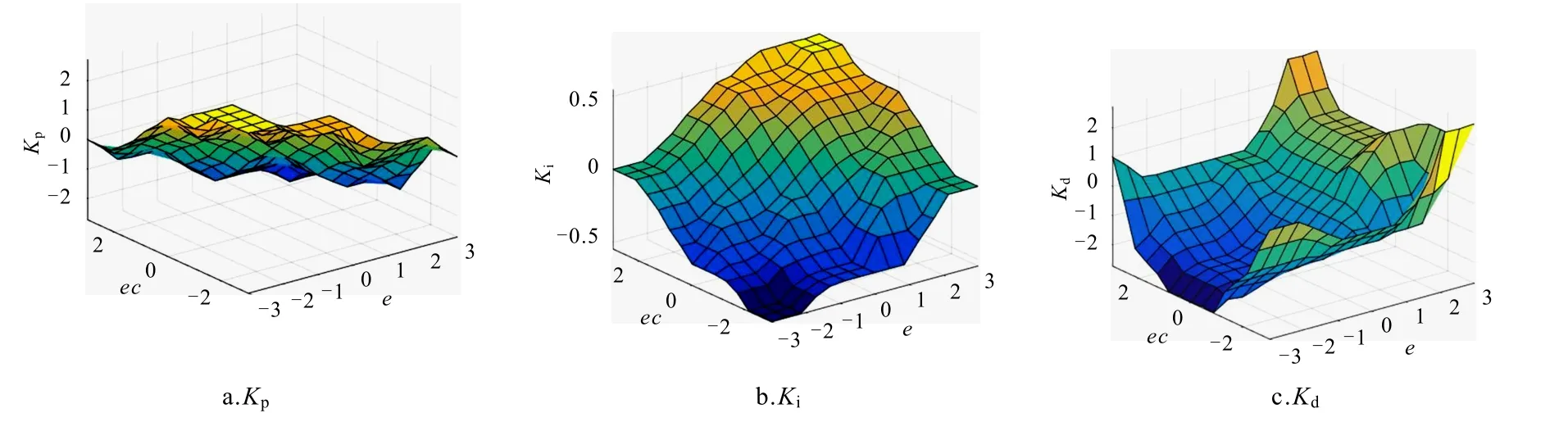
图3 位置模糊推理输出特性曲面

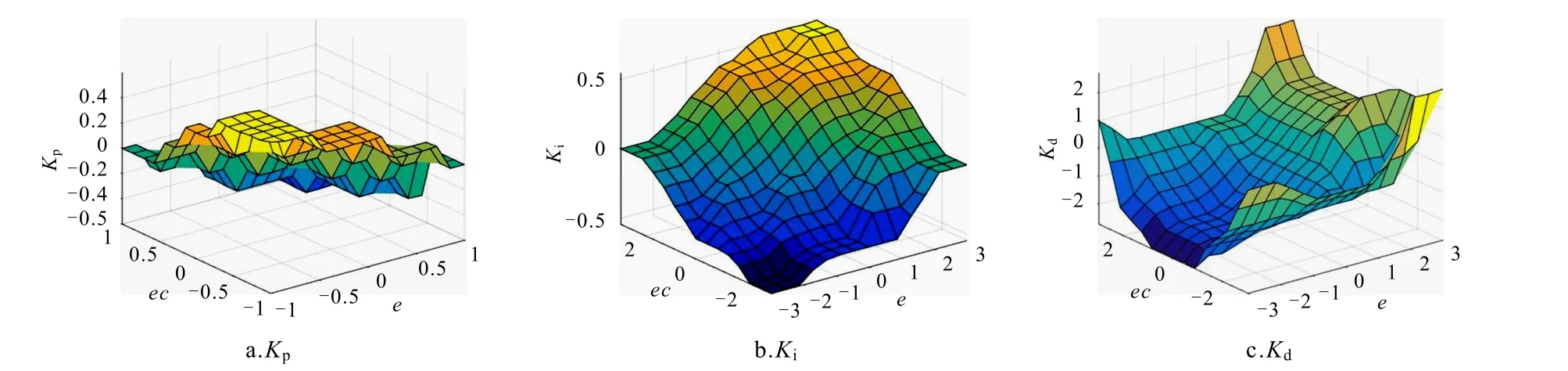
图4 摆角模糊推理输出特性曲面

由模糊控制得到的PID 控制器的3 个参数的修正量，通过式（9）即可获得具有实时性的控制参数，将所得参数用于控制器（7）及（8）中可得更好的控制结果.

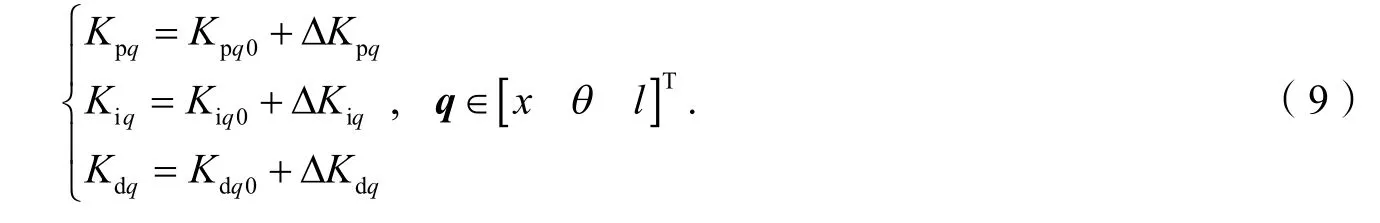
3 仿真实验与分析

为验证所提模型及控制器的有效性，采用 MATLAB/Simulink 对桥式吊车模型及其控制算法进行仿真. 为使仿真结果更接近实际工况，选取模型参数列入表3.

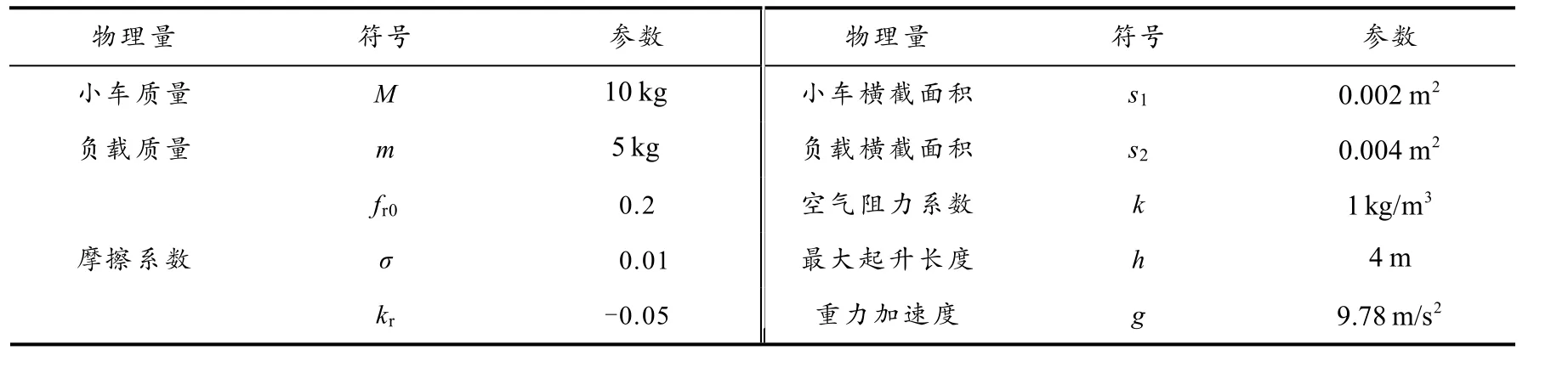
表3 桥式吊车参数

3.1 防摆控制仿真实验

将本文设计的控制器与 PID 控制、文献[11]中的多滑模控制进行仿真实验与对比分析. 为方便论文叙述，在此简述该多滑模控制器，其结构如下：

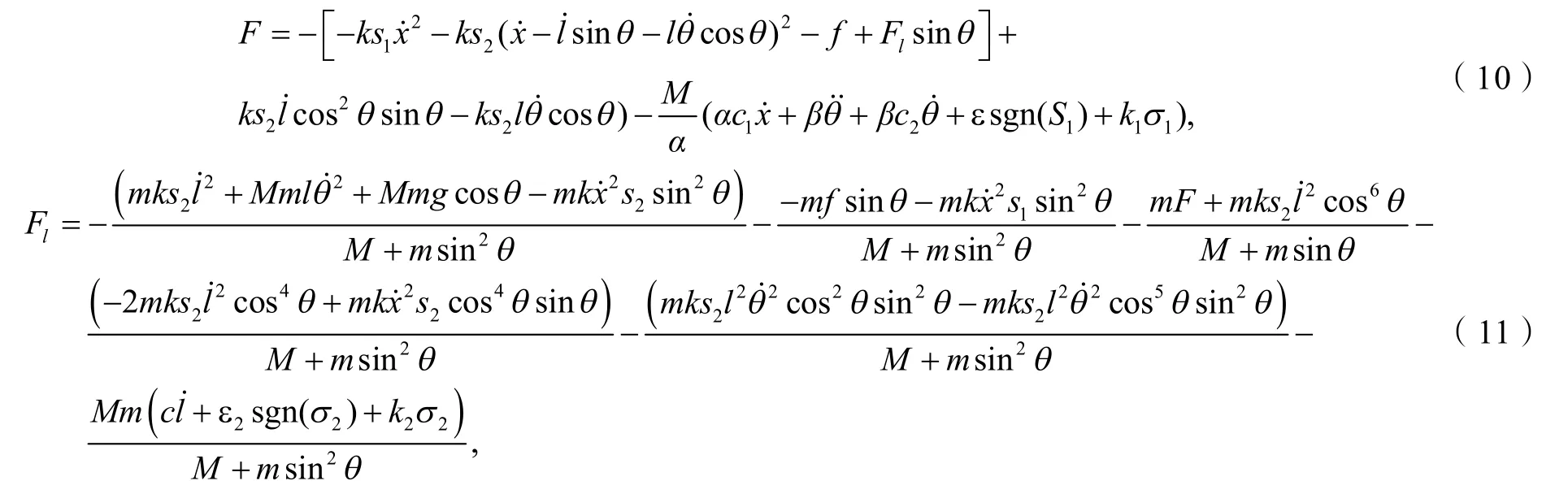
式中，xd,ld为小车位移及绳长的参考值，其与α,β,c1,c2,c3,ε1,ε2,k1,k2均为正常数. σ1和σ2分别代表桥式系统的位置滑动面和绳长滑动面，其定义详见文献[11]. 3 种控制器的参数设置见表4.

表4 3 种控制器参数设置

根据上述参数设计PID、模糊自适应PID 和多滑模变结构控制器，仿真框图如图5 所示，得到3 组位置、摆角和绳长变化曲线，如图6 所示.

由图6 可看出：1）图6-a 中，3 种控制器的控制位移曲线效果相近，其中模糊PID 控制器与PID控制器的收敛时间相近，均在10 s 左右即稳定收敛于目标值，滑模变结构控制的位移到达时间为14 s；2）图6-b 中，3 种算法对摆角的控制效果有明显的差异，虽在15 s 左右均达到稳定，但PID 控制器和多滑模控制器控制下的负载最大摆动角度分别为3.5°和2.3°，而模糊PID 控制下负载的最大摆角为1.6°，相比PID 控制及多滑模控制有较大的优势；3）图6-c 中，对于绳长的控制，由于仿真是由3 m 到4 m 的过程，所以其控制时间较短，PID 与模糊PID控制器收敛时间为3 s，多滑模控制的收敛时间仅为1s，但这可能要求电机输出较大功率.

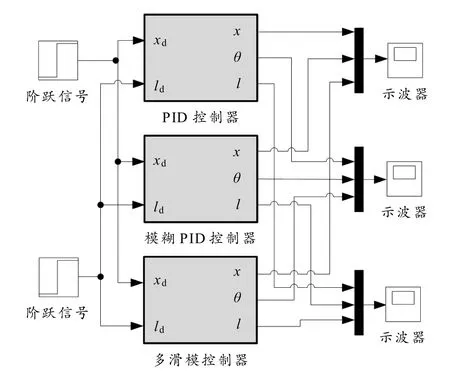
图5 桥式吊车仿真模型图

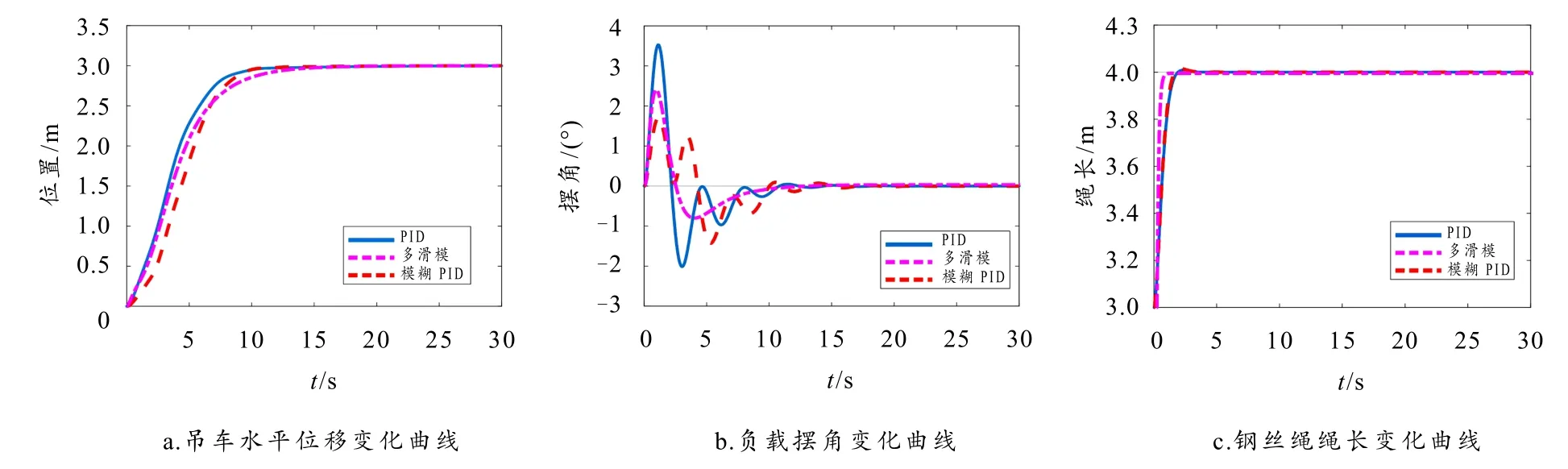
图6 桥式吊车防摆控制仿真曲线

3.2 鲁棒性实验

桥式吊车工作环境复杂，因此要求控制器对于外界扰动具有较强的鲁棒性. 为测试上述3 种控制器的抗干扰能力，在系统运行20 s 后（此时系统在稳定收敛状态），外界对负载施加瞬时扰动，使负载摆角增加0.5°，各算法控制结果如图7 所示.

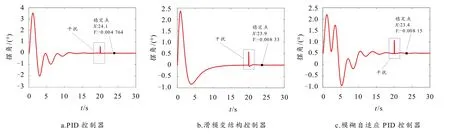
图7 桥式吊车抗扰动控制仿真曲线

由图7 可以看出，在第20 s 增加了约0.5°扰动后，吊车负载摆角在3 个控制器的控制下产生不同程度的抖动，并在有限时间内先后重新收敛于0. 其中，模糊PID 控制器在3.4 s 内即可恢复到平衡状态，而PID 控制器和滑模变结构控制器所花费时间分别为4.1s 和3.9 s. 结果表明本文设计的模糊PID 控制器比其他2 种控制器具有更好的鲁棒性.

4 结论

针对复杂工作环境下桥式吊车系统防摆控制问题，本文提出了一种基于阻尼力的二维桥式吊车系统模型，同时提出模糊自适应PID 控制器应用于该模型的防摆定位控制. 通过与PID、多滑模控制器的仿真结果比较发现，模糊自适应PID 控制器具有较好的防摆定位能力并且拥有对外界扰动较强的鲁棒性，有望应用于实际提高起重机的生产效率，同时复杂环境下的建模方法可以拓展应用到其他复杂环境下的欠驱动系统. 该控制器目前仅做了仿真实验，下一步将依托实物实验平台进行后续的研究工作.