基于稀疏分析的织物缺陷检测方法

李澄非，潘海欣，吉登清，蔡嘉伦

（五邑大学 智能制造学部，广东 江门 529020）

随着工业技术的快速发展，机器视觉技术被广泛应用并取代人工检测来完成对产品表面的缺陷检测任务[1-5]. 目前针对被测表面颜色单一，不存在复杂纹理的非模式背景图像，机器视觉技术的检测效果较好[6-7]. 但在模式背景图像中，由于该类图像中存在复杂的图案、轮廓、颜色或纹理干扰，同时缺陷目标会淹没在复杂的背景之中，对缺陷检测造成极大的干扰，大大增加了检测的难度[8-11].

织物表面图像就是模式背景图像，传统的织物表面缺陷检测主要依赖人工完成，存在效率低、成本高、漏检率高且无法持续工作等缺点. 近年来，越来越多的专家学者致力于运用机器视觉技术和智能算法实现织物缺陷的自动快速检测. 马丽萍[12]提出一种基于频谱特征分析的方法用于检测汽车安全带表面的缺陷，通过频域分析检测，误检率小于5%，漏检率小于3%，但该方法通用性不高，只能检测比较明显的缺陷图像. 景军锋等[13]提出一种基于卷积神经网络的织物表面缺陷检测方法，该方法通过Alexnet 网络实现对缺陷的特征提取并分类，最终可达到95%以上的分类准确率，且适用于多种缺陷. 该方法需要大量的样本作为训练集，不适用于小样本的检测. 因此，本文提出一种基于稀疏分析的纹理表面缺陷检测（Sparse Analysis Defect Detection，SADD）方法，从缺陷图像中去除背景，将缺陷从复杂的背景中提取出来，从而实现缺陷检测.

1 稀疏表示理论

织物表面图像具有重复的纹理背景的特性，如图1 所示，由于光照条件、相机分辨率等原因，各幅图像的灰度值、光照均匀度和图像对比度有着很大的差别，背景纹理严重地影响了图中缺陷的检测识别. 通过纹理图像的稀疏表示，可以将时域中复杂的纹理图像转化为简单有效的描述，进而实现纹理的分类.

1.1 信号的稀疏表示

稀疏表示[14-16]就是一种分解原始信号的过程，该过程通过字典将原始信号表示为字典元素的一个线性组合过程，公式如下：

图1 具有纹理分布的织物缺陷图像

其中y 为原始信号，A 表示字典，x 表示在字典上原始信号的表达，字典矩阵 A∈ Rm×n(m ≪n)，向量 x∈ Rn, y∈Rm. 假设字典是完备且冗余的，那么表达原始信号的线性组合将是不唯一的. 求解具有最少系数的最优表达即为求解该信号最稀疏表示的过程.

对任意的信号 y∈Rm，要想求得最稀疏的解，等价于解决下列问题：给定m 维空间中一组过完备 的 基 A∈Rm×n，选择最少个数的基向量，重构给定向量y，其定义如下：

求解公式（1）中非零个数最少的解即为求解稀疏解的过程，事实上这个问题是多项式复杂程度的非确定性问题（Non-deterministic Polynomial，NP）.

1.2 稀疏分解算法

正交匹配追踪算法（Orthogonal Matching Pursuit，OMP）得以解决上述的问题. 假设t 表示迭代次数，rt表示残差，表示t 次迭代后矩阵A 的原子索引集合，λt表示第t 次迭代得到的原子索引号，aj表示第j 个原子，即矩阵的第j 列，At表示由 Λt选出的矩阵A 的原子集合，大小为m × t的矩阵，xt为 t× 1的列向量. 输入为原始信号y，字典矩阵A，稀疏度k，输出为信号稀疏表示系数则OMP 算法流程图如图2 所示.

匹配追踪算法在算法过程中需要进行大量的内积运算，计算量巨大.为了更好地解决信号稀疏表示和分解的问题，Donoho 等又提出了基追踪（BP）算法. 算法原理是要找到一种信号的表示，把(0P)的问题转化为(1P)的问题，即把最小化 l0范数转化为最小化1l 范数，从而将组合优化问题转化为凸优化问题：

BP 算法的推广就是基追踪去噪算法，把(1P)的问题变成无约束优化问题，(1P)λ 具有二次规划结构，可以通过许多方法进行求解.

近年来的研究表明，在信号稀疏精确重构中，字典的冗余性会影响线性表示的唯一性，但是如果字典是非相关的，仍然可以实现y 在A 下被充分稀疏的线性表出，同时通过相关算法求解出稀疏表示系数，实现原信号y 的精确重构.

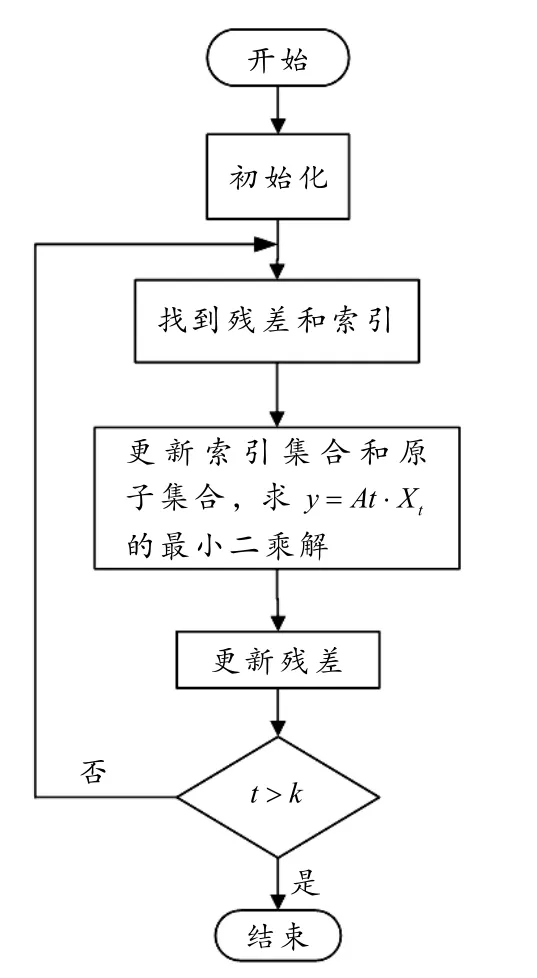
图2 OMP 算法流程图

2 缺陷检测的稀疏分析算法

2.1 缺陷图像稀疏表示模型

对于具有纹理分布的模式图像的表面缺陷检测而言，可以把缺陷图像Y 看成是纹理背景部分 Yt和缺陷前景部分 Yd的线性叠加组成的：

通过稀疏表示方法，可以将缺陷从纹理背景中分离出来. 给定大小为N ×N 的图像Y ，纹理背景Yt仅包含缺陷图像的规则纹理部分，假设存在一个超完备字典，其中L 表示字典的原子个数，通常 L ≪N2，则对纹理背景进行超完备变换可以表示为：

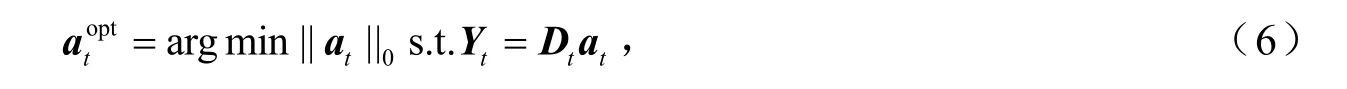
式（6）可求解一个稀疏的解，使得稀疏系数 at稀疏性最大.

对于缺陷前景部分 Yd，假设存在一个超完备字典，其中K 表示字典的原子个数，通常 K≪N2，使得求解下列问题：

同理，它也能够获得一个非常稀疏的解.

假设对于纹理背景项 Yt，缺陷字典 Dd不能得到一个稀疏解；对于缺陷前景项 Yd，在背景字典 Dt下也不能产生稀疏解. 根据上述假设条件，缺陷图像Y 的稀疏表示可以用以下模型来表述：

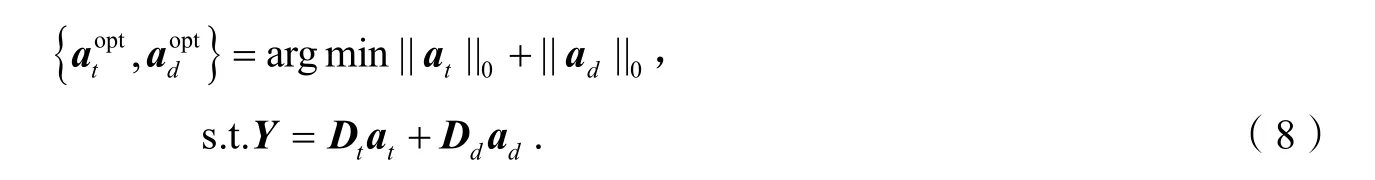
在实际应用中，由于噪声的干扰，缺陷图像不可能完全分解为缺陷前景图像和纹理背景图像. 因此式（8）的模型可以转换为：

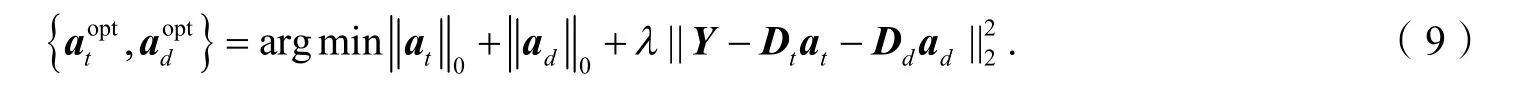
由于缺陷图像的稀疏分解是一个近似过程，第三项为重构图像与原始图像之间的误差，它在一定程度上表征了图像的噪声. λ 为权重系数. 然而根据MP 算法和BP 算法的思想，上述模型又可以转换为：

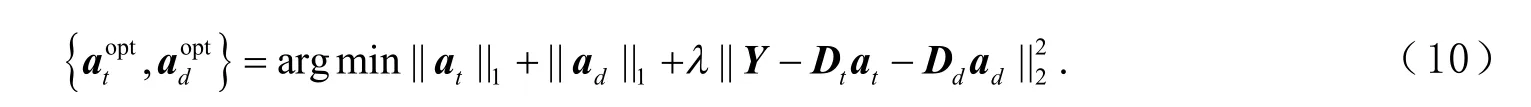
定义 D+=DT(DDT)-1是字典D 的Moore-Penrose 伪逆. 若给定 Yt，则其中 rt表示字典 Dt的零空间的任一向量，代入式（10）可得：

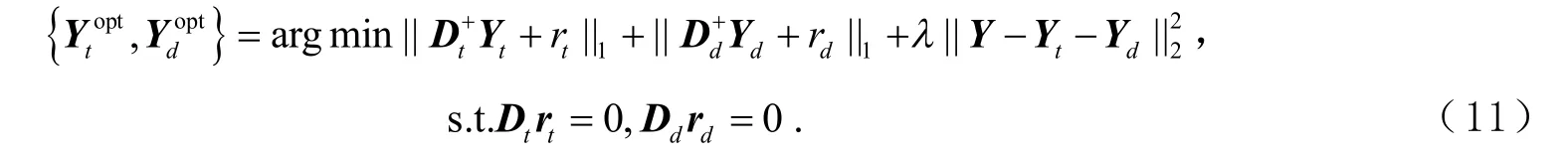
为了简化计算，设置 rt=0, rd=0，则模型可简化为：

求解式（12）的缺陷图像的稀疏表示模型，就可以得到最优解

2.2 基于稀疏分析的缺陷检测算法SADD

结合块坐标松弛方法的原理，通过交替优化的方法可以计算得到和. SADD 算法流程图如图3 所示，算法步骤如下：

1）初始化：缺陷图像Y 、纹理背景字典 Dt、缺陷前景字典 Dd、迭代次数J 、系数向量的最大长度 Lmax、权重系数λ；

2）计算阈值： δ=λLmax；

3）循环执行：

a. 假设 Yt不变，更新 Yd，计算残差R，R=Y-Yt；计算根据阈值δ 来筛选，得到系数；通过重构 Yd；

b. 假设 Yd不变，更新 Yt，计算残差R，R=Y-Yd；计算根据阈值δ 筛选，得到系数；通过重构 Yt；

c. 更新阈值δ=δ-λ ；

d. 如果δ ＞λ 转至步骤3），否则结束.

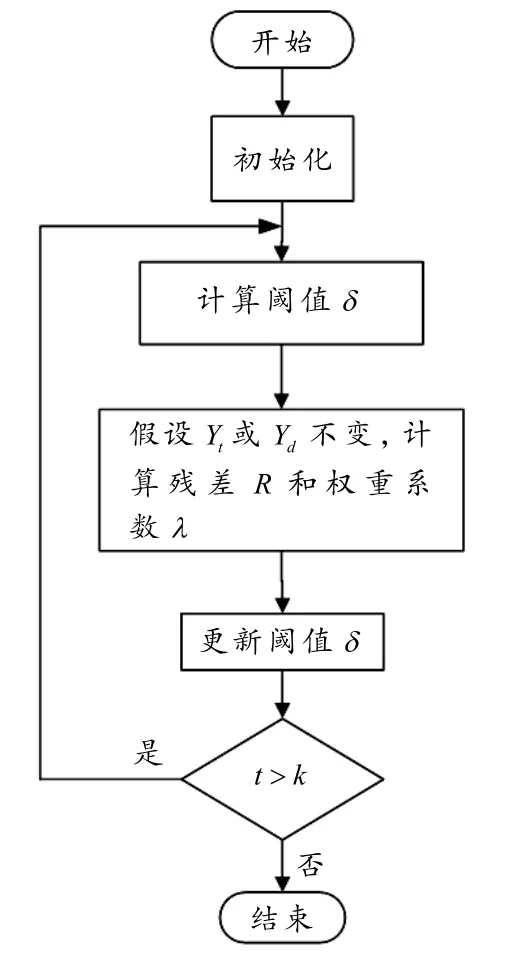
图3 SADD 算法流程图

2.3 字典的选择

在上述缺陷检测算法中，选择合适的字典 tD 和 dD 至关重要. 合适的字典能实现对信号中特定的成分的有效稀疏表示. 字典选择的规则是要求每一个字典都可以对其所表示的信号进行稀疏表示，且每个字典互不相关.

在本算法的模式背景图像缺陷检测中，由于缺陷图像的背景具有规则的纹理，在SADD 算法中选择LDCT 作为背景字典，选择Curvelet 变换作为缺陷字典. 对于大小为n ×n 的图像，Curvelet 变换的算法复杂度为 O(n2log2n)，LDCT 的算法复杂度也是 O(n2log2n). 因此SADD 算法总的复杂度也就是 O(n2log2n).

3 实验结果与分析

织物图像具有高度纹理特征，无缺陷织物表面纹理排列会呈现出很高的规则度与一致性. 当有缺陷出现时，正常织物纹理的局部周期性会被破坏. 以多种类织物表面缺陷图像为检测对象，验证SADD 算法对纹理模式图像缺陷检测的有效性，同时对比其他检测方法的结果. 图 4 所示为采用SADD 算法对大小为256 ×256的织物缺陷样本进行缺陷提取和分割的结果. SADD 算法经过数次迭代运算后，能够很好将缺陷前景从纹理背景中分离出来，缺陷前景得到了显著性的增强，从而将模式背景图像的缺陷检测转换为非模式图像的检测. 为了更清晰地显示缺陷检测的结果，对缺陷前景图像进行滤波及二值化处理.

图4 SADD 算法缺陷检测结果

在工业检测应用中，算法的运算速度也是关键的性能指标. 在SSAD 算法中，一个重要的参数就是迭代次数J . 迭代的次数J 越大，算法收敛得越慢，运算时间越长. 但是J 越小，缺陷提取的效果越差，甚至可能会出现漏检或误检. 待检测图像尺寸越大或者背景图像越复杂，所需的迭代次数J越大. 对于同一产品在不同的环境下采集的图像，SSAD 算法的收敛速度有所不同，因此J 的选择也不同. 通过离线学习可以得到一个最佳的经验值，根据不同的情况选择不同的经验值. 在织物的缺陷检测中，SADD 算法最多迭代到 15 次就会收敛，缺陷前景图像和纹理背景图像保持稳定不变，并且能够很好地进行缺陷分割和提取.

为了进一步验证 SADD 缺陷检测算法的有效性，选取4 类织物表面缺陷图像共400 张作为测试数据集进行缺陷检测实验. 该数据集中包括100 个缺陷样本和300 个无缺陷样本. 测试实验同时用本文的方法与文献[8]算法进行结果对比，以漏检率、误判率和检测正确率作为缺陷检测技术的性能指标. 检测结果数据如表1 所示，部分产品样本检测结果如图5 所示.

表1 两种方法的检测结果对比

图5 多种织物缺陷检测结果对比

从表1 看出，文献[8]提出的算法对测试集的漏检率为7%，但是误检率却达到20.3%，说明该方法针对模式背景图像的检测能力很低，容易将部分图像检测为包含缺陷的图像，而本文提出的检测方法漏检率为5%，误检率为2.7%. 由图5 可以看出，针对同一张缺陷图像，文献[8]的方法无法准确分割出缺陷，容易产生误判区域，SADD 算法的分割精度相对精准. 本文实验的硬件平台为Inter Core i7-8700M、3.19 GHz 和8 Gb 内存CPU，利用HALCON18.0 完成相关检测实验，其中本文算法平均处理一幅图像的时间为0.47 s. 由此可得，本文提出的检测方法针对具有复杂纹理的模式背景图像，具有一定优越性.

4 结论

本文提出了一种基于稀疏分析的SADD 算法，用于检测具有纹理背景的模式图像. 对于具有不同纹理背景的织物产品的检测，当纹理背景具有一定的周期性或一致性时，使用本文提出的SADD算法均能取得较好的缺陷提取效果，且该算法对不同分辨率、不同光照条件及不同缺陷类型的图像都具有较好的鲁棒性. 但对于背景纹理规律性较差的图像，SADD 算法并不能很好的把缺陷部分从背景中分离出来. 当背景纹理的一致性不强时，SADD 算法对该背景图像地重构效果不佳，前景图像中的背景部分并没有去掉，缺陷区域没有凸显出来，几乎完全融入了背景纹理中，无法利用SADD算法来对其进行分割. 因此缺陷提取过程中，缺陷区域没有提取完整，把部分背景当作了缺陷，导致出现误检. 针对该问题，今后将尝试采用深度学习中端到端的检测框架对缺陷区域进行更精准的检测和定位.