基于频率法的理论计算吊杆索力研究

艾玉麒，黄方林，冯帆，黄启宣

基于频率法的理论计算吊杆索力研究

艾玉麒，黄方林，冯帆，黄启宣

(中南大学 土木工程学院，湖南 长沙 410075)

为提高工程中吊杆索力计算精度，引入系杆拱桥吊杆一端铰支一端固支的边界条件，并考虑叉耳对吊杆振动的影响，采用能量法推导出吊杆索力和吊杆自振频率之间的显式表达式。在此基础上，进一步推导出考虑温度影响的吊杆索力和自振频率之间的显式表达式，依据温度修正计算吊杆索力值，并与设计索力值对比。以新城大桥为实例，利用本文方法与传统方法进行计算，并与大桥实测索力进行比较，本文方法计算结果与实测值更为接近；且采用本文考虑温度影响的计算式二次计算索力后，结果表明吊杆索力值随温度降低而增大。研究结果表明：采用本文方法计算吊杆索力能提高计算精度。

系杆拱桥；边界条件；吊杆索力；频率；温度

对于中、下承式系杆拱桥，吊杆是其关键组成部分，桥面和主梁由吊杆支承，吊杆将上部结构自重与活荷载传递给拱肋。吊杆在施工过程中和成桥后起着控制桥梁几何形状和构件线形的重要作用，因此必须对其受力进行监测，以避免桥梁产生过大应力，且吊杆索力测量的准确与否直接关系到整桥的内力分布和线形控制。目前，索力测量方法主要有油压表法、压力传感器法、磁通量法和频率法 等[1−2]。上述几种方法中，以频率法最为经济、实用，因而应用最为广泛[3]。为确定吊杆索力和频率之间的关系，国内外许多学者进行了相应研究分析[4−6]，考虑吊杆的不同边界条件[8−9]、吊杆自身参数[10]、环境温度的变化[12−13]对吊杆索力的影响。现有研究中，一些吊杆索力计算式往往不能表达实际吊杆边界条件，且没有全面考虑吊杆自身参数，致使计算结果误差较大；一些吊杆索力计算方法需要实测吊杆边界条件的参数[14−15]，且在工程中这些参数不便测量；考虑温度对吊杆索力的影响时，仅考虑吊杆的热胀冷缩，未考虑拱肋和桥面系对吊杆约束的影响，将会导致计算结果不准确。针对以上问题，因考虑到大多数的中、下承式系杆拱桥中吊杆的边界条件可以简化为一端铰支一端固支(如吊杆上端固支于拱肋，下端铰支于钢梁)。为了能更好地模拟实际情况，本文采用频率法，从吊杆实际边界条件出发，引入一端铰支一端固支的边界条件。由于铰支端的叉耳质量较大，对于吊杆的振动影响不能忽略。推导出考虑叉耳对吊杆自振频率影响的吊杆索力计算式。在此基础上，推导消除温度影响的计算吊杆索力公式，通过新城大桥的实际试验结果验证了计算公式的有效性。

1 吊杆张力计算模型

振动法测试吊杆张力的理论基础是弦振动理论。考虑到中、下承式拱桥吊杆约束的特点，本文引入一端铰支一端固支的边界条件，并考虑到叉耳对吊杆自振频率的影响。本文将叉耳等效简化为长度为2的吊杆，具体模型图如图1所示。其中，1和2分别为吊杆和叉耳的抗弯惯性矩，1和2分别为吊杆和叉耳的长度。吊杆和叉耳的弹性模量为。

图1 吊杆计算模型图

2 系杆拱桥吊杆索力计算实用公式

2.1 叉耳对吊杆索力的影响

对于系杆拱桥来说，由于吊杆长度相对于拉索较短，斜度小，因此不用考虑吊杆斜度和垂度影响。由图1的吊杆计算模型，应用动力学普遍原理，可以建立其无阻尼自由振动方程[7]：

式中：为吊杆索力，假定其为常量；1()和2()分别为吊杆和叉耳的横向位移函数；1和2分别为吊杆和叉耳的抗弯刚度；1和2分别为吊杆和叉耳的线密度。

考虑到叉耳和吊杆之间的联系为固结，且叉耳长度远小于吊杆长度。因此可以近似处理两者的位移函数：

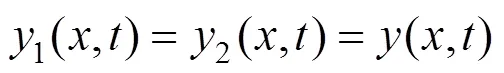
采用分离变量法，位移函数()可以用广义坐标()和形状函数()表示为：

由于式(1)为线性微分方程，其自由振动为简谐振动，可以解出：

吊杆振动的总动能为：

最大动能为：

吊杆振动的总势能为：

最大势能为：

根据吊杆端部的平衡条件，一端铰支一端固支的边界条件可以表述为：

一般情况下吊杆的净截面直径与计算长度之比很小，故不考虑剪切变形和转动惯量的影响。可以得到形状函数的一般形式：

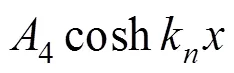
式中：1，2，3和4为待定系数，由吊杆边界条件确定。将边界条件代入上式计算，可得2=0，4=0，并有方程组：

因形状函数()不为0，则常系数1和3不全为0。由行列式为0得：

由上2式可得1和3关系并将此代入式(14)得出形状函数表达式：

由式(14)可得1=3.926 6(基频)。将形状函数()的解析式和基频代入式(13)可以得到：

整理上式得吊杆索力显式表达式：

当2=0时，即不考虑叉耳对吊杆振动的影响，可以得到与文献[9]相同的结果。

2.2 温度对吊杆索力的影响

吊杆材料受温度的变化而热胀冷缩，将会导致吊杆长度的变化，进而使吊杆振动频率发生变化，致使频率法计算公式得出的索力值与设计索力值差别较大。

在系杆拱桥的施工和检测中，吊杆索力的设计值是基于年平均温度时结构受力给定的。单根吊杆的索力受温度变化值为：

式中：Δ为索力变化量；为线膨胀系数；为横截面积；1为实时温度；为设计温度(年平均温度)。

创新政策举措。尊重群众意愿，把农村新型社区建设与改善低收入群众住房条件、建设美丽乡村和土地增减挂钩相结合，让低收入户、低保户等困难群众优先进入新型社区。今年上半年，全县新实施入库增减挂钩项目5537亩，占补平衡项目2900亩。

在实际情况下，吊杆索力的变化受到拱肋和横梁及其他吊杆的约束，其索力变化量应该为：

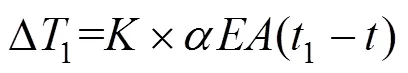
为温度修正系数，由相应的有限元模型计算得到。实时温度下对应的设计索力1为：

由式(17)，(19)和(20)可以得到实时温度下对应的设计索力1为：

3 实例验证

3.1 工程概况

新城大桥主桥采用(36+148+36) m飞燕式钢箱系杆拱桥结构形式，主桥全长220 m。拱肋矢高37 m，矢跨比1/4，主、边拱肋均向桥轴中心线倾斜，倾角为76.826°，边拱肋两端之间设置系杆索，平衡拱肋推力。吊杆采用7 mm高强度镀锌钢丝，全桥共布置13对吊杆，吊杆沿桥纵向为垂直布置，标准间距为8 m，吊杆详细编号见图2。

图2 吊杆编号

全桥吊杆采用PESC7-73和PESC7-91 2种规格，HL1和 HR1吊杆型号为PESC7-91，其他吊杆型号为PESC7-73，吊杆的热膨胀系数为1.2× 10−5℃。因一侧的吊杆具有对称性，本文选取其左右幅共6根吊杆。选取吊杆的具体参数及实测频率如表1~2所示。

表1 吊杆参数表

表2 吊杆的实测频率

3.2 试验值和计算值对比

3.2.1 叉耳对吊杆索力的影响

为验证叉耳对吊杆索力的影响，将实测频率代入文献[8]、文献[9]及本文式(17)，计算得到的索力值分别与索力实测值作为对比，本文推导的考虑叉耳影响的实用索力计算公式设定为3，计算结果对比如图3和图4所示。

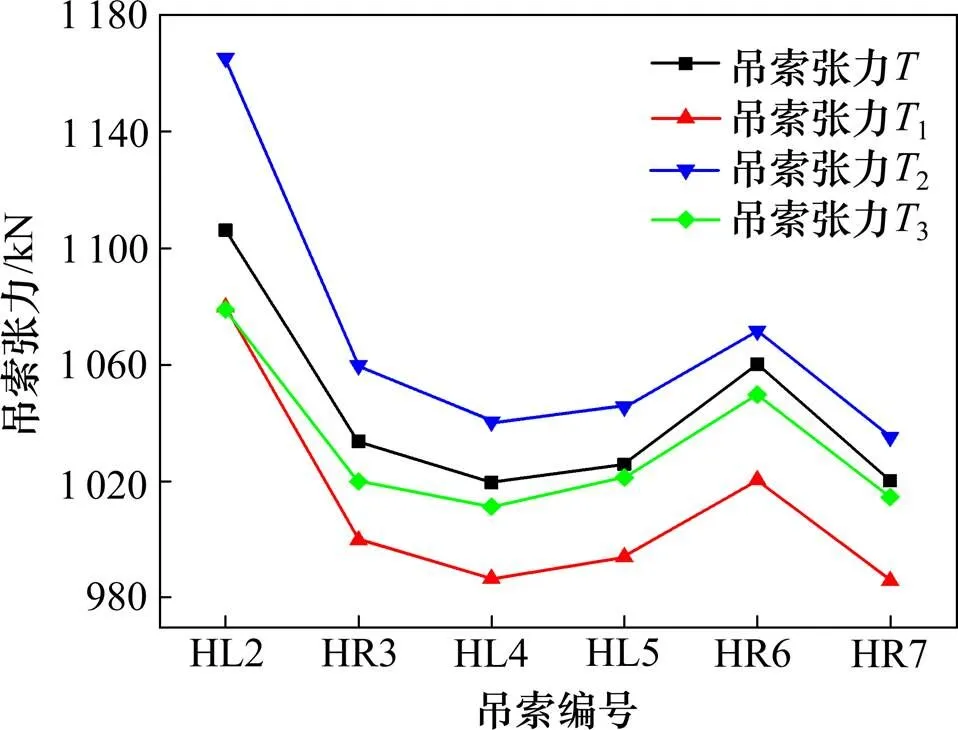
图3 吊杆索力

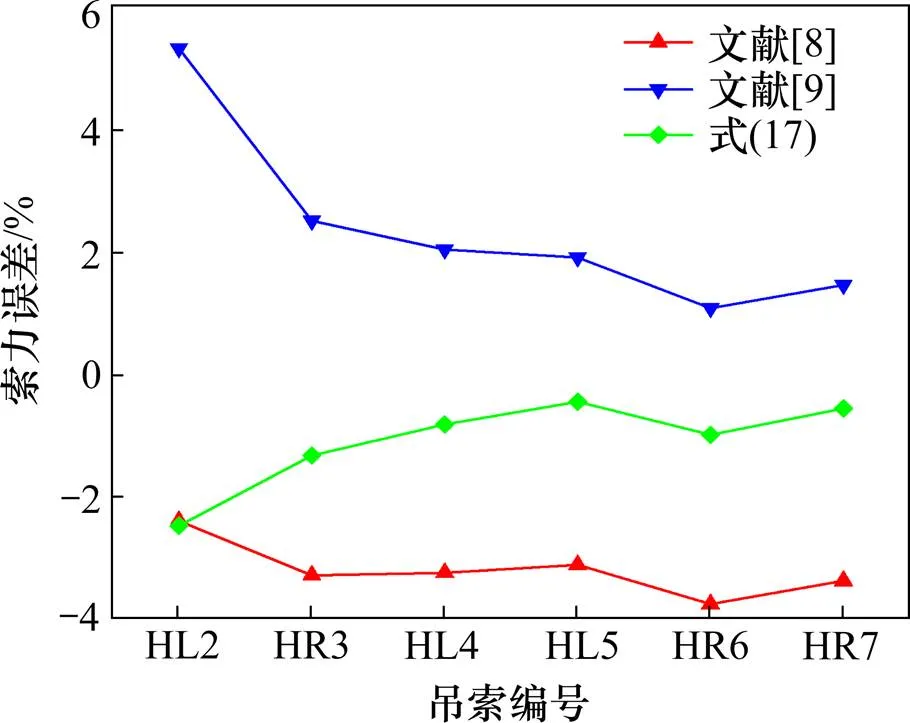
图4 索力误差

3.2.2 温度对吊杆索力的影响

新城大桥吊杆索力值对应设计温度为16 ℃，测量时温度为12 ℃，温差为4 ℃，用Δ表示。由工程软件计算得出温度修正系数，如表3所示。

表3 各杆的温度修正系数

为验证温度对吊杆索力的影响，将实测频率代入本文式(17)和本文式(21)，计算得到的索力值分别与索力设计值0对比，本文推导出的考虑温度影响的实用索力计算公式设定为4；不考虑温度影响的吊杆索力用3(同上)表示；25 ℃季温影响下用4j表示。计算结果对比和误差如图5和图6所示；在25 ℃季温影响下索力计算结果对比如图7所示。

图5 考虑温度的吊杆索力

图6 考虑温度下的索力误差

由图5和图6可以得到，在吊杆其他条件不变的情况下，温度降低，索力大小呈上升的趋势。当实际温度比设计温度低4 ℃时，由本文式(21)得出的计算索力略低本文式(17)的计算索力4~10 kN。两者相比于设计值，考虑温度影响的索力计算值式(21)更接近设计索力，误差在4%以内。

由图7可得，若考虑到25 ℃季温的影响，本文式(21)和本文式(17)的差值在25~64 kN范围内，占到自身索力的2%~6%。表明当温度变化较大的情况下，温度对于索力计算的影响不能忽略。

图7 季温影响下吊杆索力

4 结论

1) 本文方法考虑了系杆拱桥实际边界条件，由计算得出的索力与实际索力误差在2%以内，表明本文公式可以用于系杆拱桥吊杆索力的频率法 测量。

2) 当实测温度与年设计温度相差不大时，温度效应对于索力测量误差不大，如果温差大(如季温差)就需要考虑温度对索力的影响。

[1] 方志, 汪建群, 颜江平. 基于频率法的拉索及吊索张力测试[J]. 振动与冲击, 2007(9): 78−82, 171−172. FANG Zhi, WANG Jianqun, YAN Jiangping. The tension measurement of cables and suspenders with frequency method[J]. Journal of Vibration and Shock, 2007(9): 78− 82, 171−172.

[2] 宋杰, 陈鲁, 张其林. 磁通量法在预应力悬挂结构拉索施工中的应用[J]. 振动、测试与诊断, 2009, 29(1): 86− 91, 120−121. SONG Jie, CHEN Lu, ZHANG Qilin. Application of magneto-elastic method to tension measurement of prestressed cables in suspended structure[J]. Journal of Vibration, Measurement & Diagnosis 2009, 29(1): 86−91, 120−121.

[3] 王建飞. 拱桥吊杆索力的振动法测量[D]. 哈尔滨: 哈尔滨工业大学, 2012. WANG Jianfei. Vibration method measurement for cable tension of arch bridge[D]. Harbin: Harbin Institute of Technology, 2012.

[4] SHAN D, CHAI Y H, ZHOU X, et al. Tension identification of suspenders with supplemental dampers for through and half-through arch bridges under construction[J]. Journal of Structural Engineering, 2018, 145(3): 04018265.

[5] 魏建东. 索力测定常用公式精度分析[J]. 公路交通科技, 2004(2): 53−56. WEI Jiandong. Precision analysis of conventional formulas calculating cable tension[J]. Journal of Highway and Transportation Research and Development, 2004(2): 53−56.

[6] ZUI H. Practical formulas for estimation of cable tension by vibration method[J]. Journal of Structural Engineering, 1996, 122(6): 651−656.

[7] Clough R W, Penzien J. Dynamics of structure[M]. 2nd ed. California: Computers and Structures Inc, 1995: 120− 129.

[8] 陈淮, 董建华. 中、下承式拱桥吊索张力测定的振动法实用公式[J]. 中国公路学报, 2007(3): 66−70. CHEN Huai, DONG Jianhua. Practical formulae of vibration method for suspender tension measure on half-through and through arch bridge[J]. China Journal of Highway and Transport, 2007(3): 66−70.

[9] 孟少平, 杨睿, 王景全. 一类精确考虑抗弯刚度影响的系杆拱桥索力测量新公式[J]. 公路交通科技, 2008(6): 87−91, 98. MENG Shaoping, YANG Rui, WANG Jingquan. Novel fomula of tension measurement for tied arch bridge inprecise consideration of flexural rigidity[J]. Journal of Highway and Transportation Research and Development, 2008(6): 87−91, 98.

[10] 孙永明, 李惠. 端部性质对频率法测量竖直拉索索力影响分析[J]. 工程力学, 2013, 30(8): 10−17. SUN Yongming, LI Hui. Effect of extreme properties of vertical cable on the cable force measurement by frequency-based method[J]. Journal of Engineering Mechanics, 2013, 30(8): 10−17.

[11] 吉伯海, 程苗, 傅中秋. 基于振动频率法的斜拉桥索力测试影响因素[J]. 中南大学学报(自然科学版), 2015, 46(7): 2620−2625. JI Bohai, CHENG Miao, FU Zhongqiu. Influential factors in cable force measurement of cable-stayed bridges based on vibration frequency method[J]. Journal of Central South University (Science and Technology), 2015, 46(7): 2620−2625.

[12] 何伟, 朱亚飞, 何容. 环境温度对钢管混凝土拱桥吊杆振动影响及张力测定研究[J]. 地震工程与工程振动, 2016, 36(4): 217−225. HE Wei, ZHU Yafei, HE Rong. Ｒesearch on vibration properties of suspenders of concrete filled steeltube arch bridges affected by temperature and tension measuring methods[J]. Earthquake Engineering and Engineering Vibration, 2016, 36(4): 217−225.

[13] 周先雁, 王智丰, 冯新. 基于频率法的斜拉索索力测试研究[J]. 中南林业科技大学学报, 2009, 29(2): 102− 106. ZHOU Xianyan, WANG Zhifeng, FENG Xin. Cable tension measurement based on frequency method[J]. Journal of Central South University of Forestry & Technology, 2009, 29(2): 102−106.

[14] 何容, 何伟, 陈淮. 复合边界条件下基于能量法吊索张力实用公式[J]. 振动.测试与诊断, 2013, 33(2): 187− 191, 334. HE Rong, HE Wei, CHEN Huai. Practical formula for hanger tension under combined boundary conditions based on energy method[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(2): 187−191, 334.

[15] 张戎令, 杨子江, 朱学辉. 基于频率计算系杆拱桥吊杆张拉力的实用公式[J]. 西南交通大学学报, 2015, 50(5): 823−829. ZHANG Rongling, YANG Zijiang, ZHU Xuehui. Practical formulas to calculate suspender tension based on frequency[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 823−829.

Theoretical calculation of suspender tension based on frequency method

AI Yuqi, HUANG Fanglin, FENG Fan, HUANG Qixuan

(School of Civil Engineering, Central South University, Changsha 410075, China)

In order to improve the calculation accuracy of cable forces of suspenders in engineering, the boundary condition of one end hinged and one end fixed for the tied arch bridge is introduced, and the influence of the fork on the vibration is considered in this paper. The energy method was used to derive the explicit expression between the cable force of suspenders and the natural vibration frequency. On this basis, the explicit expression between the cable force and the natural frequency of the suspenders by considering the temperature influence was further derived, and the cable force of the suspenders was calculated according to the temperature correction, and compared with the design tension value. Taking the Xincheng Bridge as an example, the calculated results of this method are closer to the measured ones comparing with the traditional method. The results show that the cable forces increase with the decrease of temperature. The above results show that using this method to calculate the cable force of the boom can improve the calculation accuracy.

tied arch bridge; boundary conditions; suspenders force; natural frequency; temperature

U448.22；TH113

A

1672 − 7029(2020)08 − 2030 − 07

10.19713/j.cnki.43−1423/u.T20190935

2019−10−23

国家自然科学基金资助项目(51378504)

黄方林(1964−)，男，湖南邵东人，教授，博士，从事信号分析与处理、桥梁健康监测；E−mail：375339481@qq.com

(编辑 蒋学东)