基于时序卷积网络的情感识别算法
宋振振, 陈兰岚, 娄晓光
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
情感识别作为情感研究的核心内容能够使机器理解人的感性思维,影响着机器智能化的继续发展,成为影响人机自然交互的关键要素。同时,情感识别融合多学科为一体,其发展将会带动多学科的共同发展,其应用也会带来巨大的经济效益和社会效益,因此情感识别已成为研究的热点。
早期对人类情感的研究通常是利用人的面部表情[1]或人的声音信号[2]进行不同情感状态的识别,这两种人体信号虽然较易获得,但也十分容易被伪装,特别是当受试者不愿意被其他人察觉到自己的情感状态时。由于生理信号不易被伪装,因此有学者提出了利用人体生理信号,如脑电(Electroencephalogram,EEG)、心电、肌电、皮肤电阻、皮温、呼吸信号等来判断受试者的情感状态。Healey 等[3]的研究结果证明了应用生理信号进行情感状态辨别是可行的。在生理信号中,EEG 信号是一种比较敏感的客观指标,能够较为精确地反映出人的情感变化,因此近年来很多研究者开始使用EEG 信号进行情感识别。
深度学习是机器学习研究中的一个新领域,其目标在于建立、模拟人脑进行分析学习的神经网络,这种神经网络可以模仿人脑的机制来解释诸如图像、声音和文本等不同类型的数据。目前已有很多学者将深度学习应用于脑电情感识别。文献[4]使用深度置信网络(Deep Belief Network, DBNS)对EEG 信号进行二分类情感识别,识别精度能够达到86.08%;文献[5]结合卷积神经网络(Convolution Neural Network, CNN)和循环神经网络(Recurrent Neural Network, RNN)网络,对EEG 的正确识别率最高达到了74.12%;文献[6]提出了一种具有子节点的特殊神经网络对EEG 信号提取差分熵,最高正确率达到93.26%;文献[7]提出并评估了一套深度信念网络模型,并验证了这些模型对分类精度有很大的提高。
目前深度学习应用领域中的两大主流结构是CNN 和RNN。CNN 的特点之一是网络的状态仅依赖于输入,但它并不适用于所有问题。例如对于具有时间属性的数据而言,仅依靠当前时刻输入的效果并不是很理想,因此有研究者开始将序列模型用于情感识别的研究中。如文献[8]使用长短期记忆网络(Long Short-Term Memory,LSTM)对脑电信号进行情感识别,取得了很好的效果。然而,传统的序列模型都是在RNN 基础上的演变,如LSTM[9]、门控单元循环网络(Gate-Variants of Gated Recurrent Unit,GRU)[10]等,因此序列模型存在一个很大的问题就是它的训练效率相对于CNN 来说较低。因为RNN 的结构特点,使得每一个时刻的状态学习都依赖于前一个时刻的状态,因此无法做到并行运算,从而导致计算效率大大降低。此外,深度学习在训练模型过程中很容易陷入局部最优,很难得到全局最优值。针对以上问题,本文提出使用时序卷积网络(Temporal Convolution Networks,TCN)[11]对脑电信号进行情感识别,该模型既具有时间序列的特性同时也保留了CNN 的可并行计算特点,在保持精度的同时提高了计算效率。同时本文还采用Snapshot 快照集成策略[12],通过调整学习率的方式尽可能地寻找到最接近全局最优的值。
1 情感识别模型
基于脑电信号的情感识别步骤一般包括:情感的诱发、脑电信号采集、信号预处理、脑电特征提取及情感学习分类。
本文采用DEAP 数据集[13],使用TCN 模型进行情感识别,整体设计框架如图1 所示。首先采用小波包变换的方法对预处理过的原始数据提取特征,同时构建情感分类模型,为每个样本标注合适的情感标签;然后以TCN 模型为主体,使用Snapshot 优化训练方法选择出最优的情感识别分类器。

图1 基于脑电信号的情感识别算法总体框图Fig.1 Overall block diagram of EEG-based emotion recognition algorithm
2 数据集及预处理
2.1 DEAP 数据集
DEAP 数据集是由英国伦敦玛丽皇后大学的研究人员通过实验开发的一个用于分析人类情感状态的多模态数据集。该实验选取了40 段音乐视频(MV),每段音乐视频的时间长度为63 s,其中前3 s是准备时间。受试者在观看完每段视频后对该视频片段的效价、唤醒度、喜好程度和熟悉度等进行评分,分值为1~9。
该数据集记录了32 个受试者的40 个导联脑电生理信号。其中前32 个导联采集脑电信号,脑电电极的安放位置采用国际脑电图学会规定的10~20 系统电极放置法;后8 个导联采集人体的外围生理信号,包括眼电、肌电及皮肤电阻。本文仅使用了其中18名受试者的32 个导联脑电信号和受试者对每个视频片段的评价指标两部分数据。
2.2 数据预处理
数据经过预处理后最终得到每个受试者的数据格式为40 × 32 × 8 064,其中40 表示40 个视频片段,32 表示实验采用的导联数,8 064 表示对每个63 s 的视频片段以128 Hz 的频率进行采样,每个视频片段共采集得到63 × 128 = 8 064 个数据点。
3 情绪划分模型
TCN 模型是有监督学习模型,所处理的数据格式是有标签数据,而DEAP 数据集本身是没有标签的,所以在学习之前要给数据生成情感分类标签。在DEAP 数据集中,给数据生成情感分类标签主要是基于受试者对视频片段的评价指标,因此涉及到了情感的分类模型。
研究者通常从两种视角来建构和理解情感的分类模型:基本情感模型[14]和维度情感模型[15]。维度情感模型即情感状态的“愉悦度-唤醒度-支配度”三维模型[16]。Valence(愉悦度)表示积极或消极的情绪状态,如兴奋、爱、平静等积极情绪及羞愧、无趣、厌烦等消极情绪。Arousal(唤醒度)表示生理活动和心理警觉的水平差异,低唤醒如睡眠、厌倦、放松等;高唤醒如清醒、紧张等。
由于Valence 和Arousal 两个维度就可以解释绝大部分情绪变化,因此本文仅采用这两个维度作为受试者的情感评价指标,即通过受试者对Valence和Arousal 的评分来判断受试者当前的情绪状态。本文对Valence 和Arousal 进行单独的分类,即LV(Low Valence)表示消极的情绪;HV(High Valence)表示积极的情绪;LA(Low Arousal)表示平静;HA(High Arousal)表示激动;由于Valence 和Arousal 之间具有关联性,因此同时也考虑了结合Valence 和Arousal的分类,即HVHA、HVLA、LVHA、LVLA 4 种情绪状态。在二分类任务中,由于只考虑某一项指标,得分较为均匀,因此可以取中间分数作为阈值为情绪进行划分。本实验的评分在1~9 之间,因此取5 作为阈值。而在四分类任务中,因同时考虑两项指标,导致评价分数点不规则分布。如图2 所示,每个受试者的得分点分布差异过大,若仍然采取阈值的方式进行情绪的划分,会忽略受试者之间的差异性。本文采用K-均值(K-means)聚类方法自适应地将情绪聚成4 类,图2 中的每种颜色分别代表不同的类别,黑色的十字符号表示聚类中心点,可以看出通过聚类的方法能够将4 种情绪比较明显地分隔开。
4 基于小波包分解的特征提取
4.1 小波包分解
特征提取是情感识别的关键环节,本文采用小波包分析方法[17]分解出脑电信号的各个频段,在不同频段上分别对人的情感变化进行识别。小波包分析是小波分析的延伸,其基本思想是让信息能量集中,在细节中寻找有序性,把其中的规律筛选出来,为信号提供一种更加精细的分析方法。在小波包分解的基础上,探讨脑电信号的频段与情感的联系,并选取优势频段,提取相应小波包系数的能量值作为模型的输入特征。
对DEAP 脑电数据采用db4 小波进行4 层分解。原始数据的采样频率为128 Hz,奈奎斯特频率为64 Hz,则进行4 层分解时,共分为 24=16 个频带,每个频带的带宽为64/16=4 Hz。选取每个频带节点利用 式(1)计算得到各个节点的能量值作为识别特征。
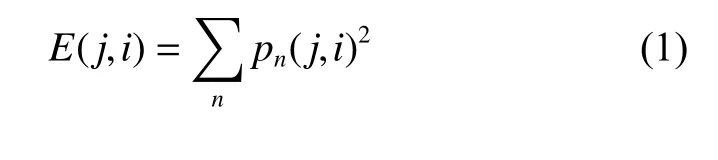
其中:E(j,i)表示在分解层次j上第i个节点的能量值;pn(j,i) 表示第j层第i个节点的n个小波包变换系数。每个样本通过小波包4 层分解可以得到16 维特征,由于本文采取前32 个导联的EEG 信号,因此最终得到的输入序列特征维度为 1 6×32=512 。
4.2 基线(Baseline)处理
本文采用的每个视频片段的基线长度为3 s。由于脑电信号的敏感性较强,因此正常生理活动下的脑电信号很容易对情绪变化时的脑电波造成影响。为了减小这个影响,需要对基线进行消除。通过小波包提取前3 s 数据即基线的特征,然后将后60 s数据的特征分别减去基线特征,以消除基线的影响。
5 基于Snapshot 集成的TCN 情感识别模型的构建
5.1 TCN 模型的架构
TCN 模型与普通CNN 模型的不同点主要在于该结构中的卷积是因果关系,任意一个时刻的状态都考虑了之前的全部状态。
TCN 模型的结构如图3 所示。该模型结构主要为时序卷积层和全连接层,其中M表示一维卷积核的数量,d表示每个卷积核的大小,T表示每秒钟的序列长度,F表示输入序列的特征维度,本文设F=32(导联数) × 16(频带数)=512。输入序列经过一维卷积核的作用得到T×M的时序特征序列,使用修整线性单元(Rectified Linear Unit, ReLU)作为激活函数应用于每一个元素。全连接层用于分类,使用softmax计算当前时刻属于某一类别的概率。

图3 TCN 结构图Fig.3 TCN structure diagram
5.1.1 因果卷积(Casual convolution) 因果卷积首次在WaveNet[18]中提出,是用于处理序列问题而提出来的一种卷积模型。这种卷积模型在某时刻t的预测不能与任何未来时刻的信息相关,如式(2)所示:
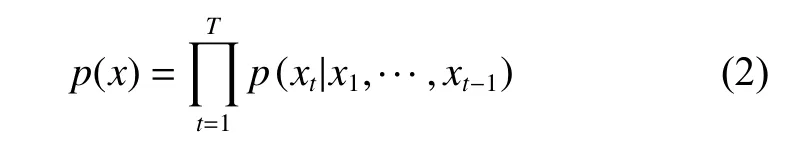
其中:xt表示t时刻的信息。可以看出该时刻的状态只与之前时刻的信息相关。因果卷积模型如图4所示。
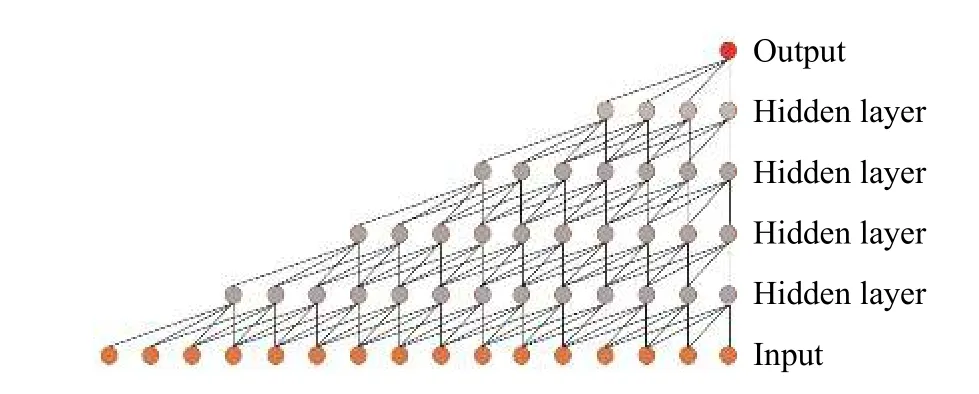
图4 因果卷积模型Fig.4 Casual convolution model
可以看出使用因果卷积的每一个节点都只考虑在此之前的节点,可以很好地用来处理时间序列,但是如果需要考虑比较久远的信息,那么卷积的层数就必须随之增加,这样就会导致深度学习中常见的梯度消失、训练复杂、拟合效果差的问题,因此WaveNet 同时提出了扩张卷积(Dilated convolution)的概念。

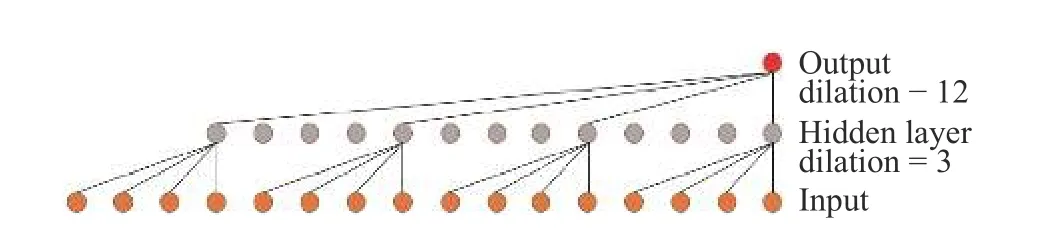
图5 一维扩张卷积Fig.5 One-dimensional expansion convolution model
本文的输入数据是长度为16 的一维脑电序列X=[x1,x2,···,xi] ,设置步长s=1,卷积核fk=4,第k层的扩张率dk=3×4k−1。通过计算可以得到:当不使用扩张卷积时,若要使输出考虑到该序列所有时刻状态,需要4 层的隐藏层单元(如图4 所示),而使用扩张卷积时只需要1 层的隐藏层单元(如图5 所示)。5.1.3 残差模块(Residual block) 残差模块[19]是一种深度神经网络,通过将前一层的信息跳层输入下一层,使得后层的信息更加丰富,能够很好地解决由于增加深度带来的副作用(退化问题)。TCN 模型使用了残差模块。
5.2 Snapshot 快照集成
为了能够更好地训练TCN 模型,本文采用Snapshot 快照集成策略。该方法的原理是通过不断重置学习率来逃避局部极点值。学习率的重置如式(5)所示:

其中: α (t) 表示第t次迭代的学习率; α0表示初始学习率;nb_epochs 表示训练过程总的迭代次数;nb_cycles 表示循环次数,即学习率重置次数。
每次迭代结束时保存当前模型,然后重置学习率为初始学习率进行下一次迭代,如此反复多次,保存多个模型进行集成,如图6 所示。图中横坐标为迭代次数,纵坐标为训练过程的损失值。该训练过程设置的迭代次数为80,循环次数为8,即每10 次迭代重置一次学习率。由图6 可以看出,每次重置学习率都可以使训练过程跳出当前极值,且都能得到不错的收敛,保存训练过程每次循环所产生的模型。

图6 寻优过程图Fig.6 Diagram of optimization process
5.3 投票集成策略
集成学习(Ensemble learning)通过构建并结合多个机器学习模型来完成学习任务,在分类任务中投票法(Voting)是最常用的集成方式。
在本文的模型寻优过程中,每一个局部极小值点的模型都进行了保存。由于这些模型之间存在差异性,因此采用投票集成的方法提高识别精度。如图7 所示,通过Snapshot 方法训练出来的n个TCN模型分别输出各自的识别结果,如类别1、类别2,如果输出类别1 的模型数量多于输出类别2 的模型数量就采用类别1 作为最终识别结果,反之就采用类别2 作为最终结果。

图7 投票集成过程Fig.7 Process of voting ensemble
6 实验结果与分析
TCN 模型在Keras 框架下通过Python 编程实现。实验环境Intel(R) Core(TM) I5-7700HQ CPU @2.80 Hz, 16 GB 内存,NVIDIA GeForce GTX 950 M 显卡,64 位Windows10 系统。
6.1 不同频段的情感识别
将每个受试者的数据分成5 份,每次取其中一份作为测试数据,其余作为训练数据。取5 次交叉实验的识别精度均值作为最终结果,并在训练过程中再次将训练数据随机取出10%作为验证集。
根据验证集确定TCN 模型的部分参数,选择时间窗为1 s,并将每段信号按顺序每62.5 ms 进行一次特征提取,故每秒钟的序列长度为16。此外,根据经验将卷积核数量设为50,卷积核长度设为4,当损失函数连续10 次迭代都没有发生优化时训练终止。
脑电信号一般被分为5 个频段,依次为Delta、Theta、Alpha、Beta 和Gamma,考虑到每个频段可能对情绪状态的敏感度不同,因此本文通过小波包分析提取出各个频段,讨论不同频段对脑电情感的不同影响。
表1 示出了18 个受试者测试精度的平均值。可以看出对于Valence 和Arousal 二分类来说,Beta和Gamma 频段相对于低频段的信号来说对情绪的反应更加敏感,对于A-V 四分类来说Gamma 频段更敏感,而当使用全部频段信息时其识别精度最高。
6.2 不同算法的对比
由于支持向量机(SVM)是较为流行的非深度学习算法,而门控单元循环网络(GRU)是比较具有代表性的深度时序模型,因此本文采用SVM 和GRU 模型与TCN 模型进行二分类和四分类的对比实验。实验结果表明,当惩罚因子C=2,核函数为线性核时,SVM模型验证集分类效果较好。当时间窗设为1 s,隐层单元数为100 时,GRU 模型验证集分类效果较好。

表1 各频段信号的识别精度对比Table 1 Recognition accuracy of signals in each frequency band
Valence 二分类和Arousal 二分类识别结果如图8 和图9 所示,图中蓝色、绿色和黄色折线分别表示TCN、SVM、GRU 模型在18 个受试者上的平均测试精度。可以看到TCN 模型的识别结果相对SVM 模型有明显的提升,而GRU 模型对比SVM 模型也有一定的提升,但效果并不是特别明显,说明序列模型更适合于脑电信号识别研究。对比GRU 模型,TCN 模型不仅在识别精度上有很大的提升,而且在时间复杂度上也具有比较大的优势,其计算效率能够达到GRU 模型的10~15 倍。
A-V 四分类识别结果如图10 所示。可以看到在四分类问题中,SVM 模型的效果并不理想,GRU模型相对于SVM 模型有明显的提高,而TCN模型相对于GRU 和SVM 模型都有比较大的提升。

图8 Valence 二分类结果对比Fig.8 Comparison of valence two classification results

图9 Arousal 二分类结果对比Fig.9 Comparison of arousal two classification results

图10 A-V 四分类结果对比Fig.10 Comparison of A-V four classification results
6.3 Snapshot 寻优及集成策略
综合考虑模型集成的效果和计算复杂度,选择循环次数为8,即通过调整学习率得到8 个训练模型,18 个受试者的测试结果如图11 所示。图中绿色折线表示不加任何集成策略的TCN 模型识别结果,黄色折线表示通过Snapshot 策略寻得的最优模型的识别结果,蓝色折线表示将通过Snapshot 思想得到的各个模型进行集成得到的识别结果。可以看出Snapshot对识别精度有略微的提升,而投票集成方式的识别结果相对于Snapshot 寻得的最优模型也有一定的提高。

图11 Valence 集成策略结果对比Fig.11 Comparison of valence ensemble strategy results
6.4 同类研究对比
6.4.1 二分类研究对比 本文对比了其他采用DEAP数据集的情感识别研究,对比结果如表2 所示。文献[20]通过自编码机制,编码阶段将脑电数据与眼电数据分开建模,解码阶段再组合到一起,形成高阶特征表示,使用SVM 作为分类器,最终对Valence 二分类达到了85.20%的识别精度,对Arousal 二分类达到了80.50%的识别精度;文献[21]将使用残差神经网络(Residual Neural Network,ResNet)提取的特征融合线性频率倒谱系数(Linear Frequency Cestrum Coefficient, LFCC)作为最终特征,使用KNN 作为分类器,最终对Valence 得到90.39%的精度均值,对Arousal 得到89.06%的精度均值;文献[22]考虑了每个受试者对实验音乐MV 的熟悉度,证明了熟悉度对分类结果的影响比较大,采用分形维度(FD)和功率谱密度(PSD)作为特征,采用决策树对Valence 的平均准确率为73.30%,对Arousal 的平均准确率为72.50%;文献[23]使用Relief 算法对32 个通道进行特征选择,利用快速傅里叶变换(FFT)计算功率作为特征,使用概率神经网络(Probabilistic Neural Networks,PNN)作为分类器对Valence 最终得到了81.21%的平均准确率,对Arousal 得到了81.76%的平均准确率;文献[24]采用皮电、眼电等通道数据并为其单独设计特征并且评估了个人因素对实验的影响,提取PSD 特征,使用随机森林算法,最终结果稳定在对Valence 的精度均值为80.10%,对Arousal 的精度均值为77.20%;文献[25]通过小波变换提取特征,使用RNN 作为分类器,最后得到对Valence 的平均识别精度为74.12%,对Arousal的平均识别精度为72.06%。其中文献[20,22,25]使用了非深度学习算法,文献[21,23,24]应用了深度学习算法。
本文以5 作为阈值,在Valence 和Arousal 两个维度上进行二分类,采用TCN 模型取得了最好的平均精度,并通过Snapshot 集成的思想对训练过程进行优化,使得精度进一步提高,实验结果验证了本文方法的可行性。

表2 两种情绪识别精度对比Table 2 Comparison of two emotion recognition accuracy
6.4.2 四分类研究对比 本文在4 种情绪的分类中也能够取得比较明显的效果,结果如表3 所示。文献[26]去除了样本间一致性差的视频,共选取了17 个视频作为实验数据,将数据进行分段,求取每段的alpha 和beta 波段的能量、beta 和theta 波段的能量比率、3 个Hjorth 参数、C0 复杂度、方差和谱熵共计9 个特征,采用KNN 算法对4 类情绪得到了70.04%的识别精度;文献[27]提出了一种针对脑电信号在HRI 领域中使用的实时情绪估计方法获取与内在EEG 模式相关的有意义的特征,使用高斯过程分类器(Gaussian-Process Classifier,GPC)最终得到四分类的识别精度为91.20%;文献[28]选取了所有通道中的15 个通道,采用小波变换的特征,通过SVM 和神经网络对情感进行识别,通过SVM 得到了88.22%的识别精度,通过神经网络得到了90.20%的识别精度。
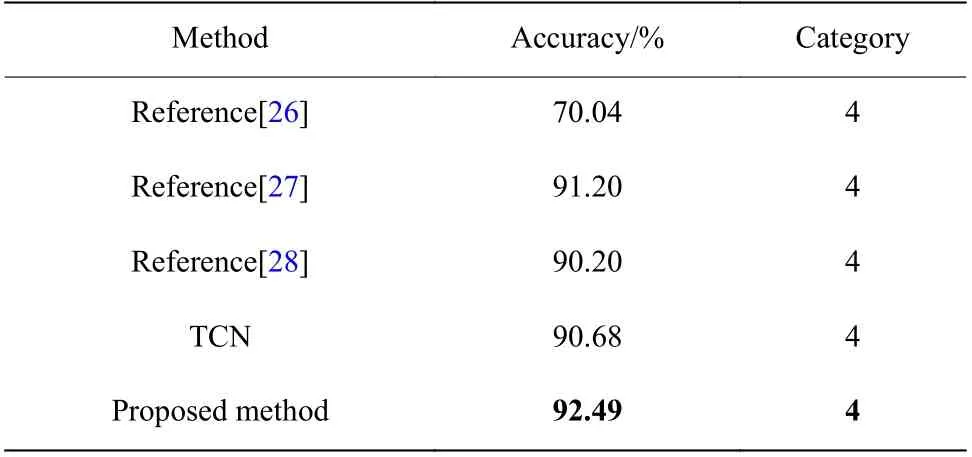
表3 4 种情绪识别精度对比Table 3 Comparison of four emotion recognition accuracy
7 结 论
本文提出了一种基于时序卷积网络的情感识别算法。该算法能够适应脑电信号的时序特征,克服了传统时序网络的计算复杂度过大的缺点,既有RNN 的时序性又有CNN 的并行计算的特点。采用Snapshot 思想和集成思想对模型的训练进行了进一步的提高。对比了不同波段对情感的敏感性,得出脑电信号各频段间和情绪变化的关联,并对比了同类研究结果。实验结果表明本文方法在计算精度和算法复杂度上都有比较好的结果。

