基于逆向思维训练提升数学思维品质的教学研究

◎许遥集 （福建省厦门市新店中学，福建 厦门 361102）

《普通高中数学课程标准（2017 年版）》指出，数学学科核心素养包括“数学抽象”“逻辑推理”“数学建模”“直观想象”“数学运算”“数据分析”六个方面.推理与证明是数学的基本思维过程.在问题解决过程中，推理具有猜测和发现结论、探索和提供思路的作用.数学发散思维的核心是培养学生的创造性思维、创新能力和独立思考能力.逆向思维是发散思维的一种重要形式，它是从已有的习惯思路的反方向去思考和分析问题，表现为逆用定义、定理、公式、法则等.逆向推理，即顺推繁复时考虑逆求；反向证明，即直接解决较困难时考虑间接解决；从反方向形成新结论，即探讨可能性或合理性存在逻辑困难时考虑新的可能性.逆向思维反映了思维过程的间断性、突变性和反联结性，是摆脱思维定式、突破旧有思想框架、产生新思想、发现新知识的重要思维方式.本文基于中学数学教学实践，对重视逆向思维训练、培养学生逆向思维能力及提升学生数学思维的若干方法进行了归纳总结.

一、重视逆向思维的训练

逆向思维是相对正向思维而言的，它的思维方式往往是正向思维的逆转.在数学教材中蕴含着许多可逆性内容，如数学对象的定义、数学运算、原定理与逆定理等.在绝大部分的数学课堂上，教师都要求学生掌握并学会应用一些定义、定理、公式、法则等，但大多都是从左到右的正向运用，久而久之学生就会形成一种思维定式——用固定的思路和习惯去考虑问题和解决问题，这对思维灵活性的培养很不利.为了让学生逐步具备超脱出习惯处理方法界限的能力，训练思维的灵活性，教师在教学中应有意识地在强化正向思维的同时注意逆向思维的训练.

1.注意阐述定义的可逆性

被定义的概念和下定义的概念，其外延完全相等，因而两者的位置可以互换.由此可见，所有的定义都具有可逆性.也就是说，每个定义都可以从正、反两面来加深学生对其的理解.下面我们以例1 为例来说明此问题.

例 1已知关于x的方程 3x＋a＝4 的解是x＝2，求a的值.

（1）正向思维解法

解解方程得解得a＝－2.

（2）逆向思维解法

解∵x＝2 是所给方程的解，代入原方程得3×2＋a＝4，解得a＝－2.

点评对比逆向思维和正向思维两种解法，可以发现逆向思维的解法比正向思维的解法更简捷灵活.

总结在数学教学中，我们应有意识地强调定义的可逆性，这样才能全面、深刻地领会定义，从而灵活地运用定义来解决数学问题.

2.注意公式、法则的逆用

数学教材中存在着大量的公式、法则，如加法与减法、乘法与除法、乘方与开方等互为逆运算，整式的乘法公式与多项式的因式分解公式是互逆公式等.对于学生来说，他们能比较熟练地从左到右运用公式、法则，但不善于从右到左运用公式、法则.因此，在教学中，对于数学公式、法则，教师在讲解其正向应用的同时，要注意探索它的逆向应用.显然，公式、法则的逆用将大大丰富它的内容，扩大它的使用“价值”.

下面以例2 和例3 中两个公式逆用的例子进行说明.

例 2求 cos 20°·cos 40°·cos 80°的值.

点评此题是三角函数求值中的一道常见题目，常规思路是用积化和差公式解决.但我们注意到，各余弦角度间存在着特殊关系，逆用倍角公式 sin 2α＝ 2sinαcosα之后，问题就能迎刃而解.

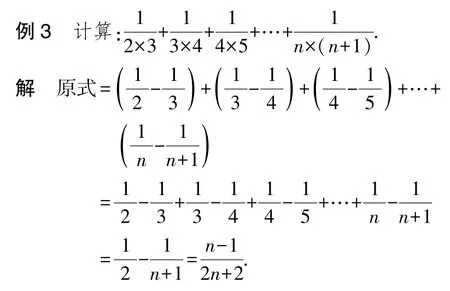
点评对于分式通分法则我们既要会正用，又要会逆用.本题若采用正向思路，则难以解决.学生往往只会把而不会把本题的求解过程逆用了分式通分法则，因而比较顺利地求出了结果.

总结公式、法则的应用应讲究一个“活”字.在很多数学问题的解答中，教师除了引导学生的正向思维，正用公式、法则外，还应启发学生逆用公式、法则，这样可以培养学生思维的变通性与灵活性，培养学生的逆向思维能力.

3.注意数式逆向变形的应用

数式的变形在数学运算过程中发挥着很重要的作用.我们既要会用数式的正向变形，又要会用数式的逆向变形.例4 就是数式逆向变形运用很好的例子.

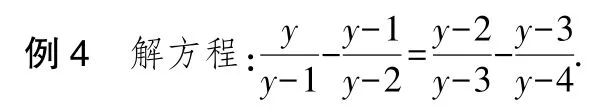
点评本题若采用正向变形，即直接通分，则非常烦琐.这里要注意：数“1”有很多逆向变形.若把“1”灵活地看成等形式，问题便能迎刃而解.

总结在数学问题的解决中，若能灵活应用数“0”“1”等的多种逆向变形，则能立竿见影地解决较为复杂的数学问题.

4.注意阐述原定理与逆定理的可逆性

数学教材中有大量可逆性的原定理与逆定理，如平面几何中等腰三角形的性质定理与等腰三角形的判定定理，平行四边形的性质定理与平行四边形的判定定理等.应强调的是：要注意阐述原定理与逆定理的可逆性，培养学生的逆向思维.

由于教材中有关原定理与逆定理的分析较多，限于篇幅，本文将不再举例说明.

二、执果索因，培养逆向思维能力

执果索因是分析思维中的一种思维方式，它是从结果（或结论）出发追溯其产生的原因的思维方法，其思维过程的主干可表示为：B⇐An⇐An－1⇐An－2⇐…⇐A，其中B是命题的结论（结果），A是命题的条件.分析法侧重于探索性和发现性.在数学教学中，教师既要注意综合法的应用，又要注意分析法的应用，使学生的思维更加深刻并具有创造性.教师可以通过执果索因的思维方法，提高学生的分析能力，很好地培养学生的逆向思维能力.

例5将函数y1＝f（x）图像上所有点的横坐标变为原来的2 倍，再将图像向左平移个单位长度，可得到函数的图像.求y＝f（x）的表达式.

解设函数y1＝f（x）图像上所有点的横坐标变为原来的 2 倍后得到函数y3＝q（x）的图像.

∵ 函数y1＝f（x）图像上所有点的横坐标拉长2 倍，再将图像向左平移个单位长度，得到函数的图像，

点评按常规思路分析：已知y1＝f（x） 变换到直接求函数y＝f（x）学生往往会感到无从1下手.反过来，若能逆向思考，执果索因，则可较快地找出解题途径.函数的图像是由函数y＝f（x）经过1两次变形得到的，所以只要把向右平移个单位长度，得到函数即y＝3再把函数的图像上所有点的横坐标缩短到原来的即可得到函数y＝f（x）的图像，所1以函数

总结采用执果索因的思维方法，在解决某些按常规思路、运用正向思维较难下手的问题时，优越性显而易见.执果索因的思维方法也是我们提高逆向思维能力与分析能力所需要的.

三、创设问题情境，提升数学思维

在解决数学问题时，学生往往会遇到从正面入手较烦琐或较困难的情况，甚至出现一些逻辑上的困境.此时可从辩证思维的观点出发，克服思维定式的消极面，从问题的反面进行思考，创设一定的问题情境，尝试从反面提出假设，通过逆向思维来论证，即采用反证法来论证.这样的训练有利于培养学生的逆向思维能力.

例6求证：关于x的一元二次方程x2＋（2m＋1）x＋m2＝0 和中，不管m取何实数，必有一个或一个以上的方程有实数根.

证明假设若不管m取何实数，一元二次方程x2＋都没有实数根，则可得关于m的不等式组

∴原不等式组无解，在实数范围内不存在这样的m，这与已知矛盾，∴假设不成立.

∴ 不管m取何实数，一元二次方程x2＋（2m＋1）x＋m2＝中必有一个或一个以上的方程有实数根.

点评本题若从正面入手进行证明，则证明过程比较烦琐.若能从结论的反面来考虑，采用反证法，假设不管m取何实数，两个方程都没有实数根，则不难得出所要求证的结论.

总结当从正面入手直接证明较烦琐或较困难时，我们可以反向考虑，有时问题便能迎刃而解.通过创设问题情境，采用反证思想，可很好地培养学生的逆向思维，提高学生思维的发散能力，进一步提高其解题能力.

总之，在中学数学课堂教学中，教师应注重共性、通法的教学，致力于培养学生的思维能力，在重视正向思维的同时要注重逆向思维的培养.逆向思维作为培养学生发散思维能力的一个组成部分，必须引起广大数学教师的重视.