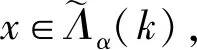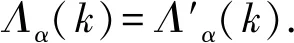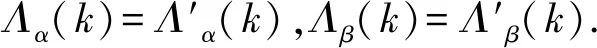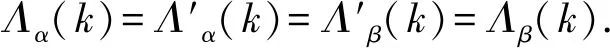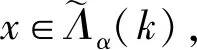半群TOn(k)的格林关系及正则元

甘文秘, 高荣海,罗永贵

(贵州师范大学 数学科学学院, 贵州 贵阳550025)

设S是半群,a,b∈S,若a,b生成相同的主左理想,即S1a=S1b,则称a与b有L关系,记为aLb或(a,b)∈L;若a,b生成相同的主右理想,即aS1=bS1,则称a与b有R关系,记为aRb或(a,b)∈R;若a,b生成相同的主理想,即S1aS1=S1bS1,则称a与b有J关系,记为aJb或(a,b)∈J.令H=L∩R,D=L°R,则L,R,J,H,D是半群S上的等价关系,这5个关系统称为半群S上的格林关系.若a∈S,存在b∈S使得aba=a,则称a是正则元.若a2=a,则称a是幂等元.显然,幂等元是正则元,但正则元不一定是幂等元.

格林关系和正则元的研究是确定1个半群代数结构的基础,对半群的发展有着至关重要的作用,目前已有诸多学者对半群的格林关系及正则性进行了研究.文献[1]论述了格林关系的来龙去脉,得到了诸多广义的格林关系. 文献[2]获得了部分保序且压缩变换半群的格林关系和正则元. 文献[3-5]研究了几类保序变换半群的格林关系和正则元. 文献[6-8]分别获得了半群PO(X,Y,θ)、半群T(X×X)、半群OSn的格林关系和正则元.

为了讨论TOn(k)的格林关系和正则元,给出了下面的准备知识和术语.

设[n]={1,2,…,n}且赋予自然序, 对任意的k∈[n].记[k]={x∈[n]:1≤x≤k},[k]是[n]的非空子集.Tn是[n]上的全变换半群,设α∈Tn,对任意的x,y∈[n].x≤y⟹xα≤yα,则称α是保序的.设On是Tn中所有保序变换之集,则On是Tn的子半群,并称On为[n]上的保序变换半群.令

TOn(k)={α∈Tn:(∀x,y∈[n])x≤y≤k⟹xα≤yα≤k},

则容易验证TOn(k)是Tn的子半群.为了方便,引入以下符号:

对任意的k∈[n].记[k]={x∈[n]:1≤x≤k},对任意的1≤k≤n,任意取α∈TOn(k),令

Λα(k)={x∈lm(α):min(xα-1)≤k},

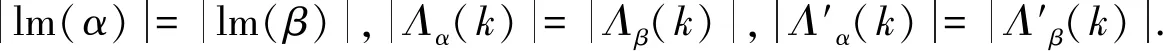
(1)

(2)

注:本文未定义的术语及符号参考文献[9-10].

1 半群TOn(k)的格林关系和正则元

众所周知,在有限半群中,J=D,H=L∩R.因此,本文仅讨论半群TOn(k)上的L,R和D关系.

定理1设α,β∈TOn(k),则(α,β)∈L当且仅当lm(α)=lm(β)且Λα(k)=Λβ(k).

证明设α,β∈TOn(k).假若(α,β)∈L,则存在δ,γ∈(TOn(k)1,使得α=δβ且β=γα.于是lm(α)=(dom(α))α=(dom(α))δβ⊆(dom(β))β=lm(β),同理可证lm(β)⊆lm(α).因此, lm(α)=lm(β).

对任意的x∈Λα(k),则x≤k.于是存在y≤k使得xα-1=y,即yα=x.从而x=yα=(yδ)β,进而y∈dom(δ).由δ∈(TOn(k)1可知yδ≤k,于是x∈Λβ(k).因此Λα(k)⊆Λβ(k).同理可证Λβ(k)⊆Λα(k).因此Λα(k)=Λβ(k).

反之.假若lm(α)=lm(β)且Λα(k)=Λβ(k). 不妨设

其中Λα(k)=Λβ(k)={a1,a2,a3,…,ai},且a1

证明设α,β∈TOn(k).假若(α,β)∈D,则存在γ∈TOn(k)使得(α,γ)∈L且(γ,β)∈R.于是

lm(α)=lm(γ),Λα(k)=Λγ(k),

(3)

于是(amγ-1)β=bm,m∈[1,r].由γ～kβ知,n∈[1,i),m∈[i+1,j],an

显然,α=αβα.为了证明α是正则元,只需要证明β∈TOn(k)即可.

由于α∈TOn(k),则minA1

推论1设α,β∈TOn(k)是正则元,则

1) (α,β)∈L⟺lm(α)=lm(β);

2) (α,β)∈R⟺Ker(α)=Ker(β);

3) (α,β)∈D⟺|lm(α)|=|lm(β)|且|Λα(k)|=|Λβ(k)|.

证明由于推论的必要性是显然的,故只对充分性进行证明.