一种基于自适应相关熵的生命探测方法

吴若凡， 崔国龙， 郭世盛， 李虎泉， 孔令讲

(电子科技大学信息与通信工程学院， 四川成都 611731)

0 引言

在科学技术高度发展的今天，雷达生命迹象探测有着重大的意义。军事方面，在反恐活动中，它可以远距离跨越墙体等障碍物对室内的人体情况进行探测，从而有利于警方判断形势，制定解救人质的方案；救灾方面，当地震、泥石流等自然灾害发生时，受难群众往往被掩埋在倒塌的建筑物或砂石留下的废墟中，通过雷达生命迹象探测技术，救援人员在不进行挖掘的情况下就可以得到被埋人员的大致位置，从而增大搜救成功率；而在医疗方面，医生往往需要对病人呼吸和心率进行监控来判断病人的病情是否有变化，通过雷达的无接触式探测，一方面可以减轻患者的痛苦，另一方面便捷了医院的操作。

在雷达生命迹象探测领域，国内外许多研究机构已经开展了相关研究工作并取得了一定的成果。文献[1]提出了基于短时傅里叶变换的算法，实现了对呼吸频率的有效提取；文献[2]采用变分模态分解(Variational Mode Decomposition, VMD)的算法，成功得到了场景内人体呼吸频率和心跳频率；文献[3]采用希尔伯特振动分解(Hilbert Vibrational Decomposition, HVD)的方法，在穿墙的条件下实现了对多目标呼吸频率的提取。但是上述算法都无法获得场景中目标的距离信息。文献[4]基于步进频连续波雷达，提出了一种利用距离门和动目标检测(Moving Target Detection, MTD)滤波的生命迹象探测方法，实现了目标测距和频率信息的获取。文献[5]基于调频连续波雷达，提出了一种双参数最小均方(Least Mean Square, LMS)滤波器的生命信号提取算法，有效地分离出了多目标的呼吸和心跳信号。文献[6]提出了一种基于互相关熵的生命迹象探测方法，实现了在非高斯噪声背景下的生命迹象探测与参数估计。然而，当场景中的人体目标被其他目标遮挡时，采用上述方法难以实现对所有目标的探测。

为了解决遮挡目标的探测问题，文献[7-8]采用了基于多站雷达的互相关算法，该类算法虽然可以实现对遮挡场景中所有目标的探测，但是却需要用到多台雷达，并且对雷达的放置位置有着较为严格的要求，故实际使用时具有一定的局限性。为了克服这一局限性，本文在一发一收步进频连续波雷达体制下，提出了一种基于自适应相关熵的生命迹象探测方法，利用预检测得到目标可能出现的距离单元及对应的幅度，从而自适应地调节不同距离单元上相关熵的参数，通过对每个距离单元上不同周期的数据进行相关熵处理，实现了对弱目标的增强，最终在RD平面得到了包括遮挡目标在内所有人体目标的呼吸频率和距离信息。

1 回波模型

假设发射波形s(t)为步进频信号，可以表示为[4]

(1)

式中，N为步进频率数，f0为起始频率，Δf为步进频率间隔，T为步进持续时长。

假设探测的目标个数为P，第p个目标的初始距离r0p,所有目标除了呼吸和心跳微动以外没有其他运动，则第p个目标到雷达的实时距离，可以写成

rp(t)=r0p+Δrp(t)

(2)

式中，Δrp(t)为第p个目标心跳和呼吸所引起的微动位移，一般将其建模成正弦信号的形式，具体表示如下：

Δrp(t)=AH,psin(2πfH,pt+φH,p)+

AB,psin(2πfB,pt+φB,p)

(3)

式中：AH,p，fH,p，φH,p表示第p个目标心跳的幅度、频率和初相位；AB,p，fB,p，φB,p表示第p个目标呼吸的幅度、频率和初相位。由于心跳的回波信号在实际应用中十分微弱，因此本文中只考虑了呼吸对雷达回波的影响。对应的雷达回波时延表达式为

(4)

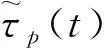
(5)

Sc(m,t)=

(6)

式中，m=1,2,…,M，M为处理的总周期数，Γp为第p个目标的反射系数。对接收到的回波信号进行I/Q解调，得到正交两路差拍信号。再将两路差拍信号变成数字信号并进行周期为T的重采样，就可以得到包含人体微动信息的基带复数信号：

(7)

式中，n=0,1,2,…,N-1。

观察式(7)可知，基带信号c(m,n)等效于是对频域信号进行周期为Δf的采样得到的，所以又可以表示为

(8)

式中，f=0,Δf,2Δf,…,(N-1)Δf，用于频域表达式。通过对式(8)进行补零，可得到

(9)

式中，f′=f0,f0+Δf,…,f0+(N-1)Δf，B为发射信号带宽,B=(N-1)Δf，fc=f0+B/2为中心频率。

对式(9)进行逆傅里叶变换(IFFT)，可以得到

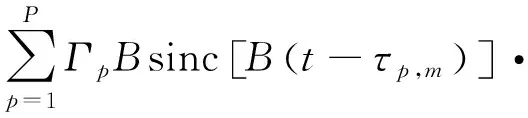
exp(-j2πfc(t-τp,m))

(10)

当回波时延t=τp,m，第p个sinc脉冲幅度达到最大值，又因为τ和目标距离有着一一对应的关系，因此式(10)的结果就包含了所有目标的距离信息。对式(10)的结果沿快时间域进行采样，即可得到回波的多帧距离像，其表达式为

exp(-j2πfc(tk-τp,m))

(11)

式中,k=1,2,…,K为距离单元序数，K为距离单元的总数。由式(11)可知，|Γp|直接关系到第p个目标在距离像上的幅度。Γp的主要影响因素为目标的雷达散射截面积(Radar-Cross Section, RCS)和目标到雷达的距离[9]。对于生命探测，在探测场地不大的时候，上述两个因素对Γp的影响有限，不同目标的回波强度相差并不大。但是，一旦场景中存在两个或以上的目标出现在雷达同一个方位向上，前方目标就会对后方目标构成遮挡。不妨假设有两个目标出现在雷达同一个方位向上，第s个目标被前方目标遮挡了，那么此时式(11)可以写成

d(m,k)=ΓsBsinc[B(tk-τs,m)]·

exp(-j2πfc(tk-τs,m))+

exp(-j2πfc(tk-τp,m))

(12)

对于被遮挡的第s个目标，雷达信号在到达和返回时都会因穿透遮挡它的前方目标而产生衰减，故Γs和Γp≠s往往会有较大的差距。由式(12)可以看出，直接由峰值对目标进行检测会造成遮挡目标的探测困难。

2 基于自适应相关熵的生命探测算法

针对传统算法难以解决的遮挡目标探测问题，本文提出了一种基于自适应相关熵的检测算法对这些微弱目标进行自适应的增强，使它们更加容易被检测出。

2.1 相关熵的定义与分析

随机过程相关熵的定义式为[6]

(13)

式中，E[·]表示随机过程变量xt的数学期望，而

(14)

将式(14)代入式(13)，经由指数函数的泰勒级数展开，可以得到

(15)

对于离散时间平稳随机过程，自相关熵可表示为

V[m]=E[k(x(n)-x*(n-m))]

(16)

式中，x(n)为离散时间随机过程。自相关熵V[m]可以通过式(17)计算得到：

(17)

V[m]的傅里叶变换表达式为

(18)

P(ω)即为相关熵谱，它体现了随机过程的频域特征。在雷达生命探测中，P(ω)就包含了目标的呼吸频率信息[10]。

为了进一步明确σ参数会对相关熵处理的输出结果以及最终生命探测的效果所带来的影响，以下将会进行简要分析。

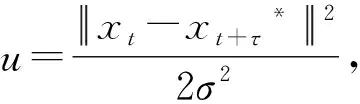
图1 函数k(u)随u的变化曲线示意图

考虑到二范数平方非负的特性，自变量u取值范围为u>0。观察图1的变化曲线，可以直观地得出：当自变量u位于虚线右侧时，相关熵的输出随自变量的变化十分微弱，几乎无法体现出原始数据的变化特征；只有当自变量u位于虚线左侧时，相关熵的输出才可以较好地反映原始数据的变化规律。为了方便起见，我们将虚线左侧的自变量区间称为“最适区间”，对应的相关熵输出称为“最适输出”。

而对于生命探测，目标区别于噪声和杂波的最重要的特征就是目标所在距离单元的值会随着时间(不同帧之间)呈现出周期性的变化规律。因此，对于目标所在距离单元，我们希望相关熵的自变量u应位于最适区间内。与之对应的，噪声和杂波处，我们则希望其自变量u位于最适区间外。

在实际算法应用中，相关熵处理会依次遍历所有的距离单元，对应的上述自变量u的分子||xt-xt+τ*||2中，xt即为该距离单元内第t个周期的数据。一般情况下，在周期间隔τ相同时，不同距离单元上的回波强度将会直接影响到该分子的值，回波强度越大则分子的值也越大。

因此，为了让不同强度的目标的自变量均位于最适区间内，分母σ的值也需要随着回波强度的变化而变化。

2.2 自适应相关熵算法

为了让不同强度的目标的自变量均位于最适区间内，本文提出了基于自适应相关熵的算法。整个算法的流程图如图2所示。

图2 算法的流程图

由于IFFT得到的距离像-周期平面中含有大量静态物体的杂波以及部分直流耦合，故首先需要进行动目标显示(Moving Target Indicator, MTI)处理，沿慢时间域进行均值对消：

(19)

经过MTI处理后的距离像-周期矩阵通过自适应相关熵处理，得到增强了弱目标的RD平面。随后在该平面进行人数判决与目标测距，最终输出目标的人数、呼吸频率和对应的到雷达的距离。以下依次详细介绍整个算法的流程。

2.2.1 自适应相关熵处理

为了合理选取不同距离单元上σ参数的值，算法采用了目标预检测，首先对多周期的数据进行非相干积累

(20)

式中，D为积累后的幅度，K为距离单元数。然后对D(k)使用低门限检测的方法进行目标预检测，得到目标可能出现的距离单元序数和对应的积累幅值

(21)

式中，Lacc为目标可能出现的距离单元序数，A为对应的积累幅值，ε为一个较低的门限。接着根据这些距离单元的积累幅值按照一定比例自适应地调节对应距离单元σ参数的值：

σtarget=βA

(22)

式中，σtarget为使目标处取得最适输出的参数，β为比例系数。以此为基础对每个距离单元的数据进行相关熵处理，对应的公式为

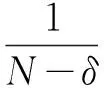
(23)

式中，V(δ,k)表示对第k个距离单元周期间隔为δ的两个数据进行相关熵处理的结果，δ=1,2,…,M-1。σ(k)为第k个距离单元上的σ参数，其表达式为

除此之外，高速公路工程中的中心试验室也可以结合管理部门制定的各项管理制度，对工程各项数据进行综合分析，针对施工材料使用过程中遇到的问题，提出妥善的建议，保证工程中的施工材料得到充分利用。对于高速公路工程中的施工单位来讲，要根据中心试验室提出的意见，对原有的施工工艺进行有效改进，在保证高速公路工程整体施工质量的基础上，真正达到提高工程施工质量控制水平的目的。

(24)

式中，S为一个远小于σtarget的数值，ε为过渡单元数，代表着目标所影响的其两侧距离单元的总数。

V(δ,k)中，所有预检测中得到的目标都已经得到了自适应增强。随后对V(δ,k)进行低通滤波，去除那些预检测中的由噪声和杂波所带来的虚警。

最后，对V(δ,k)沿慢时间域进行快速傅里叶变换(Fast Fourier Transform, FFT)得到RD平面，从相关熵谱中提取出目标的呼吸频率。

2.2.2 人数判决与目标测距

为了在RD平面进行目标检测，首先对该平面中的点进行二值化处理，然后进行基于密度的带有噪声的空间聚类(Density Based Spatial Clustering of Applications with Noise, DBSCAN)[11]。该聚类方法可以自适应地提取出各个目标处的形心坐标而不必事先设定目标的个数。聚类得到的类别数即为目标人数，得到的频率fDBSCAN即为目标的呼吸频率。

为了减少由聚类引入的目标距离与真实值的误差。本文将聚类得出的目标距离和目标预检测的结果进行对比与匹配，以得出与真实值偏差最小的目标距离。令聚类得出的目标所在的距离单元序数为LDBSCAN，最终输出的目标距离单元数为L，则匹配的过程可以由下式表示：

L=Lacc(argmin(|Lacc-LDBSCAN|))

(25)

3 仿真结果

表1 雷达和场景参数

表2 人体目标参数

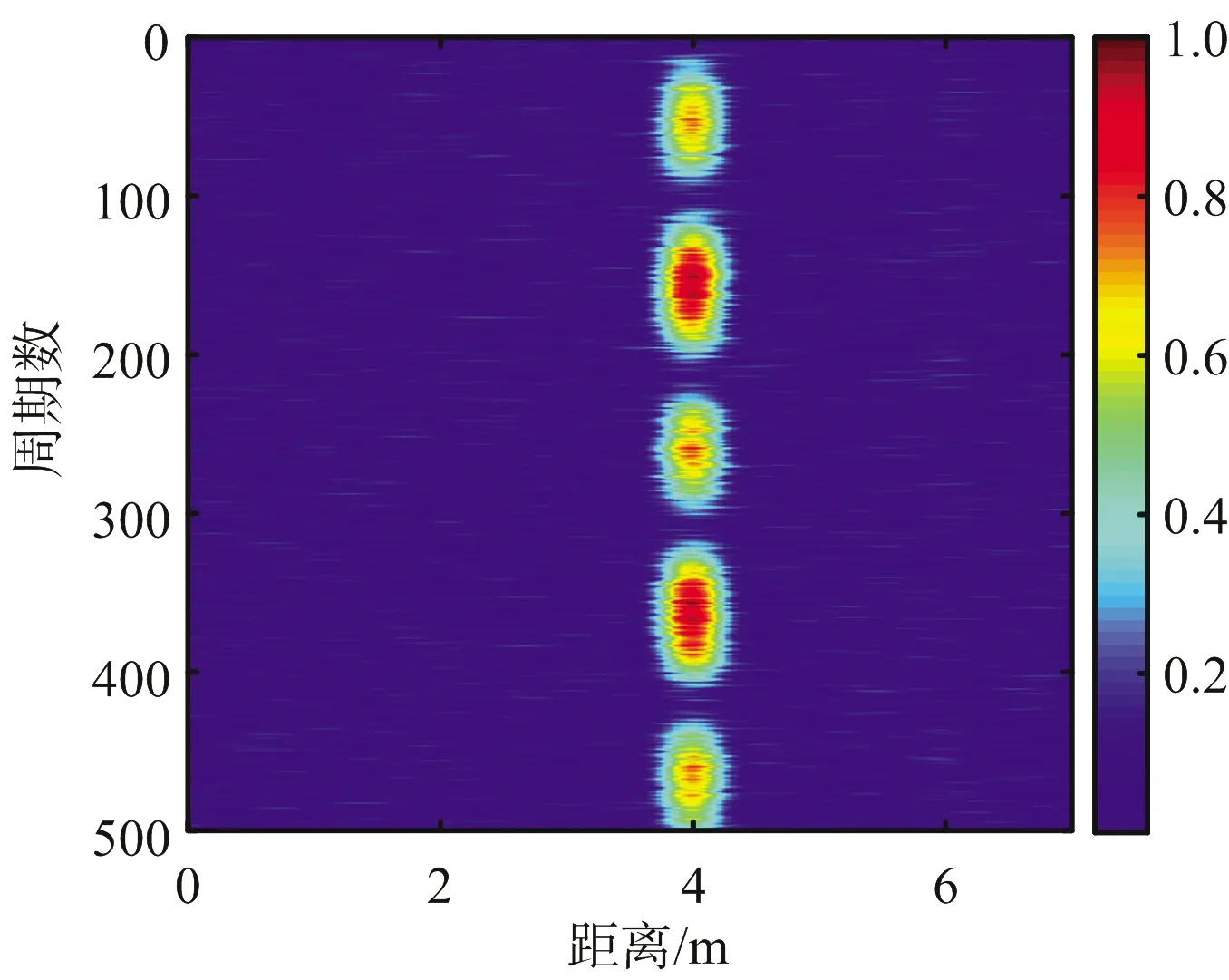
(a) 距离像平面

(b) 非相干积累处理结果

(c) 经相关熵处理后的RD平面

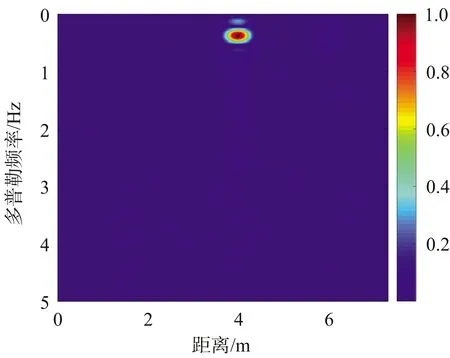
(d) 直接FFT得到的RD平面图3 各阶段仿真结果

图3(a)是MTI后得到的距离像-周期平面的结果，可以看出6 m处的目标由于被遮挡，其幅度比4 m处的目标弱很多。按照文中提出的方法，非相干积累的处理结果在图3(b)中显示，通过一个较低的门限进行检测后，得到的目标可能出现的位置为4.010 0，6.005 9，7.122 8，0.897 2和2.124 0 m，对应的积累幅值分别为4.044 7，0.658 8，0.542 7，0.534 3和0.524 6。以此为基础进行自适应相关熵处理，得到RD平面的结果如图3(c)所示，可以看出4 m和6 m的目标在RD平面上都很强，并且具有明显的呼吸频率特征。最终经由人数判决和目标测距，得到目标人数为2个，距离为4.010 0和6.005 9 m，呼吸频率为0.414 8 Hz和0.506 5 Hz。与仿真中设定的距离和频率几乎完全一致。为了方便进行对比，图3(d)给出了采用传统的傅里叶变换算法，即在距离像-周期平面直接沿慢时间域进行加窗FFT处理，得到的RD平面结果。可以发现在该RD平面中，后方6 m的目标十分微弱，难以进行检测。

通过对比图3(c)、(d)可以证明，该算法拥有弱目标增强的效果，可以有效得出遮挡目标的距离和呼吸频率信息，由此证明了该算法的有效性。

4 实测数据处理结果

为了进一步验证算法在实际应用中对遮挡目标探测的有效性，我们进行了相关实验，并对采集到的数据进行了处理。实验采用一发一收步进频连续波雷达，雷达系统的参数见表2。其中，由于实验条件限制，实际处理的周期数为350而不是仿真中的500。墙体厚度大约为30 cm。

穿墙实验场景如图4(a)所示，图中右上角为雷达的照片。

(a) 场景照片

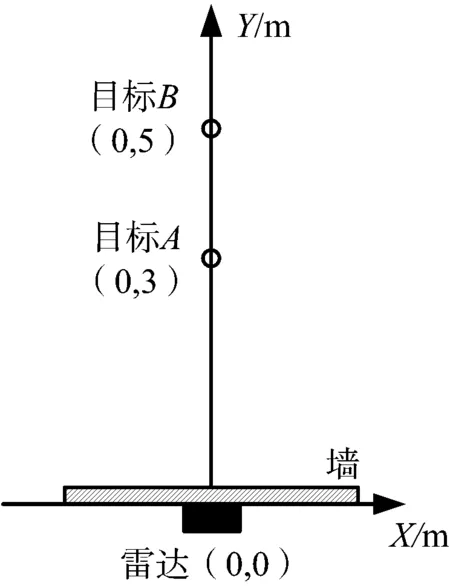
(b) 坐标系示意图图4 双目标遮挡场景

为了便于描述目标和雷达的位置关系，建立如图4(b)所示的坐标系：雷达位于坐标原点(0,0) m，紧贴着墙体拜访，朝向Y轴正方向，两个目标一前一后站立，对应的坐标分别为(0,3) m和(0,5) m。在该场景中，前方目标对后方目标构成了遮挡。

经过MTI处理后得到距离像-周期平面的结果如图5(a)所示。可以看出,3 m的目标十分明显，但是5 m的目标由于被遮挡而显得十分微弱。图5(b)是非相干积累的处理结果，通过低门限的检测后，得到疑似目标的位置为3 m和5 m两处，对应的积累幅度为147.9和12.31。以此为基础进行自适应相关熵处理，得到的结果见图5(c)，与图5(a)对比可以发现，5 m处的遮挡目标得到了明显的增强，和3 m处的目标有着相近的幅度。最后在经由人数判决和目标测距后，得到的目标人数为2人，呼吸频率分别为0.28 Hz和0.31 Hz，为人正常的呼吸频率； 距离分别为3.021 2 m和4.943 8 m，与目标实际距离的误差仅为0.70%和1.14%。为了方便进行对比，图5(d)给出了传统的傅里叶变换算法得到的RD平面结果，很明显后方5 m的目标十分微弱，难以进行检测。在经由人数判决和目标测距后，得到的目标人数仅为1人，距离为3.021 2 m。由此可见,传统算法在该场景中无法探测到后方被遮挡的目标。

(a) 距离像-周期平面

(b) 非相干积累处理结果

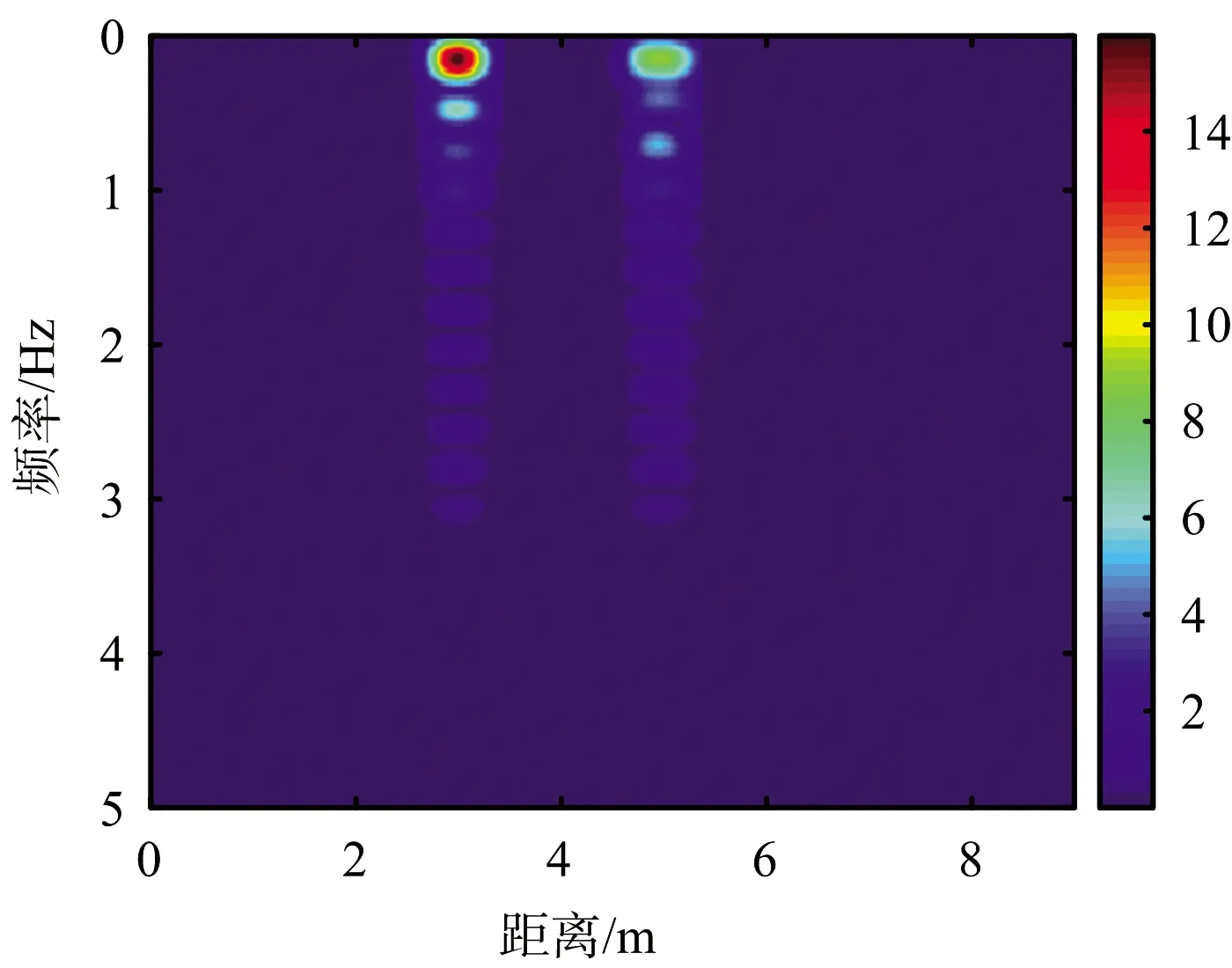
(c) 经相关熵处理后的RD平面

(d) 直接FFT得到的RD平面图5 实测数据处理结果

5 结束语

本文提出了一种基于自适应相关熵的生命迹象探测算法，利用预检测得到目标可能出现的距离单元及对应的幅度，从而自适应地调节相关熵在不同距离单元的σ参数，通过对每个距离单元上不同周期的数据进行相关熵处理，实现了对弱目标的增强。之后采用低通滤波的方式，去除由预检测引入的噪声和杂波干扰，最终在RD平面得到了所有人体目标的呼吸频率和距离信息。实验证明，在存在遮挡现象的多目标场景中，传统的傅里叶变换算法无法探测到后方被遮挡的目标；而使用文中提出的算法可以有效实现对弱目标的增强，从而测得包括遮挡目标在内所有人体目标的呼吸频率和距离信息，测距误差在2%以内。