基于极限学习机的目标智能威胁感知技术

王永坤，郑世友，邓晓波

(1. 中国航空工业集团公司雷华电子技术研究所， 江苏无锡 214063；2. 航空电子系统射频综合仿真航空科技重点实验室， 江苏无锡 214063)

0 引言

当前空战决策仍依赖飞行员对各类传感器获取的多维态势信息进行融合分析，并通过人为经验进行目标威胁估计，进而完成作战决策。这种传统作战方式下的感知与决策，一方面带有人为主观判断，易引发战场不确定性；另一方面，不利于加速OODA环的迭代，无法做到先敌发现、先敌攻击。此外，下一代空战环境的典型特点是无人化、智能化、体系化[1]。大型无人作战飞机将是未来空战的主角，智能化的目标威胁感知[2-3]作为大型无人作战飞机自主空战的关键支撑技术，是实现智能化空战[4-5]的基础。

针对未来智能化空战的典型关键技术需求，目标威胁估计技术获得了国内外学者的广泛研究。目前国内外研究较多的目标威胁估计方法有多属性决策法[6-7]、模糊逻辑法[8-11]、贝叶斯网络法[12-14]以及神经网络方法[15-17]等。多属性决策法[6]首先需要设定影响威胁评估的各态势因素固定权重值，不同的权重值设置对威胁评估结果有很大影响，算法鲁棒性较差。模糊逻辑法[9]算法复杂性较高，不适于工程应用。基于贝叶斯网络算法[12]的威胁估计重点在于推理估计各态势因子对目标威胁度的影响概率，当态势因子维度较高时，各影响因子的概率推理复杂度将会呈指数级上升。神经网络方法[15-16]本质上属于数据化方法，通常借助专家知识数据进行训练建模，实现对目标威胁度的自主感知。但是，传统的BP[17-18]神经网络算法泛化能力有限，而且随着样本数增加，算法实时性将会大幅下降，无法做到在线学习。

极限学习机(Extreme Learning Machine, ELM)是由Huang等[19-20]提出的一种新型神经网络算法，输入权值和偏置量是随机初始生成，输出权值随输入权值和偏差的变化得到。该算法相比经典的BP神经网络算法，首先具有学习速度快的优势，此外，BP算法存在过度训练的问题，使其泛化能力变差，而ELM具有较好的模型泛化能力，而且算法的高实时性使其广泛应用于在线学习系统[21-22]。本文基于ELM算法进行空中目标威胁智能感知问题研究，首先对影响目标威胁度的态势因子进行分析提取，并采用隶属度函数[23]对各态势因子进行归一化数值解译；然后，采用极限学习机对威胁估计的输入输出样本数据进行训练建模，最后采用多组测试样本进行了与BP算法的对比仿真验证。

1 威胁感知态势因子提取

本文针对战斗机空空作战中的目标威胁感知问题进行研究，首先需要进行空中目标态势因子的提取。在空战中，目标的威胁属性是基于飞机上各传感器获取的信息进行综合判定，一般包括目标距离、速度、角度、机动性、目标类型、攻击能力、情报信息等十多种态势因子。但是在实际作战中，由于计算资源和实时性的限制，无法融合所有维度的态势信息进行威胁判定，因此，选择权重属性较高的态势因子进行目标威胁综合感知。

本文借助专家知识，从定性和定量两个方面选择高权重的态势信息。针对定量因子，目标的距离和速度是从机载雷达可获取的最直观信息，也是进行威胁判定的基础；此外，目标相对我方平台的进入角也是需要考虑的一个重要因素，不同的进入角决定着敌方对我方实施攻击的概率；再者，对目标探测的跟踪精度是对敌方目标作战意图预测的重要基础，而且较差的目标航迹质量大概意味着目标在作高机动运动，因此，目标的机动性也会影响对其探测的航迹质量。定性因子主要是目标类型，不同类型的目标具备不同的攻击能力，是决定目标威胁的一个关键属性。因此，空中目标威胁感知的态势因子类型如图1所示，集合为Tr={Tr1,Tr2,Tr3,Tr4,Tr5}={目标距离，目标速度，进入角，航迹精度，目标类型}。

图1 空中目标威胁态势因子类型

2 基于模糊隶属函数的态势因子解译

1) 目标距离隶属度函数

目标距离信息由机载雷达获取，距离越近，对我方平台威胁度越大，因此，其隶属度函数值应随距离增加而单调下降。具体函数选取为

(1)

式中，a1=0.3R，a2=R，a3=1.15R，R是雷达探测距离,x1表示目标距离。

2) 目标速度隶属度函数

战斗机空战过程中主要面临亚音速飞机、超音速战机以及超音速空空导弹等目标威胁，而高超声速目标的攻击对象一般不会是作战飞机，因此，目标速度隶属度函数符合中间型分布函数形式，在低速和超高速区函数值较小。具体函数选取为

(2)

式中，a=2 Ma，a1=0.5 Ma，a2=1.2 Ma，a3=2.5 Ma，x2表示目标速度。

3) 目标进入角隶属度函数

目标进入角以我平台与目标连线为基准，顺时针方向为正。当目标进入角在-90°～90°区间时，函数值为正，且当目标进入角越接近0°，函数值越大。具体函数选取为

(3)

式中，k=3.5，x3表示目标进入角。

4) 目标航迹精度隶属度函数

目标航迹精度隶属度函数符合单调函数形式，对目标的跟踪精度越高，越有利于对目标意图的准确估计。因此，其函数值应随跟踪精度下降而单调上升。具体函数选取为

(4)

式中，k=2.75×10-5，a1=30，a2=300，x4表示目标跟踪航迹质量。

5) 目标类型的隶属度函数

战斗机空战中面对的目标类型包括各类作战飞机以及敌机发射的空空导弹等，根据各类目标的攻击能力不同，给定隶属度函数如下：

(5)

3 基于极限学习机的目标威胁智能感知

本节基于极限学习机(ELM)算法进行目标威胁智能感知技术研究，通过对威胁感知的输入输出样本数据进行学习建模，自主得到威胁感知结果，而不必进行繁琐的权重调节步骤。

3.1 ELM算法原理

极限学习机是机器学习领域中的一种新型高效算法，以单隐层前馈神经网络架构为基础，通过高斯均匀随机分布生成的固定权值矩阵实现输入层到隐含层的连接，而隐含层与输出层的加权矩阵的学习是ELM算法建模的主要目标。因此，ELM算法只需设置训练网络的隐层节点个数，不需要调整网络的输入权值以及隐层神经元的偏置。基于上述描述可知，ELM算法具备参数选择容易、学习速度快的优势。特别是在可用空战数据样本有限的条件下，能够以零误差逼近任意的线性和非线性函数。

极限学习机的具体算法原理如下：给定N个样本(ui,ti)，其中ui=[ui1,ui2,…,uiNu]T和ti=[ti1,ti2,…,tiNy]T分别为样本输入输出数据，Nx个隐层神经节点，Nx≤N，激活函数为h(u)的单隐层前馈神经网络数学模型为

j=1,…,N

(6)

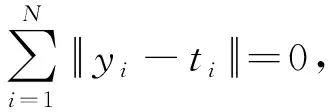
(7)

上述方程的矩阵形式为

Ηβ=T

(8)

式中，

(9)

H为极限学习机的隐含层输出矩阵，其中第i列代表第i个隐层神经元关于每个输入向量u1,u2,…,uN的输出。

(10)

等同于求最小化全局误差E：

(11)

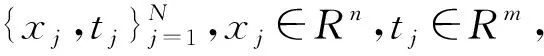
一般情况下，隐层节点数远远小于训练样本数，即Nx≪N，因此需要求H的伪逆，即

(12)

式中，H†为隐含层输出矩阵H的广义摩尔逆[24]。当HTH非奇异时，H†=(HTH)-1HT，当HHT非奇异时，H†=HT(HHT)-1。根据岭回归原理[25]，求得的H†为

H†=(HTH+λI)-1HT

(13)

3.2 基于ELM的目标威胁智能感知

本文采用极限学习机技术实现空中目标智能威胁感知，首先选取输入输出数据，其中输入数据为五维，包括目标距离、目标速度、目标进入角、目标类型以及目标航迹精度，输出为目标的威胁度，并将样本数据以一定比例划分为训练样本和测试样本，模型示意图如图2所示；然后，采用ELM算法对训练样本的输入输出数据进行训练建模；训练完成后，采用测试样本进行结果测试，如果精度不满足，重新训练。

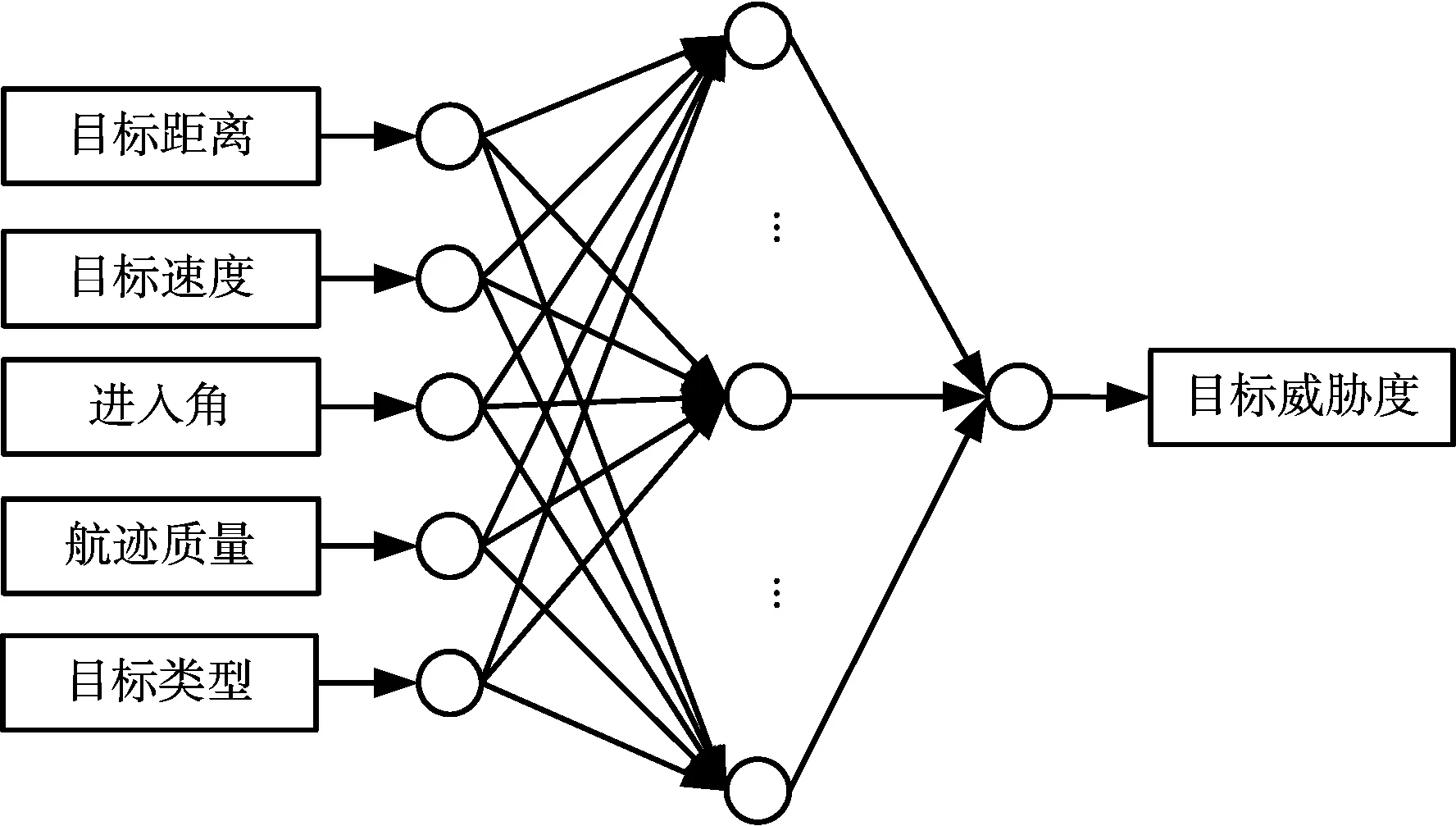
图2 空中目标威胁ELM模型

具体步骤如下：

步骤1： 选取样本数据，包括五维输入样本，目标距离特征、目标类型、速度、目标进入角以及航迹精度，输出样本数据即目标威胁度；

步骤2： 将样本数据按一定比例划分为训练样本和测试样本数据；

步骤3： 选择ELM算法进行建模训练，由于本文研究问题属于回归问题，因此针对回归问题设置ELM算法参数，即类型参数与隐层节点参数；

步骤4： 采用训练样本数据进行建模训练；

步骤5： 采用测试样本数据进行模型测试，精度满足要求，则进入下一步，否则返回步骤3调整参数重新训练；

步骤6： 结束。

4 算例分析与验证

4.1 样本数据选取

本节采用ELM算法对目标威胁估计进行特征建模，从而实现目标威胁智能感知。从某目标威胁数据库选取目标威胁样本数据，其中输入样本包括五维，即目标距离特征、目标类型、速度、攻击角以及航迹质量，样本选取策略如表1所示。

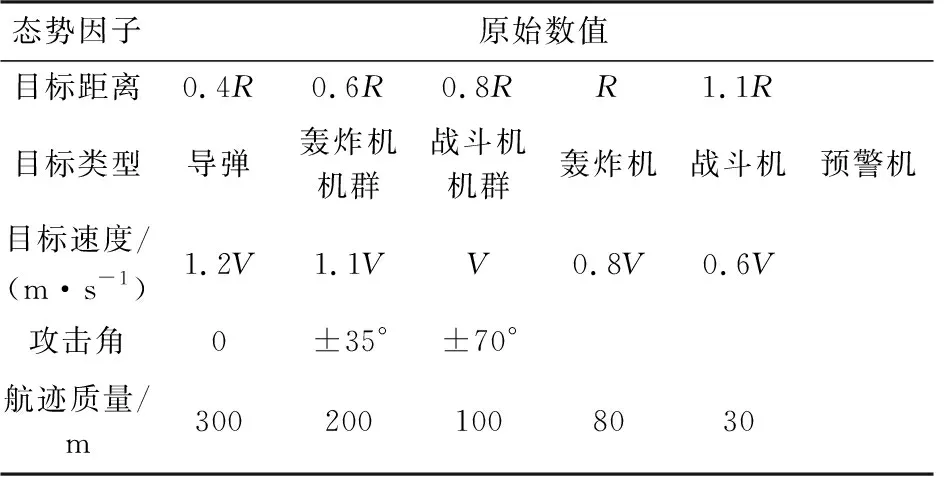
表1 目标威胁度输入样本

其中距离因子中的R=200 km，速度特征中的V表示声速。各特征值的归一化隶属度函数计算结果如表2所示。

表2 输入样本的隶属度函数值

通过上述数据预处理，选取的样本数据共 2 250组。按均匀分布随机抽取2 000组数据作为训练样本，250组数据作为测试样本。

为了更好地说明采用ELM算法进行目标威胁感知的合理性，采用ELM和BP算法对比验证。ELM采用随机的方式设置输入权值及隐层神经元的偏置，只需设置隐层神经元个数，设置为100；BP算法学习率设置为0.1，训练目标1.0×10-5，隐层神经元个数同ELM算法。

4.2 仿真结果

首先选定2 000组样本进行训练，250组样本进行测试。测试结果如图3和图4所示。从图4统计的预测误差百分比可知，ELM预测误差基本在0.1%的水平，BP的误差百分比约为0.5%，ELM大大低于BP算法的预测误差百分比。此外，统计得到250组样本中，ELM的预测均值误差为5.0×10-4，BP的预测均值误差为1.4×10-3。因此，基于ELM算法训练得到的感知模型具有较高的威胁估计精度。

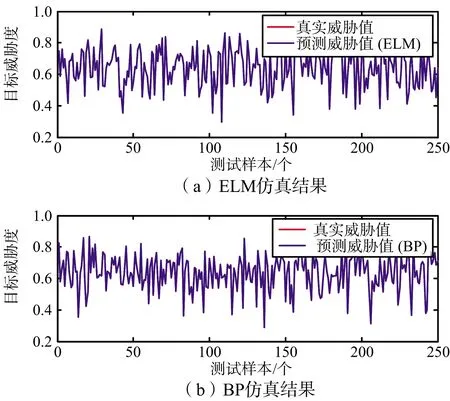
图3 测试样本目标威胁估计结果(250组)

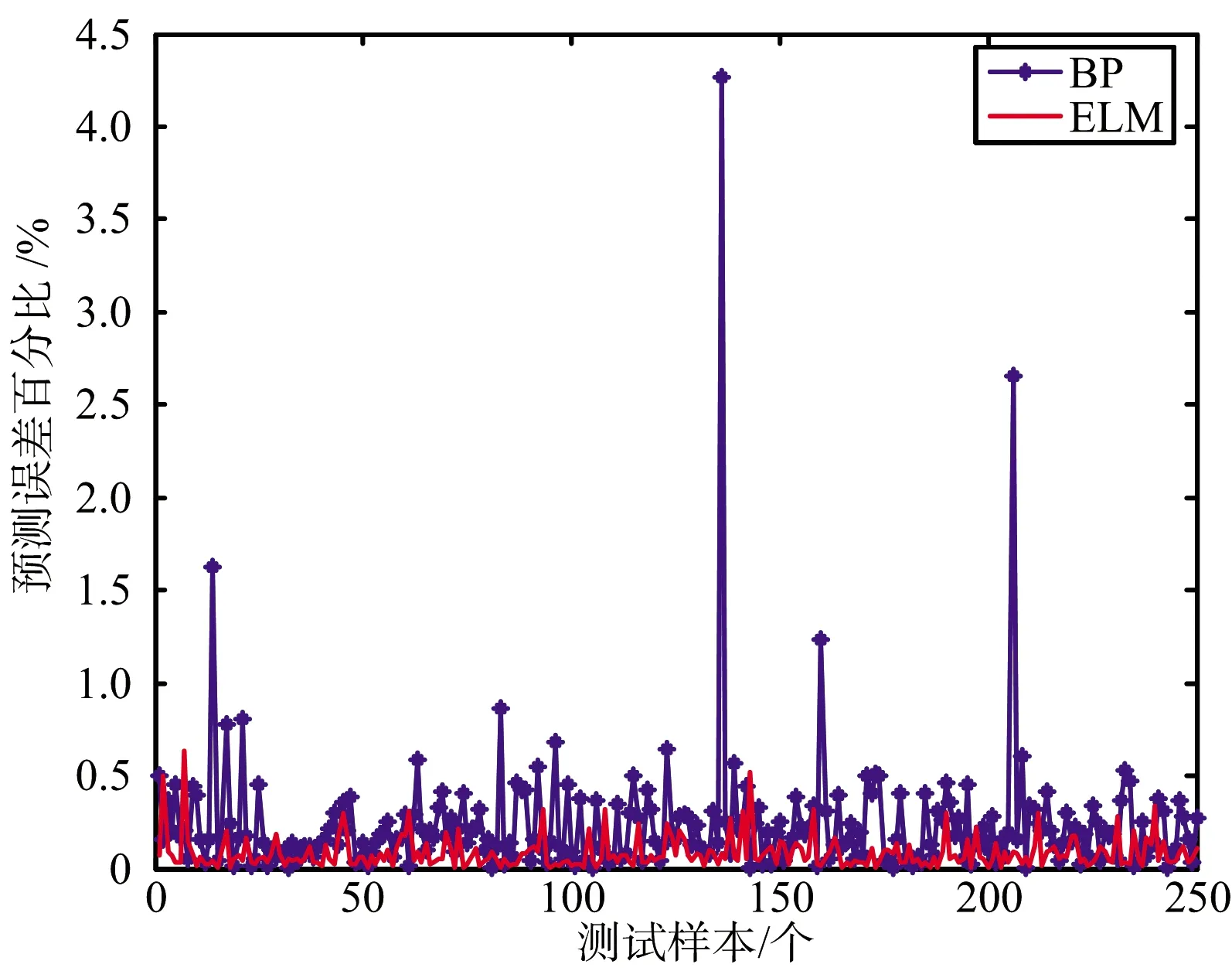
图4 目标威胁估计误差百分比 (250组)

选定1 750组样本数据进行模型训练，500组数据作为测试，测试结果如图5和图6所示。ELM和BP的威胁估计均值误差分别为5.2×10-4和1.6×10-3，ELM的估计精度较BP算法有一个量级的提升。

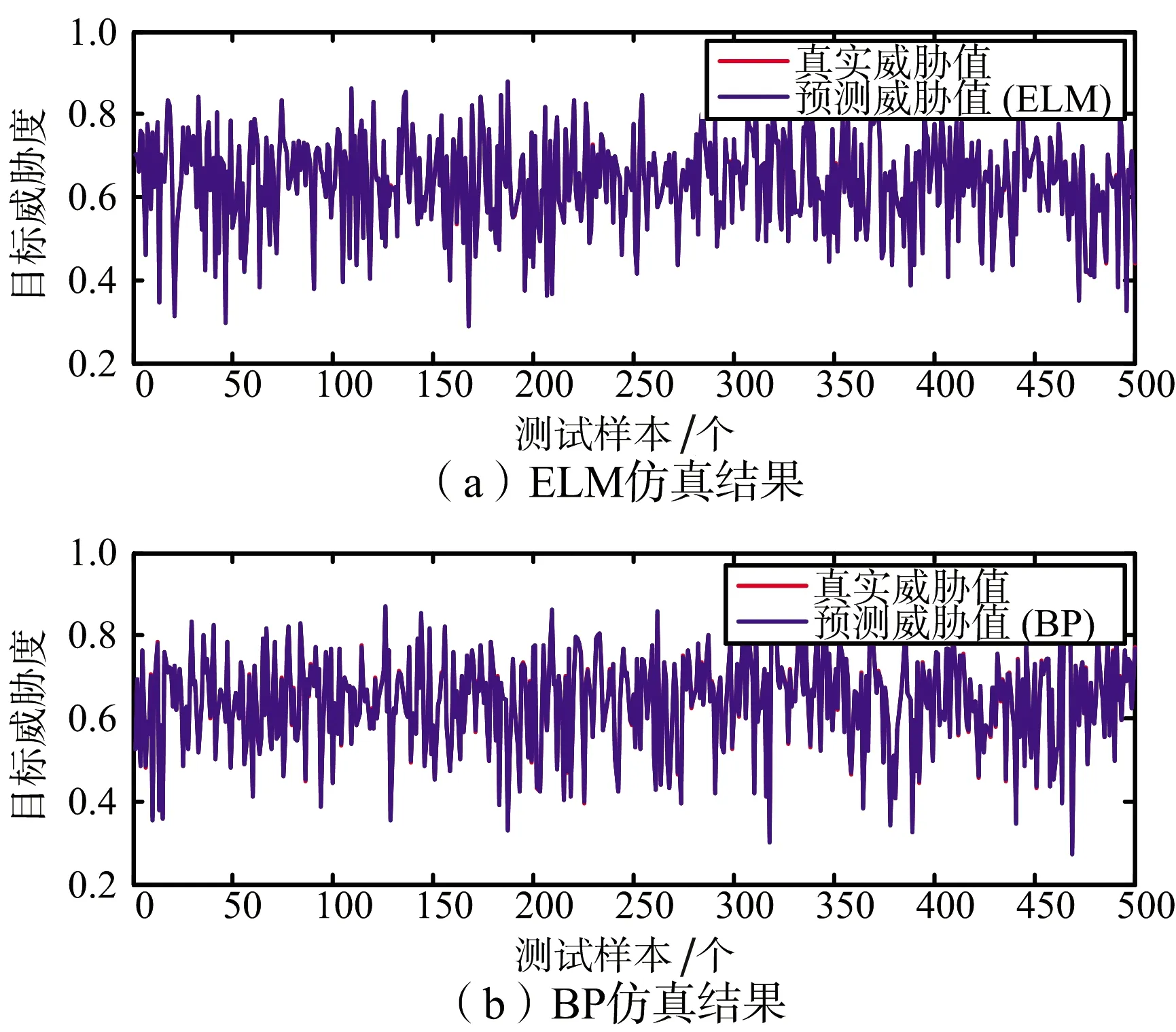
图5 测试样本目标威胁估计结果(500组)

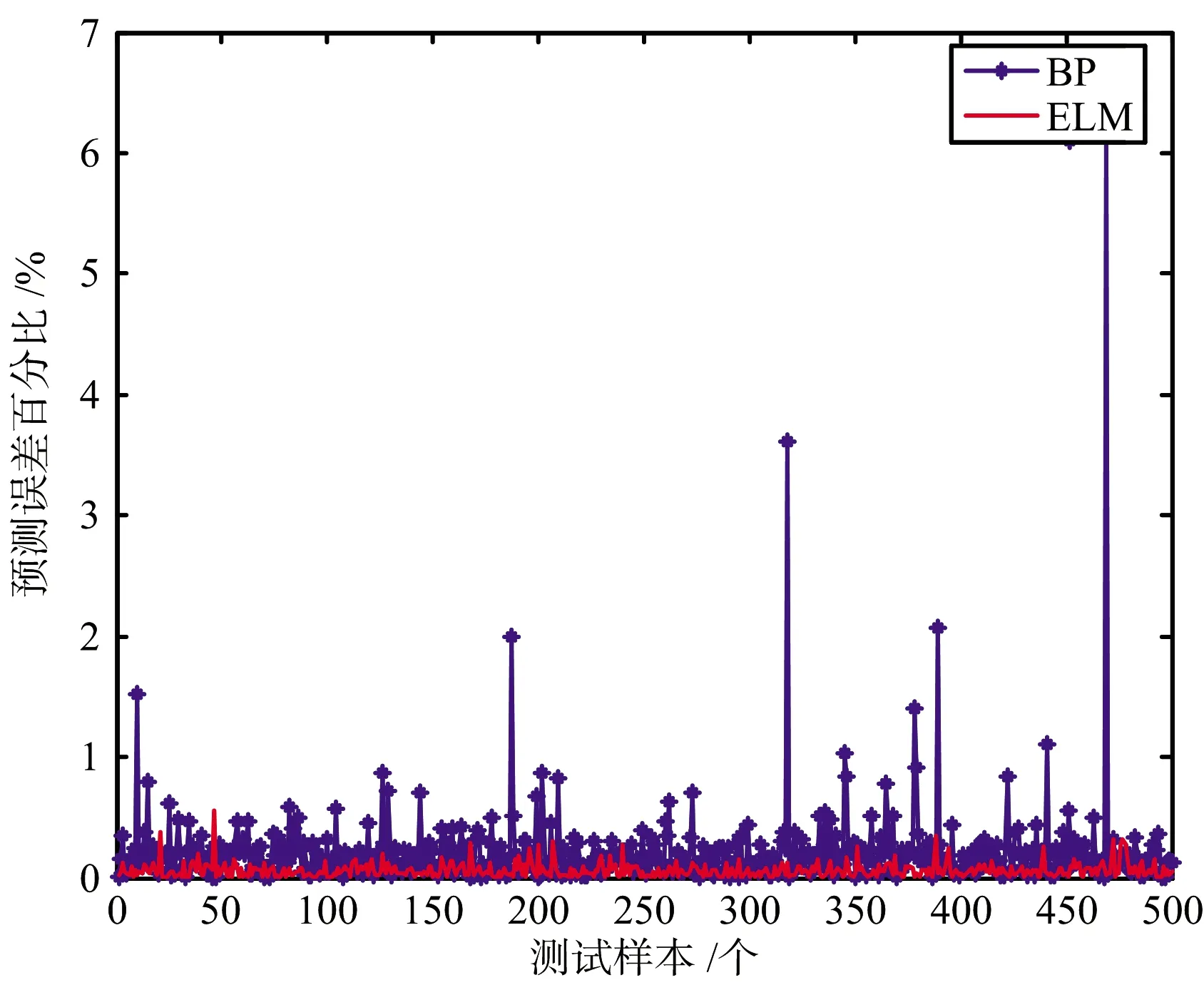
图6 目标威胁估计误差百分比(500组)

选定1 250组样本数据进行模型训练，1 000组数据作为测试，测试结果如图7和图8所示。ELM和BP的预测均值误差分别为7.02×10-4和1.87×10-3。

从以上三组仿真结果对比来看，不同数量的训练样本和测试样本下ELM算法均具有较高的威胁感知精度。为验证算法的学习速度和实时性，通过进一步的仿真，得到基于两种算法进行目标威胁感知的对比结果，如表3所示。可以看出在不同的训练样本数量下，ELM训练出的感知模型均具有较高的估计精度，相较于BP算法存在一个量级上的精度提升；而且更为重要的是，在同等训练样本数目下，ELM的训练时间要比BP算法低一到两个数量级，这对于实时性要求很高的威胁感知系统非常重要。

图7 测试样本目标威胁估计 (1 000组)

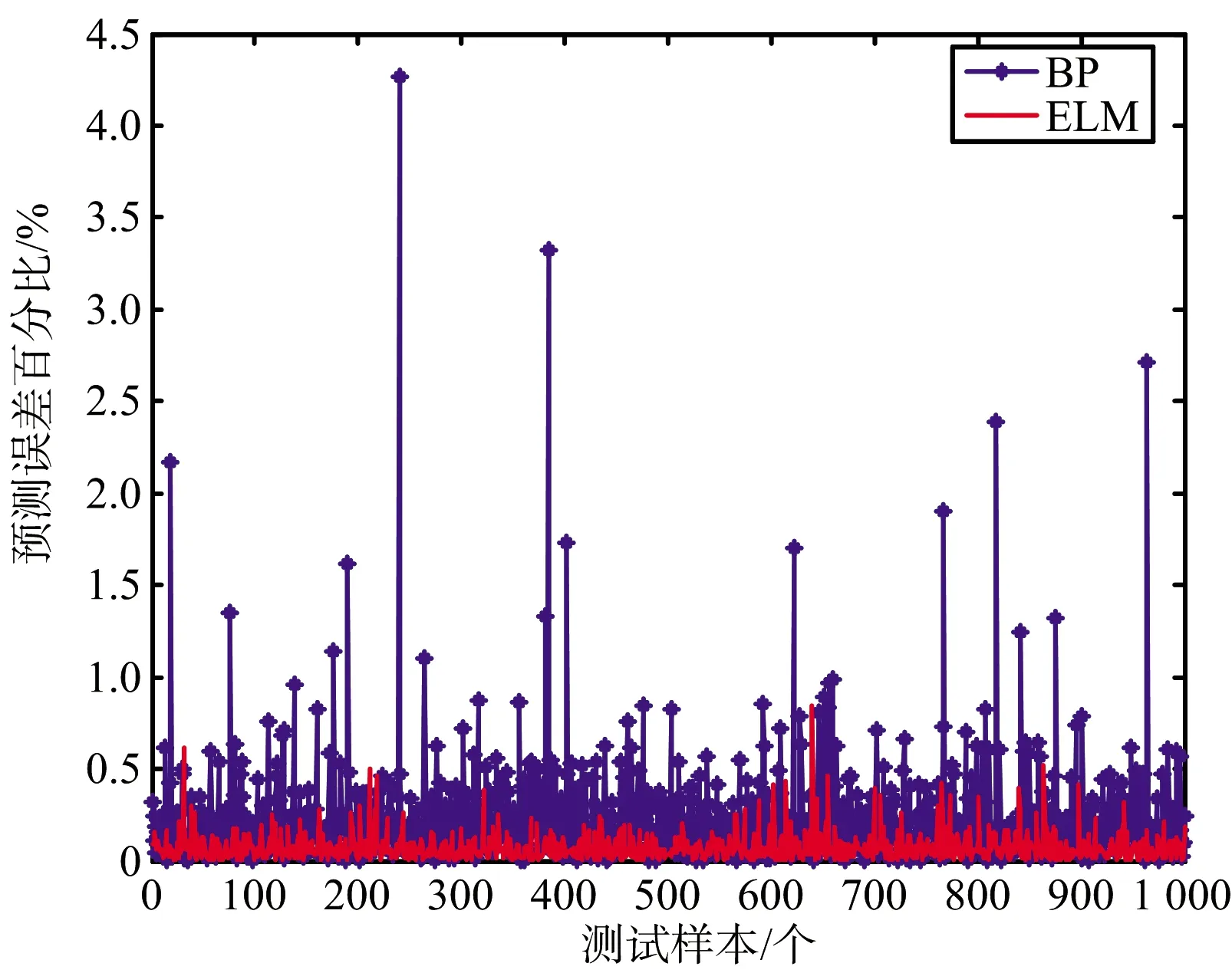
图8 目标威胁估计误差百分比(1 000组)

表3 BP和ELM算法对比

5 结束语

空中目标威胁感知是空战中作战决策的关键依据，涉及的态势因素众多且融合逻辑复杂。本文基于专家知识综合考虑空中目标的特点、类型以及威胁属性多重因素，并采用一种高性能机器学习算法—极限学习机进行目标威胁估计建模，从而实现空战环境下各类目标威胁度的实时智能感知。通过选取不同数量的测试样本数据，基于ELM算法和BP神经网络算法进行了威胁感知的对比仿真，结果均验证了ELM算法训练出的感知模型具有较高的威胁估计精度和良好的实时性。