基于小波变换的滚动轴承故障诊断

陈科百

摘要：针对滚动体轴承故障诊断的故障频率获取问题，利用小波变换对故障轴承采集的数据进行故障特征频率提取分析。首先根据Harr小波理论，给出基于Harr小波的信号分解与重构算法;然后根据轴承元件之间滚动接触的速度关系建立的方程，求得滚动轴承的特征频率;最后以西储大学的6203-2RS JEM SKF深沟球轴承作为研究对象，对轴承的外圈、滚动体和内圈进行故障诊断，利用MATLAB编写小波变换程序并进行仿真分析。仿真结果表明：利用小波变换可以准确的判断滚动轴承的故障振动信号，得出与轴承理论上特征频率相对应的频率点。

关键词：小波变换;故障诊断;滚动轴承;Harr小波理论;特征频率

0  引言

轴承作为旋转机械系统里重要的元件之一，由于工作条件等原因，轴承经常发生点蚀、腐蚀、磨损、胶合等故障。滚动轴承的状态监测和故障诊断一般以采集的振动信号作为分析对象[1]，这对提高机械系统运行状态的稳定性具有重要作用[2]。

故障诊断中，时频分析方法是一种用来处理非线性和非平稳信号的常用方法，主要有小波变换、短时傅里叶变换、经验模态分解（EMD）、固有时间尺度分解（ITD）等[3-5]方法，能够同时时域和频域两个方面来揭示采样信号的成分，从而实现机械系统的故障检测。

针对深沟球轴承故障信息诊断的问题，本文基于Harr小波理论，在其数学模型原理的基础上，给出基于Harr小波的信号分解与重构的算法。根据轴承元件间滚动接触的速度关系建立的方程，求得滚动轴承外圈、内圈、滚动体和保持架的特征频率，以西储大学提供的6203-2RS JEM SKF深沟球轴承进行MATLAB仿真，得出轴承的故障信号时域波形，与特征频率进行匹配，验证模型的正确性。

1  信号分解与重构

基于Harr小波的信号分解与重构过程主要分为以下四步：

2  滚动轴承运动产生的特征频率

滚动轴承的特征频率可以根据轴承元件间滚动接触的速度关系建立的方程求得。滚动轴承主要由外圈、内圈、滚动体和保持架四部分组成。轴承节径（滚动体中心所在的圆）为D，滚动体直径为d，个数为Z，接触角为？琢。

为分析轴承各部分运动参数，先做如下假设：

①轴承承受轴向和径向载荷时各部分均无变形;

②轴承的内外圈与滚动体之间无相对滑动;

③外圈滚道旋转频率为fO;

④内圈滚道旋转频率为fi;

⑤保持架旋转频率为fc。

3  滚动轴承故障诊断仿真

3.1 滚动轴承故障测试数据

待检测的轴承支承着电动机的转轴，驱动端轴承型号为SKF6205，风扇端轴承型号为SKF6203，表1中列出了两种轴承的几何尺寸和各部件的故障频率。轴承用电火花加工单点损伤，损伤直径分为4种：0.007英寸=7mils=0.1778mm，0.014英寸=14mils=0.3556mm，0.021英寸=21mils=0.5334mm，0.028英寸=28mils=1.016mm（1英寸=25.4mm）。其中，轴承外圈的损伤点在时钟的3点钟、6点钟和12点钟三个不同的位置进行设置。滚动体个数Z=8个，其具体的尺寸数据如表1所示。

将表1中的参数带入公式（1）～（13），并结合西储大学官网给出的参数，可得到6203-2RS JEM SKF 深沟球轴承在转速n=1750r/min时各部分的故障频率，如表2所示。

3.2 MATLAB小波变换故障诊断仿真

在本文中，我们以型号为6203-2RS JEM SKF 的深沟球轴承作为研究对象，研究其在损伤直径为0.007英寸、外圈损伤点在时钟的6点钟、转速n=1750r/min、采样频率为12kHz时的故障诊断信号。对下载后的数据导入MATLAB进行處理，通过MATLAB编写小波变换程序，检测轴承的外圈、内圈和滚动体的故障频率。

3.2.1 轴承外圈小波变换故障诊断仿真

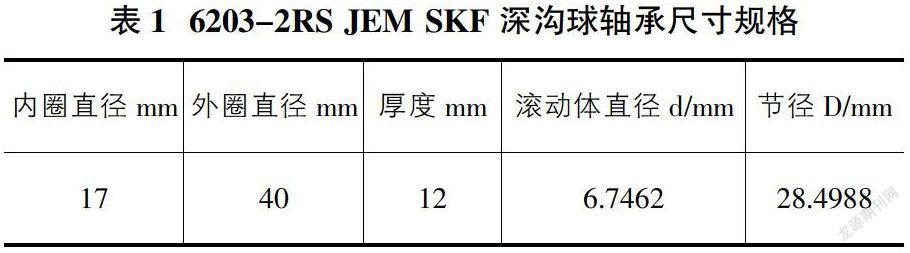
采集的轴承外圈故障振动信号时域波形如图1所示，从波形上我们看不出轴承的外圈是否存在故障。

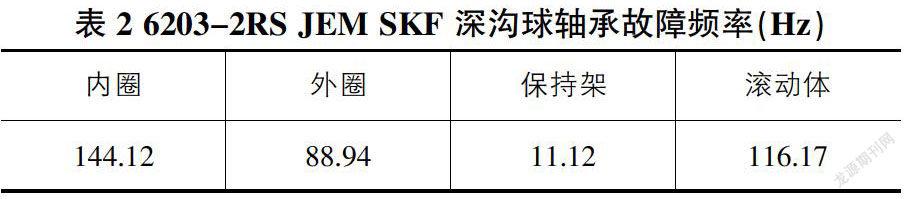
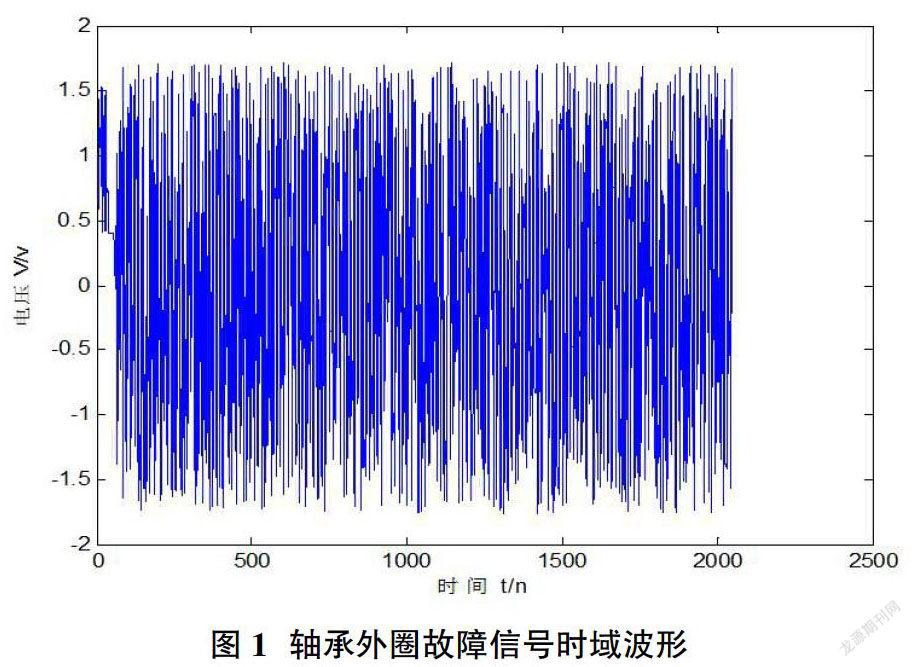
对图1中的信号用db10正小波基进行4层小波分解，分解结果如图2所示，其中d1～d4分别表示第1、2、3、4层细节信号。为了提取外圈故障特征频率，进一步对第1层细节信号d1做Hilbert包络并进行谱分析，结果如图3所示。从功率谱的分析可以发现频率87.89Hz的存在，对比表2轴承故障特征频率可以发现，轴承的外圈发生了故障。

3.2.2 轴承滚动体小波变换故障诊断仿真

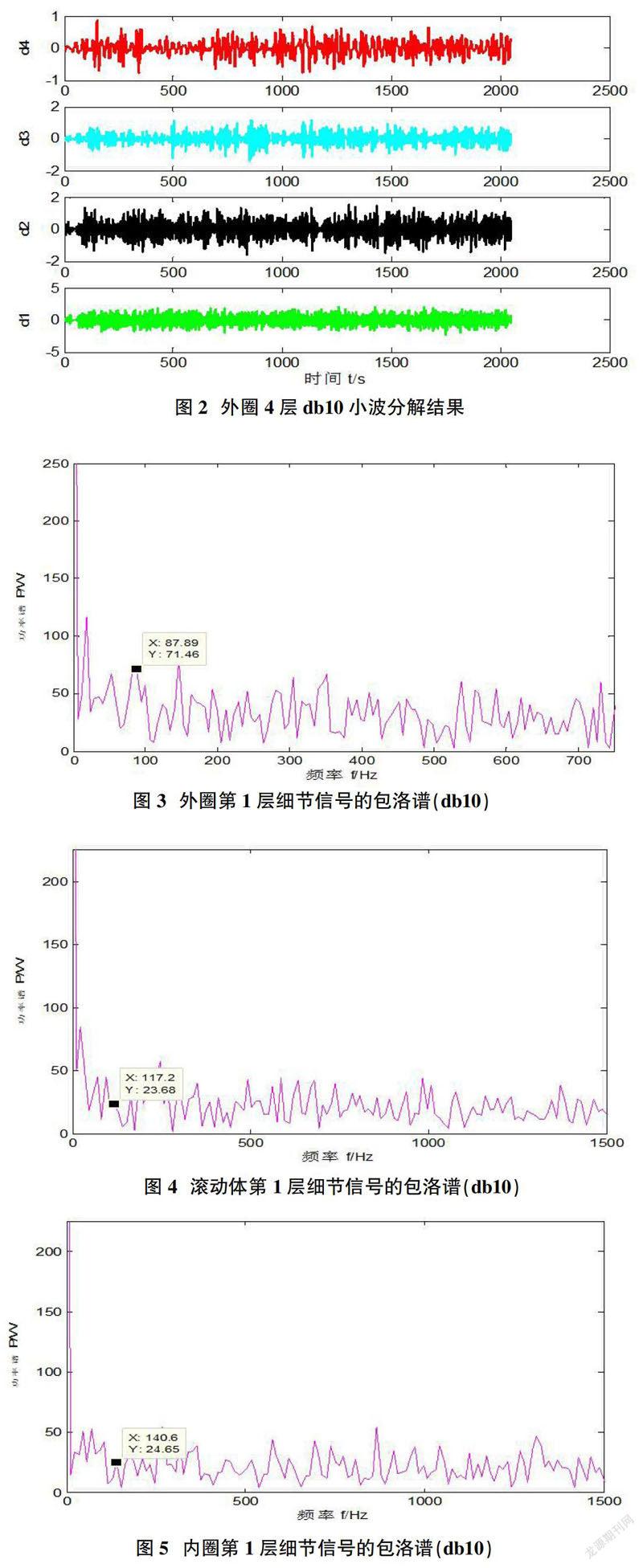
同上一节，从采集的轴承内圈故障振动信号时域波形上我们看不出轴承滚动体是否存在故障，通过其信号用db10正小波基进行4层小波分解，然后进一步对第1层细节信号d1做Hilbert包络并进行谱分析，结果如图4所示。从功率谱的分析可以发现频率117.2Hz的存在，对比表2轴承故障特征频率可以发现，轴承的滚动体发生了故障。

3.2.3 轴承内圈小波变换故障诊断仿真

同上，从采集的轴承内圈故障振动信号时域波形上我们看不出轴承的内圈是否存在故障。

对其信号用db10正小波基进行4层小波分解，然后进一步对第1层细节信号d1做Hilbert包络并进行谱分析，结果如图5所示。从功率谱的分析可以发现频率140.6Hz的存在，对比表2轴承故障特征频率可以发现，轴承的内圈发生了故障。

4  结论

①本文针对滚动体轴承故障诊断时故障频率获取问题，首先给出基于Harr小波的信号分解与重构算法，然后根据轴承元件之间滚动接触的速度关系建立的方程，求得滚动轴承的特征频率。

②仿真结果表明：利用小波变换可以准确的判断滚动轴承的故障振动信号，其中外圈功率谱中存在87.89Hz的频率，滚动体功率谱中存在117.2Hz的频率，外圈功率谱中存在140.6Hz的频率。

③三个频率均与表2给出的轴承特征频率相对应，但是由于测试误差和计算误差的存在，三个频率与理论的特征频率存在细微波动。

参考文献：

[1]余建波，吕靖香，程辉，等.基于ITD和改进形态滤波的滚动轴承故障诊断[J].北京航空航天大学学报，2018，44（2）：241-248.

[2]石晓辉，阳新华，张向奎，等.改进的形态差值滤波器在滚动轴承故障诊断中的应用[J].重庆理工大学学报（自然科学），2018，32（1）：1-6.

[3]FREI MG， OSORIO I. Intrinsic time-scale decomposition： Time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society A： Mathematical， Physical and Engineering Sciences， 2007， 463（2078）：321-342.

[4]张琳，黄敏.基于EMD和切片双谱的轴承故障诊断方法[J].北京航空航天大学学报，2010，36（3）：287-290.

[5]HUANG NE， SHENZ， LONG SR， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A： Mathematical， Physical and Engineering Sciences，， 1998， 454（1971）：903-995.