某二阶偏微分方程计算方法对比分析
贾涛 牛华东 解景涛 卢瑞军 苏茂辉

摘要:CAE在汽车和发动机设计中发挥越来越重要的作用,然而CAE的本质是求解各种常微分方程组或偏微分方程组;常微分方程又称动力系统方程,通常用来求解动力系统问题。偏微分方程则广泛应用于电磁学、流体力学、结构力学等多个领域;对于偏微分方程通常很难求得其解析解,需要借助数值计算来获取其方程的近似解。拉普拉斯方程(Laplace)是一种椭圆形二阶偏微分方程,并且可以求取其解析解。本文通过解析法以及数值法对拉普拉斯方程求解,并对比不同求解方法的效率和精度;结论显示解析法虽然精度较高,但是需要很大的计算量,并且大多数偏微分方程没有解析解。因此,在汽车和发动机等工程应用中应该根据精度需求选择最优的途径求解偏微分方程问题。
关键词:Laplace方程;偏微分方程;数值计算;CAE
1 理论分析
拉普拉斯方程的数学表达式如下,
2 问题描述
研究某矩形二维传热问题,已知传热问题的导热微分方程式如下[2]:
3 解析解
求解偏微分方程的核心在于边界条件,不同的边界条件甚至会出现完全不同的解;根据该问题描述,通过边界条件将上述方程简化:
由于公式(5)比较繁琐,并且涉及到n(0~∞)求和计算;方程组规模小则计算量小,可以快速得到计算结果;方程组规模大则计算量很大,通常需要很久才能完成计算。本例中算法1取n=110,对5000个数据编程计算,则耗时近1小时;而采用算法2则只需要数秒时间。
算法1:
clc;
clear;
sum=zeros(100,50);
syms x;
for i=1:100;
for j=1:50;
for k=1:110;
Dn=int(100*sin(k*pi*x/50),0,50);
An=1/(25*sinh(2*pi*k));
Cn=sinh(k*pi*(100-i)/50);
Bn=sin(k*pi*j/50);
Un=Dn*An*Cn*Bn;
sum(i,j)=sum(i,j)+Un;
end
end
end;
算法2:
clc;
clear;
sum=zeros(100,50);
for i=1:100;
for j=1:50;
for k=1:110;
Dn=5000*(1-cos(k*pi))/(k*pi);
An=1/(25*sinh(2*pi*k));
Cn=sinh(k*pi*(100-i)/50);
Bn=sin(k*pi*j/50);
Un=Dn*An*Cn*Bn;
sum(i,j)=sum(i,j)+Un;
end
end;
end;
4 數值解法
通过数值方法求解偏微分方程是常用的求解方法,如下通过有限元方法以及EXCEL迭代、软件编程等不同方法进行数值计算,对比不同计算方法的精度和计算效率。
4.1 有限元方法
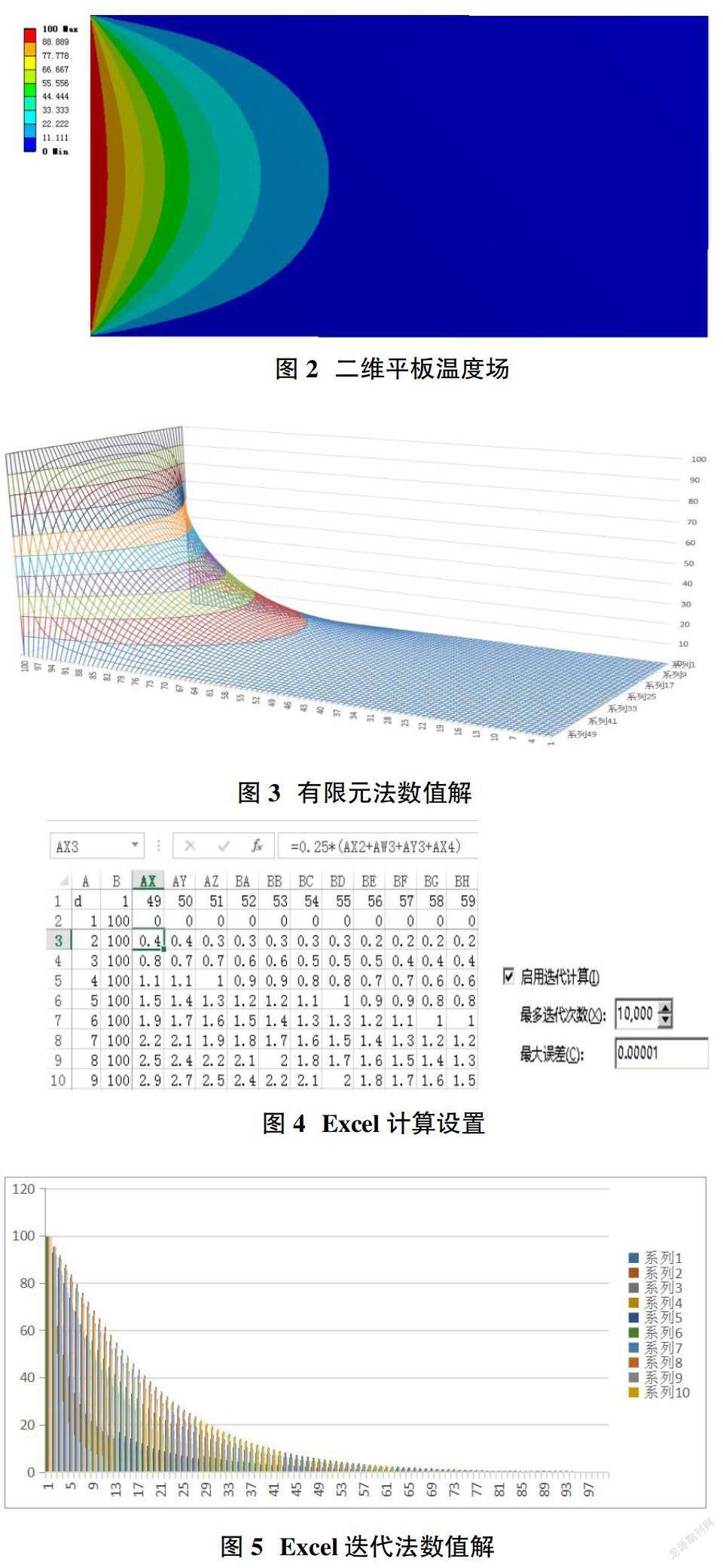
借助有限元软件,建立平面模型并搭建稳态热力学模型,生成5151个节点、10000个单元;设置边界条件如上所述,计算得到的温度场分布如图2所示:该方法更偏向于工程的应用。在求解过程中,模型搭建过程花费较多时间;但是求解计算效率较高,普通电脑计算只需要20sCPU时间。
4.2 Excel迭代方法
设置步长dx=dy=1,采用五点差分法求解;如图4所示,使用EXCEL建立数值计算表格,启用迭代计算,设置误差以及最大迭代次数进行求解;该方法计算效率较高,只需要1~2s CPU时间;得到计算结果如图5[3]。
4.3 软件编程计算
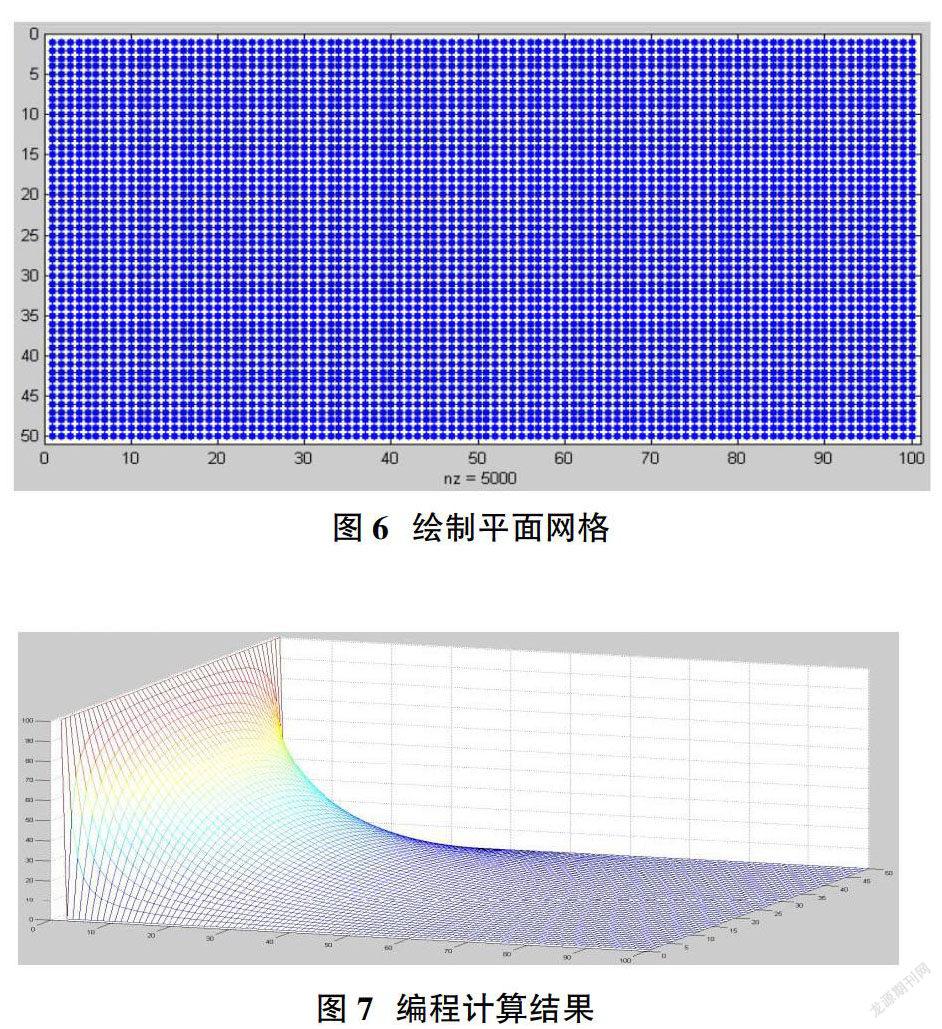
借助软件编写五点差分程序,使用高斯赛德尔迭代法,同样可以计算出最终的结果;编程耗时较长,计算耗时60s左右的CPU时间[4]。
计算程序:
clear
clc
u=1:1:50;
v=1:1:50;
[x,y]=meshgrid(u,v);%通过坐标轴点在平面画网格
p=[x,y];
plot(p);
spy(p);
for i=2:50
for j=2:100
p(i,j)=(j-1)+98*(i-2);
end;
end;
for i=1;
for j=1:100
p(i,j)=0;
end;
end;
for i=50;
for j=1:100
p(i,j)=0;
end;
end;
for j=1;
for i=1:50
p(i,j)=0;
end;
end;
for j=100;
for i=1:50
p(i,j)=0;
end;
end;
PP=delsq(p);
load('my.dat');
b=spconvert(my);
N=length(b); %Gauss – Seidel迭代法
u=inv(PP)*b;
u=zeros(N,1);%迭代初始值
D=diag(diag(PP));
E=-tril(PP,-1);%下三角
F=-triu(PP,1);%上三角
B=inv(D-E)*F;g=inv(D-E)*b;
eps=0.000001;
for k=1:10000 %最大迭代次数
y=B*u+g;
if norm(u-y)<eps
break;
end
u=y;
end
s=zeros(50,100);
for i=1:48
for j=1:98;
s(i+1,j+1)=u(98*(i-1)+j,1);
end
end
for i=1:50
s(i,1)=100;
end
subplot(1,1,1);
mesh(s);
5 误差分析
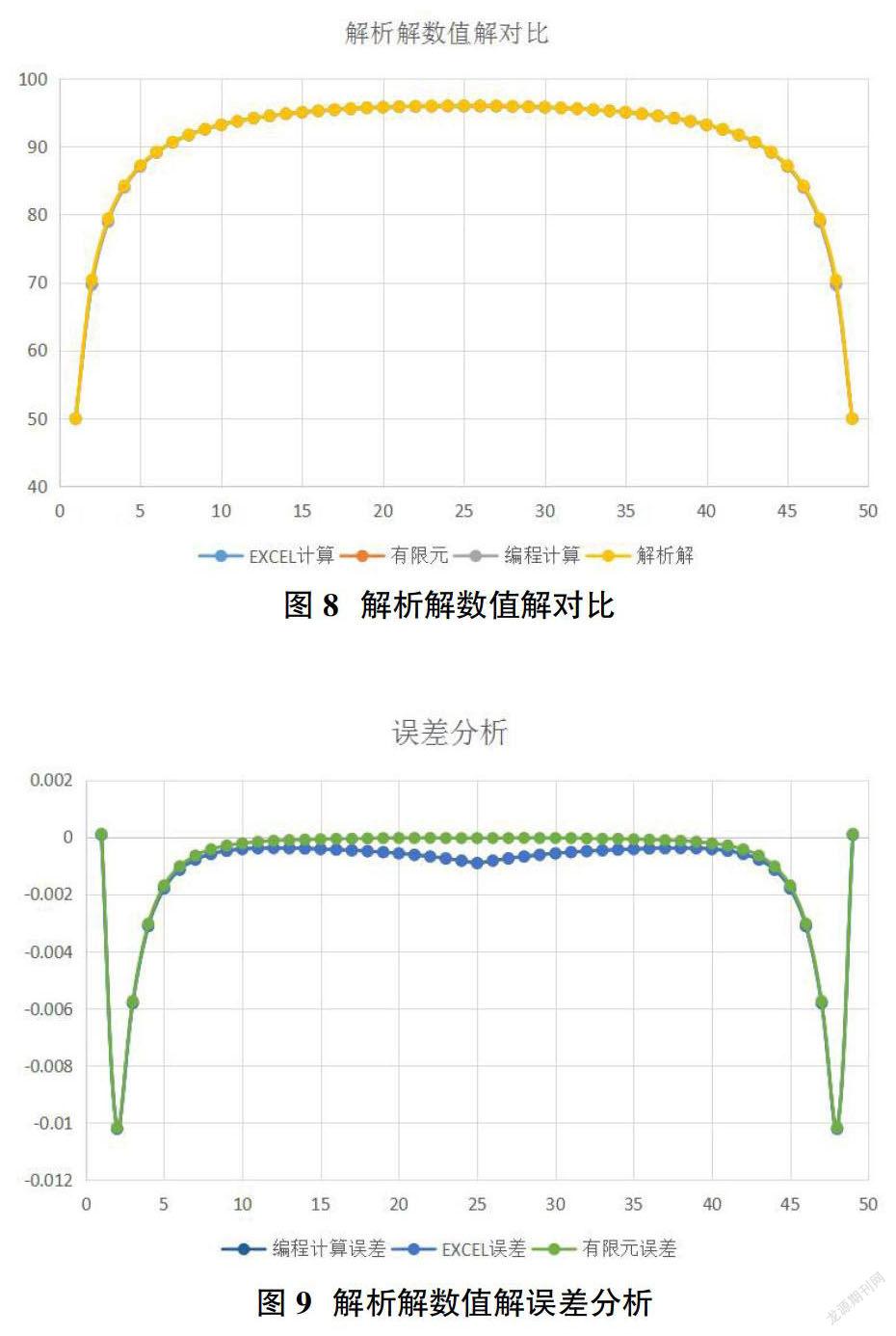
对比计算结果第二列(x=1,u(x,y))数据并绘制图表;如图8所示,数值解和解析解的四条曲线重合在一起,说明这些数值大小相同,整体趋势一致。图9误差分析显示,EXCEL和编程计算误差重合在一起,误差在0~0.01%之间;有限元计算在中间部分误差接近0,说明其计算误差相对较小;三种数值计算方法误差在工程可以接受的范围内。
6 总结
本文通过不同方法求解偏微分方程,对偏微分方程的求解思路有了深入的理解;各种解法中,效率最高的是使用EXCEL迭代求解,操作简单并且计算速度快、精度较高。借助软件编程的方法求解效率相对较低,并且需要对程序调试,精度方面和EXCEL求解差别不大。借助有限元求解则需要搭建有限元模型,并设置边界条件,计算效率同样很高,精度方面可以满足工程需要。而解析法求解拉普拉斯方程雖然精度高,但是对算法要求较高。因此,对于偏微分方程工程方面应用,在满足精度的前提下,解析解不一定是最优的方法;具体需要根据实际情况选择相应的求解方法。
参考文献:
[1]陆金甫,关治.偏微分方程数值解法[M].清华大学出版社,2004.
[2]杨世铭,陶文铨.传热学[M].四版.高等教育出版社,2006.
[3]贾新民,严文.有限差分法求解拉普拉斯方程[J].昌吉学院学报,2009.
[4]刘大卫,高明.正方形环域Laplace方程的简明数值解法[J].沈阳师范大学学报,2006.

