尾矿坝失稳溃决影响数值分析
于家傲 沈振中 杨超 徐力群








摘要:尾矿坝是一种具有高势能的危险源,一旦失稳溃决将对下游居民安全和生态环境造成巨大影响。为预测尾矿坝失稳溃决对下游的影响,以中国某拟建尾矿坝为例,采用极限平衡法估计了尾矿坝失稳的泄沙量,并运用MIKE21 FM软件,建立尾矿坝溃决泄沙的数值模型,计算了尾矿坝失稳后泄沙过程及其影响范围和淹没深度,预测了失稳事故对下游的影响,并提出了相应建议。计算表明,该库溃坝沙流最多可推进到初期坝坝轴线下游2.7 km处。本文方法可应用于尾矿坝溃坝灾害的预测和防治。
关键词:尾矿坝;失稳;溃决影响;淹没深度;数值模拟
一、引言
尾矿坝是指阻挡尾矿浆的尾矿库外围构筑物,泛指初期坝和堆积坝的总体[1]。尾矿坝作为人工修建的高势能危险源,一旦发生溃决,下泄尾沙过程十分迅速,无法对下游居民进行及时地转移和疏散,会带来巨大的经济损失和环境破坏。近年来,世界上尾矿坝溃决事故时有发生,安全形势不容乐观[2]。在工程中设计、施工、管理等因素均会影响坝体的稳定性。尾矿坝发生溃决的原因包括洪水漫顶、坝坡失稳、渗流破坏、结构破坏等[3]。在各种尾矿坝溃决形式中,失稳溃决瞬时性强、诱发因素多,产生的后果较为严重,本文着重对失稳溃决进行研究。
目前,对于尾矿坝溃决的研究方法主要包括经验公式法、模型试验法和数值模拟法。廖威林[4]结合拟建工程对经验公式法和数值模拟法的计算原理和应用方法进行探讨,认为与经验公式法相比数值模拟法可较为合理且更有针对性地模拟尾砂下泄的流动过程;陈俊[5]以马家沟尾矿坝工程为例,采用模型试验法和数值模拟法相结合的分析方法对溃坝尾砂下泄的演进过程做出了详细研究,并提出了相关工程防范措施;张力霆等[6]搭建了尾矿坝溃决的模型试验,并将试验结果分别与数值模拟结果和工程原型资料进行了对比,得到了三种方法所得结果互相吻合的结论。因此数值模拟法应用于尾矿坝溃决研究的合理性已得到充分验证。
在进行尾矿坝溃决的数值分析时,泄沙总量的估计至关重要,它对淹没深度和影响范围等模拟结果具有决定性作用。目前大部分学者对于溃坝时泄沙总量的估计均是假定为尾矿坝某一高程以上的全部或部分堆积体的体积。陈青生等[7]就尾矿坝溃决后下泄沙流对下游的影响提出预测方法,其中泄沙总量取为某一高程以上的全部库容,并将预测结果与实际沙流的影响范围进行比较;高巍[8]利用Fluent软件建立数值模型对某尾矿坝溃坝尾砂的运移进行模拟,泄沙总量和模式假设为尾矿库全库的瞬时全部溃决,并由此对下泄沙流的冲击力、覆盖深度和流动速度进行分析。陈小玉[9]采用数值模拟法对尾矿坝溃决后的尾砂下泄规律进行研究,对于泄沙总量采用假设的方法来确定以简化计算。
可见,上述估计泄沙总量的方法不符合实际情况。实际上,尾矿坝失稳溃决时,仅滑动体是瞬时下滑的,也就是滑动体的体积是泥石流的最大峰值流量。根据边坡稳定性理论,尾矿坝在发生失稳溃决时最有可能的情况即为沿最危险滑动面发生溃决。将最危险滑动面以上堆积体体积作为泄沙总量进行尾矿坝溃决的数值模拟具有更合理的实际意义。
本文以中国湖北省拟建的某磷石膏尾矿库为例,在尾矿坝的边坡稳定分析的基础上,计算了失稳溃决时尾矿库的下泄沙流量,并模拟溃坝沙流的演进过程,得到了下游的淹没深度和影响范围,成果对认识该尾矿坝失稳溃决沙流运动引起的灾害严重程度以及指导下游灾害防治等工作具有重要意义。
二、尾矿坝失稳泄沙量计算
尾矿坝失稳溃决的客观原因是外界环境作用导致尾矿库应力场与渗流场变化,包括滲流场直接诱发边坡失稳、尾矿坝坝基破坏、洪水漫顶溃决等。其中,渗流场作用下发生的失稳溃决往往与浸润线埋深过小有关,此时坝体材料强度参数较低、孔隙比较大,其引发的破坏具有历时短、泄沙量大、沙流演进迅速、冲击强度大等特点,易对下游一定范围内造成严重危害。
(一)边坡稳定计算方法
极限平衡法是边坡稳定性分析应用最多的数值方法,原理简单且结果可信,只需考虑静力平衡条件和Mohr-Coulomb准则,即
式中:τf为土体抗剪强度;c’为土体粘聚力;σ、σ’分别为土体的总应力和有效应力;φ’为土体内摩擦角;Kf是抗滑稳定安全系数;τ为剪应力。
实际应用时,极限平衡法可分为Morgenstern-price法、瑞典条分法、janbu法、不平衡推力法以及Bishop法等,其计算原理如下[10]。
1.瑞典条分法
瑞典圆弧滑动法是最简单又最为古老的条分法,它将滑移面假定为圆柱面,不考虑土条两侧的作用力,其边坡稳定性系数计算公式为:
式中:li为土条底部总长度;Wi为土条重力;αi为土条底部倾斜角。
2.简化毕肖普法
简化毕肖普法考虑了土条之间法向力,其边坡稳定性系数计算公式如下:
式中:Qi为土条水平作用力;ei为滑弧圆心至土条中间的距离;R为滑弧半径;bi为土条宽度;mαi为待定系数,需试算确定。
3.杨布法
杨布法假定条间合力作用于土条底面向上1/3高度处,其边坡稳定系数计算公式如下:
式中:∆Xi为土条两侧切向作用力的增量。
4.Morgenstern-price法
Morgenstern-price极限平衡方法在简化毕肖普方法的基础上考虑土条间切向作用力,滑弧和土条力如图1所示,其边坡稳定性系数计算公式如下:
式中:N为土条底部法向力;D为线荷载;β、ω均为几何参数。
对于尾矿坝,由于材料物理力学性质具有特殊性,条间切向力不宜忽略,故该法的效果较好[11]。
尾矿坝坝坡稳定分析可采用Geo-Studio专业软件,它包括边坡稳定性分析(SLOPE/W)和地下水渗流分析(SEEP/W)等模块,各模块均在同一环境下运行,且模拟时仅需建立一个几何模型即可进行各模块的分析[12]。首先对尾矿坝采用SEEP/W模块进行渗流分析,得到坝体渗流场和浸润线;然后将所得结果作为父项输入SLOPE/W模块进行边坡稳定分析,采用极限平衡法,得到尾矿坝的边坡稳定系数和最危险滑动面。
(二)失稳瞬时泄沙量
采用以上几种条分法,即可通过枚举、试算等方法搜索边坡稳定系数最低的最危险滑动面,确定安全系数。然后根据坝体典型剖面最危险滑动时所得的各土条面积,乘以对应的坝体长度,求和后即可估算出坝体发生失稳滑动时下泄的尾矿砂体积,即失稳瞬时泄沙量。
三、溃坝沙流演进数值模拟
(一)基本假定
溃坝沙流演进数值模拟计算采用以下基本假定:
1.尾矿坝体是可忽略内部变形的刚性材料。
2.发生失稳滑动时尾矿坝各区域材料均呈饱和状态。
3.发生失稳破坏时滑动土体在各力作用下是准静态平衡的。
4.尾矿砂属于黏性不可压缩流体,是各向同性的连续介质体。
5.尾矿砂的流动符合宾汉流动模式,剪应力与剪应变为线性关系,存在屈服应力。
(二)控制方程及计算程序
溃坝泄沙的流动控制方程建立在基于Boussinesq和流体静压假定的不可压缩雷诺平均N-S方程的基础上,由下述连续方程和动量方程描述[13]。
式中:t为时间;x、y为笛卡尔坐标;η为水面高度;d为静水深;h为总水深;f为科里奥利参数;g为重力加速度;ρ为水的密度;sxx、sxy、syx和syy分别为辐射应力张量的分量;s为点源流量值;分别为x、y方向上的速度分量;Tij为侧向应力。
计算程序采用由丹麦水力研究所开发的MIKE Zero软件,该软件具有用户界面友好、处理功能强大、可定义多种类型边界条件等优点,其中的MIKE21 FM水动力模块可进行尾矿坝失稳溃决的泄沙影响数值分析,即结合基本假定,通过尾矿坝发生失稳滑动时的下泄体积、尾矿砂的物理力学参数等已知条件求解计算,模拟溃决尾砂的演进过程、淹没高度和淹没范围,从而分析溃坝对下游的影响。
(三)计算步骤
运用极限平衡法及Geo-Studio软件、MIKE21 FM软件,尾矿坝失稳溃决影响数值分析的计算步骤如下。
1.进行尾矿坝渗流分析,根据尾矿坝各部分渗透系数,通过Geo-Studio软件的地下水渗流分析模块(SEEP/W)确定尾矿坝渗流场和浸润线。
2.进行尾矿坝坝坡稳定性分析。采用极限平衡法,以SEEP/W模块的渗流分析结果作为父项建立SLOPE/W边坡稳定模型,确定最危险滑动面。
3.計算尾矿坝失稳最危险滑动面对应的溃决下泄堆积体体积。
4.将研究范围内的地形信息导入MIKE Zero中,确定模型边界线并生成单元网格,设置干湿边界、糙率和涡黏系数等参数。
5.设置模型初始条件和边界条件,将步骤3得到的下泄体积和流量过程线作为上边界导入MIKE21 FM水动力模型中,并根据地形实际设定下游开边界。
6.在尾矿坝下游选取若干敏感点,利用MIKE Zero的Data Extraction FM数值提取工具提取步骤4计算结果中各点淹没深度、沙流流速等信息,并对结果进行分析。
四、工程实例
(一)工程概况
中国湖北省宜都市六里冲磷石膏库,下游约8.6 km为长江,东北侧约2.9 km为岳宜高速。主堆积坝总有效库容约为7729×104 m3,属二等库[1]。该库主坝分两期建设,初期坝均为透水堆石坝,堆积坝采用上游式湿法堆存工艺。其中主坝二期初期坝坝顶标高180 m,坝轴线自然地面标高约145 m,坝高约35 m,顶宽5 m,坝顶长约为186 m,内外坡坡比分别为1∶1.6和1∶1.8;堆积坝由11级高10 m、平均坡比1∶3.5、坝顶设5 m宽马道的堆积子坝组成,最终标高290 m,堆积坝总高145 m。二期主坝下游1 km范围内有居民约35户。沿山谷方向切取尾矿坝典型剖面如图2所示,各区域材料的物理力学参数值如表1所示。
(二)坝坡稳定计算
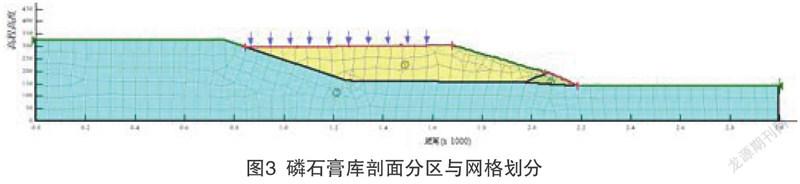
根据典型断面,在Geo-Studio软件中构建二维有限元法渗流分析和极限平衡法边坡稳定分析的模型。尾矿坝剖面材料分区和网格划分情况如图3所示。
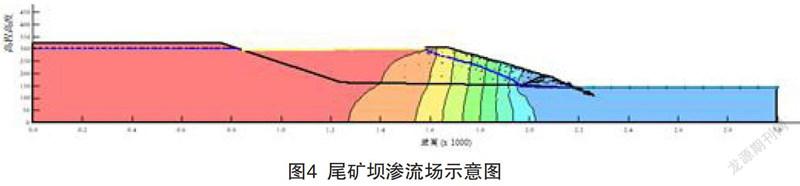
根据假定,在Geo-Studio软件的SEEP/W模块中输入三个材料分区的渗透系数,确定坝体上下游水头值作为边界条件,计算得到渗流场位势分布和浸润线位置如图4所示。
以所得SEEP/W渗流分析结果作为父项,建立SLOPE/W模块的边坡稳定模型,以浸润线位置作为孔隙水压力线,根据表1输入三个材料分区的容重、粘聚力和内摩擦角数值,采用半正弦函数,利用瑞典条分法等极限平衡计算方法,得到尾矿坝最危险滑动面位置和土条情况如图5所示,各方法的边坡稳定系数值如表2所示。
(三)溃坝影响分析模型构建
1. 计算范围及网格划分
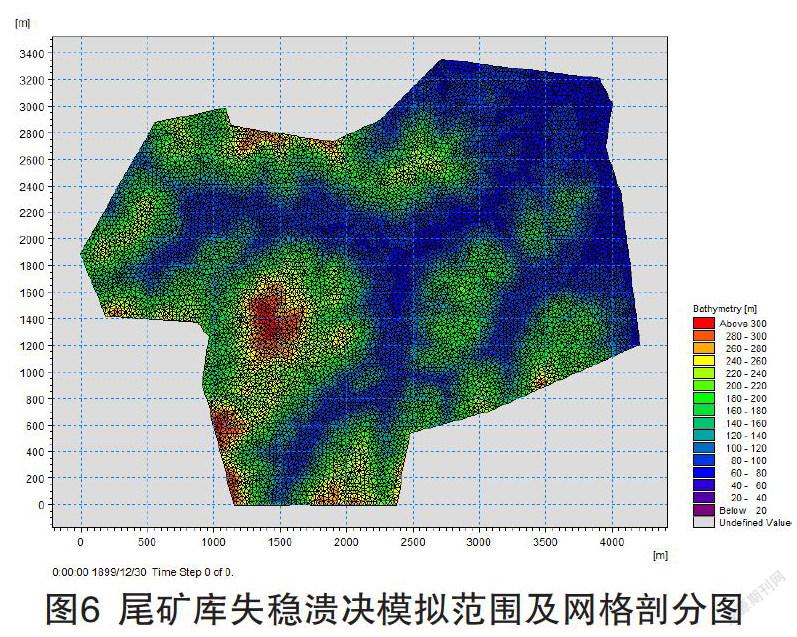
根据尾矿库地形地貌及类似工程经验,溃坝影响分析模型选择自初期坝顶至下游岳宜高速附近的范围进行计算,东西方向约3.5 km,南北方向约3.0 km。采用三角形单元对边界范围内的区域进行划分,网格最大三角形面积不大于28 m2。计算区域网格共有结点数10468个,三角形单元数20511个。尾矿库失稳溃决模拟范围及网格剖分示意图如图6所示。
2.模型参数
计算模型需要确定的参数包括涡黏系数、糙率以及干湿边界等。根据假定及工程经验,涡黏系数采用Smagorinsky公式,设为常数,取值0.28。糙率作为MIKE21 FM水动力模块的一项重要参数,其取值的合理性会直接影响计算结果的精确性[14]。糙率按照经验估值,对于居民区、农田和森林分别取为0.04、0.025和0.06[15]。这里采用曼宁糙率系数,由于曼宁数取值越大,沙流流动性越强,淹没范围越大,安全起见应尽可能取大值,曼宁数确定为1.2。干湿边界的三个控制参数干水深、淹没深度和湿水深分别取0.005 m、0.05 m和0.1 m[16]。除此之外,不考虑科氏力的影响,不计风力、冰盖以及波浪作用。
3.边界条件及初始条件
模型的边界条件包括开边界和陆地边界。开边界的上游条件输入基于最危险滑动下泄体积的流量过程线,下游设置在区域边界上高度相对较低处;其余边界作为陆地边界。初始条件是模拟计算初时刻区域内初始水位和流速的信息。由于尾矿库下游天然流量极小,可忽略不计,故设置初始条件为全区域深度与流速均为0。
4.流量过程线
工程上多用4次抛物线来概化瞬时溃坝的流量过程线,如图7所示,可很好地符合沙流下泄流量变幅大的特点,与实际沙流覆盖范围和厚度吻合。概化的4次抛物线过程如表3所示[17],表中t为任意时刻;T为泄沙时间;Qm为最大泄沙流量;Qt为任意t时刻泄沙流量。
(四)溃決影响分析
根据类似工程经验,设定本次溃决数值模拟过程总时间为30 min,并结合堆积坝范围和边坡稳定计算结果,得到最危险滑动情况下的下泄总量为1343万立方米。依据图7和表3绘制流量过程线如图8所示。
按照上述参数、初始和边界条件取值方法导入MIKE21 FM水动力模型中进行计算即可。
1. 淹没范围计算
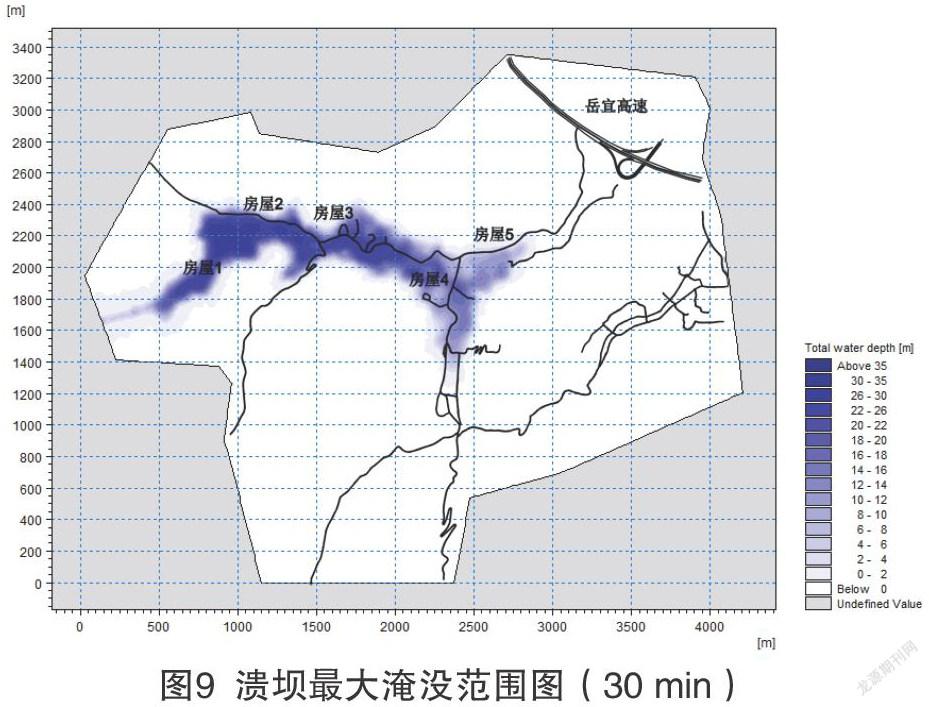
根据磷石膏库周边地形和沙流演进路径,选择下游房屋、道路等需重点保护单位作为敏感点,绘制最大淹没示意图见图9。
由此可见,坝坡失稳溃决时沙流在二期初期坝下游沟谷内淹没深度较大,淤积较多;距坝址越近淹没深度越大。二期工程初期坝下游2 km范围以内的建筑物将被淹没,沙流可推进到初期坝坝轴线下游2.7 km处。
2.下游敏感点淹没深度及流量分析
使用Data Extraction FM工具对图9所示的溃决计算结果进行数值提取,得到各敏感点的淹没深度变化曲线如图10所示;除此之外,还可求得溃坝沙流最大单宽流量、沙流演进过程等信息,如表4所示。
计算结果表明,随着演进时间的增加,各敏感点淹没深度从某一时刻开始出现,并逐渐增大,在期间某一时刻淹没深度达到峰值,之后随沙流继续下泄而又逐渐减小,最后趋于稳定。理论上,尾矿库溃坝后沙流的演进可以概化为增长阶段、稳定阶段和衰减阶段,数值模拟结果符合溃坝沙流演进的理论规律。另外,一般距离坝址越近处,溃坝沙流到达时间越早,淹没深度变化越大,最大单宽流量亦越大。
五、结论
采用数值分析方法,确定了尾矿坝失稳破坏的最危险滑动面,估算了滑动泄沙量,并模拟了溃决泄沙的过程,分析了坝体失稳溃决对下游的影响,取得以下成果。
提出了确定尾矿坝最危险滑动面、坝体失稳泄沙量的计算方法,仿真分析了沙流演进的全过程。
坝坡失稳溃决时沙流在初期坝坝趾处流量大,流速快,淹没深度大,破坏性强。二期初期坝下游沟谷内淹没深度较大,淤积较多,二期工程初期坝下游2 km范围以内的建筑物将被淹没,沙流最多可推进到初期坝坝轴线下游2.7 km处,对下游更远范围的影响可忽略;初期坝坝趾下游150 m至2420 m内的多座房屋将发生淹没情况,而3575 m处的岳宜高速公路不会受到溃坝下泄沙流的影响。
建议采取应对措施:将二期工程初期坝下游1 km左右范围内的居民进行搬迁;确保尾矿库坝坡排洪、排渗系统正常工作,在坝体内埋设监测设备以及时观测变形和浸润线,保持浸润线满足控制要求;采取截流导渗、支挡加固、覆盖植草等各种工程和非工程措施,尽量减小坝坡下滑力、增加坝坡抗滑力。
参考文献:
[1]田文旗,曲忠德,伍绍辉,等.AQ2006-2005.尾矿库安全技术规程[S].北京:中国标准出版社, 2005.
[2]门永生,柴建设.我国尾矿库安全现状及事故防治措施[J].中国安全生产科学技术, 2009,5(01):48-52.
[3]欧自强.金属矿山尾矿坝的溃坝事故及其他有关情况简介[J].勘察科学技术, 1989(02):30-34.
[4]廖威林.尾矿库溃坝尾砂下泄数值模拟研究[D]:[硕士学位论文].广州:华南理工大学, 2015.
[5]陈俊.尾矿库瞬态溃坝下泄砂流演进过程研究[D]:[硕士学位论文].南昌:南昌大学, 2017.
[6]张力霆,齐清兰,李强,等.尾矿库坝体溃决演进规律的模型试验研究[J].水利学报, 2016,47(02):229-235.
[7]陈青生,孙建华.矿山尾矿库溃坝砂流的计算模拟[J].河海大学学报, 1995(05):99-105.
[8]高巍,袁利伟,马龙龙,等.云南某尾矿库溃坝数值模拟研究[J].化工矿物与加工, 2019,48(05):60-64.
[9]陈小玉.尾矿库溃坝下泄尾砂演进数值模拟研究[D]:[硕士学位论文].广州:华南理工大学,2016.
[10]卢廷浩.土力学[M].南京:河海大学出版社,2005,243-257.
[11]孙文杰.基于Morgenstern-price极限平衡法的尾矿坝边坡稳定性分析[J].有色金属(矿山部分), 2018,70(01):101-102.
[12]张红.尾矿坝边坡失稳物理机理及数值仿真方法研究[D]:[硕士学位论文].北京:华北科技学院, 2018.
[13]王乃欣.土石坝溃决溃口数值模拟与溃坝虚拟现实技术研究[D]:[硕士学位论文].北京:中国水利水电科学研究院, 2018.
[14]丁泽浩.MIKE21曼宁数对水域流速模拟影响研究[J].资源节约与环保, 2018(03):30.
[15]郭凤清,屈寒飞,曾辉,等.基于MIKE21 FM模型的蓄洪区洪水演进数值模拟[J].水电能源科学, 2013,31(05):34-37.
[16]毛翼飞,徐力群,史亚旋,等.基于分段模型法的尾矿库溃坝影响预测分析[J].水电能源科学, 2019,37(11):100-103+14.
[17]袁兵,王飞跃,金永健,等.尾矿坝溃坝模型研究及应用[J].中国安全科学学报, 2008(04):169-172.

