“整体与部分关系原理”在解函数综合题中的应用

李永革

摘 要：数学解题需要高观点指导，整体与部分关系在数学课程中普遍存在.利用“整体与部分关系原理”解函数综合题，可通过抓关键点与关键部分;抓整体结构;合理分拆与变换;整体与部分性质的统一;部分性质有机结合来实现.

关键词：整体与部分;关系;函数综合题;应用

中图分类号：G632      文献标识码：A      文章编号：1008-0333（2020）16-0044-03

数学学习，应该从“知识的积累”上升到“处理问题的一般方法”，挖掘背后蕴含的丰富思想，形成看问题的基本观点.布鲁纳在《教育过程》的“结构的重要性”中希望学生的学习从“特殊”迁移上升到“原理和态度”的迁移，即学习一个一般观念.观念决定视野，视野决定格局，格局决定境界.观念是思想的升华，决定了看问题的深度和层次.因此，数学解题不能仅仅限于“解”和“题”，需要高观点的指导.

函数是描述事物变化规律的数学模型，从“形”来看，函数图象上的点是部分，整个图象是整体;从“数”来看，定义域是整体，属于定义域的任意一个实数或区间是部分;从“表达式”来看，解析式是整体，其中的局部单元是部分，运用“整体与部分关系原理”指导函数问题解决，会产生意想不到的效果.

一、原理的内容

1.内涵

整体是构成事物诸要素的有机统一，部分是整体中的某个或某些要素.

2.整体与部分辩证关系原理的方法论意义

（1）整体的地位作用其方法论意义

整体具于主导地位，统帅着部分，拥有部分所不具备的功能.我们应当树立全局观念，立足于全局，统筹整体，选择最佳方案，实现整体的最优目标.从而达到整体功能大于部分功能的理想效果.

（2）部分的地位作用及其方法論意义

整体是由部分构成的，关键部分功能及其变化甚至对整体起决定性作用.我们必须重视部分的作用，搞好局部，用局部的发展来推动整体的发展.

二、原理的应用

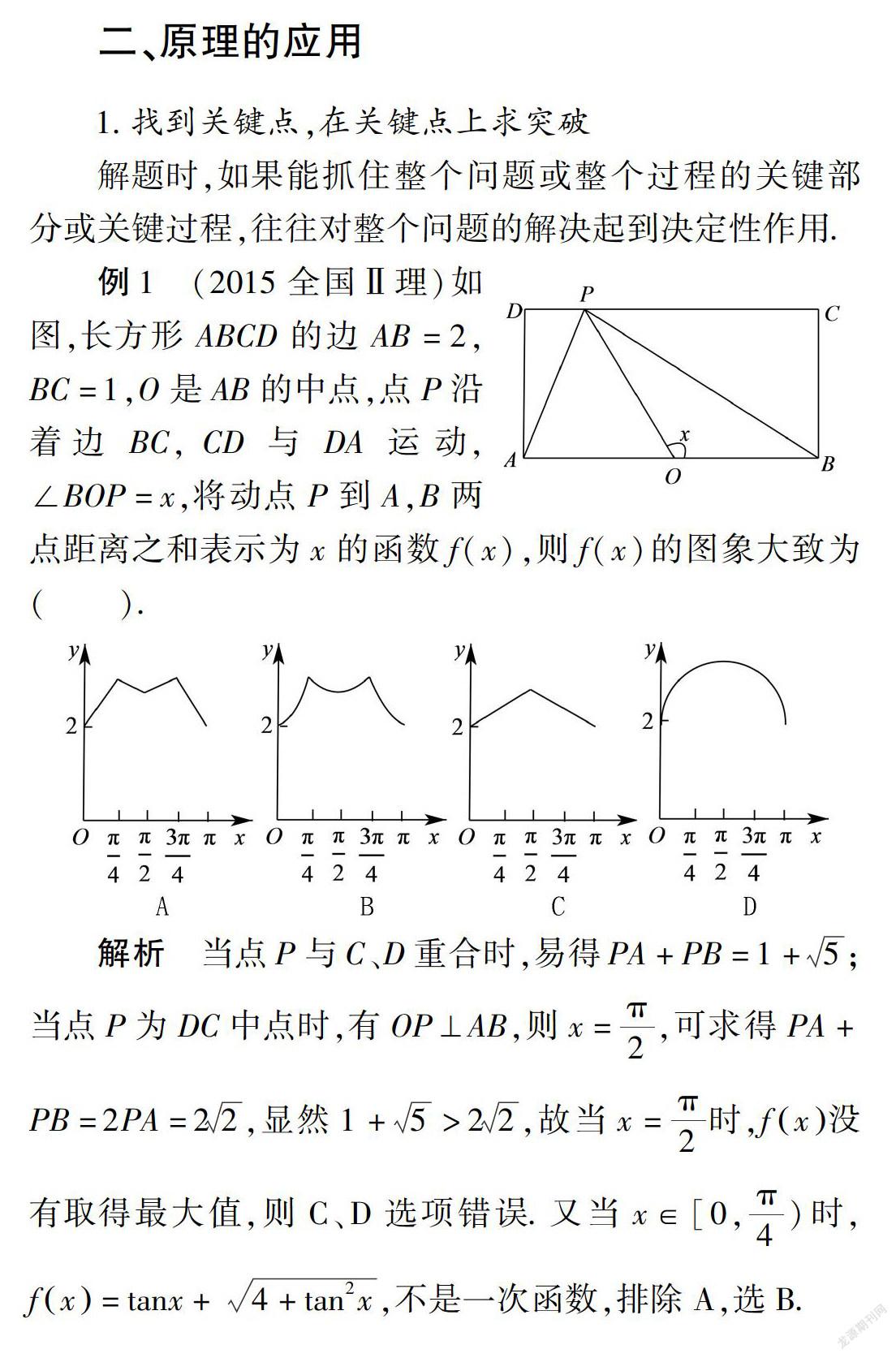
1.找到关键点，在关键点上求突破

解题时，如果能抓住整个问题或整个过程的关键部分或关键过程，往往对整个问题的解决起到决定性作用.

以上结合实例探讨了“整体与部分关系原理”在解答函数综合题中的运用.事实上在数学课程中，能够用“整体与部分关系原理”来思考的问题还很多，比如：统计学中的用样本估计总体，平几中的图形分解，立几中的截面选取，代数中利用函数观点研究方程、不等式、数列等等.只要我们善于利用上述原理思考，都会有助于思维的突破.

参考文献：

[1]吕荣春.高观点下全国卷高考数学压轴题解题研究三部曲[M].成都：电子科技大学出版社，2019.

[责任编辑：李 璟]