波罗的海干散货运价指数与中国制造业PMI相关性研究

余庚哲

摘要：波罗的海干散货运价指数作为全球经济的缩影，而中国制造业PMI作为我国制造业的“晴雨表”，研究两者之间的关系将对企业和政府决策有一定的参考价值。选取2005年1月至2020年4月的中国制造业采购经理人指数（PMI）月度数据和波罗的海干散货运价指数（BDI）月度数据构建VAR模型，进行格兰杰因果检验、脉冲响应分析和方差分解。结果表明在短期内，中国制造业PMI和BDI的影响是单向的，中国制造业PMI的变化对BDI的影响并不显著，而BDI却是带动中国制造业PMI变动的格兰杰原因，且影响较为显著。

关键词：BDI;制造业PMI;VAR模型

波罗的海干散货运价指数（BDI）作为航运业的经济指标是航运市场的“晴雨表”，是衡量国际干散货海运市场运价的综合指标。根据船型的不同，BDI指数又可以分为波罗的海海岬型指数（BCI）、波罗的海巴拿马型指数（BPI）、波罗的海轻便型指数（BHMI），以上三个指数各占三分之一的权重。采购经理人指数（PMI）作为经济变化的“晴雨表”，可以有效的反映经济变化的趋势，具有一定的超前性，该指标是通过对采购经理的月度调查汇总出来的综合指数。中国采购经理人指数是由制造业PMI和非制造业PMI共同组成。制造业采购经理人指数的调查直接面向企业采购一线，通过多项指标的加权汇总，可以及时的把握市场脉搏，同时比较准确的反映企业状况。中国作为制造业大国，干散货海运在企业的生产制造中发挥着非常重要的作用，因此，波罗的海干散货运价指数与中国制造业也存在着紧密的联系。本文深入研究波罗的海干散货运价指数与中国制造业之间的关系，将有助于反映我国制造业发展水平以及规避干散货海运运价的波动风险。

1.相关研究文献评述

国际航运市场在世界贸易中占有重要地位，全球90%以上的贸易都是通过海运来完成，而干散货航运市场又是各细分航运市场中规模最大、发展也最成熟的航运市场。为了分析该指数的演变规律、研究市场的走势，学者们从不同的角度对该指标进行了研究，其中主要的研究思路就是研究波罗的海干散货航运指数变化与相关指标的关系。

陈丽芬等[1]利用SVAR 模型对干散货运价和燃油价格进行了相关性分析，结果表明，干散货运价与燃油价格的短期波动存在双向因果关系，但两者交互影响的显著性具有差异性干散货运价和燃油价格的短期波动具有双向因果关系，但两者交互影响的显著性有所区别，燃油价格的上涨对波罗的海干散货运价指数的增长存在显著影响。RUAN 等[2]运用MF-DCCA 分析了BDI 与原油价格间的相互关系，结果表明BDI 与原油价格的交叉相关系数具有显著的多重分形特征，在短期内交叉相关具有较强的持久性，而在长期内是弱持久的。姜宝等[3]运用DCC-GARCH、波动溢出指数模型测度国际干散货运价对我国钢铁股价波动的溢出效应以及传导机制，研究表明：干散货运价对国际铁矿石价格、中国钢铁股价的波动溢出效应均不显著。李瑞华等[4] 通过VEC模型研究了金融市场与航运市场间的关系，结果表明BDI 与黄金价格和道琼斯指数存在负相关的协整关系，可用来帮助判断BDI的走势。

关于PMI 指数的研究，国内外学者的研究方向大致为PMI指数本身的预测、借助PMI指数对GDP进行研究、以及PMI指数与其他变量间的关系。国内外文献大多集中在PMI 与商品市场中各个指数之间的相关性，如CPI、PPI、CCI 等。张宁等[5]利用双变量VAR 模型得到PMI 和PPI 的相关关系，即PMI 是PPI 的原因，可用于PPI 的波动趋势。宁波[6]在研究了CCI、CPI 和PMI三者的因果关系时则采用VEC 模型。杨书皓[7]的研究结果表明PMI 不能用于预测沪深300，而沪深300 有助于预测PMI。

根据现有研究，很少有学者将波罗的海干散货航运指标与中国制造业进行相关性研究。干散货航运运价与世界经济是息息相关的，全球经济发展迅速贸易量增加，则对航运市场干散货的运力需求也随之提高，运价指数相应上涨。中国作为世界制造业强国，全球进出口贸易大国，研究干散货运价市场与中国制造业之间的关系就显得非常重要。而直观体现两者的相关关系的方式就是对波罗的海干散货运价指数PMI和中国制造业PMI研究。为此，本文将分析BDI和中国制造业PMI 的数据，建立VAR 模型，进行Granger 因果检验、脉冲响应分析和方差分解，研究BDI和中国制造业PMI 之间的相关性。

2.实证分析

2.1样本选择

本文选择2005年1月至2020年4月的184个月度数据作为研究对象。其中制造业PMI数据来源于国家统计局，BDI的月度数据来源于克拉克森。为了减少异方差的影响，对制造业PMI和BDI的原数据进行自然对数变换，分别记为LnPMI和LnBDI。本文使用Eviews8软件进行实证分析。

2.2平稳性检验

本文通过ADF检验对序列的平稳性进行检验，可以发现LnBDI在5%的显著性水平下拒绝原假设，LnPMI在1%的显著性水平下拒绝原假设，两个序列都为平稳性时间序列，满足构建VAR模型的条件，检验结果如表1。

2.3建立VAR模型

在VAR模型建立之前要确定最优的滞后阶数p，但是滞后阶数的选择存在矛盾的特性。p越大，越能反映模型的动态关系;但p值又不能太大，p值过大，待估参数多，自由度降低严重，会直接影响模型参数估计的有效性。

因此，Eviews會提供多种标准来判断滞后阶数，本文综合LR、AIC、SC等五项指标确定最优滞后阶数。结果表明滞后两阶为最优，因此确立VAR（2） 模型。结果如下。

LnPMI=0.414676×LnPMI（-1）+0.136942×LnPMI（-2）+  0.072538×LnBDI（-1）-0.062640×LnBDI（-2）+1.694811

LnBDI=0.203742×LnPMI（-1）+ 0.218239×LnPMI（-2）+  1.231707×LnBDI（-1）-0.309766×LnBDI（-2）-1.092044

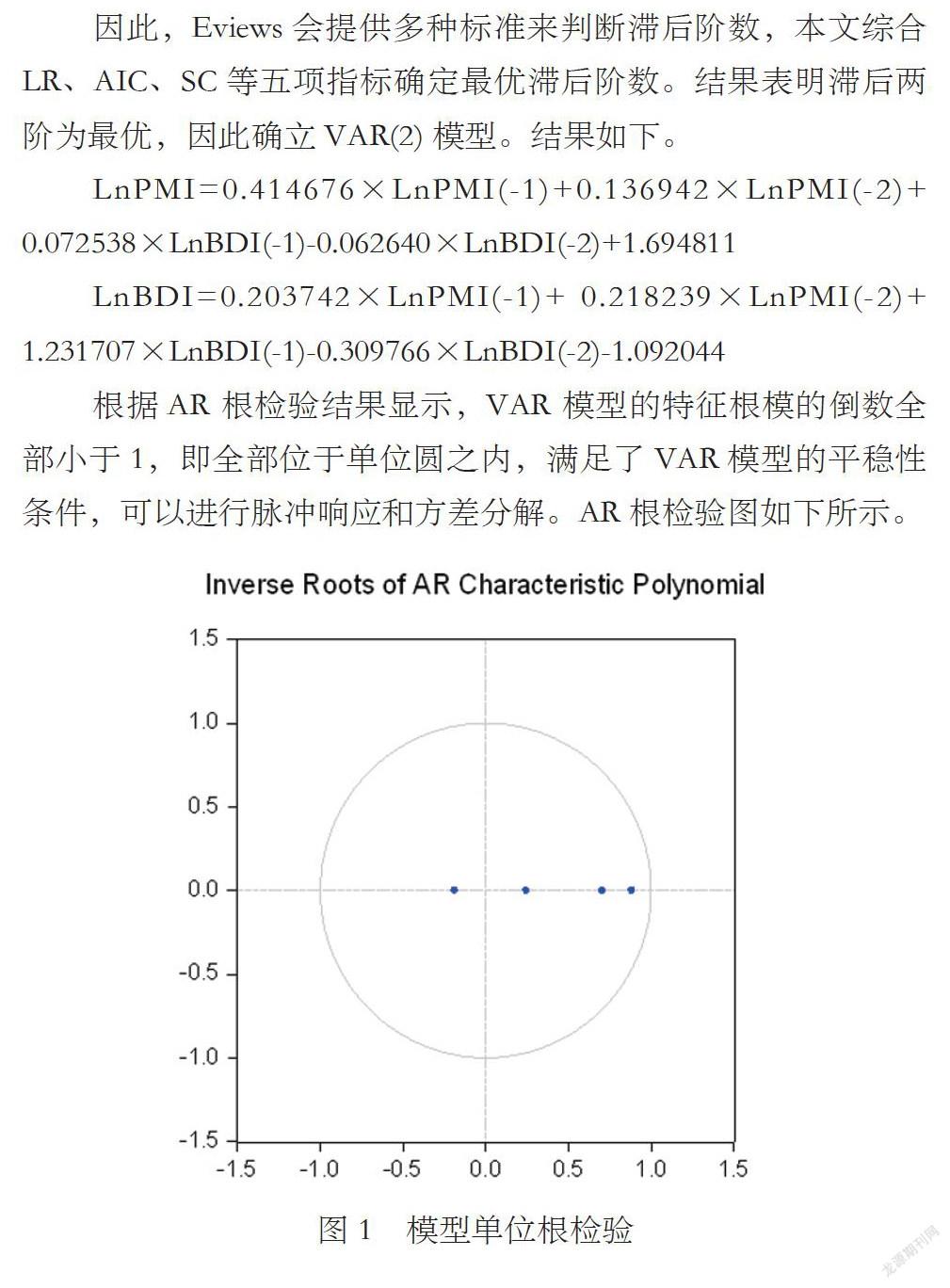
根据AR 根检验结果显示，VAR 模型的特征根模的倒数全部小于1，即全部位于单位圆之内，满足了VAR模型的平稳性条件，可以进行脉冲响应和方差分解。AR根检验图如下所示。

2.4Granger 因果检验

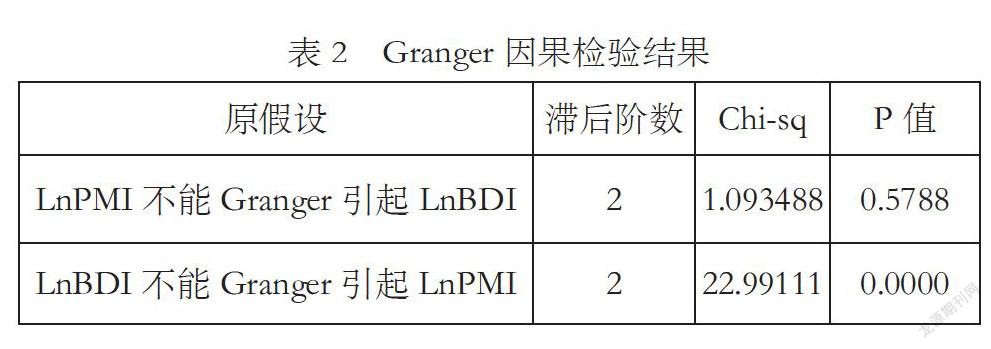
Granger 因果检验用于分析变量间是否存在短期因果关系，其原理是验证VAR 模型中某个变量是否受其他变量的滞后变量影响，若存在，即构成因果关系。由表可知，原假设“制造业PMI不是波罗的海运价指数（BDI）变动的Granger原因”在5%显著性水平下被接受，即制造业PMI对波罗的海干散货运价指数影响不显著，通过制造业PMI不能很好预测波罗的海运价指数。而原假设“波罗的海干散货运价指数不是制造业PMI变动的Granger原因”的P值小于0.05，在5%显著性水平下被拒绝，即波罗的海干散货运价指数对中国制造业有显著的影响，可以用于预测制造业PMI。

2.5脉冲响应分析

为了更好的分析LnBDI和LnPMI之间的关系，采用脉冲响应分析得到脉冲响应函数图如下。从图2左侧LnPMI对LnBDI冲击的响应图可以发现，给BDI一个正的冲击，对制造业PMI从第1期到第2期递增，在第2期达到峰值，随后开始缓慢减小并在第4期之后缓慢趋近于0，但影响一直是正向的。从下图右侧的LnBDI对LnPMI冲击的响应图可以发现，对于来自制造业PMI的冲击正向冲击，对BDI的影响开始为0，在0.5期开始缓慢上涨，并在第五期之后维持在相对稳定的状态，且BDI的反馈都是正向的，表明制造业PMI对BDI的影响时间相对较长。总之，脉冲响应分析表明制造业PMI 和BDI之间是相互影响的，都能产生正向的影响。

2.6方差分解分析

对制造业PMI和BDI分别做方差分解，结果如图3所示。

从方差分解图和分解表可以看出，波罗的海干散货运价指数对自身的冲击和影响最大，10 期之后对自身的解释力度仍然有98.34%，而制造业PMI在第二期开始有影响，第十期时也仅仅为1.66%。这与海运行业和该指数的特性有关，一方面，海运行业的垄断性质使得运价的指定并不仅仅考虑需求量的问题;另一方面，该指数是面向全球的运价指标，中国虽然是制造业大国，对干散货海运的需求也很大，但并不能起到决定性的作用。

而制造业PMI受BDI的影响就较大，贡献率在前4期增长迅速，随后缓慢稳定增长，在第10期达到了41.25%。这说明干散货海运运价对我国制造业的影响较为显著的，企业会将干散货海运运价作为产品生产制造计划调整的因素之一。

3.结语

本文选取2005年1月至2020年4月的中国制造业采购经理人指数（PMI）月度数据和波罗的海干散货运价指数（BDI）月度数据构建VAR模型，并通过格兰杰因果检验、脉冲响应分析和方差分解，可得如下结论：在短期内，中国制造业PMI和BDI的影响是单向的，中国制造业PMI的变化对BDI的影响并不显著，而BDI却是带动中国制造业PMI变动的格兰杰原因，且由方差分解可以看出该影响较为显著。

由以上结论，可得以下启示：我国应该加强对进出口贸易和航运企业信息的监测，及时准确的提供运价等相关信息，使得企业可以及时调整生产配置计划;同时应该积极发挥航运联盟的作用，避免因盲目的竞争而引起的市场剧烈波动，优化运力配置，合理调整运价。

参考文献：

[1]陈丽芬、谢新连、桑惠云、王文.基于SVAR模型的干散货运价和燃油价格的相关性分析[J].大连海事大学学报，2016（4）.

[2]RUAN Q S，WANG Y，LU X S，et al.Cross-correlationsbetween Baltic Dry Index and crude oil prices[J].Physica A： statistical meahanics and its applications，2016（7）：278-289.

[3]姜宝，张琪，李剑.国际干散货运价对我国钢铁股价波动溢出效应研究[J].价格理论与实践，2018（05）：99-102.

[4]李瑞华，宋炳良.基于协整理论的海运价格指数影响因素[J].中国航海，2014（3）：123-126.

[5]张宁， 陈晴旖.PMI 指数与我国物价水平相關性实证分析[J]. 商业时代，2013，15：34-35.

[6]宁波.CCI、CPI、PMI 的关系研究及实证分析[J]. 现代商贸工业，2018，17：101-102.

[7]杨书皓. 沪深300 指数与我国制造业PMI 关系的实证分析——基于VAR 模型[J]. 现代交际，2018，9：63-64.