最小二乘法在生猪价格与恩格尔系数关系中的应用

林宸

摘 要：2018年末以来，随着猪流感疫情的不断传播发展，国内的生猪价格飞涨，这对人民的生产生活造成了一定的影响。为此本文希望通过研究猪肉价格和居民生活相关的恩格尔系数之间的关系，探究生猪价格的变化对恩格尔系数的影响。本文根据最小二乘法，利用EXCEL对广州等五个城市的调研数据进行拟合分析，给出相关合理解释，并预测2019年的恩格尔系数。

关键词：最小二乘法;EXCEL;曲线拟合;预测;

1.引言

恩格尔系数是用于衡量一个国家或地区居民用于食品类支出占所有花费总比重的数字，由德国统计学家恩格尔于19世纪提出[1]，随后在不同国家和地区得到了广泛的应用。特别地，恩格尔系数在我国的统计数据中也占有举足轻重的地位，每年的统计数据也不可或缺。由于2018年以来全球各地爆发的猪瘟疫情蔓延到中国，使得我国的生猪行情收到很大影响，各地的猪肉价格也一路走高，猪肉相关概念股也随之飞涨。这激发本文去探究生猪价格对恩格尔系数的影响关系，并通过统计数学的相关方法，对此进行研究。

另一方面，在进行科学实验和工程实践的过程当中，经常遇到一些复杂的问题，这些问题最终都可以归纳为数学方程组。通过对这些数学方程组或者模型进行分析和求解，得到问题最终的解。但是并不是所有的模型都可以采用数学分析的方法。因此就产生了通过将这些连续的模型转换为离散的模型，通过差分方法得到最终解。这就是数值分析发展的过程，由此产生了一系列的数值计算的方法。本文研究的最小二乘法即是其中的一种方法，是一种使用较为广泛的数值优化方法，是18世纪勒让德和高斯共同发明发展用于统计及其误差推算，应用极为广泛的计算方法。这方法及其发展延伸的算法几乎应用于所有的统计计算中。包括同学们考试成绩推算，学区房价推算及猪肉价格分析，气温和冰镇可乐销售量的关系分析等等[2-4]。最小二乘法是找寻拟合函数值与实际函数值之差的平方和最小的方式，来构建该拟合函数，即所有观察点的误差的平方和最小。利用最小二乘法拟合出的曲线，还可以对其余的数据进行估计或预测。

本文通过观察不同城市的生猪价格和恩格尔系数的关系，利用最小二乘法的原理，对其关系进行量化，进行曲线拟合，并对2019年的恩格尔系数进行估计预测。

2.最小二乘法

2.1 最小二乘法的原理

假设随机变量Y与x存在某种相关关系。x是一般变量，而Y是随机变量，则对于每一个确定的x值，Y有其分布，并且对于每一组这样的（x，Y），都有潜在的对应关系。我们去考察其中的關系，求Y的数学期望，记为E（Y）。我们记E（Y）=μ（x），其中μ（x）为x的拟合函数。在实际问题中，拟合函数μ（x）一般是未知的，进行拟合分析的任务是在于根据实验数据去估计拟合函数，并且对所求出的拟合曲线进行分析，讨论其是否合理等内容。

对于x取一组不完全相同的值x1，x2…xn，设Y1，Y2，…Yn分别是其独立的观察结果，称（x1，Y1），（x2，Y2），…（xn，Yn）是一个样本集合，将其描绘在直接坐标系中，得到一系列散点，叫做散点图。通过散点图的形状，可以大致看出拟合函数μ（x）的表达形式。一般而言，μ（x）的表达形式可以是一元函数形式，也可以是多元函数形式，针对一元函数表达式，我们令表达式为μ（x）=a+bx，此时对μ（x）进行估计的问题就叫做一元线性拟合问题。假定对于所观测区间内的所有点（x，Y）都有，Y服从于a+bx，且误差的绝对值不超过σ2，记为

2.3曲线拟合

曲线拟合就是从给定的数据点当中找出这些数据点所呈现的规律，通常这些点的规律可以用曲线的函数方程进行表示。曲线拟合广泛应用于科学实验和工程实践当中，是拟合中的一种重要方法。曲线拟合适用于观测数据的误差较大，不可能也没有必要将它作为准确值来处理的数据问题，则只要求所构造的函数尽可能靠近这些采样点即可。即要求所构造的函数gx和采样点（xi，yi）（i=1，2，…n）之间满足某种误差准则，如满足最小二乘法的曲线拟合关系，

使总的偏差Q最小。按照上述要求构造函数gx的方法，就是曲线拟合方法。其中gx称为拟合函数。可见曲线拟合方法是用于观测数据本来就含有不可避免误差的场合，其中构造出的函数gx不需要都通过这些采样点（xi，yi），而只需要尽可能的靠近这些采样点即可。为了提高拟合函数的精度或准确性，我们应该增大观察的样本，提供数量足够多的采样点。

3.最小二乘法的应用

本文通过调研得到五个城市不同年份的猪肉价格和恩格尔系数，对其进行建模分析，利用最小二乘法进行曲线拟合，量化二者之间的关系。然后根据2019年的猪肉价格，对当年的恩格尔系数进行预测。

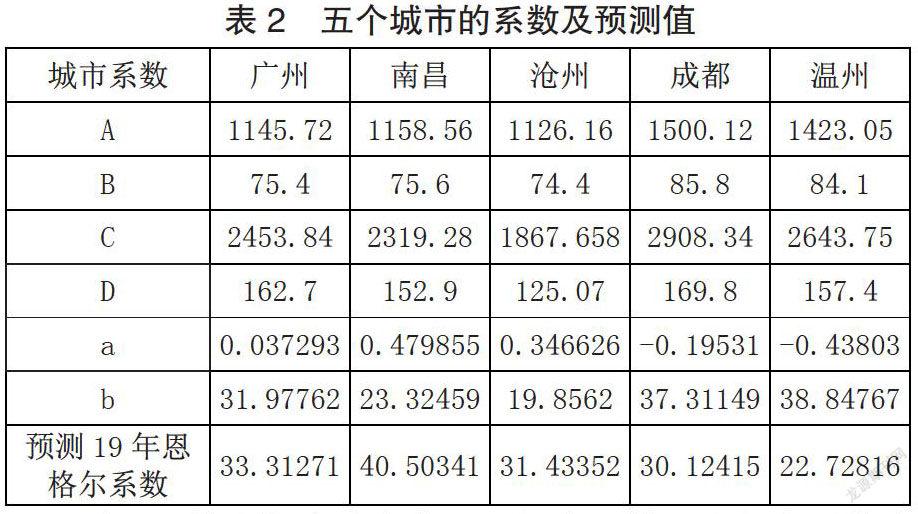
通过第二章的公式进行计算，得到每个城市对应的曲线的参数值结果如下表所示：

则可计算出每个城市的一元拟合函数，比如广州的为y1（x）=0.037293x+31.97762：，则带入2019年的猪肉价格35.8，可以得到2019年度的恩格尔系数33.31271。同理可得其他几个城市的拟合函数和2019年预测的恩格尔系数。

接下来我们将用EXCEL软件对这些数据进行处理，并且通过EXCEL图表的方式对拟合曲线与点的关系进行直观的展示。

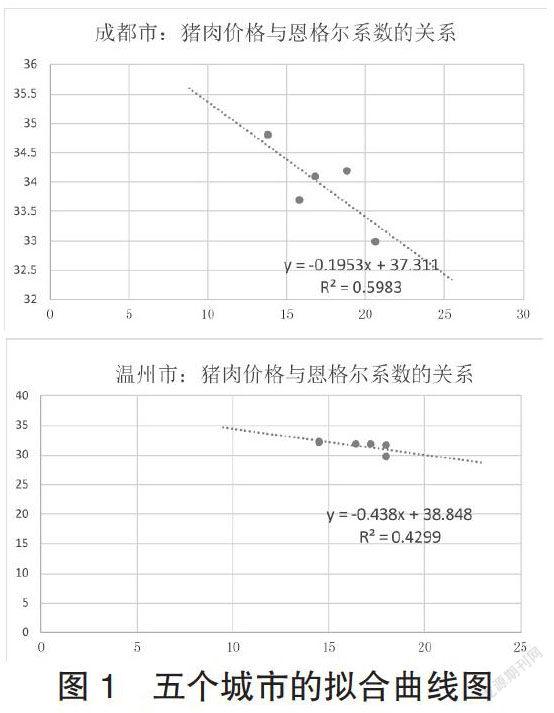
如图1所示是五个城市的猪肉价格和恩格尔系数的一元函数拟合曲线，从图中可以看出，各个点都分布在函数的周围，并且是以平方和最小的方式排布的。因此我们可以说猪肉价格对居民恩格尔系数有一定的相关性的影响。1）广州、南昌、沧州等三市恩格尔系数随着猪肉价格的上涨而升高，呈现正相关性。成都、温州两市恩格尔系数随着猪肉价格的上涨而下降，呈现负相关性。这可能是由于成都、温州两市本来就在肉类支出较高，因此猪肉价格上涨之后，适量的减少了采购，居民对猪肉价格的上涨有很大的调节空间。2）而为何广州猪肉价格和南昌猪肉价格相差不大情况下，广州的恩格尔系数会比南昌的要高，这主要是因为恩格尔系数的影响因子较多，猪肉价格仅是一方面原因，比如广州对饮食方面的支出较大，因此虽然广州的人均GDP较高，但还是猪肉价格差不多的情况下，出现了恩格尔系数较大的情况。

综上，恩格尔系数和不同城市的饮食文化，消费理念也有较大关系。经济数据只是客观反映实际情况，但是受多方面因素的影响。并且根据该拟合曲线，我们可以计算出2019年的恩格尔系数，对重要的经济数据指标预估。

4.结论

本文通过对最小二乘法原理的介绍，描述了其自变量与因变量的关系，以及怎样利用已知数据计算其一元拟合函数的相关系数。最后将最小二乘法应用到实际生活当中，通过调研不同城市猪肉价格和恩格尔系数，量化了二者之间的关系。并且利用EXCEL软件对这一关系进行了直观的展示，分析了其中的原因。最后对2019年为公布的恩格尔系数进行了预测，能对居民的生活质量和当前经济形势有一个前瞻性的了解。

参考文献

[1] 王少飞.用恩格尔系数衡量居民生活水平的可行性研究[J].统计研究，2002（6）：19-22.

[2] 邹乐强.最小二乘法原理及其简单应用[J].科技信息，2010（23）：282-283.

[3] 陆健.最小二乘法及其应用[J].中国西部科技，2007（12）：19-21.

[4] 商继敏，王海燕，蒋逢春等.最小二乘法对温度传感器测温数据线性拟合及其应用[J]，大学物理实验，2019（2）：81-84.