读懂儿童，让深度学习真发生

林超

摘要：小学数学的课堂教学是一个动态生成的过程，存在着许多不确定的因素。陶行知指出：“学生拿做来学，方是实学。”这里的“实学”与“深度学习”是高度契合的，需要教师在抓住课堂动态生成的同时，将教学中的生成顺势演变为推动教学发展的有利因素。

关键词：小学数学 深度学习 读懂学生

陶行知先生在撰写《教学做合一》一文时指出，教的方法要根据学的方法来定。后来他又进一步阐述，“事怎样做就怎样学，怎样学就怎样教；教的法子要根据学的法子，学的法子要根据做的法子” 。为了达成这样的目标，笔者在课前精心设计教学，努力做到充分预设，到了课上却发现学生提的问题太奇特，看似简单却又不是三言两语能说清的，若是停顿在此，进度就会大受影响；若是含糊应付，显然有悖于教育的目标。

“深度学习”，是学生在教师的引领下，围绕着具有挑战性的学习主题，积极参与、体验成功、获得发展的有意义的数学学习过程，这与“实学”不谋而合。现在学生的生活阅历本来就丰富，容易出现奇思妙想，课堂中会出现种种思维火花，教师要能在课堂上读懂学生思维困惑，把握课堂的即时学情，做出合理的教学决策。陶行知主张，“让孩子成为知识的发现者”，那只有读懂了课堂中学生的学习过程，才能与学生展开深度的互动，才能对预设是否符合学生的实际做出判断，并及时做出合理的教学决策。在这里，笔者结合自身的教学实践，认为可以从三个方面做到“读懂儿童”。

一、理解学生：读懂儿童思维的困惑

数学课堂如果没有思维的碰撞和心灵的交流，就无法充满生命力，最终会深陷“预设”的窠臼。只有经过课堂的洗礼，学生在学习过程中才会暴露出问题，这些问题在教师的眼中或许仅是一个个未经深思的“糊涂”答案，但若是能利用这些“糊涂”的出错方式，多付出一点时间，结合学生在解题时容易出现的错误，有意识地“误导”，看学生能否发现漏洞，就能以此培养学生分析和解决问题的能力。

例如，在教学《长方体和正方体的体积》一课时，有这样一道例题：棱长6分米的正方体，它的表面积和体积各是多少？学生很快便计算出了结果。此时，笔者稍一停顿，问道：“通过计算，你发现了什么？”这时，马上就有学生接话道：“得数都是216！”笔者立即顺着学生的答案接着说：“看来，这道题中的正方体的表面积和体积正好相等。”不出所料，一片赞同之声立刻此起彼伏地响起。不过，也有清醒的声音稍后响起：“老师，您的说法不对！”按照常规的套路，这时无非就是对两个答案所表示的意义进行辨析，然后很顺利地过渡到对面积和体积的再次认识上。而笔者在课前预设时认为，虽然常规的处理方法所需时间不多，也能达到预期的教学效果，但过于强调对数学概念的灌输与记忆，这样是把教学作为一个结果来进行，而不是作为一个过程来进行，学生很难真正理解所要学习的内容。因此，笔者决定在这个环节多花一点时间来突破。

听到不同的意见后，笔者心中窃喜，指着黑板上的两个答案，装作很惊讶地说：“这明明是相等的嘛！难道算错了？”此时，不同的见解纷纷冒出，于是笔者组织了一场小小的“辩论赛”。甲方认为这种说法是正确的，因为它们的算式都是6×6×6，结果也是相同的，都是216。而乙方反驳道：这个说法完全是错误的，虽然这两题的列式相同，可两个算式表示的意义完全不同，计算表面积的算式中最后一个6，表示的是面的个数，而计算体积的算式中的最后一个6，则表示的是棱长。所以，表面积用的单位是平方分米，而体积用的单位是立方分米。尽管算式相同，结果相同，可它们表示的是两种不同的概念，所以它们是不能比较的。这一方还举出一个相似的例子加以证明：在五下学习过地《圆的周长和面积》中，有这样一道判断题：半径是2厘米的圆的周长和面积相等。这题是错误的，理由和本题一样。

就这样，面对学生的困惑，笔者没有选择视而不见，而是慢下来，鼓励全班学生一起来直面困惑，展开思维碰撞。笔者鼓励学生纠错，一是引导持有不同观点的学生展开辩论，不管之前正确与否，学生的思维过程得到了充分的展现，正好借此了解学生是否真正理解了所学的知识，便于教师及时做出反馈评价，从而有针对性地进行纠错，使得教学相长；二是学生对本题有错误的理解其实并不意外，在产生不同见解时，不能让学生沉迷于“生成”的闭囿中，也切忌矫枉过正，把学生带进空中楼阁。通过这样的辩论，学生能对所学的表面积和体积的概念形成内化，从而对知识理解得更加透彻。陶行知也指出：不能引导人做之教育，是假教育。这样的辩论方是真做。

二、支持學习：引导儿童认知的进阶

现今的数学课堂是师生多向、开放和动态的对话、交流过程。故而在教学中，应该激活学生的思维，创设出师生、生生之间自然、和谐、智慧的对话氛围，通过他们的质疑、释疑，使得整个课堂变得充满活力，为生成插翅添翼。在这个过程中，师生、生生的对话或许不像语文学科那般，可以在富有韵味的语言世界里去体验五彩斑斓的生活，但也必须要让学生更独立、更充分、更深入地进行思维上的碰撞，让一个个鲜活的个体在主动的参与中，将思考的脉络清晰呈现于眼前。笔者认为，此时为了倾听每一个学生的对话，读懂每一个学生的发言，需要多付出一点时间上的等待。

例如，教学《用字母表示数》一课中，在学习了其中简单的数量关系之后的巩固阶段，我出示了一首比较复杂的“青蛙儿歌”：一只青蛙一张嘴，两只眼睛四条腿；两只青蛙两张嘴，四只青蛙八条腿……再让学生根据相应的数量关系继续往下编儿歌的同时，我还让学生用一句话来表示这首儿歌：（ ）只青蛙（ ）张嘴，（ ）只眼睛（ ）条腿。

按说有了数量关系，这句话就非常容易说了。果不其然，一个学生张口就道：“a只青蛙a张嘴，b只眼睛b条腿。”话音刚落，之前还跟着这个小伙伴一起摇头晃脑的学生立马就七嘴八舌了。我示意学生少安毋躁，将他的回答在心中迅速地过了一遍，接着问他：“我能理解你的想法，不过，青蛙的只数和腿的条数一样吗？”

这个学生迟疑地摇了摇头，虽没能马上改正，但却启发了他身旁的一个学生。第二个学生说道：“应该是a只青蛙a张嘴，b只眼睛c条腿。”虽然他发言完后，议论声一点没小，但我仍然表扬他“已经注意到在同一题中用不同的字母表示不同的量，真细心，希望所有同学都能畅所欲言”。得到了我的鼓励，学生的热情一下就高涨起来，第三个学生起身说道：“应该这么说就对了：a只青蛙a张嘴，b只眼睛2b条腿。”“你说得真棒，想到找关系了！”夸奖完，我接着追问：“那你为什么用2b来表示腿的条数呢？”“因为青蛙腿的条数是眼睛的2倍！”他兴奋地喊道。

“真好，你只用两个字母就表示出这首儿歌了。同学们，有没有办法只用一个字母就表示出这首儿歌呢？”笔者趁热打铁，抛出最后的问题。学生闻言纷纷投入思考中，不多时就有学生答道：“a只青蛙a张嘴，2a只眼睛4a條腿。”在追问了字母表示的意思后，我表扬他善于动脑筋。

每当回想起这个教学环节时，笔者也在反思：为什么学生能将四种方法留在黑板上，并且他们的想法会一次比一次高明呢？答案或许就是当时，笔者读懂了第一个孩子的发言，从而产生了下面一次次的对话。在对话中，要允许学生出错，教师要珍视学生的各种创造结果，这样才能逐步把学生的思维引向更深处。“极高明而道中庸”，从这个意义上说，教与学的平衡是对事物本质的重新认识和准确把握，着眼点在于学生的学，而学生独特的数学学习方式就潜藏在他们的出错中。在出错中，他们才能暴露自己独特的思维步骤，若是如常纠正孩学生的错漏，就如陶行知说的，“如果天天卖旧货，索然无味，要想教师生活不感到疲倦是很困难的”。

三、提升学力：呵护儿童思维的创造

在数学课堂上，活动形式的改进、活动材料的丰富，造就了越来越多具有发散性思维的学生。他们对一个问题的思考，往往会有突破教师已有经验的“新点子”，而教师则从没对这一“经验”的合理性及时反思过，以至于当“经验”以外的情况出现时，不能准确做出合理评判。当然，教师不能把已有的教学经验归零，更需要的是在已有知识经验的基础上，去审视“经验”以外的“新点子”是否存在合理性。那么，课堂中若遇到此种情况，应该怎么办呢？笔者认为，此刻或许应该停下来，让学生说说这样算的道理，感悟学生的思考方法，以期迅速做出对自己教学经验合理性的审视。

例如，《长方体和正方体体积的实际应用》一课中有这样一道练习题：如下图，有一堆土，甲处比乙处高50厘米，现在要把这堆土推平整，使甲处和乙处一样高，要从甲处取多少厘米厚的土填在乙处？

这道题可以算是考验学生思维的“试金石”。在布置练习任务之后，不多时，一个学生就激动地大声说道：“我用方程来解，很简单！”说话间，飞快地写下了解答过程。

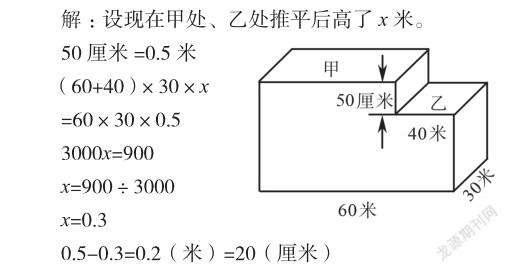
不出所料，这种方程解法由于容易理解，是最被学生所接受的解法，算是常规解法当中最深入人心的。此刻，笔者也巡视了教室一周，正待提问，这时有学生举手示意了：“我这儿还有一种算法！”“请你介绍一下。”刚刚巡视时，我就留意过他的做法，也是常规解法。“是这样的。”他接着说道，“因为两个土堆的底面都有一条棱长30米，所以可以将它们看作一个长是100米、宽是30米的不规则形体，此时这个不规则形体的底面积是3000平方米。原来甲比乙高出部分的体积是60×30×0.5=900（立方米），推平之后，甲、乙高度相等，就相当于将900立方米的土平均推在3000平方米的地面上。此时土堆会升高900÷3000=0.3（米），也就是30厘米，那么甲处就取了50-30=20（厘米）厚的土填在了乙处。”

这两种解法的相继出现，也意味着这道题的讲解接近尾声了。笔者正欲小结，这时一个学生又举手示意了：“我的方法和他有点不同。”“那请你来说说。”我按捺住好奇，和其他学生一起听她介绍。“可以先分别求出甲、乙两处的底面积，即40×30=1200（平方米），60×30=1800（平方米）。我发现甲处的底面积正好是乙处的1.5倍，而推平后，现在甲、乙的高度又相等，说明现在甲的体积也是乙的1.5倍。因此，整个土堆的体积可以看作2.5份。而原来超出部分的体积是900立方米，这样就可以求出现在乙需要推900÷2.5×1=360（立方米）的土，这就相当于甲处需要取360÷1800=0.2（米）=20（厘米）厚的土给乙。”

刚听完，笔者就觉得这个做法很新颖，还在回味之时，又有学生说道：“我的方法比她还简单。前面几步和她一样，后面没那么麻烦。就用50÷（1.5+1）=20（厘米）。”“怎么想的？”这时笔者的已有经验已经完全跟不上他的思路了。“通过前面的分析，我们已经知道甲的底面积是乙的1.5倍，现在甲、乙的高度又相等，所以现在甲、乙升高的高度应该是超出部分高度的1/2.5。”

陶行知认为，“学生具有惊人的创造潜力”，果不其然，在学生的文字表述、数式表述、模型表述中，这道题得到了升华。而这些形形色色的“个性”解法，散发着思维的芳香，彰显着个性的自由。课堂教学应该成为培养学生创新精神的广阔天地，教师要善于运用课堂教学的主渠道，时刻关注课堂中的动态生成，舍得花时间，将教学中的意外生成顺势演变为推动教学发展的有利因素。那么，为了这一时的闪光，多点等待又如何？

课堂上每个教学环节都要控制好时间，比如导入大概需要多少分钟，新授大概需要多少分钟，小组合作大概需要多少分钟……再好的教学设计，一旦超时就不完美了。但对于现在的学生，笔者却多了一丝操作时的弹性。在向40分钟要效益时，除了要高质高效地完成教学目标，同时还要培养学生的思维能力，提高学生的数学素养及独立解决问题的能力。在这个过程中，应合理利用课堂时间，优化课堂教学方式，从而激发课堂活力，提升教学效率，而这一切最终需要着眼于发展学生的核心素养。通过实践，教师加深了对数学学科本质的理解。若让“实学”真正得到落实，就让我们从读懂学生开始吧！

参考文献

[1]方明.陶行知全集[M].成都： 四川教育出版社，2009.

[2]中华人民共和国教育部.义务教育数学课程标准（2011版）[M].北京：北京师范大学出版社，2012.