剪切屈服型多耗能梁K形偏心支撑钢框架抗震性能研究
于海丰 吴杨周 马康 王焱
摘 要:为了解决偏心支撑钢框架结构延性导致的地震作用取值偏大等问题,研究了剪切型多耗能梁偏心支撑结构的抗震性能。在试验模型的基础上,基于耗能梁腹板受剪面积基本不变的前提下,把耗能梁段的截面设计成多耗能梁模式,采用ABAQUS有限元软件建立了8个数值模型,分别进行单调加载和循环加载,分析了破坏模式、滞回曲线、承载力、刚度及耗能能力随耗能梁个数变化的情况。结果表明,耗能梁段塑性变形发展充分,有效保护了其他的非耗能构件;结构的承载力、屈服位移及耗能能力要好于单耗能梁模型;每个多耗能梁模型的初始刚度相差较小(4%以内),均小于单耗能梁模型,但多耗能梁模型能够延缓结构刚度的退化速率。所提模型能提高结构的抗震性能,对实际工程应用有一定的参考价值。
关键词:结构设计;偏心支撑钢框架;剪切型耗能梁;腹板受剪面积;多耗能梁;抗震性能
中图分类号:TU391 文献标识码:A
文章编号:1008-1542(2020)04-0356-09
doi:10.7535/hbkd.2020yx04009
偏心支撑结构兼顾了中心支撑结构和纯框架结构的优点,具有承载力高、弹性刚度大、延性好以及耗能能力好等优点[1-3]。偏心支撑结构主要包括耗能梁、框架梁、柱以及支撑等4部分,在地震发生时主要通过耗能梁段的塑性变形耗散能量[4-6],而其他非耗能构件(框架梁柱、支撑等)基本处于弹性工作状态。由于具有较好的抗震性能,故中国建筑抗震设计规范[7](以下简称抗规)及JGJ 99—2015高层民用建筑钢结构技术规程[8](以下简称高钢规)规定,8度抗震设防区及以上宜采用偏心支撑钢框架结构。根据耗能梁长度的不同,规范[8-9]把耗能梁分为剪切屈服型、弯曲剪切屈服型及弯曲屈服型。比较而言,剪切型耗能梁的承载力高、抗侧刚度大、耗能能力好[10-12],因此目前的研究也多集中于带剪切型耗能梁的偏心支撑结构。如段留省等[13-14]、田小红等[15]研究了不同钢材组合下偏心支撑结构的抗震性能;殷占忠等[16-17]把耗能梁从框架梁中分离,使其作为一个独立的可替换构件,研究了耗能梁长度、加劲肋间距及焊接工艺孔对该结构体系抗震性能的影响。
目前,中国规范基于“小震弹性”计算地震作用,一方面,设计时不考虑结构体系的延性差异,即无法考虑偏心支撑钢框架结构延性带来的设计地震作用折减问题,导致结构地震作用取值偏大;另一方面,基于能力设计时,需要增加非耗能构件的截面尺寸以保证耗能梁段为唯一发生塑性变形的构件,故造成了偏心支撑结构用钢量的增加,经济性不佳。为此,吴清怡[18]、PRINZ等[19]基于减小腹板受剪面积的原理,对剪切型耗能梁段的腹板进行开洞削弱,以减小非耗能构件的设计截面,提高其经济效益(减小用钢量)。但规范[8-9]认为耗能梁腹板上开孔会影响其弹塑性变形能力,因此不建议对腹板进行开孔。基于此,本文提出了一种多梁形式的耗能梁(采用变相开孔方法,以减小耗能梁腹板受剪面积)。为详细考察所提出的多耗能梁偏心支撑结构的抗震性能,建立了8个有限元模型,分别对其进行了单调加载和循环加载分析,研究承载力、刚度及耗能能力随耗能梁个数的变化规律。
1 数值模拟有效性验证
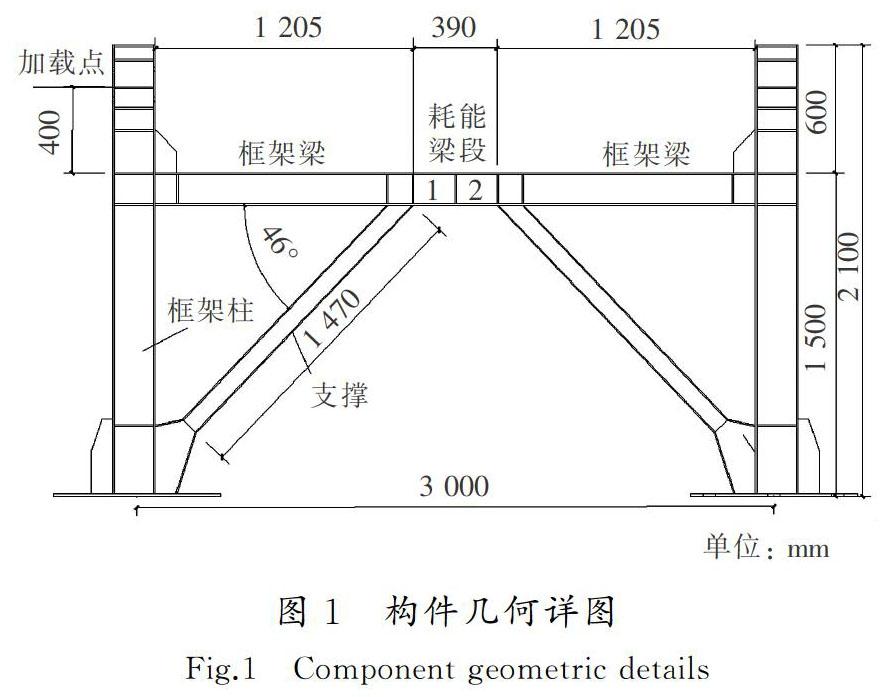
为验证数值分析的有效性,采用ABAQUS软件对某一单层、单跨、单榀偏心支撑钢框架结构的滞回性能进行了模拟。试验模型高1 500 mm,跨度3 000 mm,框架梁、耗能梁段截面为H150×130×6×8,框架柱截面为H200×130×6×8,支撑截面为H90×90×6×6,框架梁与框架柱之间、支撑与框架梁之间、支撑与框架柱之间均采用全熔透焊接连接,构件几何详图见图1。构件均采用Q235B级钢,材性试验结果见表1。水平荷载由1 000 kN液压作动器施加,规定推方向为负,拉方向为正。试验时,采用荷载-位移混合控制法,屈服前按50 kN递增,屈服后按nΔy递增,每级均循环2次,直至试验模型破坏,其中Δy为屈服位移,即荷载位移曲线出现转折时(结构屈服)所对应的位移。
采用壳单元S4R建模,钢材采用Von Mises多线性随动强化的三折线模型,考虑Bauschinger效应,力学性能见表1。网格划分时,为保证计算效率和计算的精度,只对耗能梁处和支撑处的网格进行细化,尺寸约为20 mm,框架梁的网格尺寸为20~150 mm,框架柱的网格尺寸约为50 mm,网格划分见图2 a)。为模拟试验中柱脚的约束条件,在模型中的柱脚位置设置2个参考点RP1和RP2,分别将2个垫板与2个参考点耦合并约束其6个自由度,实现理想固端;耗能梁段的侧向约束通过令Ux=0来实现。为模拟支撑可能出现的面外屈曲,在支撑跨中施加l/500的面外变形作为初始缺陷,l为支撑长度。加载时将荷载/位移同时施加在加载点(RP5和RP6),加载效果与试验完全相同,且建模简便,模型的边界条件详见图2 b)。
图3和表2给出了试验结果和数值分析结果。可见,有限元分析的耗能梁段和结构整体的变形总体上与试验的基本一致,由于有限元未考虑构件的初始缺陷,不会产生疲劳断裂等问题,故有限元模型中未出现支撑与框架梁焊缝连接处断裂等问题,而试验中出现了此现象(见图3 b))。有限元的滯回曲线和骨架曲线与试验的基本吻合,且有限元滞回曲线较试验的稳定;对于承载力来说, 有限元推拉各方向的承载力均低
于试验的,且屈服荷载Py和峰值荷载Pm亦低于试验的(见表2)。造成上述现象的主要原因在于:1)有限元分析时未能充分考虑材料硬化现象;2)试验模型中各种阻尼作用的存在;3)液压作动器进出油时不稳定。总体上,数值模拟结果与试验结果吻合程度较好,这表明可以采用数值方法开展偏心支撑钢框架结构的抗震性能研究。
2 多耗能梁模型抗震性能研究
2.1 多耗能梁有限元模型建立
本文在试验模型的基础上对耗能梁段截面进行改进,即在保证耗能梁腹板受剪面积不变的前提下,研究多组不同个数耗能梁组合的偏心支撑结构,耗能梁个数、腹板受剪面积与耗能梁截面尺寸见表3。除耗能梁段截面及长度(试验模型耗能梁长390 mm,多耗能梁长350 mm)不同之外,其他构件的截面尺寸及几何长度同试验模型完全相同。耗能梁段与框架梁通过端板连接,经过试算分析端板厚度取20 mm,耗能梁截面示意图见图4。
按照前述建模方法,建立了8个有限元模型,分别进行单调加载分析和循环加载分析。有限元模型中未考虑构件的初始缺陷,当耗能梁段的Mises应力超过材料的极限应力或模型发生较严重的屈曲、失稳而导致计算不收敛或结构的层间位移角超过1/25等作为有限元模型的破坏准则[20]。为消除不同加载制度对结构耗能的影响,循环加载统一采用位移控制法进行加载,初始位移值和每级位移增量均为8 mm,加载至88 mm(层间位移角1/17)停止分析;单调加载时位移加载至150 mm(层间位移角1/10)停止分析。
2.2 应力云图
分析结束时,单调加载各模型耗能梁段的变形(剪切变形)和结构整体变形(支撑面外失稳)基本相同,因此本文未给出单调加载时耗能梁段和结构整体变形的应力云图。图5为循环加载时的应力云图。由图5可知,各模型的变形主要集中在耗能梁段上(整体上为剪切变形,但耗能梁端部均出现了局部屈曲现象),其他非耗能构件基本处于弹性状态,当加载位移较大时,除L1模型、L2-1模型和L2-2模型外,其余各组模型支撑均出现了失稳现象,且各模型柱脚区域、支撑与框架柱连接区域略有塑性发展。各模型的端板均处于弹性状态,未发生变形。
2.3 单调加载结果分析
图6为各模型单调加载的荷载位移曲线,图7为荷载(屈服荷载Py、峰值荷载Pm、极限荷载Pu)、位移(屈服位移Δy(按“通用屈服弯矩法[21]”确定)、峰值位移Δm、极限位移Δu(承载力下降85%所对应的位移值))变化图,图7中虚线为L1模型值,表4为各模型的特征点响应。由图6可知,各曲线整体趋势相似,有较明显的直线段、较长的弹塑性段,构件屈服后荷载上升幅度较大,表明结构具有较高的安全储备。由图7 a)和表4可知,Py随着耗能梁个数的增加而增加,L1模型Py为372 kN,L6模型Py为408 kN,提升约9.7%,其他各组模型Py介于两者之间;L1模型(552 kN)和L2-2模型(553 kN)Pm相近,其他各模型的Pm均大于前两者,L3-a模型Pm最大为583 kN;Pu和Pm变化趋势相同,除L2-2模型Pu和Pm略低于L1模型外,其余各组多耗能梁模型的Pu均高于L1模型。由图7 b)和表4可知,随着耗能梁个数的增加,Δy整体趋势是先增大后减小,但多耗能梁Δy均大于单耗能梁L1模型的(Δy为10.5 mm),L3-a模型Δy最大为16.1 mm;Δu和Δm变化趋势相同,先增加后减小,L3-b模型Δu和Δm均达到最大,而L5模型和L6模型要低于L1模型;各模型均具有较好的延性且上位移角θ均满足抗规[7]1/50的要求。
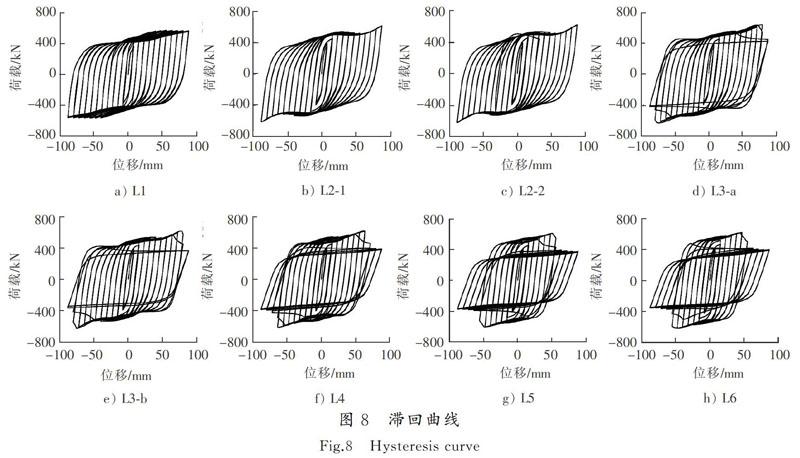
2.4 滞回曲线
循环加载下各模型的荷载-位移曲线见图8,各模型滞回曲线均为梭形,滞回环稳定且饱满,均表现出良好的耗能能力。由图8可知,L1模型、L2-1模型和L2-2模型在加载过程中滞回曲线未出现明显下降,L3-a模型和L3-b模型当加载至72 mm(对应层间位移角1/20.8)、L4模型当加载至64 mm(对应层间位移角1/23.4)、L5模型和L6模型当加载至56 mm(对应层间位移角1/26.7)时由于支撑出现失稳,故导致承载力出现了下降。
对于单调加载分析和循环加载分析来说,当支撑出现失稳时,模型的承载力均达到最大值,之后随着加载位移的增加承载力出现了明显下降,见图6和图8(L1模型、L2-1模型和L2-2模型的承载力未出现明显下降),总体上循环加载分析时各模型支撑出现失稳时的位移值与单调加载分析时的相差不大,且在支撑失稳前,多耗能梁模式的承载力和滞回曲线包络面积均要大于单耗能梁的,表明多耗能梁模式有利于结构的抗震性能。
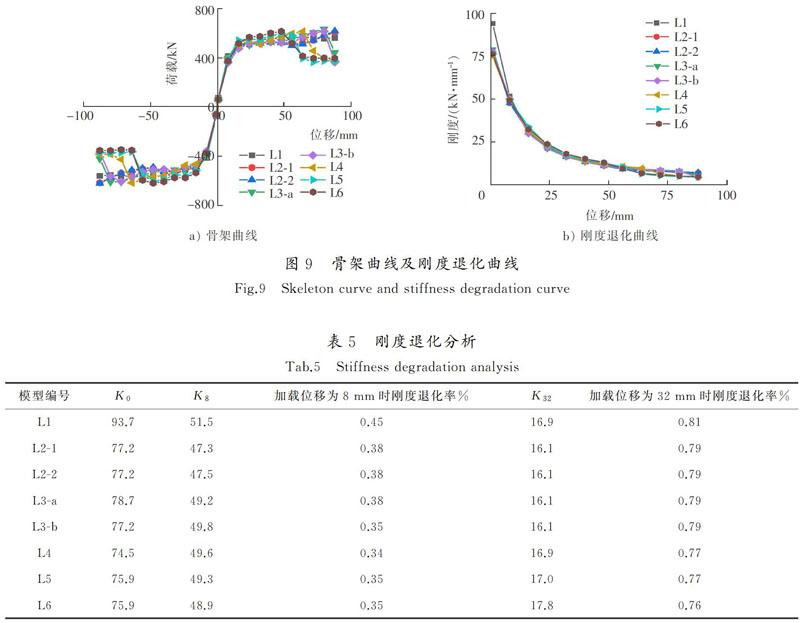
2.5 骨架曲线及刚度退化曲线
图9 a)为各模型的骨架曲线,图9 b)为刚度退化曲线,表5为刚度退化分析,其中K0表示结构的初始刚度,K8表示加载位移为8 mm时结构刚度,K32表示加载位移为32 mm(层间侧移角1/46)时结构刚度。由图9 a)可知,骨架曲线存在明显的线弹性段和弹塑性段,在线弹性段各模型骨架曲线重合。加载位移在56 mm之前(各个模型的支撑均未发生失稳现象)在相同的位移下L6模型和L5模型的承载力较大,L4模型次之,其余各组模型的承载力相差较小,均小于前两者;随着加载位移的继续变大,除L1模型、L2-1模型和L2-2模型外,其余各模型由于支撑出现失稳而导致承载力出现了明显下降。由图9 b)和表5可知, L1模型的K0较大,其余各模型K0相差较小(在4%以内),均小于L1模型的,各模型刚度退化趋势相同;当加载位移至8 mm时,L1模型的刚度退化率最大为45%,其余模型刚度退化率在34%~38%;位移加载至32 mm时,L1模型的刚度退化率最大为81%,其余各组模型的退化率在76%~79%。综上,单耗能梁K0较大但是刚度退化速率较快,多耗能梁的K0略小却可以有效延缓刚度退化的速率。
2.6 耗能能力
本文采用耗散总能量和等效粘滞阻尼系数来评价结构的耗能能力[21],见图10和表6。从结构耗散的总能量来看,L2-1模型、L2-2模型、L3-a模型、L3-b模型的总能量较L1模型分别增加3.95%,2.68%,5.69%和0.2%;L4模型、L5模型、L6模型耗散的總能量较L1模型分别减少1.21%,2.81%和13.67%。从等效粘滞阻尼系数he来看,当加载位移为Δy时,由于多耗能梁模型的屈服位移较大,各模型处于弹性状态,耗散能量较少,故he要小于L1模型;加载位移在2Δy~3Δy时,多耗能梁模型的he基本上和L1模型相差不大;而当加载位移增至4Δy~11Δy时,整体上多耗能梁模型的he要大于L1模型,但由于加载后期L5模型、L6模型支撑的面外失稳对结构耗能能力影响较大,故he要明显小于L1模型。综上,多耗能梁模型在加载前期耗能能力并未得到充分提升,但在加载后期其耗能能力表现较好,总体上要好于单耗能梁L1模型。
3 结 论
本文在试验模型的基础上对耗能梁截面进行了改进,通过ABAQUS建立了8个多耗能梁有限元模型,并对之进行了单调加载和循环加载分析,在本文分析的范围内可以得到如下结论。
1)数值模拟结果与试验结果吻合程度较好,表明可以采用数值分析的方法对偏心支撑结构进行抗震性能研究。
2)多耗能梁偏心支撑结构能够提高结构的承载力、屈服位移以及耗能能力,而结构的初始刚度要明显小于单耗能梁模型,各多耗能梁模型的初始刚度相差不大,但多耗能梁模型能够延缓结构的刚度退化速率。
3)L2-1和L2-2,L3-a和L3-b两组模型的初始刚度、屈服荷载、耗能能力等相差较小,且滞回曲线的饱满程度也基本一致,表明不同的布置形式对两耗能梁模型及三耗能梁模型的抗震性能影响较小。
4)结合对结构承载力、刚度、耗能能力等因素的分析,建议多耗能梁个数为2—4个,此时结构的抗震性能最佳。
总体上,本文所提出的剪切型多耗能梁模型能够提高结构的抗震性能,建议实际工程中加以采用。
本文只分析了不同的耗能梁个数对结构抗震性能的影响,今后可在多耗能梁模式的基础上针对耗能梁在端板上具体的布置位置及端板厚度等方面进行研究。
参考文献/References:
[1] SINA K A,CEM T.A review of research on steel eccentrically braced frames[J].Journal of Constructional Steel Research,2017, 128:53-73.
[2] HJELMSTAND K D,POPOV E P,Characteristics of eccentrically braced frames[J].Journal of the Structural Engineering,1982,110(2):340-353.
[3] 齐永胜,赵风华,李卫青.K形、V形偏心支撑钢框架抗震性能对比研究[J].结构工程师,2015,31(5):89-95.
QI Yongsheng,ZHAO Fenghua,LI Weiqing.Comparative study on seismic performance of K-shaped and V-shaped eccentrically braced steel frames[J].Structure Engineers,2015,31(5):89-95.
[4] BOSCO M, ROSSI P P. Seismic behaviour of eccentrically braced frames[J]. Engineering Structures,2009,31:664-674.
[5] 连鸣,李浩翔,莫文茹,等.可更换剪切型耗能梁段-高强钢框筒结构滞回性能数值分析[J].建筑结构,2020,50(1):83-90.
LIAN Ming, LI Haoxiang, MO Wenru, et al. Numerical analysis of hysteretic performance of replaceable shear link section-high strength steel frame tube structure[J]. Building Structure, 2020,50(1): 83-90.
[6] 孙山川,王新武,孙海粟,等.不同长度耗能梁段偏心支撑框架受力性能[J].河南科技大学学报(自然科学版),2020,41(1):56-61.
SUN Shanchuan, WANG Xinwu, SUN Haisu, et al. Mechanical properties of eccentrically braced frames with different lengths of energy dissipation beams[J]. Journal of Henan University of Science and Technology (Natural Science Edition), 2020,41(1):56-61.
[7] GB 50011—2010, 建筑抗震設计规范[S].
[8] JGJ 99—2015, 高层民用建筑钢结构技术规程[S].
[9] ANSI/AISC 341-16, Seismic Provisions for Structural Steel Buildings[S].
[10]张光伟,孟宏睿.K形偏心支撑钢框架耗能段长度对其抗震性能的影响[J].兰州理工大学学报,2018,44(4):137-141.
ZHANG Guangwei, MENG Hongrui.Influence of energy dissipation section length of steel frame with K-shaped eccentric brace on its anti-seismic performance[J]. Journal of Lanzhou University of Technology, 2018, 44(4): 137-141.
[11] ENGELHARDT M D, POPOV E P. Experimental performance of long link in eccentrically braced frames[J].Journal of Structural Engineering, 1992,118(11): 3067-3088.
[12]GHOBARAH A, RAMADAN T. Seismic analysis of links of various lengths in eccentrically braced frames[J].Canadian Journal of Civil Engineering,1991,18(1):140-148.
[13]段留省,苏明周.高强钢组合K形偏心支撑钢框架震后修复试验研究[J].地震工程与工程振动,2015,35(4):198-205.
DUAN Liuxing,SU Mingzhou.Experimental study on seismic retrofit of high strength steel composite K-type eccentrically braced frames[J].Earthquake Engineering and Engineering Vibration,2015,35(4):198-205.
[14]段留省,苏明周,郝麒麟,等.高强钢组合K形偏心支撑钢框架抗震性能试验研究[J].建筑结构学报,2014,35(7):18-25.
DUAN Liuxing, SU Mingzhou, HAO Qilin,et al. Experimental study on seismic performance of high-strength steel composite K-eccentrically braced steel frame [J]. Journal of Building Structures, 2014,35(7):18-25.
[15]田小红,苏明周,连鸣,等.高强钢组合K形偏心支撑框架结构振动台试验研究[J].土木工程学报,2016,49(3):56-63.
TIAN Xiaohong, SU Mingzhou, LIAN Ming,et al.Shaking table test study of high-strength steel composite K-eccentrically braced frame structure [J]. Journal of Civil Engineering, 2016, 49(3): 56-63.
[16]殷占忠,李锦铭,董龙光,等.偏心支撑钢框架可替换剪切连接件试验研究[J].建筑结构学报,2019,40(9):157-165.
YIN Zhanzhong,LI Jinming,DONG Longguang,et al.Experimental research on replaceable shear connectors of eccentrically braced steel frame [J]. Journal of Building Structures, 2019, 40(9): 157-165.
[17]殷占忠,王立功,张晓博.端板连接剪切型可替换独立耗能梁段的恢复力特性[J].兰州大学学报(自然科学版),2018,54(3):376-381.
YIN Zhanzhong, WANG Ligong, ZHANGg Xiaobo. The restoring force characteristics of the end-plate connection shear type replaceable independent link [J]. Journal of Lanzhou University (Natural Science Edition), 2018,
54(3): 376-381.
[18]吴清怡. 长圆孔腹板耗能梁段滞回性能研究[D].苏州:苏州科技大学,2018.
WU Qingyi. Research on Hysteretic Performance of Energy-Dissipating Beam Section with Long Circular Hole Webs[D]. Suzhou:Suzhou University of Science and Technology, 2018.
[19]PRINZ G S, RICHARD P.Eccentrically braced frame links with reduced web sections[J].Journal of Constructional Steel Research,2009,65(10):1971-1978.
[20]段留省,蘇明周.高强钢组合K形偏心支撑钢框架抗震性能分析[J].西安建筑科技大学学报(自然科学版),2015,47(1):46-50.
DUAN Liuxing, SU Mingzhou.Seismic behavior analysis of high strength steel composite K-type eccentrically braced frame[J]. Journal of Xian University of Architecture and Technology (Natural Science Edition), 2015, 47(1): 46-50.
[21]傅恒菁.建筑结构试验[M].北京:冶金工业出版社,1992.

