一种新型直流微电网DC-APF控制策略
高晓芝 乔宇 孙会琴 孙鹤旭 王磊 田晋
摘 要:针对直流母线电压存在的纹波分量会对整个直流微电网供电电能质量以及设备运行安全性造成影响的情况,提出了一种新型直流有源滤波器(DC active power filter,DC-APF)控制策略,抑制直流母线电压纹波。在分析DC-APF的多种模态工作基础上,对纹波检测和抑制方案进行了设计优化;提出了基于小波变换Mallat算法的直流母线电压纹波检测法;在传统PI与模糊PI控制的基础上,提出了改进的模糊自适应PI控制,实现对补偿电流的跟踪控制方法;在MATLAB/Simulink仿真环境中搭建了含DC-APF的直流微电网系统模型。仿真结果表明,与传统的DC-APF控制策略相比,新型DC-APF控制方法可以实现对直流母线电压纹波的快速检测,具有良好的纹波补偿抑制效果。所提策略可提升DC-APF对纹波的检测性能和抑制效果,为直流微电网纹波检测与抑制提供新的思路。
关键词:电力系统及其自动化;直流微电网;直流母线电压纹波;直流有源滤波器;小波变换Mallat算法;改进的模糊自适应PI控制
中图分类号:TM72 文献标识码:A
文章编号:1008-1542(2020)04-0303-12
doi:10.7535/hbkd.2020yx04003
与交流微电网相比,直流微电网中不存在无功功率的波动,也没有频率和相位同步的问题[1],因此直流母线电压成为衡量直流母线稳定的标准。直流微电网中直流母线电压纹波产生的主要原因如下:1)直流微电网通过双向 DC-AC 变流器连接到交流大电网,当交流电网中存在电网电压不对称的情况,以及存在谐波时,都会导致直流母线电压产生纹波分量;2)当交流负载通过 AC-DC变换器接入直流微电网,通过母线的电流不完全是直流,因为交流负载吸收的功率存在 2 倍于输出电压基波频率的脉动,这就会导致逆变器的输入电流存在二次纹波电流[2]。纹波的存在会使电压和电流波形发生畸变,影响微网中分布式电源和用电设备的工作效率,并对系统的安全运行造成严重危害。此外,纹波的存在也会使供电网络受到污染,严重影响微电网的电能质量。解决该问题的主要方法是加装滤波装置[3-4],通常采用无源滤波器和有源滤波器来抑制纹波。文献[5—6]分析了有源滤波器的优点以及研究现状,与无源滤波器相比,有源滤波器具有良好的动态性能。
现阶段对直流母线电压纹波分量的检测方法,主要通过低通滤波器提取出直流母线电压的纹波分量。但低通滤波器在选择截止频率时,难以同时兼顾检测精度和响应速度两项指标[7-8]。文献[9—10]中采用低通滤波器来提取纹波分量,但未对低通滤波器在准确性和响应速度方面存在矛盾的问题进行深入研究分析。文献[11]总结了几种常见的直流有源滤波器的拓扑结构,并对其工作模态进行了简要分析,但没有分析和研究DC-APF拓扑结构的可靠性以及拓扑结构所适用的控制算法。文献[12]中DC-APF采用双向全桥DC-DC变换器作为其主电路结构,其特点是可以稳定DC-APF直流侧电容电压,还可以将直流输出的纹波能量回馈到电网中,可有效降低系统的能量损耗,但主电路结构较为复杂。文献[13]对H桥级联型交流有源滤波器直流侧电容电压的稳定问题进行了研究,提出了直流侧电压三级平衡控制方法,从总体、相间、相内三级来解决其直流侧电压的不平衡问题,实现了直流侧电容电压的均衡稳定,可为直流有源滤波器的直流侧电容电压的均衡控制提供参考。
目前DC-APF对补偿电流的跟踪控制主要以PI控制方法为主,很多学者在此基础之上进行了改进。文献[14—15]采用传统的PI控制实现对补偿电流跟踪控制,其中,文献[15]采用阻抗分析法,通過建立小信号模型求解系统的闭环输出阻抗,确定PI控制器的参数,但该方法复杂,对于难以求解数学模型的复杂系统来说,缺乏实用性。文献[16]中在传统PI控制的基础上,引入重复控制的思想,虽能有效抑制稳态误差,但重复控制的动态响应速度比较慢,不能及时对纹波进行补偿。文献[17]提出了基于系统辨识的重复控制方法来实现DC-APF对补偿电流的跟踪控制,结合系统辨识和重复控制的优点,可有效提高系统的控制性能,但其适用环境为高压直流输电系统,是否适用于直流微电网环境,还有待进一步研究。文献[18]中在传统PI控制的基础上,引入无差拍控制和重复控制,提高了系统阻尼,增加了稳态精度,其缺点是无法根据系统状态的变化对控制器参数进行实时调整。文献[19]将传统的滑模控制和递归神经网络方法结合,提高系统的控制精度和鲁棒性,但控制方法较复杂,此外,其采用低通滤波器提取纹波分量,存在延迟性问题,会影响系统对纹波的抑制效果。
本文针对直流微电网中直流母线电压存在的纹波问题,给出了一种新型的DC-APF控制策略来抑制直流母线电压纹波:采用基于小波变换Mallat算法的直流母线电压纹波检测法,实现直流母线电压纹波的快速检测;采用改进的模糊自适应PI控制,实现对补偿电流的快速响应跟踪控制。
1 系统结构研究
1.1 直流微电网系统结构
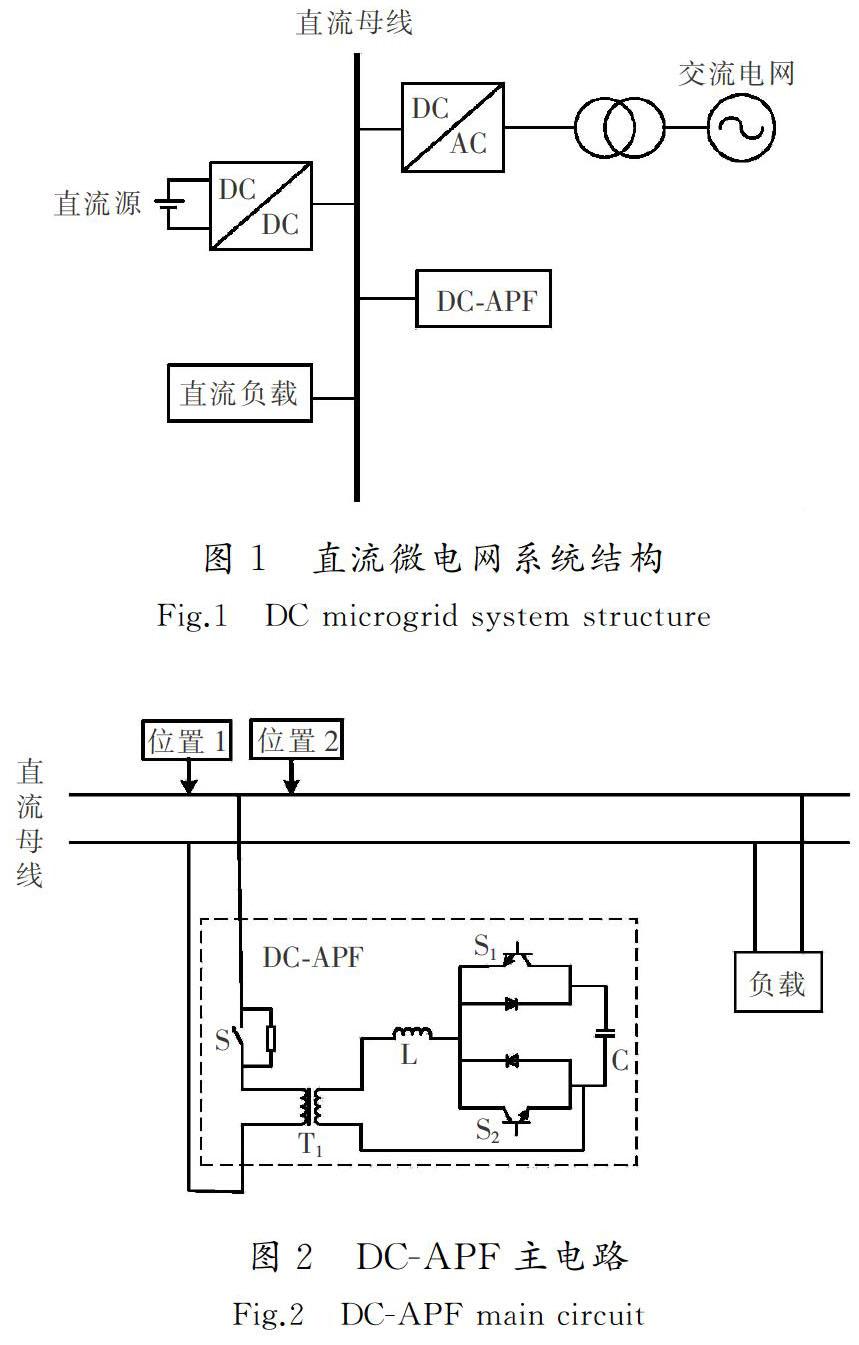
含DC-APF的直流微电网结构如图1所示,包含:1) 双向DC-AC变换器,用来连接直流微电网和交流电网,运行于直流侧电压控制模式,支撑直流母线电压;2)直流电压源,通过DC-DC变换器接入直流母线,以此来模拟分布式电源;3)直流电阻,用来模拟直流负载;4)DC-APF。由于本文主要研究DC-APF对直流母线电压纹波的抑制效果,参考文献[20]中的纹波产生方法,系统纹波主要通过设置交流电网电压三相不对称从而使直流母线电压产生二倍频纹波分量实现。
1.2 DC-APF的拓扑结构
图2为DC-APF主电路图,DC-APF接在直流负载侧。T1为隔离变压器;S为DC-APF启动开关;S1,S2为开关管,使用的是MOS管;L为滤波电感;C为直流侧电容。在位置1处,对未接入DC-APF时的纹波电流进行检测,在位置2处,对DC-APF工作后的纹波电流进行检测。DC-APF主电路采用了Boost-Buck(升降压)电路。DC-APF通过小波变换Mallat算法检测直流母线电压纹波,控制主电路产生补偿电流,该补偿电流与电流纹波相位相反、大小相等,以此来抵消直流母线上的电流纹波,从而对直流母线上的纹波起到抑制作用。如图3所示,Vdc为直流母线电压,VC为DC-APF直流侧的电容电压,ip为DC-APF产生的补偿电流。按照功率开关管的导通状态,在一个工作周期内分成了 4 种工作模态。
Boost工作模态1:如图3 a)所示,当主电路产生的补偿电流ip为正且小于微网中的纹波电流时,开关管S2导通,二极管D1,D2保持关断,流过电感L的电流iL正向增加,则有:
Buck工作模态4:如图3 d)所示,当主电路产生的补偿电流ip为负且大于微网中的纹波电流时,关闭开关管S1,电感电流通过二极管D2续流,开关管S2和二极管D1保持关断,电感电流iL反向减小,则有:
通过对DC-APF拓扑的工作模态分析,可以看出,当补偿电流ip>0时,DC-APF工作在Boost状态;当补偿电流ip<0时,DC-APF工作在Buck状态。根据检测到的直流母线电压纹波,控制主电路产生与纹波分量幅值相等、方向相反的补偿电流,注入到直流微电网中,以此来抑制直流母线电压中的纹波分量。
2 DC-APF的控制策略
本文所采用的DC-APF的整体控制策略如图4所示,主要分为直流母线电压纹波检测、DC-APF直流侧补偿电容电压控制、DC-APF的补偿电流跟踪控制策略3部分。
1)直流母线电压纹波检测。采用基于小波变换Mallat算法提取出直流母线电压udc中的直流分量ud,ud与udc相减,得到直流母线电压纹波分量uref,uref乘以电压纹波增益k1得到纹波电流的参考值i2wref。
2)DC-APF直流侧补偿电容电压控制。即补偿电容电压参考值uCref与实际值uC的差,经PI控制器调节得到纹波电流的参考值修正量iCref,从而维持DC-APF补偿电容电压的稳定。参考值i2wref和iCref的和为DC-APF纹波电流的参考值iLref。
3)DC-APF的补偿电流跟踪控制策略。采用基于改进的模糊自适应PI控制策略实现对补偿电流的跟踪控制。
2.1 基于小波变换Mallat算法的直流母线电压纹波检测法
直流母线电压中的纹波分量,其实质为在直流母线电压中含有交流分量。传统的检测方式是以低通滤波器提取出纹波分量,但低通滤波器在选取截止频率时,难以同时兼顾检测算法的检测精度和响应速度2项指标。选择较低的截止频率时,将提升算法的检测精度,却牺牲了算法的响应速度;反之,选择较高的截止频率时,将提高算法的响应速度,但牺牲了算法的检测精度。而小波变换不存在此问题,小波变换具有良好的时域-频域局部化特点,对不稳定成分很敏感,能够有效地将交流成分从直流电压中分离出来。Mallat算法是在多分辨率分析思想的基础上发展而来的,其实质为利用滤波器实现小波变换的快速算法[21]。通过选定合适的小波基,来确定滤波器系数。Daubechies(dbN)小波的特点是有良好的正则性,且随着阶次的增大,消失矩阶数就越大,其光滑性就越好,频域的局部化能力就越强,频带的划分效果就越好。基于以上优点,本文选用dbN小波。
首先,采用Mallat算法对采集到的直流母线电压信号进行分解[22]:
其中,cj+1(n)和dj+1(n)分别为对直流母线电压信号进行第j层小波分解后得到的近似分量和细节分量,低通滤波器系数用hj(k-2n)表示,高通滤波器系数用gj(k-2n)表示。采用Mallat算法对直流母线电压纹波进行检测,即根据不同的分辨率把采集到的直流母线电压信号分解到各个不同的子频段,然后对需要的子频段进行重构,可得到所需要的子频段内的信息;当直流母线电压信号分解到一定程度,其低频段的信息可认为是信号的基波分量。小波分解过程如图5 a)所示。
将各个子频段内的细节部分dj(n)即高频段信息设置为0,保留各自的近似部分cj(n)即低频段信息,之后对不同频域段的近似部分和细节部分进行多次重构,得到直流母线电压信号的基波,即直流母线电压中的直流分量信号,用直流母线电压信号减去直流分量信号,得到直流母线电压中的纹波分量信号。小波重构过程如图5 b)所示,直流母线电压信号的重构为
为验证该算法的有效性,根据小波分解重构公式在MATLAB编写程序,选用的小波函数为db3,并在MATLAB中模拟含有纹波分量的直流母线电压信号。采用文献[23—24]中的方法根据直流母线电压中的纹波频段分布范围和仿真中小波分解情况,来确定小波分解层数。由于本文主要针对直流母线电压中的二倍频纹波分量进行治理,即纹波分量的频段主要集中在100 Hz左右,因此设定直流母线电压信号u(t)由200 V的直流信号、峰值为1 V的 50 Hz交流信号、峰值为8 V的200 Hz交流信号、峰值为1 V的200 Hz交流信号叠加而成,即直流母线电压信号的频段为0~200 Hz。设其表达式为
首先,对u(t)采用db3的一层小波变换,并分解出低频系数信号c1(n)和高频系数信号d1(n),如图6 a)所示。然后,对低频系数c1(n)在进行4层小波变换后,此时c5(n)低频系数信号频段为0~6.25 Hz,频段已接近于直流母线电压的基波信号,且主要的交流信号已不在此范围之内,对低频系数c5(n)进行重构。如图6 b)所示,可以看出,重构后的c5(n)低频系数信号近似于基波信号,即只含有200 V的直流信号,综合直流母线电压中的纹波频段分布范围和仿真中小波分解情况,选定小波分解层数为5层;由原始信号u(t)减去c5(n)低频系数重构后的信号,得到原始信号中的纹波信号。如图6 b)所示,可以看出其幅值为8 V左右的交流信号,与设定的交流信号基本吻合,即本文所重构的表達式是有效且准确的。
将该算法应用到所设计的新型直流有源滤波器中,小波变换Mallat算法检测原理图如图7所示。选用的小波函数为db3,由上一步可知,对直流母线电压进行5层小波分解,可得到直流母线电压的基本信号,每一层分解都含有低通和高通2个通道,Lo band为低频通道(简称低通),Hi band为高频通道(简称高通),根据选定的小波函数bd3来设定参数,低通分解系数=
{0.035 2 0.085 4-0.135 0 -0.459 9 0.806 9 -0.332 7},5层分解后低频通道的输出值为直流母线电压的基波信号,将高频通道的输出值置零,只对低频通道输出部分进行小波重构,进行5次重构之后,得到直流母线电压中的直流分量,将其与直流母线电压相减,即得到直流母线电压中的纹波分量。
2.2 改进的模糊自适应PI控制策略
2.2.1 模糊PI控制器的设计
与传统PI控制器相比,模糊PI控制器不需要对被控对象建立准确的数学模型[25],可对PI参数进行在线调整,使控制系统具有良好的动、静态性能,可以更好地实现对补偿电流的跟踪控制。模糊PI控制器输入量为纹波电流参考值iref与补偿电流实际值iL的偏差e以及偏差变化率ec。通过模糊控制器得到比例参数调节量ΔKp和积分参数调节量ΔKi。
式(5)中Kp和Ki分别表示比例、积分参数;Kp0,Ki0分别为比例、积分参数的初始值。
根据相关专家经验结合参考文献[26]中模糊基本论域范围的确定方法,同时考虑本文仿真研究中直流负载电流的纹波幅度,最终选定偏差e的变化范围不大于给定值的6%,偏差变化率ec变化范围不大于偏差的10%,模糊控制器输出参数ΔKp和ΔKi的基本论域为控制系统中初始PI参数的20%左右。在仿真模型中,给定的直流负载电流值为10 A,因此偏差e的基本论域为[-0.6,0.6],偏差变化率ec基本论域为[-0.06,0.06];PI控制器初始参数按照临界振荡周期法取Kp0=1.2,Ki0=10,因此输出参数ΔKp的基本论域为[-0.24,0.24],输出参数ΔKi的基本论域为[-2,2]。模糊PI控制器输入端偏差e的模糊论域Ue={-3,-2,-1,0,1,2,3},输入端偏差变化率ec的模糊论域Ue={-0.6,-0.4,-0.2,0,0.2,0.4,0.6};输出端ΔKp的模糊论域
UΔKP={-0.3,-0.2,-0.1,0,0.1,0.2,0.3},输出端ΔKi的模糊论域UΔKi={-6,-4,-2,0,2,4,6};输入端e的量化因子Ke=3/0.6=5,输入端ec的量化因子Kec=0.6/0.06=10,输出端ΔKp的比例因子Ku=0.24/0.3=0.8,输出端ΔKi的比例因子Km=2/6=[SX(]1[]3[SX)]。模糊控制器输入、输出对应的语言变量是:
负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB),隶属度函数选三角函数,比例参数调节量ΔKp和积分参数调节量ΔKi的控制规则如表1所示。
本文选用重心法作为去模糊化方法,其精度较高,具有更平滑的输出推理控制。
2.2.2 改进的模糊自适应PI控制
模糊PI控制存在的问题:1)常规的模糊PI控制中,在设计隶属度函数时,一般是将每个语言变量进行均匀分布;即每个语言变量划分的论域范围相等,但并不符合实际情况[27]。此外隶属度函数的实质是反映函数的渐变性,因此,在此种方式下的误差较大。2)在DC-APF启动过程中,由于补偿电流和实际的纹波电流分量一直存在偏差,因而会导致积分项不断累加,引起积分饱和,造成较大的超调。3)模糊PI控制可以在一定程度上对PI控制器参数进行实时调整,但其调整的范围和幅度受限,且缺乏灵活性。现有文献中对模糊PI控制器的改进,主要是针对模糊控制规则、比例项、积分项和隶属度函数中的某一项进行改进[28]。
针对以上问题,本文进行了综合考虑,对语言变量的隶属度函数、比例项和积分项进行如下改进。
1)将语言变量改为不均匀分布,即越靠近0值时,隶属度函数曲线越陡;使系统在0值附近时,其控制策略更加敏感,从而提高补偿效果,如图8所示。
2)引入积分环节,先对误差的精确量进行积分,再和模糊控制器的输出变量进行叠加,构成总的输出量。由于积分的控制作用是根据误差的连续变化而连续变化的,因此可以进一步消除静态误差,加强系统的速动性。
3) 引入比例调整环节,对比例参数进行动态调整,来提高系统的响应速度。
改进的模糊自适应PI控制如图9所示。其中:iLref为纹波电流分量的参考值;iL为DC-APF生成的补偿电流分量;Kp0,Ki0分别为比例参数和积分参数的初始值;ΔKp和ΔKi为通过模糊控制器获得的比例参数和积分参数的修正量;Kp和Ki分别为经过模糊控制调整后的比例参数和积分参数;p1和p2为脉冲宽度调制(pulse width modulation,PWM)生成的控制脉冲。
改进的模糊自适应PI控制器的表达式为
式中:α为比例调整系数;e(t)为电流纹波的偏差输入量; Kii为引入的积分控制环节的积分参数。
由于模糊控制器的输入量只有偏差和偏差变化率,因此,其本身特性相当于一种系数时变的PD控制器,即控制器中缺少积分作用。其缺点是当系统负载变化时,模糊控制器难以有效消除稳态误差,控制精度不高。因此,本文在原有的控制方法上,加入一种对偏差的精确量积分环节,从而使整个控制系统的稳态性能得到提升。由PI控制理论可知,控制系统的响应速度和调节精度由比例系数Kp决定,当Kp越大时,响应越快,但是Kp过大则会导致系统产生超调,甚至会引起系统的不稳定;当Kp过小时,系统的响应会变慢,调节时间过长,影响整个系统的性能。
比例調整环节,即设置比例调节系数,对模糊控制修正后的比例参数进行进一步调节。考虑到PI参数的整定原则,比例调节系数应该与偏差的单调性相同,其整定原则是:当偏差较大时,通过增大比例调节系数,提升系统的响应速度;当偏差较小时,通过减小比例调整系数,起到防止系统超调的作用。即通过调整比例系数来控制比例参数的作用效果,提高系统的动态性能。本文采用阈值分割方法来设计比例调整系数α。
3 新型DC-APF应用于直流微电网的仿真验证
3.1 新型DC-APF应用于直流微电网的仿真模型
由于本文主要研究新型DC-APF对直流母线电压纹波的检测和抑制效果,因此,搭建了简化的DC-APF应用于直流微电网的仿真模型,如图10所示。直流微电网由模拟分布式电源模块、直流负荷构成,所设计的新型DC-APF直接接入直流微电网的直流母线,构成含DC-APF的直流微电网仿真模型。直流微电网通过双向DC-AC变换器连接到交流大电网,设置交流大电网中存在电压三相不对称,会使直流母线电压产生两倍频纹波分量[20]。本仿真中直流母线电压 200 V,直流电阻性负荷20 Ω; DC-APF中补偿电容电压250 V,滤波电感2 mH,直流侧电容2 200 μF;模拟分布式电源模块输出功率 2 000 W。
3.2 仿真结果分析
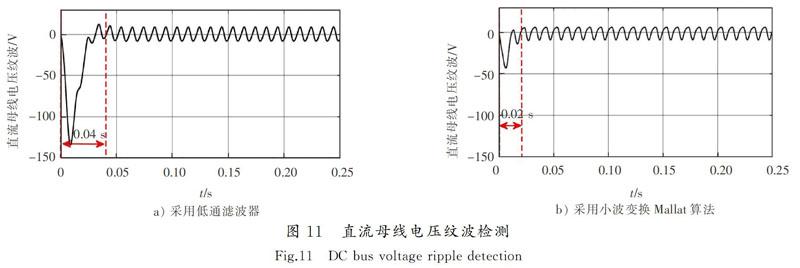
为验证所设计DC-APF的有效性,将传统纹波检测算法与所设计的纹波算法进行比较,结果如
图11所示。传统纹波检测主要依靠低通滤波器实现,本文低通滤波器的截止频率为30 Hz。由图11 a)可以看出,采用低通滤波器方法需要0.04 s左右才能获得较为准确的纹波,且超调较大;而采用小波变换Mallat算法只需要0.02 s左右即可分离出纹波,且超调较小,大大降低了延时,如图11 b)所示。
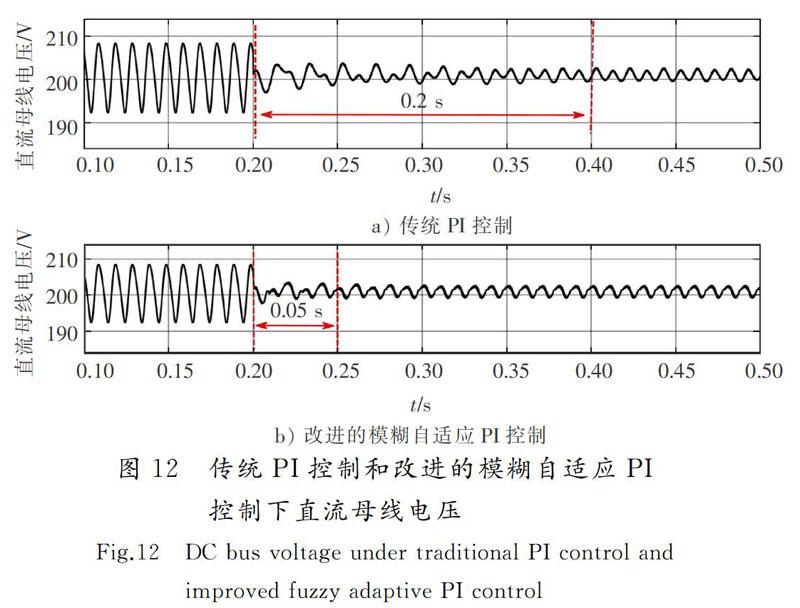
为验证所设计的补偿电流跟踪控制算法的有效性,将纹波检测方法均采用小波变换Mallat算法,在保证DC-APF其他参数不变的情况下,分别采用传统PI控制和改进的模糊自适应PI控制实现对补偿电流的跟踪控制,得到的直流母线电压波形如图12所示。在0.2 s左右時启动DC-APF,从图12 a)中可以看出,在传统PI控制下,DC-APF需要0.2 s才能实现对直流母线电压纹波的稳定抑制,即DC-APF的动态性能较差,且超调量较大。在改进的模糊自适应PI控制下,DC-APF只需0.05 s左右就能达到对直流母线电压纹波的稳定抑制,具有良好的动态性能,且超调量很小,对纹波的抑制效果更好。
图13为在改进的模糊自适应PI控制下直流负载电流、直流母线电压、补偿电流波形,0.2 s时启动DC-APF,通过产生补偿电流对直流母线电压纹波进行抑制。为了检验DC-APF对直流母线电压纹波的补偿效果,对DC-APF工作前后直流母线电压的变化进行了分析,如图13 b)所示,DC-APF工作前直流母线电压纹波的幅值约为8.3 V,纹波系数约为4.1%,在0.2 s时DC-APF启动,电压纹波的幅值约为1.6 V,纹波系数约为0.8%,可以看出,纹波系数明显降低。
对DC-APF启动前后直流负载电流的纹波含量进行快速傅里叶变换(fast fourier transform,FFT)分析,结果见图14,DC-APF工作前,直流负荷电流纹波的总谐波畸变率(total harmonic distortion,THD)为4.62%,DC-APF工作后,直流负载电流纹波的THD值降为0.72%。可以看出,直流负载电流中的纹波分量得到了明显降低。
4 结 语
1)针对直流母线电压存在的纹波分量会对整个直流微电网的供电质量以及设备运行安全性造成影响的问题,提出了一种新型直流有源滤波器控制策略对直流母线电压纹波进行抑制。
2)在分析了DC-APF多种工作模态的基础上,针对传统直流母线电压纹波检测算法存在延迟性的问题,提出了基于小波变换Mallat算法的直流母线电压纹波检测法。为验证算法的有效性,根据小波分解重构公式在MATLAB编写程序,对模拟的直流母线电压纹波信号进行检测,再将该算法应用到所设计的新型直流有源滤波器中用以提取直流母线中的纹波分量。
3)采用改进的模糊自适应PI控制,实现了对补偿电流的跟踪控制。
4)搭建了含DC-APF的直流微电网系统模型,对新型DC-APF控制策略进行仿真验证。结果表明,与传统纹波检测方法相比,本文所提出的检测方法实时性更好,与传统补偿电流的跟踪控制方法相比,具有更好的动态性能。
5)本研究不足之处在于未对DC-APF直流侧电容电压控制方法展开探讨,后续工作将针对这一问题及DC-APF的容错型拓扑结构与控制方法展开研究,用于进一步提高DC-APF的纹波抑制效果及工作可靠性。
参考文献/References:
[1] 蒋翔宇.交直流混合微电网中直流母线电压的波动控制研究[D].济南:山东大学,2019.
JIANG Xiangyu. Research on Voltage Fluctuation Control of DC Bus in AC/DC Hybrid Microgrid [D]. Jinan: Shandong University, 2019.
[2] 周小平,罗安,陈燕东,等.直流微电网中双向储能变换器的二次纹波电流抑制与不均衡控制策略[J].电网技术,2016,40(9):2682-2688.
ZHOU Xiaoping, LUO An, CHEN Yandong, et al. Secondary ripple current suppression and imbalanced control strategy in bidirectional storage converter of DC microgrid [J]. Power system Technology,2016,40(9):2682-2688.
[3] KUMAR D, ZARE F, GHOSH A. DC microgrid technology: System architectures, AC grid interfaces, grounding schemes, power quality, communication networks, applications, and standardizations aspects[J]. IEEE Access, 2017, 5: 12230-12256.
[4] SWAIN S D, RAY P K, MOHANTY K B. Improvement of power quality using a robust hybrid series active power filter[J]. IEEE Transactions on Power Electronics, 2017, 30(5): 3490-3498.
[5] JIA Qi, YU Yong, LI Yijia, et al. An impedance-match design scheme for inductively active power filter in distribution networks[J]. International Journal of Electrical Power and Energy Systems,2018,99: 638-649.
[6] ZAFARI A, JAZAERI M. Conceptual design of an efficient unified shunt active power filter based on voltage and current source converters[J]. Energy,2017,119: 911-925.
[7] 施烨,吴在军,窦晓波,等.基于自适应原理的改进型FBD谐波电流检测算法[J].电网技术,2014,38(4):1051-1058.
SHI Ye, WU Zaijun, DOU Xiaobo, et al. Adaptive theory based improved FBD algorithm for harmonic current detection[J]. Power System Technology, 2014,38(4): 1051-1058.
[8] SHEIKH S, NUNO H, ANTONIO G, et al. Analog active filter design using a multi objective genetic algorithm[J]. AEUE-International Journal of Electronics and Communications,2018,93: 83-94.
[9] LI S, LEE A T L, TAN S C. A plug-and-play ripple mitigation approach for DC-links in hybrid systems[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC). Long Beach: IEEE, 2016: 169-176.
[10]WANG Ruxi, BOROYEVICH F, BURGOS D, et al. A high power density single-phase PWM rectifier with active ripple energy storage[J]. IEEE Transactions on Power Electronics, 2011, 26(5): 1430-1443.
[11]陳仲,许亚明,王志辉,等.航空高压直流电网低频纹波的有源抑制[J].电工技术学报,2015,30(20):151-158.
CHEN Zhong, XU Yaming, WANG Zhihui, et al. Active inhibition of the low frequency ripple in aeronautical high voltage DC power system[J]. Transactions of China Electrotechnical Society,2015, 30(20): 151-158.
[12]王磊,曹现峰,刘小宁,等.基于能量回馈和注入补偿的直流有源滤波器设计[J].高电压技术,2013,39(11):2756-2761.
WANG Lei, CAO Xianfeng, LIU Xiaoning, et al. Design of DC active filter based on energy feedback and injection compensation[J]. High Voltage Engineering, 2013, 39(11): 2756-2761.
[13]黄海宏,刘亚云,王海欣,等.H桥级联型APF直流侧电压平衡三级控制[J].电机与控制学报,2018,22(1):77-85.
HUANG Haihong, LIU Yayun, WANG Haixin, et al. Three-level equilibrium strategy of DC voltage balance control of H-bridge cascade APF[J]. Electric Machines and Control, 2018, 22(1): 77-85.
[14]CHEN Zhong, CHEN Miao, LUO Yingpeng, et al. Low frequency ripple current compensation with DC active filter for the single-phase aeronautic static inverter[C]//2011 IEEE Energy Conversion Congress and Exposition. Phoenix: IEEE, 2011:1468-1475.
[15]郭振,乐全明,郭力,等.交直流混合微电网中直流母线电压纹波抑制方法[J].电网技术,2017,41(9):2896-2904.
GUO Zhen, LE Quanming, GUO Li, et al. Control method of DC bus voltage ripple mitigation in hybrid AC/DC microgrid[J]. Power System Technology, 2017, 41(9): 2896-2904.
[16]车志霞,张朋飞,车志飞.基于PI+重复控制的三相四桥臂有源电力滤波器的研究[J].石家莊铁道大学学报(自然科学版),2019,32(3):120-126.
CHE Zhixia, ZHANG Pengfei, CHE Zhifei. Research on three-phase four-leg active power filter based on PI+ repetitive control[J]. Journal of Shijiazhuang Railway University (Natural Science Edition),2019,32(3):120-126.
[17]孙正,李可军,袁沔齐,等.基于系统辨识的HVDC直流有源滤波器重复控制方法研究[J].电力系统保护与控制,2012,40(24):143-149.
SUN Zheng, LI Kejun, YUAN Mengqi, et al. Research on the repeated control method of DC active power filter in HVDC based on system identification[J]. Power System Protection and Control,2012,40(24):143-149.
[18]李红波,张凯,赵晖.高功率密度单相变换器的直流有源滤波器研究[J].中国电机工程学报,2012,32(15):40-47.
LI Hongbo, ZHANG Kai, ZHAO Hui. Researches on DC active filter for high power density single phase converters [J]. Proceedings of the CSEE, 2012, 32(15): 40-47.
[19]FEI J, WANG H. Fractional-order adaptive recurrent neural sliding mode control of active power filter[C]//2019 20th International Symposium on Power Electronics. Novi Sad:IEEE, 2019: 1-6.
[20]郭振. 交直流微电网控制策略和直流母线电压纹波治理方法研究[D].天津:天津大学,2018.
GUO Zhen.A Research of Control Strategy for AC/DC Microgrids and Surppression Method for DC Bus Voltage Oscillation[D]. Tianjing: Tianjin University, 2018.
[21]金攀,雷景生.基于快速傅里叶变换和db小波变换的谐波检测[J].上海电力学院学报,2017,33(4):337-340.
JIN Pan, LEI Jingsheng. Harmonic detection based on FFT and db wavelet transform [J]. Journal of Shanghai Electric Power University, 2017, 33 (4): 337-340.
[22]雷汝海,郝震.基于小波变换Mallat算法的电网谐波检测方法[J].工矿自动化,2014,40(12):65-69.
LEI Ruhai, HAO Zhen. A harmonic detection method for power network based on wavelet transform Mallat algorithm [J]. Industrial and Mine Automation, 2014, 40(12): 65-69.
[23]郭晓玲,程建.基于小波分析的有源滤波器技术研究[J].核电子学与探测技术,2014,34(3):285-289.
GUO Xiaoling, CHENG Jian. Research on technology of wavelet-based active power filter[J]. Nuclear Electronics and Detection Technology, 2014, 34(3): 285-289.
[24]朱翔,解大,高强,等.基于FFT和db20小波变换的电力系统谐波联合分析策略[J].电力系统保护与控制,2012,40(12):62-65.
ZHU Xiang, XIE Da, GAO Qiang, et al. Analyzing strategy for power system harmonic based on FFT and DWT using db20[J]. Power System Protection and Control, 2012, 40(12): 62-65.
[25]NASYROV R R, ALJENDY R I. Comprehensive comparison between hybrid fuzzy-PI and PSO-PI controllers based active power filter for compensation of harmonics and reactive power under different load conditions[C]//2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering. Moscow: IEEE, 2018: 725-730.
[26]徐奔奔,周芝峰,霍文明,等.基于改进的模糊控制PMSM矢量控制系统研究[J].电力科学与工程,2016,32(3):1-6.
XU Benben, ZHOU Zhifeng, HUO Wenming, et al. The research of PMSM vector control system based on improved fuzzy control[J]. Electric Power Science and Engineering, 2016, 32(3): 1-6.
[27]ZHAO Zhenxing, LIU Fugui, WANG Yangang. Research on the application of improved fuzzy-PI control in STATCOM[J]. Science Discovery, 2016, 4(1): 39-44.
[28]胡堂清,張旭秀.基于改进模糊PI控制器的PMSM矢量控制系统仿真[J].自动化与仪表,2019,34(6):91-95.
HU Tangqing, ZHANG Xuxiu. PMSM vector control system simulation based on improved fuzzy PI controller [J]. Automation and Instrumentation, 2019, 34(6): 91-95.

