复杂滑坡三维离散建模方法及其在茂县滑坡中的应用*
陈 骎 范 刚② 周家文②
(①四川大学水利水电学院,成都610065,中国)
(②四川大学水力学与山区河流开发保护国家重点实验室,成都610065,中国)
0 引 言
数值模拟可以重现滑坡破坏和失效后的复杂运动过程,是研究滑坡灾害的重要手段之一(杜鹃等,2015;李萌等,2018;马鹏辉等,2018;施家杰等,2019)。3DEC(Three-dimensional Distinct Element Code)是一款由美国Itasca公司开发的三维块体离散元计算软件,采用显示差分法进行求解运动方程,能够准确地模拟外力作用下块体的运动过程(Hart et al.,1988)。相对于基于连续介质力学的数值方法(如FEM、FLAC等)和基于颗粒离散元的数值方法(如PFC、EDEM等),3DEC中的块体接触模型能够更加准确地反映块体间的相互作用,因此,3DEC更适用于滑坡的运动过程模拟(顾金等,2016;Wu et al.,2017,2018;Shen et al.,2019)。
建立几何模型是进行数值模拟的第一步,3DEC软件对于复杂几何模型的建模提供了以下两种方法:(1)在Rhinoceros软件中建立边坡solid实体,导出为VRML格式文件,再由内置的VTPT插件将其转为3DEC命令流;(2)通过Gridle插件将AutoCAD创建的闭合几何图形转换为3DEC块体(Itasca Consulting Group,Inc.,2016)。3DEC提供的两种建模方法难以满足复杂滑坡数值模拟快速建模的要求。为了克服3DEC软件在建模方面的不足,一些学者进行了一些探索。韩浩亮等(2012)利用Surfer软件和FISH语言编程,建立了复杂地表及简单地层的地质体模型。赵玉玲等(2018)采用MATLAB建立了复杂矿区的地表模型。石崇等(2016)提出一种自下向上的建模方法,利用AutoCAD、ANSYS软件及FORTRAN语言实现了具有复杂坡面形态边坡的模型构建。
滑坡数值分析模型通常可分为滑床、滑体两个部分,但是,对于高速滑坡而言,运动过程中常常伴随有强烈的铲刮现象,建模时还应考虑滑动路径上的基底物质。一方面,滑动路径上的基底物质将影响滑坡物源的运动轨迹及运动距离;另一方面,由于基底物质的存在,滑坡灾害往往体现出放大效应,滑坡堆积区的物质量远大于物源区的物质量(周家文等,2019)。因此,对滑坡运动路径上的基底物质进行精确建模并准确模拟滑坡失稳过程中的铲刮效应是模拟滑坡灾害的关键。赵玉玲等(2018)所提出的方法只适用于简单的滑坡建模,难以实现滑坡体和松散基底物质的建模。韩浩亮等(2012)和石崇等(2016)提出的方法难以对基底物质进行建模,且要使用多个软件耦合建模与编程,过程较复杂。本文在总结前人经验的基础上,提出了基于MATLAB平台的3DEC复杂滑坡模型的前处理方法,并以四川省茂县新磨村滑坡为例详细叙述了滑坡模型建模步骤,对类似的滑坡运动过程模拟有一定的参考借鉴意义。
1 复杂滑坡建模方法
1.1 块体模型生成
本方法采用三棱柱块体构建滑床与滑体,利用Voronoi多面体模拟滑动路径上的基底物质。下边对上述2类块体模型生成方法分别介绍。
1.1.1 三棱柱体生成
Distmesh是一款开源的MATLAB网格划分工具箱(Persson et al.,2004),可对任意形状的多边形进行三角网格剖分。通过其中的distmesh2D函数生成二维三角网格,输出结果为包含所有节点坐标和各个三角单元节点序号的数组。
进一步以滑坡前、后的表面点云三维坐标为基础,通过线性插值得到网格节点的高程坐标,将二维网格扩展到三维。对于构成滑床的三棱柱块体,下表面节点的高程指定为一常数,上表面节点的高程由滑坡后地表点云进行插值得到。对于构成滑体的三棱柱块体,下表面即为滑动面,其高程由滑坡后的地表点云进行插值得到,上表面节点的高程由滑坡后的地表点云进行插值得到。需要注意的是,由于插值引入误差以及坐标数据误差的影响,可能出现上表面点高程低于下表面对应点高程的情况,因此在插值后需对高程进行检查,若上表面点高程小于下表面点对应高程,则需对高程进行修正,本文方法取上表面点高程等于下表面点高程加上0.1im。生成的三棱柱体示意图(图1)。
1.1.2 Voronoi多面体生成
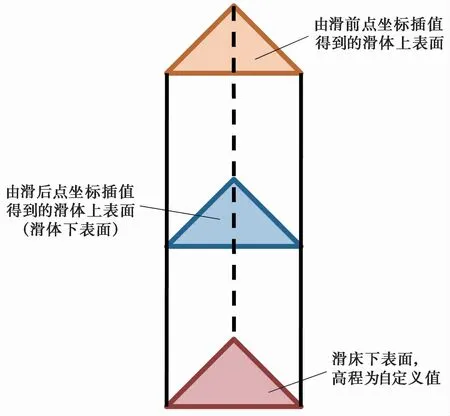
图1 插值得到的三棱柱体Fig.1 Triangular prism generated by interpolation
MPT(Multi-Parametric Toolbox 3.0)是 在MATLAB环境下开发的用于约束最优控制器建模、控制、分析和部署的算法集合(Herceg et al.,2013)。它有一个强大的几何库,其将工具箱的应用扩展至优化控制之外,以解决计算几何中出现的各种问题。由几何库中的mpt_voronoi函数可生成一系列Voronoi多面体。函数通过在指定凸多面体区域内部进行Voronoi划分以达到生成多个Voronoi多面体的目的,区域边界由凸多面体的顶点控制,生成多面体的尺寸由外边界与输入凸多面体中心坐标决定,生成的凸多面体数量与输入多面体中心坐标数相同。mpt_voronoi函数的输出结果中包含有各多面体的顶点坐标。
1.2 块体拓扑信息获取
描述一个三维块体结构,必须明确其包含的点、线、面间的拓扑关系。以3DEC中的块体生成命令poly face为例,多面体由带有face关键字的平面构成,其中顶点坐标(x1,y1,z1),(x2,y2,z2)等定义了面的边界,并且顶点必须按顺时针顺序输入(从块外部观察块面)。为此,需首先获取块体的所有面及面上点的信息,再将各面上点的坐标进行顺时针排序。对于三棱柱体,上、下表面的节点序在之前的网格划分与插值后已经存在,对上、下表面的节点进行两两组合,得到3个侧面的节点序号;而由MPT工具箱生成的Voronoi多面体P,由不等式组(1)定义:
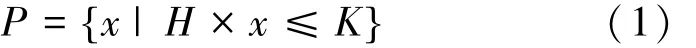
式中:x为多面体内部及面上的点坐标;H为m×3矩阵;m为多面体面的数量,矩阵的每一行为对应面的法向量,H×x=K即包含m个面的平面方程。计算所有顶点到每个面的距离,若距离为0,则此点位于该面上,通过循环计算即可获取每个面所包含点的坐标。使用MATLAB中的二维cell数组来存放2类块体的拓扑信息,每个块体的信息按行进行存放,每个面的信息按列存放,每个非空的cell单元为n行3列的数组,用来存放每个面上n个节点的三维坐标。
接着对各面上的点进行顺时针排序,对以上2类块体均采用同一算法进行顶点排序。上述2类块体皆为凸多面体,均由凸多边形表面构成,故只需对表面局部坐标系下的顶点按极角大小排序即可。如图2所示,以Voronoi多面体为例,在多面体表面内建立局部坐标系,以凸多边形表面内一点O为局部坐标系原点(本方法取各顶点坐标平均值),极轴方向为原点O指向该cell单元中第一个点P1方向,并记第一点的极角为0°,图2中点C可为多面体内部任意一点(本方法C点坐标取多面体所有顶点坐标的平均值)。该cell单元中第n(n>1)个点Pn的极角α按式(2)计算:
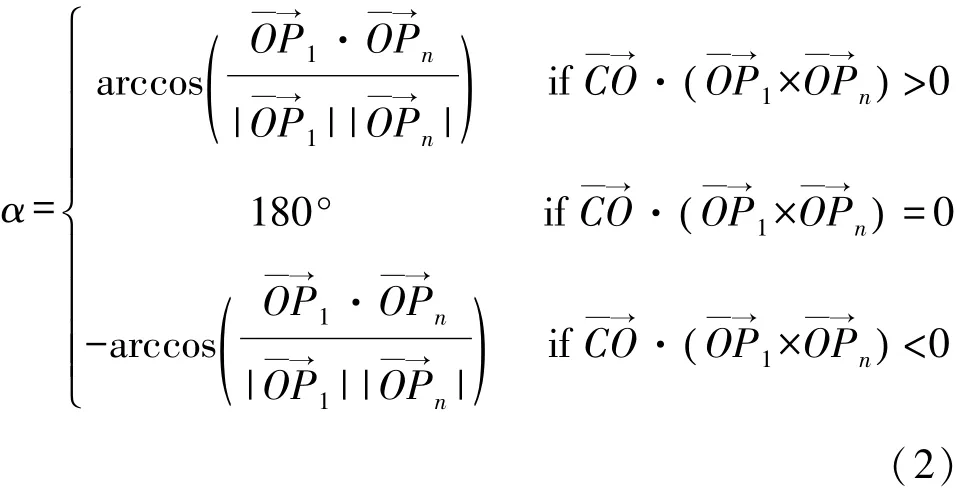
最后按极角由大到小对各点重新排序,即实现面上点的顺时针排序。
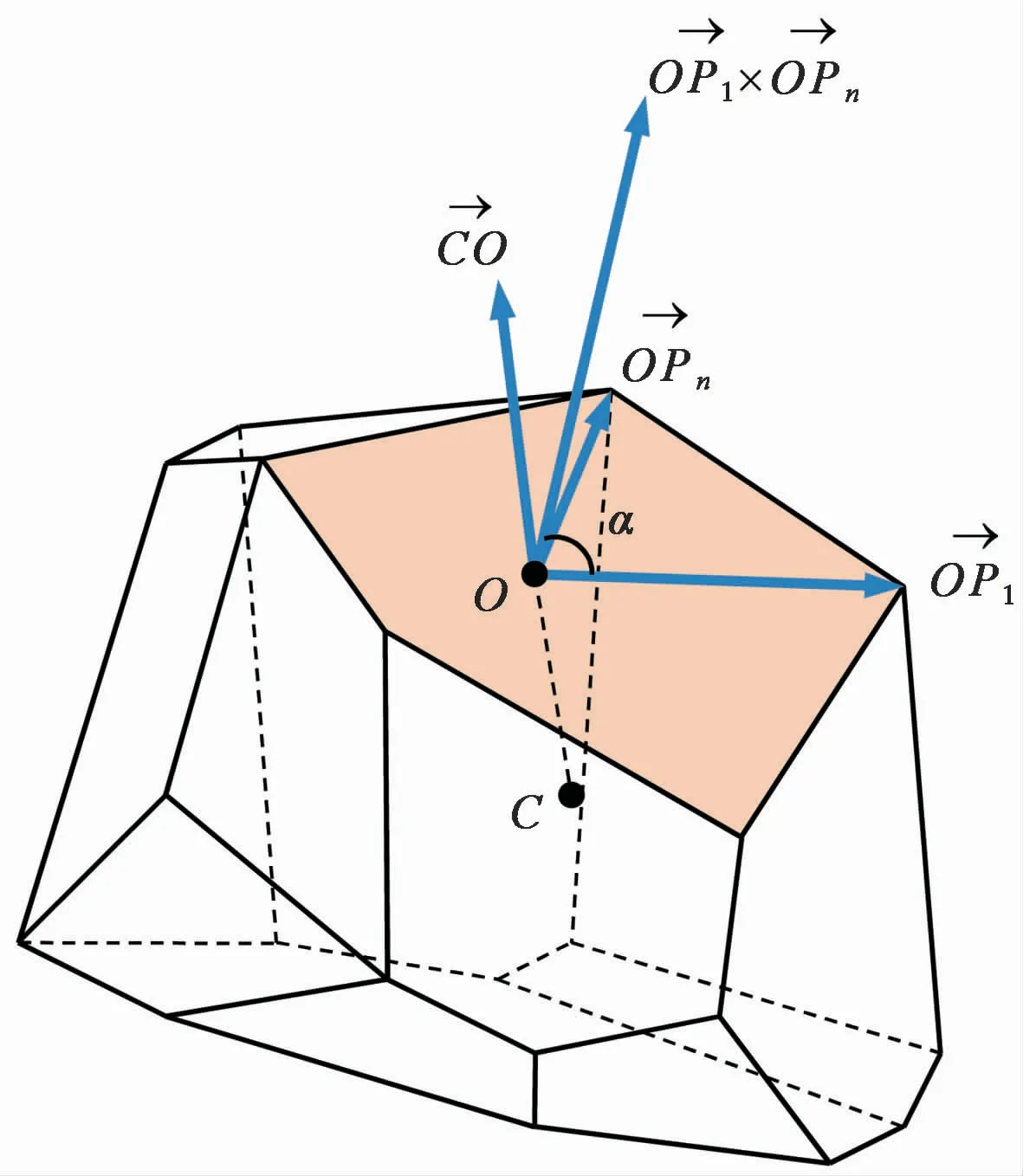
图2 面上点顺时针排序示意图Fig.2 Schematic diagram of clockwise sorting of points on the surface
1.3 3DEC命令输出
将存放于cell数组中的块体坐标信息写成满足3DEC语法要求的命令流,并输出为txt格式文本。poly prism是3DEC中专用于生成棱柱形块体的命令,由于只需要输入棱柱上下两个面的顶点坐标,相比poly face命令更加简便,读取速度更快,韩浩亮等(2012)和赵玉玲等(2018)提出的方法均按poly prism命令格式输出。但在实际运用中发现,当棱柱上、下表面距离很近时,3DEC中无法生成棱柱形的滑体。为避免这一缺陷,三棱柱体与Voronoi多面体均按poly face命令要求的格式输出。
1.4 复杂滑坡建模实现方法
综上所述,本研究提出的复杂滑坡的建模实现方法主要包括以下几个步骤:
(1)进行块体生成。采用三棱柱体构建滑床与滑体,通过Distmesh工具将滑坡区域划分为二维三角网格并通过高程插值将二维三角面拓展为三棱柱体。采用Voronoi多面体构建基底物质,通过MPT工具箱生成Voronoi多面体。
(2)进行块体拓扑信息的获取。通过节点组合的方式获取三棱柱面的信息,通过判断点与面的间距获取Voronoi多面体面的信息,随后对2类多面体面上点进行顺时针排序。
(3)接着按poly face命令格式将块体的拓扑信息转化输出为3DEC命令流文本文件。
(4)最后在3DEC中调用块体生成命令流文本文件,即实现滑坡模型的建立。
复杂滑坡的建模方法步骤流程图(图3)。
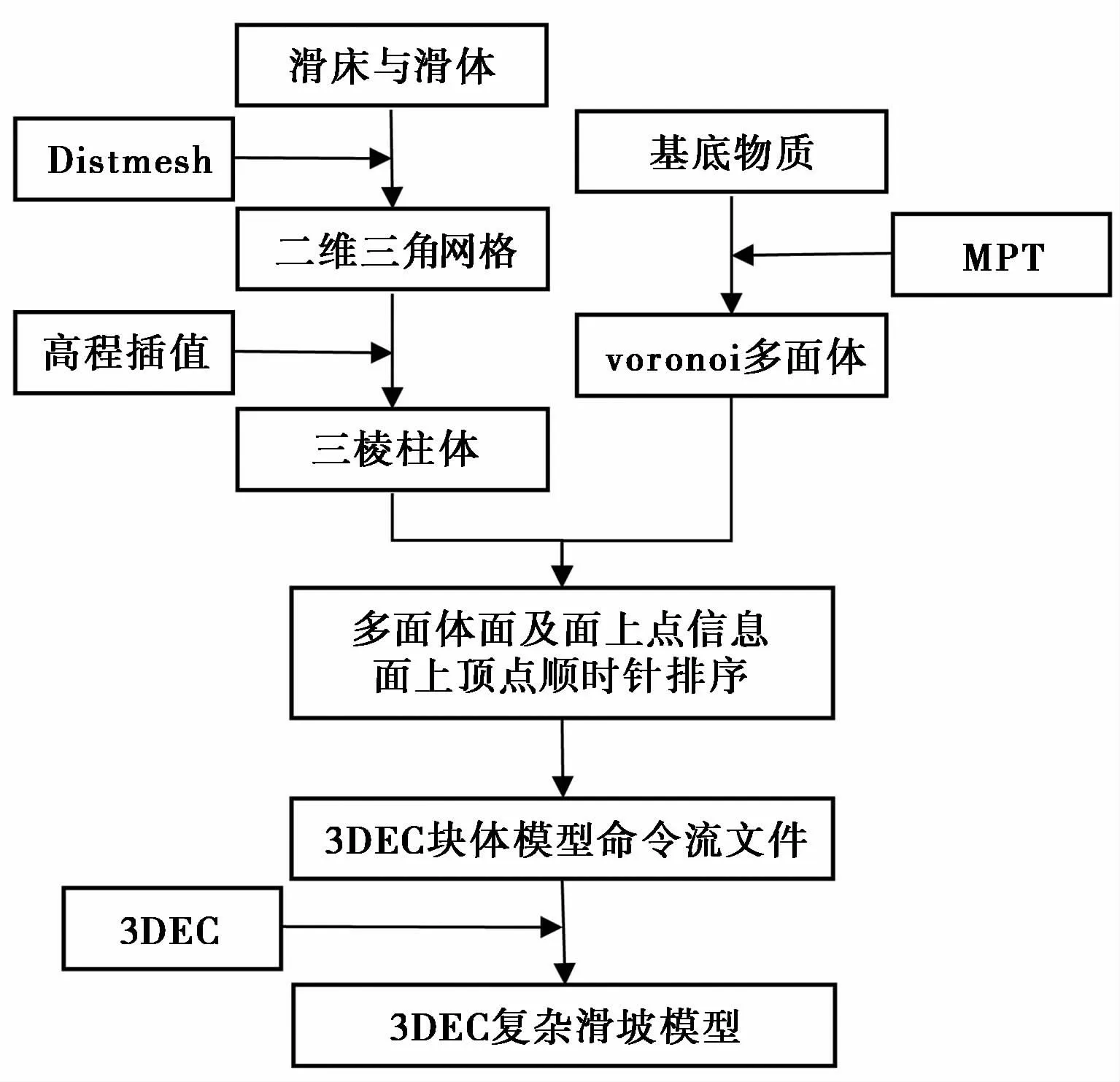
图3 滑坡建模流程图Fig.3 Landslide modeling flow diagram
2 建模函数
为实现3DEC复杂滑坡建模,依据上节提出的复杂滑坡建模方法编写了相应的MATLAB函数。本节对建模过程中涉及的Distmesh、MPT工具箱中的部分函数及自编函数进行介绍。
2.1 Distmesh中的函数
2.1.1 function d=drectangle(p,x1,x2,y1,y2)
本函数功能是计算平面点到矩形边界的最短距离。输入p为n×2的数组,存有n个点的x,y坐标;函数输入参数x1,x2,y1,y2决定了矩形区域的4个顶点坐标(x1,y1)(x1,y2)(x2,y1)(x2,y2)。函数输出d为包含n个点到矩形边界距离的列向量,若点在矩形内部,则距离为负,反之则为正。
2.1.2 function d=dpoly(p,pv)
本函数功能是计算平面点到多边形边界的最短距离。输入p为n×2的数组,存有n个点的x,y坐标;输入pv为m×2的数组,为多边形的m个顶点坐标。函数输出d为包含n个点到多边形边界距离的列向量,若点在多边形内部,则距离为负,反之则为正。
2.1.3 function d=ddiff(d1,d2)
本函数功能是取d为d1与-d2中各行元素的较大值。函数输入参数d1与d2为两个行数相同的列向量。函数输出为与d1、d2行数相同的列向量。
2.1.4 function[p,t]=distmesh2id(fd,fh,h0,bbox,pfix,varargin)
本函数功能为在指定区域内生成三角形网格。函数输入参数fd为点到网格边界的距离函数,用以指定生成网格的区域边界;输入参数fh为确定网格节点间距的函数,用以决定网格的边长;h0为网格节点间距的初始值;bbox为2×2数组[x min,y min;x max,y max],表示生成初始网格节点的矩形区域,(x min,y min)、(x max,y max)为矩形的两个顶点;pfix为n×2数组,表示固定的节点坐标;varargin为fd、fh函数的额外参数。函数输出p为N×2数组,包含N个节点的x,y坐标;t为M×3数组,每行表示M个单元的3个节点序号。
2.2 MPT中的函数
2.2.1 function P=polytope(V)
本函数功能为生成一个凸多面体。函数输入参数V为n×3数组,存有凸多面体n个顶点的x,y,z坐标。函数输出P为polytope结构体,成员P.H与P.K分别为m×3和m×1数组,m为多面体面的个数,P={x|H×x≤K}定义了P的范围;成员P.V为n×3数组,存有凸多面体n个顶点的空间坐标。
2.2.2 function Pn=mpt_voronoi(points,Options)
本函数功能为在指定的边界内生成Voronoi多面体。函数输入参数points为n×3数组,作为生成n个Voronoi多面体的中心坐标;函数输入参数Options为结构体,成员Options.bound为polytope结构,作为多面体生成的边界,成员Options.plot为1则绘制生成的Voronoi图,为0则不绘图。函数输出Pn为n×1数组,n为生成多面体的个数,数组中每个元素为一个polytope结构体。
2.3 自编函数
2.3.1 function pu=interpo(pb,po)
本函数功能是利用下表面网格节点的平面坐标插值得到上表面网格节点的高程。函数输入参数pb为下表面网格的节点坐标值,为n×3数组,po为插值需要的上表面节点坐标,为m×3数组。函数输出pu为插值得到的平面坐标与pb对应上表面节点坐标,为n×3数组。n为网格节点数目,m为原地形空间坐标点数目。
2.3.2 function C=triprism(t,pu,pl)
本函数功能是根据上、下表面的点序号与点坐标值生成包含5个面的cell数组。函数输入参数t为M×3数组,每行表示各个单元的3个节点序号,输入参数pu为n×3数组,包含上表面网格节点的三维坐标,输入参数pb为pu对应的下表面网格节点坐标数组。函数输出C为M×5的cell数组,包含各三棱柱体的面与点信息。n为网格节点数目,M为三棱柱体数目。
2.3.3 function C=voronoiface(Pn)
本函数功能为生成Voronoi多面体cell数组。函数输入参数Pn为M×1数组,其数组单元为polytope结构体。函数输出C为M×N的cell数组,M为Voronoi多面体的个数,N为各个多面体所包含面的数量的最大值。
2.3.4 function C=clockwise(C)
本函数功能为对数组C中每一单元(对应多面体的面)中的点进行顺时针排序。
2.3.5 function C=transfer(C,k,t,r)
本函数功能为对多面体进行缩放、平移和旋转。函数输入参数C为表示多面体的cell数组,k为缩放比例,t为1×3平移向量,包含沿x,y,z方向的移动距离,r为1×3向量,包含绕x,y,z轴的旋转角度。函数输出C为多面体进行缩放、平移和旋转后的cell数组。
2.3.6 function polyface(C,filename)
本函数功能为将多面体拓扑信息输出为3DEC命令流。输入C为示多面体的cell数组,函数输入参数filename为输出路径与文件名。函数输出结果为指定路径与名称的txt格式文件。
3 实例应用
新磨村滑坡位于四川省茂县叠溪镇新磨村(坐标东经103°39′46″,北纬32°4′47″),为一典型高位顺层岩质滑坡,滑坡于2017年6月24日失稳,共计造成83人死亡或失踪,滑体堵塞松坪沟,形成堰塞湖(许强等,2017)。如图4所示,滑源区位于松坪沟左岸富贵山西坡山脊处,滑体顶部高程3460im,剪出口高程约为3100im,滑动面平均坡度约47°。滑源区长和宽约分别为200im和300im,平均厚度约46im,体积约为450×104im3。滑源区出露基岩为三叠系中统杂谷脑组(T2z)变质砂岩夹板岩,岩层面产状为N70°W/SW∠51°,构成滑体的底部边界。滑源区岩体内发育有2组结构面,产状分别为N7°E/NW∠71°和N40°E/NW∠29°,前者构成滑体的两侧边界(Su et al.,2017)。滑源区以下存在明显的流通铲刮区,流通铲刮区主要为崩坡积碎石土,由岩块、砾石和1933年叠溪地震诱发的古滑坡堆积体等组成,分布高程为2650~3100im,长度和宽度约分别为700im和410im,平均铲刮深度约30im。滑体在向下运动中强烈刮铲坡面原有松散堆积物,滑体体积不断增大,最终形成总体积约为1300×104m3的滑坡堆积体。堆积体位于2650im高程以下至2300 m高程区域,呈扇形堆积,顺滑向长度约1600im,顺河向最大宽度为1080im。通过比较滑坡前后地形高程变化,滑坡的平均堆积厚度大于10 m,最大堆积厚度约为31 m(图5)。
本文以新磨村滑坡为例,详细叙述复杂滑坡的建模方法。
(1)数据准备。准备滑坡发生前、后的地表点坐标数据(可从CAD文件等高线数据中提取),供生网格节点高程插值使用,保存为txt格式文件,每行存放一个点的三维坐标数据。选取滑源区、流通铲刮区边界上的点,作为滑源区、流通铲刮区网格划分的边界。
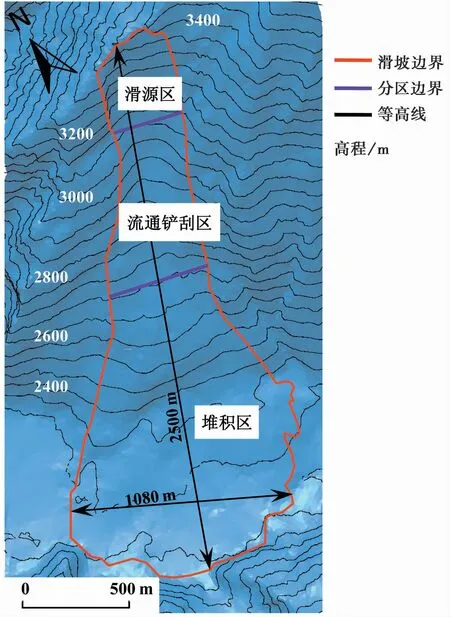
图4 新磨村滑坡滑后数字高程模型Fig.4 Digital elevation model of Xinmo landslide after sliding
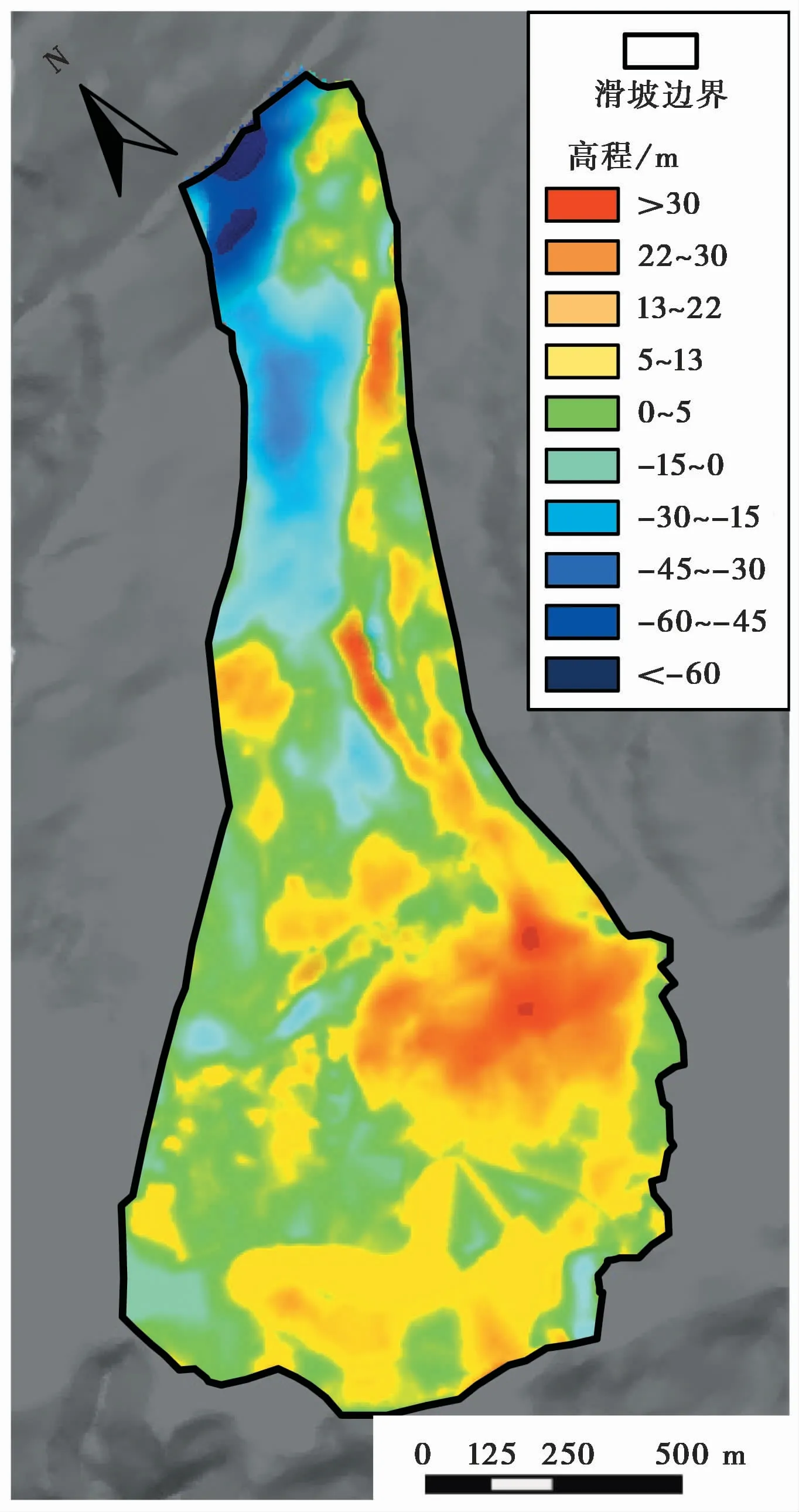
图5 新磨滑坡高程变化图Fig.5 Elevation variation of Xinmo landslide
(2)三角形网格划分。读取滑源区、流通铲刮区边界点文件并命名为bound1和bound2,滑源区和流通铲刮区边界点的命名为bound3。bound1为滑源区的外边界,bound2为流通铲刮区的外边界,bound3为滑源区与流通铲刮区的共同边界,整个模型的外边界为一矩形,用ddiff函数计算内、外区域的差集。采用distmesh2d函数进行3个区域的网格划分,网格边长统一为40im。可在MATLAB中绘制网格并进行网格质量检查,生成的网格如图6所示。进一步设置模型的底部高程为2000im,将二维三角网格转化为三维网格。MATLAB命令如下:
>>bound1=load(′E:\滑源区边界.txt′);
>>bound2=load(′E:\流通铲刮区边界.txt′);
>>bound3=load(′E:\内边界.txt′);
>>[pb1,t1]=distmesh2id(@dpoly,@huniform,40,[270,1600;750,2900],bound1,bound1);
>>[pb2,t2]=distmesh2id(@dpoly,@huniform,40,[270,1600;750,2900],bound2,bound2);
>>fd=inline(′ddiff(drectangle(pb3,-40,1370,10,2950),dpoly(pb3,bound3))′,′pb3′,′bound3′);
>>pfix=[bound3;1370,2950;1370,10;-40,2950;-40,10];
>>[pb3,t3]=distmesh2id(fd,@huniform,40,[-40,10;1370,2950],pfix,bound3);
>>len=[size(pb1,1),size(pb2,1),size(pb3,1)];
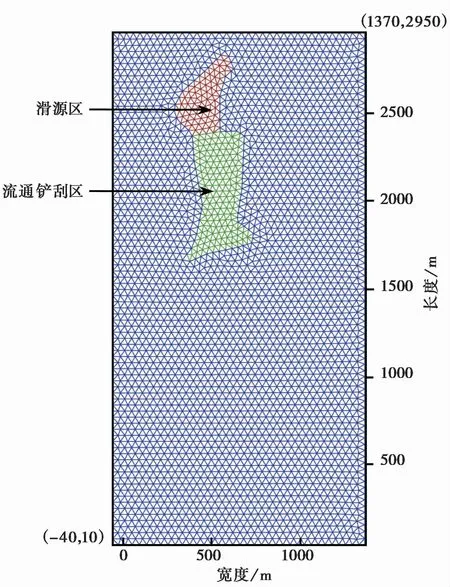
图6 Distmesh生成的三角网格Fig.6 Triangle meshes generated with Distmesh
>>pb1=[pb1,2000*ones(len(1),1)];
>>pb2=[pb2,2000*ones(len(2),1)];
>>pb3=[pb3,2000*ones(len(3),1)];
(3)底部地形建模。对于滑源区和流通区,上表面网格高程用滑后点云插值得到,对于外部区域,上表面网格用滑前点云插值得到。面上点顺时针排序,输出为3DEC命令文本。MATLAB命令如下:
>>pre_surface=load(′E:\滑前.txt′);
>>post_surface=load(′E:\滑后.txt′);
>>pu1=interpo(pb1,post_surface);
>>pu2=interpo(pb2,post_surface);
>>pu3=interpo(pb3,pre_surface);
>>C1=triprism(t1,pu1,pb1);C2=triprism(t2,pu2,pb2);
>>C3=triprism(t3,pu3,pb3);
>>base=[C1;C2;C3];base=clockwise(base);
>>polyface(base,′E:\base_3DEC.txt′);
(4)滑体建模。滑源区下表面网格采用上一步插值得到的t1与pu1,上表面网格利用滑前点云插值得到。对C4重新排序,设置输出路径与文件名,输出为3DEC命令文本。MATLAB命令如下:
>>t4=t1;pb4=pu1;
>>pu4=interpo(pb4,pre_surface);
>>C4=triprism(t4,pu4,pb4);
>>C4=clockwise(C4);
>>polyface(C4,′E:\source_3DEC.txt′);
(5)流通铲刮区堆积体建模。在长、宽、高分别为500im、300im、50im的长方体区域内生成7500个Voronoi多面体。接着对所有多面体的面及面上的点进行计算、顺时针排序。为产生堆积体松散堆积状态,使块体在重力作用下进行堆积,在输出为3DEC命令文本前对块体进行平移与旋转。MATLAB命令如下:
>>P=polytope([0,0i0;300,0i0;300,500,0;0,500,0;0,0i50;300,0i50;300,500,50;0,500,50]);
>>Options.plot=1;Options.pbound=P;
>>points=[300*rand(1,7500);500*rand(1,7500);50*rand(1,7500)];
>>Pn=mpt_voronoi(points′,Options);
>>polytopes=voronoi_face(Pn);
>>polytopes=clockwise(polytopes);
>>polytopes=transfer(polytopes,1,[450,1960,2800],[-30,0,0]);
>>polyface(polytopes,′E:\polytope3DEC.txt′);
(6)在3DEC中使用call命令读取MATLAB输出的文本文件。块体生成后,根据实际结构面产状重新划分滑源区块体,使用join on、jset命令生成结构面。需要注意的是,若3DEC工程坐标系与大地坐标系不同,使用jset命令时需将结构面产状参数进行相应变换。另外,考虑到计算效率,结构面间距取20im。设置边界条件、块体与接触本构参数及重力作用方向,开始力学计算。在3DEC中,滑床作为固定边界,块体采用刚体本构,接触本构为莫尔-库仑滑动模型(Itasca Consulting Group,Inc.,2016),初始平衡阶段计算参数取值见表1。
(7)达到平衡后使用geometry import命令导入dxf或stl格式的滑坡前地形,对流通铲刮区的块体进行分组,并删除位于滑坡前地形高程以上的块体,即完成流通铲刮区堆积体的建模,建立的滑坡模型如图7所示。受原始地形数据精度影响,建立的三维滑坡模型与实际原型存在一定差距。模型生成后,在3DEC中改变重力方向及接触参数,开始滑坡运动过程模拟。滑坡运动过程模拟阶段参数取值见表1。
滑体对基底物质的铲刮包括滑体前部对基底物质的铲作用与滑体对底部基底物质刮作用两种形式(Barbolini et al.,2005;陆鹏源等,2016;Sovilla et al.,2006)。滑体前部先与老滑坡堆积物接触并将其铲起(图8a),强烈的碰撞导致块体飞溅,随着运动继续发展,滑体翻越至老滑坡堆积物上部以刮的形式将其裹挟运移(图8b),类似现象同样在物理实验中观察到(陆鹏源等,2016)。图9为模拟滑坡堆积结果,模拟堆积形态呈扇形,与实际堆积形状接近。模拟出的堆积范围顺滑向水平长度约2450im,顺河向水平宽度约1240im,与滑坡实际堆积范围(顺滑向长2500im,顺河向宽1080im)较为吻合。滑体在下滑过程中受流通铲刮区西高东低地形影响,主滑方向略向东偏移,堆积厚度分布整体呈现出西低东高态势(图5)。可以看出,模拟堆积体厚度分布(图10)与实际堆积趋势一致(图2),表明采用三棱柱体能够有效地模拟出滑床的地形特征。图11为堆积区1-1′剖面堆积情况,模拟堆积厚度在中部与实际情况吻合较好,而在东、西两侧大于实际堆积厚度。该差异是由于数值模拟中采用了较小的接触摩擦角,只有极少的滑体停积滑源区与流通铲刮区,导致模拟的整体堆积厚度比实际堆积厚度略大。总体来看,模拟结果与实际具有较好的一致性。

表1 数值模拟参数取值Table 1 Parameters for the numerical analysis
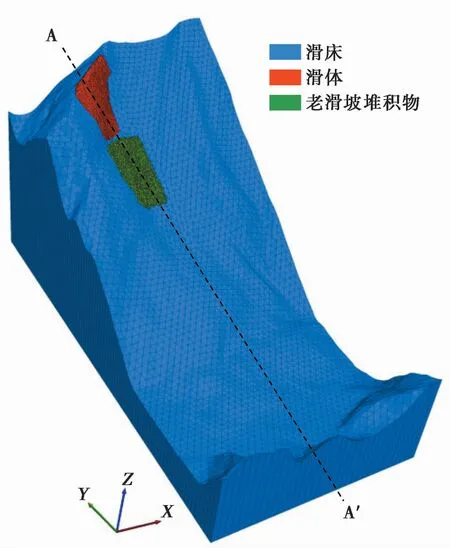
图7 3DEC滑坡模型Fig.7 Landslide model in 3DEC
4 讨论与结论
(1)本文基于MATLAB编写了复杂滑坡建模相关程序,借助滑坡前、后的地表高程数据,采用三棱柱体及Voronoi多面体对滑体、滑床和松散堆积物进行构建。此方法无须借助第三方软件进行网格划分,同时在MATLAB中完成块体生成及3DEC命令流输出,简化了建模流程。
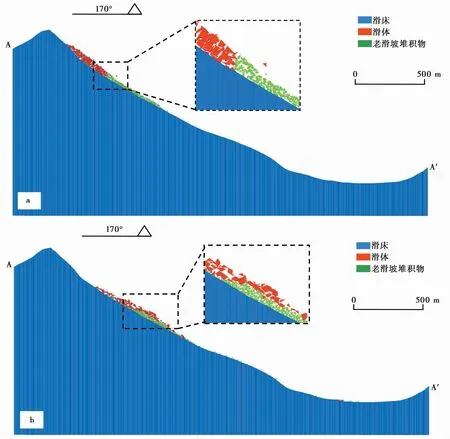
图8 滑坡运动过程中的铲刮现象Fig.8 Entrainment process of the landslide
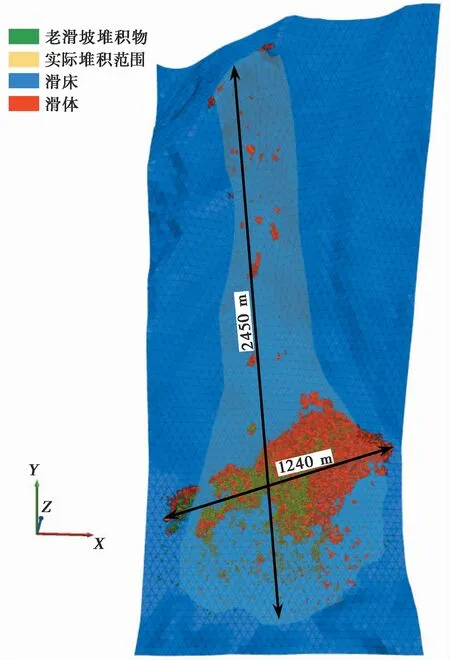
图9 模拟堆积区域Fig.9 Simulated depositional area
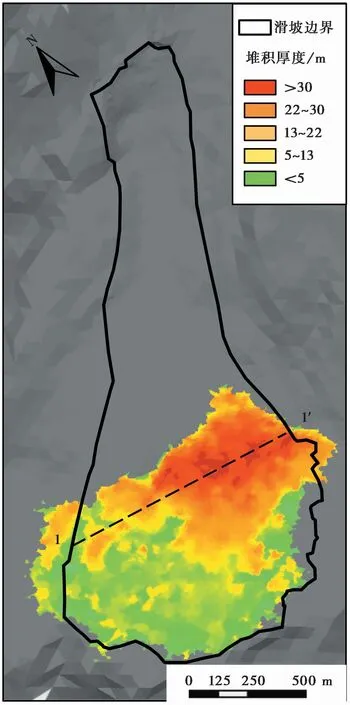
图10 模拟堆积厚度Fig.10 Simulated deposit thickness
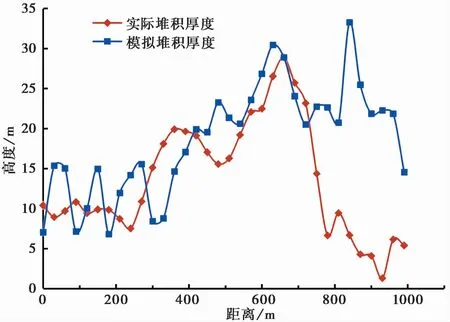
图11 “1-1′”截面模拟与实际堆积厚度Fig.11 Simulated and actual deposit thickness along“1-1′”cross section
(2)本方法是基于分区建模思路对滑坡进行建模,更适用于滑动面位置为已知的边坡,对滑动面未知的边坡而言,可考虑利用其他程序得到最危险滑面位置再进行模型的分区构建。另外,建立含结构面的滑体模型还需在3DEC中对块体进行重新分割,如何在MATLAB中实现这一功能还需进一步研究。
(3)本研究以新磨滑坡为例,详细叙述了该方法的建模步骤,并对滑坡运动过程进行反演。模拟很好地展现了滑坡过程中的滑体对沿程堆积物的铲、刮现象。同时,模拟得到的滑坡堆积形态,滑坡运动距离和滑坡堆积厚度均与实际情况表现出较好的一致性,验证了该建模方法的可行性。

