考虑变形协调的土体剪切位移分布式测试研究*
吴 涵 朱鸿鹄③ 周谷宇 施 斌 苏立君
(①南京大学地球科学与工程学院,南京210023,中国)
(②中国科学院山地灾害与地表过程重点实验室,成都610041,中国)
(③南京大学(苏州)高新技术研究院,苏州215123,中国)
0 引 言
岩土体的剪切破坏是地质工程领域较为常见的诱灾机制,常常会导致滑坡、崩塌、泥石流、地裂缝,以及各种岩土工程构件的变形和损坏,如管道屈曲、结构体开裂等,严重威胁人类的生命财产安全。对岩土体剪切变形的监测和安全评估已逐渐成为亟待解决的重要课题。传统的岩土变形监测技术以光学测量技术为主,虽然监测范围广泛,但无法获取岩土体内部实际位移。逐渐成熟的接触式电测监测技术能一定程度上弥补对岩土体内部剪切变形监测手段的缺失,但也存在传感器成活率低、耐久性和长期稳定性差、监测密度低等不足(Dunnicliff,1993)。
分布式光纤传感技术是一种以光为载体,光缆为媒介的新兴测试技术,由于其精度高、抗电磁干扰能力强,且能够实现实时、长距离的多场监测(施斌,2017;施斌等,2019),这种技术被越来越多地用于滑坡(Sun et al.,2014)、隧道(Shi et al.,2003;Klar et al.,2014)、地基基础(朱鸿鹄等,2010;雷文凯等,2018)和基坑(隋海波等,2008)等一系列工程项目。现场实施中的光缆布设方式通常分为钻孔布设法、浅表沟槽布设法和结构体布设法,可用于监测岩土体或结构体的变形稳定性(Iten,2008;柴敬等,2012;Wu et al.,2015;Suo et al.,2016;Zhu et al.,2017;Zhang et al.,2018年)。
分布式光纤感测技术应用于岩土变形监测的关键在于保证光缆本身与被测对象的变形一致性,在此基础上实现全实时、高精度的分布式监测。对于这一耦合变形问题,国内外学者均做了一些有益的探索。例如,日本工程师Sugimoto et al.(2001)开展了模型试验,使用铁板对碎石土和砂土组成的路堤模型进行剪切,分布式应变传感光缆很好地监测到了剪切面的形成演变过程。Zhang et al.(2014)通过光缆在土中的拉拔试验,分析了光缆-土体界面的力学特性,进而提出了两者变形耦合的3个阶段;李博等(2017)在土条弯曲试验中,发现在小变形时埋入式光缆和土体耦合性能较好,缆-土耦合性能可以用应变传递系数来定量描述;柴敬等(2013)发现当模型岩层下沉变形量在0~4.985mm间时,醋酸乙烯塑料封装的光纤传感器与变形的相关性高,此后灵敏度大幅下降,但仍能反映岩层的移动变形状态。在瑞士,Iten et al.(2008)和Hauswirth(2011)先后对光缆在大尺度剪切工况下的响应模式进行研究,相关结论对其工程应用有着很好的启发性。
在岩土工程实践中,通用的稳定性评价指标是位移量,因此使用分布式应变传感光缆监测岩土剪切位移时,需要在考虑变形耦合性的基础上,建立一个应变-位移的转换模型。光缆能否准确监测土体剪切的真实位移,极大程度地取决于该种转换模型的拟合程度。为了解决这一问题,SPM、LPM、logistics生长曲线等相继被提出并应用于滑坡监测数据的分析(Iten et al.,2008;李博等,2015;Zhang et al.,2018年),但这几种模型的不足在于所需参数较多,且不易确定。
本文开展了基于光频域反射(OFDR)和粒子图像测速(PIV)技术的土体剪切试验,定量分析了剪切工况下埋入式光缆的应变演化,提出了应变-位移的转化模型,并对光缆和土体之间的耦合性能提出初步的评价指标。试验结果充分验证了分布式光纤监测土体剪切变形的可行性,为该技术在岩土工程中的推广应用奠定了基础。
1 监测原理及方法
1.1 OFDR光纤监测原理
光纤中的散射光谱如图1所示,分布式光纤传感技术依据散射光受外界环境影响的特性行使其监测作用(施斌等,2019)。布里渊光时域反射(BOTDR)、布里渊光时域分析(BOTDA)等技术基于布里渊散射光原理,空间分辨率低,适用于测试距离长、精度要求不高的应变和温度监测;利用光纤中的拉曼散射光,可以建构分布式温度传感(DTS)系统;光频域反射(OFDR)、光时域反射(OTDR)均基于瑞利散射,是目前最尖端的光纤传感技术,其中OFDR与OTDR相比,具有更高的空间分辨率和信噪比。目前商用的OFDR解调仪可以在传感长度50im范围内实现1imm的空间分辨率,应变传感精度达到±1.0με,完全满足岩土剪切变形精细化监测的要求。
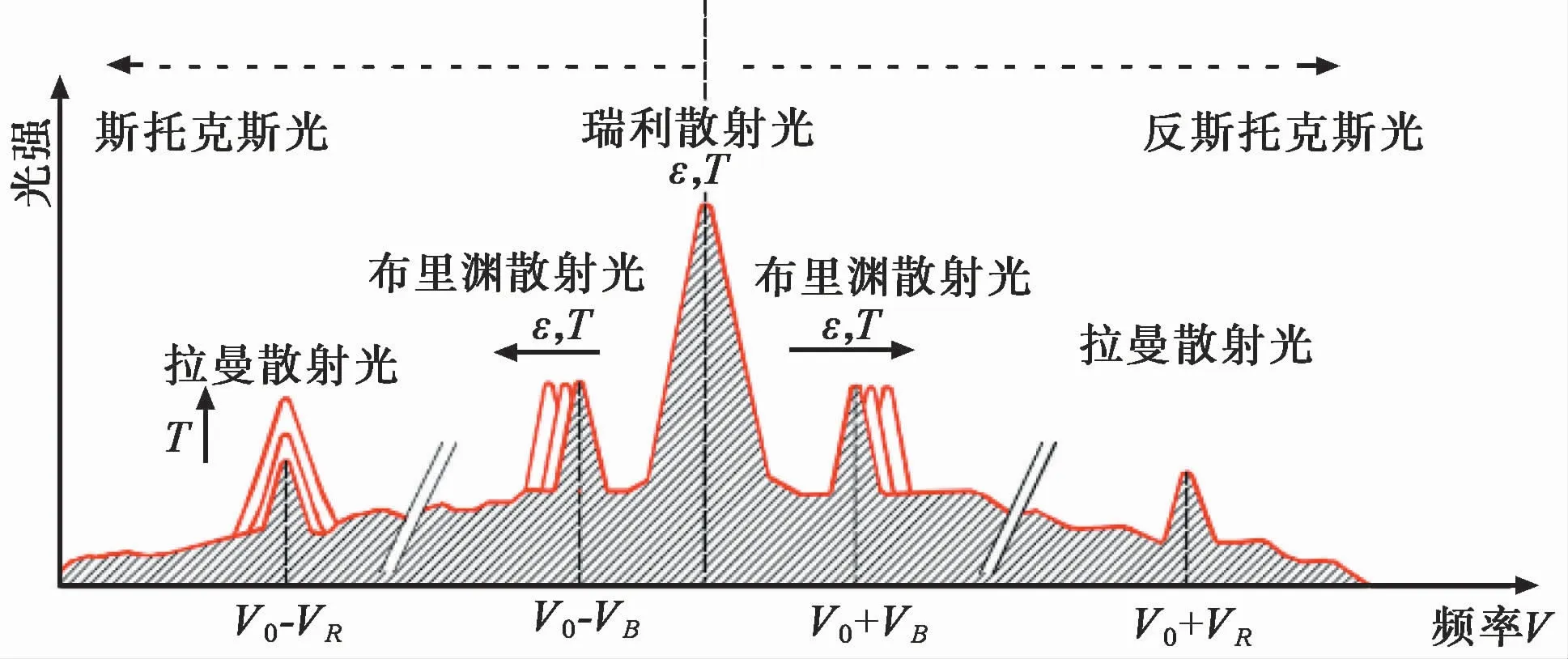
图1 光纤中的散射光谱Fig.1 Spectrum of the scattered light in an optical fiber
OFDR传感技术的基本原理是通过捕捉光纤中背向散射光与前向散射光的差异,测量光纤传输过程中由于散射、吸收等原因产生的损耗。当光纤内部某点的应变或温度发生变化时,测量到的传输损耗量与这个扰动之间存在对应关系(顾一弘等,2009),可通过下式计算得到光纤的应变量及其沿长度方向的分布情况:
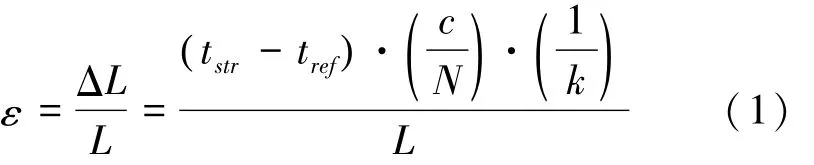
式中:ε为光纤应变;ΔL为光纤的变形量;L为光纤原长;tstr为光纤变形后的延迟时间;tref为光纤变形前的延迟时间;c为光速;N为光纤的折射率;k为应力光学校正因子,k值需在每次测试前通过预加应变来进行标定。
1.2 PIV技术监测原理
PIV是一种通过图像测量位移的摄影测量技术。其基本原理是对初始图片选取一小块搜索区域,根据其图像的灰度、纹理等特征,在后续图片中依据相关性算法进行区域的搜索并计算相关系数,并将相关系数为峰值的区域判定为变形后的区域(Stanier et al.,2015)。与传统的点式位移测量技术相比,PIV技术具有高精度、非接触、全面性等优点,只需通过图片即可获得目标的位移矢量分布。本文利用PIV技术获取土体剪切变形过程中表层剪切带的分布及其变化情况,从而与光纤监测结果进行对比验证。
1.3 应变-剪切位移计算方法
在采用分布式应变传感技术监测土体的剪切变形时,一般将封装保护过的应变传感光缆垂直于事先预估的土体剪切面埋入土体中(Zhang et al.,2018),本文据此设计了如图2所示的试验装置。通过移动位移台使得剪切试验盒内的土体发生逐级增大的剪切位移。随着土体缓慢变形,埋入式应变传感光缆也在相应地受拉变形。当光缆和土体的耦合性能良好时,两者变形一致,土体剪切位移量与光缆的应变测值之间存在着一一对应的关系,据此即可由后者反算前者。
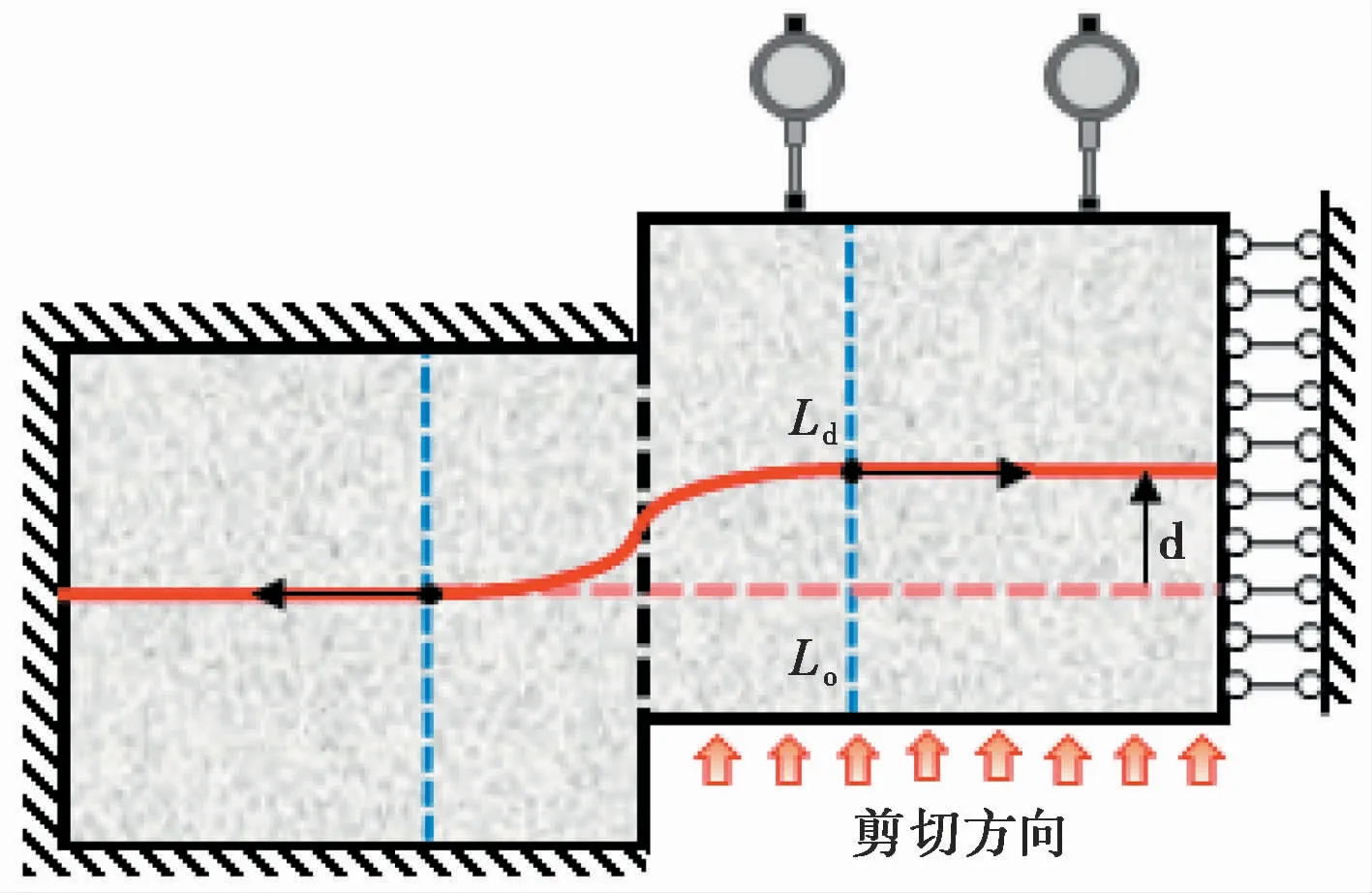
图2 土体剪切试验原理图Fig.2 Schematic diagram of the soil shear test
国内外相关的研究显示,直埋式光缆和周围土体的相互作用是一个非常复杂的问题,光缆的应变测值和真实的土体变形之间有着一定的应变损失,且影响因素众多,因此至今没有很好的从应变换算剪切位移的解决方案(Iten et al.,2008;李博等,2015;Zhang et al.,2018)。本文借鉴了地面沉降监测中的应变积分法思路(吴静红等,2017;施斌等,2018),通过计算光缆所测应变沿其长度方向的积分值(在小变形的假设下,该值即光缆的轴向伸长量)来推算土体的剪切位移,两者之间的比值记作缆-土剪切耦合变形系数,为一无量纲数,其表达式为:
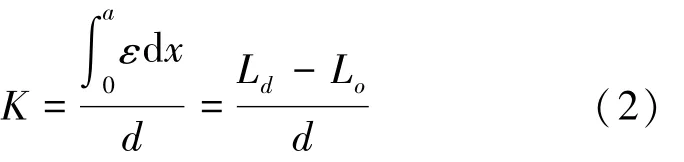
式中:d为土体发生的剪切位移;ε为沿光缆伸长方向上的应变值,为与x有关的函数;a为应变积分的上限,及剪切变形影响区的边界;Lo和Ld分别为土体变形前、后的光缆长度。缆-土剪切耦合变形系数K实际表征的是光缆伸长量随土体剪切位移发展而增大的斜率,可通过室内标定试验确定。需要指出的是,当缆-土变形开始不协调(即发生滑脱时)时,K值迅速下降,此时根据光缆应变读数无法准确计算土体的剪切位移。这一时刻的剪切位移限值为ds,光缆的应变积分值即为缆-土界面的滑脱位移限值ΔLs。
在应用上述应变积分法间接计算土体的剪切位移时,要注意K、ds和ΔLs的取值受到多种因素的影响,如光缆的直径和材料、是否设置锚固点,土的粒径级配、含水率和压实度,上覆压力等。以下通过室内剪切试验对此问题进行定量分析。
2 室内剪切试验
2.1 试验设置
室内剪切试验设置如图3a所示。剪切盒长50icm、宽25icm、高20icm,对称分为左右盒,左盒底部较右盒高,以螺钉固定于试验台上;右盒底部设置滚珠滑轨,用位移台逐级缓慢推动右盒,使盒内的土体发生错动剪切,右盒背部安装两个百分表以测量实际剪切位移。盒内土体高度为17icm,在填土时分层布设应变传感光缆(图3b)。光缆共分3层(z=5icm、10im、15icm,从低到高分别标记L、M、H层),除L-1段外其他光缆均为光滑光缆,L-1的光缆段均匀设置4个热缩管式锚固点(图3b、图3c)。所用热缩管外层为柔软辐照交联聚烯烃材质、内层为热熔胶材质,取出其内置的增强不锈钢棒后截断为长约30imm、直径1.5imm的透明塑管,串联在光缆护套外部x=10imm、20imm、30imm、40imm处,并采用光纤熔接机充分加热使其颈缩,形成一个整体。该处理措施可保证热缩管与光缆间不会出现早于缆-土间的滑脱作用。剪切盒上方安装佳能600D数码相机,试验过程中连续拍照,用于PIV变形分析。每级位移台推动后,采用武汉隽龙科技有限公司出产的OSI-S型OFDR解调设备采集光缆的应变读数,空间分辨率设置为10imm。
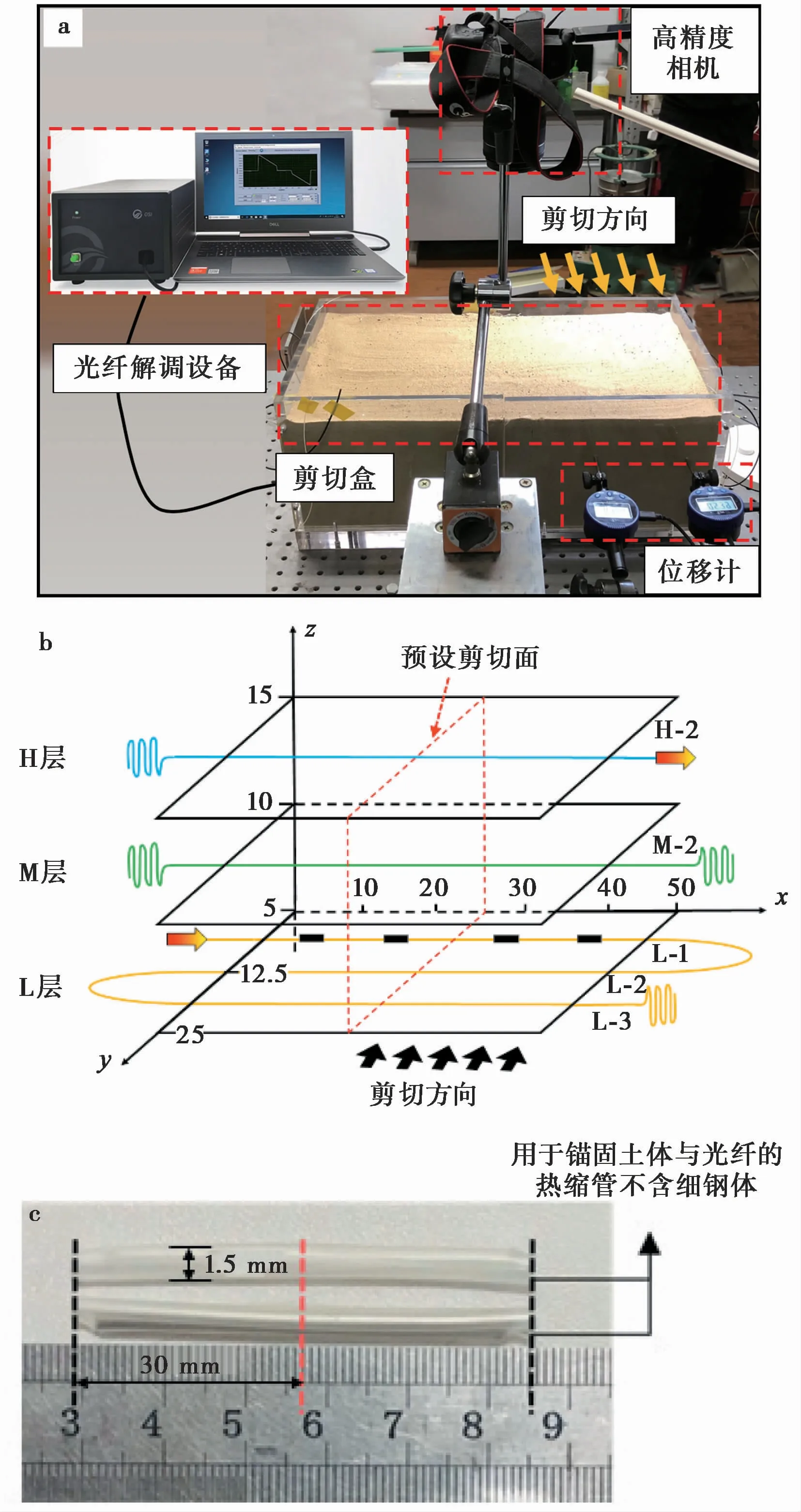
图3 土体剪切试验设置图Fig.3 Setup of the soil shear test
2.2 试验材料
剪切试验用土取自南京市栖霞区长江边的砂土,晒干后过孔径为2imm的筛备用,其基本物理指标及颗粒级配曲线分别见表1及图4。根据土的工程分类标准(GB/T 50145-2007),试验用砂为级配不良的粗砂。试验中所用光缆为0.9imm外径的紧套式应变传感光缆,护套材料为白色PVC,内部为G652(B)型单模光纤,由苏州南智传感科技有限公司生产。

表1 试验用土的基本物理参数Table 1 Physical parameters of the test soil
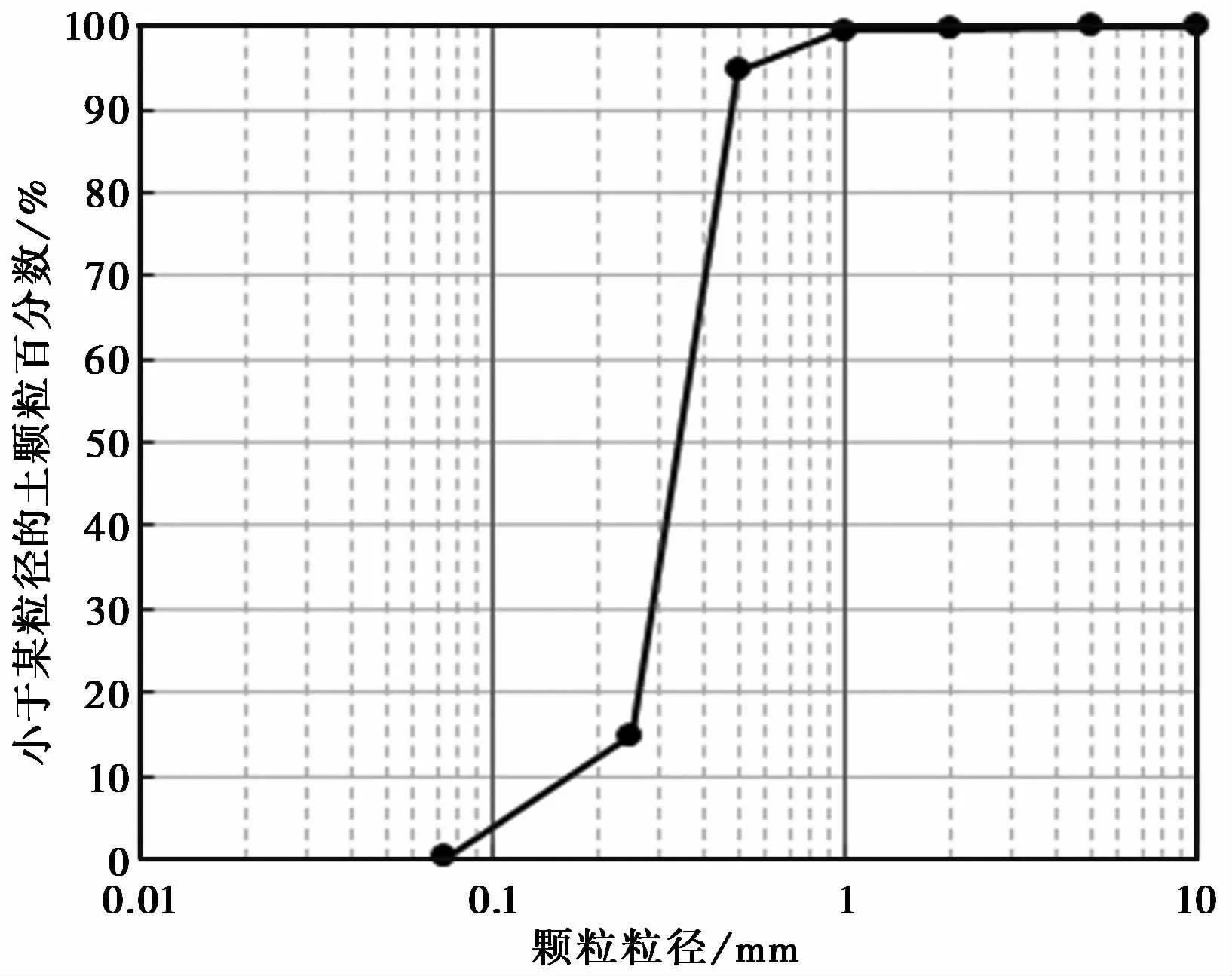
图4 试验用土的颗粒级配曲线Fig.4 Grain size distribution curve of the test soil
3 试验结果分析
在土体剪切试验中,位移台施加的最大剪切位移为23imm。由于试验历时较短,室内温差约为1i℃,忽略了温度变化对OFDR读数的影响。图5为实测沿y轴负方向剪切位移分别为5imm、10imm、15imm和20imm时的各段光缆应变分布。
图5显示,3层分布式应变传感光缆在剪切试验中均灵敏地监测到了其布设位置的土体剪切变形。对比各光缆段的应变分布可以看出:
(1)由图5b、图5d和图5e可知,光缆由于埋设深度的差异,上覆压力略有不同,光缆应变测值也呈现出不同的分布形状和峰值。具体表现为,上覆压力越大,应变越集中,应变峰值也越大,各层间应变峰值相差数倍,这与边坡试验的滑动带附近应变分布规律一致(Song et al.,2017;Yan et al.,2017)。这是因为在较大围压的作用下,光缆和土体的变形耦合性得以增强,两者之间的应变传递率较大。
(2)对比图5a~图5c可知,设置有锚固点的光缆相较于光滑光缆应变峰值要大很多。对于包含锚固点的光缆,应变分布有明显“分段增长”的现象,与之前光缆在土中拉拔试验的结果类似(Zhang et al.,2014),且增长速率较为均匀。而对于光滑光缆,应变沿光缆长度的分布更为平滑,在剪切后期应变不再持续增长,甚至开始下降。这是因为光缆在管式锚固的作用下,与土体的耦合性得到极大的提升,其监测到的土体应变也要增长数倍,而光滑光缆在土体发生大变形后逐渐与周围土体发生了滑脱。
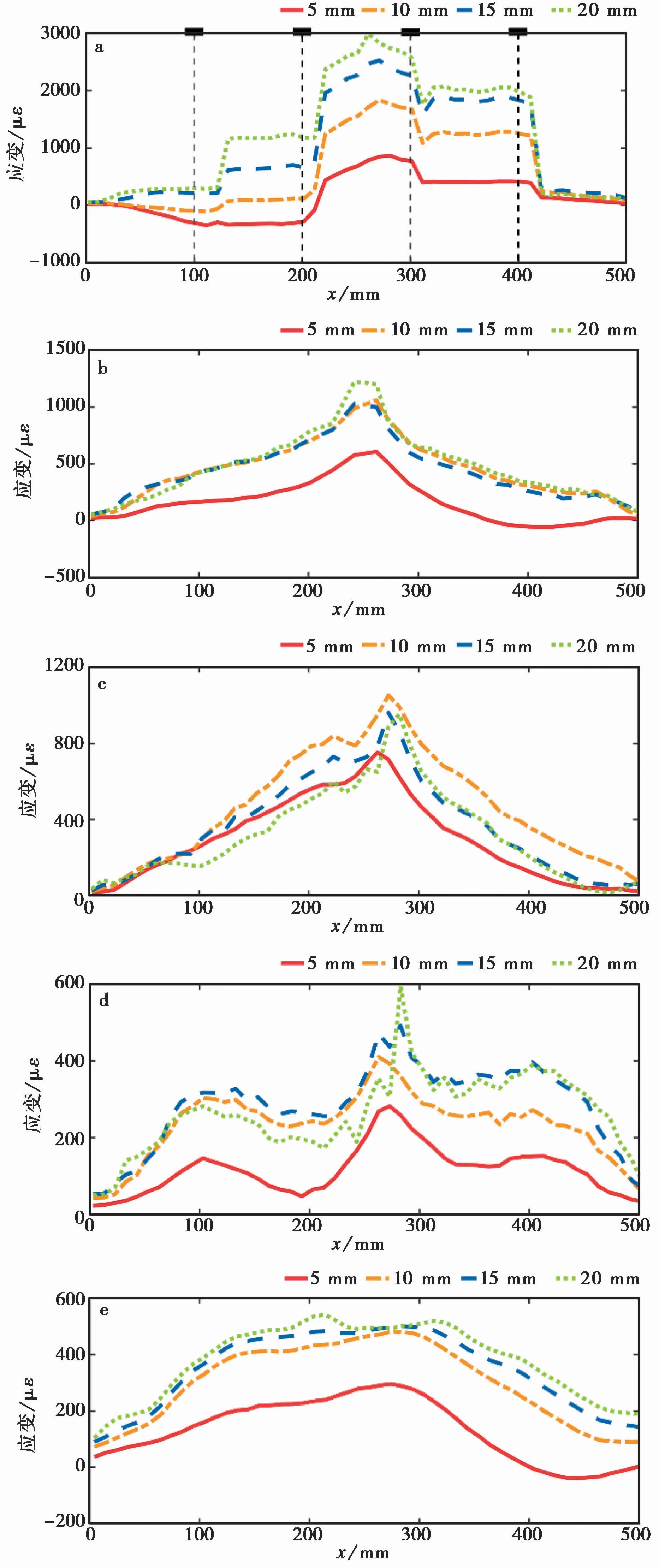
图5 不同剪切位移情况下的各光缆应变分布图Fig.5 Strain distribution data of the optical fiber cables under different shear displacements
由前述可知,随着土体剪切位移的增大,光缆被拉长,其伸长量(即图5中应变分布曲线与x=0直线之间相夹的面积)也相应增大。依据式(2),绘制光缆伸长量(Ld-Lo)与土体剪切位移d之间的关系曲线(图6)。结果显示,该关系曲线的初始段可以用线性拟合,在图中用虚线表示。拟合参数列于表2内。
根据图6及表2可以看出:
(1)在土体发生逐级增大的剪切位移时,根据光缆与土体的耦合状态,可分为缆-土良好耦合阶段和缆-土滑脱阶段,分别对应图6b~图6e中的Ⅰ阶段和Ⅱ阶段。其中Ⅰ阶段光缆与土体耦合良好、变形协调,光缆的伸长量和土体剪切位移基本呈线性增长,图中虚线为采用MATLAB线性拟合的结果;Ⅱ阶段光缆与土体发生滑脱,此时光缆应变分布受到多种因素的影响,光缆应变不能很好地反映真实的土体变形。
(2)表2中为缆-土良好耦合阶段的拟合结果。缆-土剪切耦合变形系数K值的大小可以反映光缆护套与土体间相互作用的效应。对比图5及图6b~图6e可知,K值的大小可以用于判断各光缆段缆-土耦合性的好坏。K值越大,光缆与土体的耦合性能越高,光缆能够监测到的应变也就越多。其中,K值最大的是L-1锚固段光缆,光滑光缆普遍比该段光缆K值偏小;M-2和H-2层光滑光缆的K值较L层小,是由于上覆土压力减小,缆-土耦合性能变差,这与光缆应变分布图得到的结果互相印证。
(3)缆-土滑脱伸长量ΔLs为光缆与土体间仍能保持耦合的最大光缆伸长量,当Ld-Lo=ΔLs时,两者界面开始出现滑脱。因此,ΔLs在一定程度上也可以反映光缆和土体间的耦合特性。对比图5及图6b、图6c可知,同层间L-3段光缆的K值、缆-土滑脱伸长量ΔLs均大于L-2段光缆,这是因为L-3段光缆更靠近位移控制的推动装置,侧向压力更大,其耦合性得到了加强。
(4)对比图6b~图6d及表2可知,K值越大,光缆就容易更早地达到其滑脱伸长量,因此对应的缆-土滑脱位移就相对越小。同时对比图5a数据发现,锚固段的K、ds值都很大,这说明当使用热缩管锚固光缆和土体时,在锚固作用下,光缆和土体间的摩擦增大,不仅光缆和土体的耦合性能得到较大的提高,而且在整个变形过程中这种耦合性得到了很好地保持。
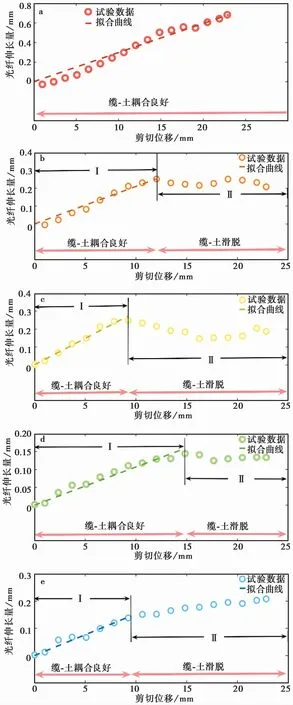
图6 光缆应变积分值随剪切位移的变化曲线Fig.6 Relationship between strain integral value and shear displacement
(5)对比图6b~图6dⅡ阶段图像,光缆与土体滑脱之后,伸长量随土体位移增加而下降,可能与光缆材料的弹塑性有关,出现小部分弹性应变恢复的现象。
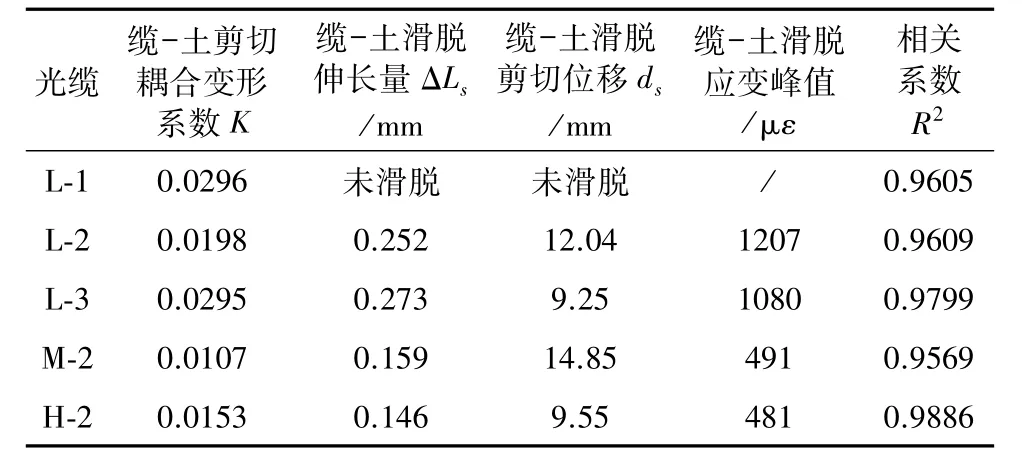
表2 应变积分法拟合结果Table 2 Fitting results of the strain integral method
(6)由图6可知,光滑光缆达到其滑脱伸长量后会与土体发生相对滑移,此时随着土体剪切位移的增大,光缆的伸长量反而略有减少。而图6e中Ⅱ阶段虽然斜率有明显减小,光缆的总伸长量却仍在上升,且H-2光缆Ⅰ阶段的斜率值比M-2光缆要大。这是由于图6e中H层光缆接近土体表层,上覆压力很小,光缆变形不再是传统直剪试验中的平面应力问题,而是转变为三维变形问题,剪切过程中观测到土体出现较为明显的隆起和剪胀现象,因而H层光缆很早就出现部分滑脱的现象,但在滑脱后光缆由于土体的三维变形而持续伸长。
本次试验研究综合考虑了围压、管状锚固等因素对缆-土剪切耦合效应的影响,虽然只进行了一组试验,但在试验中同时布设了5条不同工况的光缆,系统分析了多种缆-土耦合条件下的剪切变形监测数据,据此提出缆-土剪切耦合变形系数,并用于定量评价剪切过程中光缆和土体之间的耦合程度。参考钻孔回填料与应变光缆耦合性评价方法(张诚成等,2018),对于和本文研究工况类似的情况,建议采用表3所示的缆-土剪切耦合性划分标准。
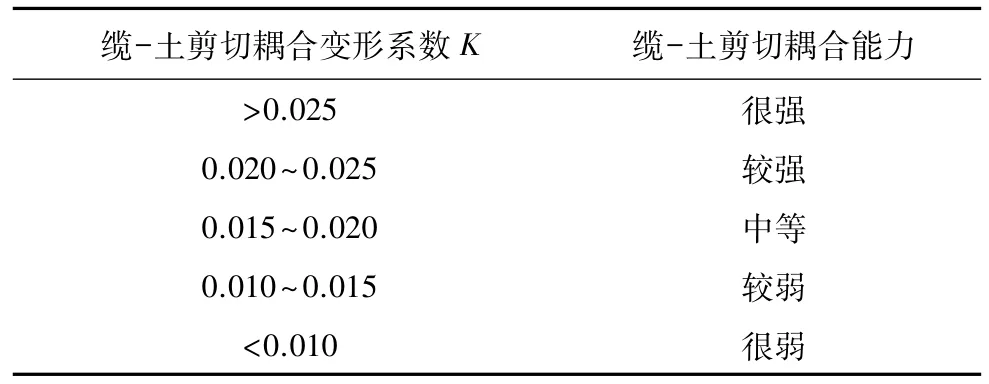
表3 本研究中缆-土剪切耦合性划分建议Table 3 Recommendation on classification of OF-soil coupling in this study
4 讨 论
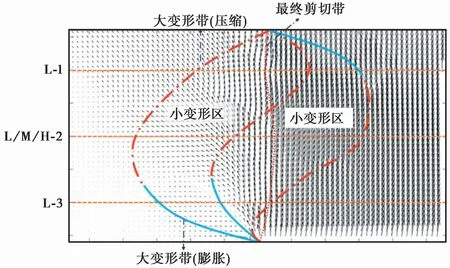
图7 PIV分析得到的土表层位移矢量图Fig.7 Calculated vectorial displacements of soil surface using PIV analysis
通过PIV图像处理技术对剪切试验全程照片进行处理,可得到表层土体变形的位移矢量图,同时可大致确定其剪切带分布情况(李元海等,2007)(图7)。图中水平虚线为光缆布设位置。
(1)图5a、图5b、图5e段中的应变分布均出现了负应变区。由图7可知,土颗粒在剪切过程中并不全部都沿剪切方向运动,剪切盒固定端部分土颗粒发生了转向甚至旋转,在土体变形较小时,光缆与土体耦合性较好,光缆随土体发生了收缩,产生了负应变区。
(2)如图3c所示,试验过程中所使用的锚固方式为热缩管式锚固,热缩管具有外层材料绝缘防蚀,内层熔点低、黏接性好的特点,加热使其颈缩以提高光滑光缆和土体的耦合变形性能。与瑞士ETH大学Iten等开展的剪切试验(Iten et al.,2009)中使用的十字光缆夹具相比,热缩管锚固体积更小,因此对土体变形几乎没有扰动,能够监测到更加真实的土体变形情况。
(3)光缆应变积分法的优势在于,当保证缆-土耦合变形时,只需采用简便的、只含有一个参数的线性模型即可进行剪切位移的推测;缆-土剪切耦合变形系数K的确定可通过开展不同工况、不同种类的光缆和土体的室内或现场试验得到。
5 结 论
本文通过剪切试验研究了埋入式光缆应变与周围土体的剪切变形之间的关系,采用简便的应变积分法将应变测值转换为土体的剪切位移,主要结论如下:
(1)通过土体剪切试验,获得了剪切过程中光缆的分布式应变测值,验证了全分布式OFDR技术在监测土体剪切变形的可行性和准确性。
(2)对于本次试验的工况,当土体剪切位移较小时(小于9~15imm),光纤与土体耦合性能良好,光缆应变能很好地反映土体的变形情况,有无锚固对于光缆监测土体变形影响不大;当土体变形增大到一定程度(15imm以上),光缆与土体发生滑脱,此时光缆伸长量随位移的增大而趋于固定值甚至减小,难以真实反映土体的剪切变形。
(3)在缆-土良好耦合阶段,光缆伸长量计算值与土体剪切位移之间存在着线性关系,缆-土剪切耦合变形系数K及光缆轴向伸长量ΔLs均可以一定程度上表征光缆和土体的耦合程度。对于同种光滑光缆,K值越大,发生滑脱时的土体位移ds越小。
(4)依据本文提出的缆-土剪切耦合性划分建议,在光缆上以10icm间距均匀安装管式锚固点时,可以将缆-土剪切耦合变形系数提高至0.025以上,耦合能力很强;提高围压也能达到同等效果。
需要指出的是,本文仅仅开展了初步的土体剪切位移监测可行性的试验研究,实际岩土工程实践中发生的剪切变形要复杂得多。为了实现更高精度的监测效果,下一步需要更加深入地研究不同的锚固类型及围压状态下光缆与土体的耦合性差异,建立理论上更加科学、合理的光缆应变-土体剪切位移转换模型。

