财政分权与市场整合对工业用地利用效率影响的异质性研究

朱于珂，黄 毅

（1.中南财经政法大学 经济学院，武汉 430073；2.湖南工程学院 管理学院，湖南 湘潭 411104）

工业用地是工业发展的载体，工业用地利用效率不仅在一定程度上会影响未来工业发展的弹性与空间，且对区域生态环境影响巨大。在全面建成小康的决胜阶段，城镇化、工业化加速发展，必须合理有效地提高工业用地利用效率，促进工业用地集约化，推动经济持续稳步增长。在供给侧结构性改革的背景下，提升工业用地利用效率对推动工业转型升级、促进工业经济由规模速度型向质量效益型转变、加快发展生态工业意义重大。2016 年7 月，中华人民共和国工业和信息化部发布的《工业绿色发展规划（2016—2020 年）》明确指出：“工业领域坚持把发展资源节约型、环境友好型工业作为转型升级的重要着力点”，而提高工业用地利用效率正是促进工业绿色发展的重要环节。

财政分权关乎各地区政府的经济自主权，作为经济分权的重要组成部分，财政分权对工业用地利用效率乃至工业发展的作用不言而喻。与此同时，财政分权背景下，各地政府自主决策度加强，市场一体化建设步伐加速。市场整合直接影响区域技术创新与经济发展［1］，而工业用地效率受区域经济发展的影响显著［2］，因此，市场整合必然会对区域工业用地利用效率产生影响。然而，在工业用地利用效率不同的地区，财政分权与市场整合对工业用地利用效率的影响程度必然不同。本文的主要贡献在于：构建面板分位数回归模型，创新性地探索了在不同分位数水平上财政分权与市场整合对工业用地利用效率及其增长率的异质影响；对工业用地利用效率影响机制进行更加系统全面的研究；针对本文得出的研究结论，因地制宜，为提高工业用地效率提出有效的政策建议。

一、文献回顾

（一）财政分权对工业用地利用效率的影响机制分析

目前，国内外已有许多学者探索了地方政府竞争对工业用地利用效率的影响机制。罗能生和彭郁［3］认为，政府竞争会直接影响工业资本从而影响工业用地利用效率，通过实证得出，政府竞争对促进工业用地利用效率效果显著。财政分权代表一个政府的财政自主度，是政府竞争的重要体现。财政分权程度越高，地方政府发展本地经济的财政激励越强。财政分权很大程度上影响了各级政府乃至不同地区的财政支出效率与结构［4］。陶然等［5］认为：财政分权在经济发展水平较低的地区可能会导致政府间开展低水平竞争，从而阻碍技术进步，降低生产要素的利用效率。同时由于财政自主度较高，地区间为争夺流动性税基而开展的“土地引资竞争”就越激烈，工业地价扭曲，导致工业用地不合理扩张，工业用地利用效率损失也越严重。因而有学者认为财政分权会对工业用地利用效率产生负面影响［6］。但也有学者存在不同的观点，例如，姜海和曲福田［7］认为：财政分权有利于政府通过促进当地科技进步，从而提高工业用地利用效率；严思齐和彭建超［2］通过门槛回归分析得出，在不同经济发展程度地区，财政分权对工业用地利用效率具有差异化影响：在经济发展发展水平较低的地区，财政分权对工业用地利用效率具有显著负向影响；但是在经济发展水平较高的地区，财政分权对工业用地利用效率具有显著正向影响。然而，上述研究忽略了在工业用地利用效率不同的地区，地方政府根据实际情况与不同发展水平的动态变化，财政分权或者政府竞争对工业用地利用效率的影响必然会存在差异。因此，财政分权对工业用地利用效率的影响机理需要进行更系统、更全面的动态化研究。

（二）市场整合对工业用地利用效率的影响机制分析

市场整合，通常也被称为市场一体化，是指在地理空间中分散的两个或两个以上独立市场通过某种方法组成单个的统一市场，是指各区域、各产业之间产品和生产要素自由流动、规则一致，最终表现为价格合理、资源配置的高效利用。张友国［8］认为，市场一体化指的是各地区商品和生产要素在市场机制的作用下，按照市场规律在各地区间流动。市场整合直接影响区域技术创新与经济发展［1］，一方面市场整合有利促进规模经济的出现，并提高生产力［9］；另一方面市场整合在加速区域竞争的同时，也刺激了科学技术更新与传播［10］。由于工业用地效率受区域经济发展与科技水平的影响显著［2］，所以市场整合必然会对工业用地利用效率产生影响。目前，市场整合是市场化改革的重要举措。有学者从实证的角度上，研究了市场化改革对土地利用效率的影响，例如，Du 等［11］通过实证研究，发现城市土地市场化改革对土地利用效率具有正向影响；赵爱栋等［12］通过研究发现，在中西部地区，工业用地市场化改革显著地促进了工业用地利用效率的提高；而在东部地区，工业用地市场化改革却对工业用地利用效率产生了负向影响。然而由于市场化改革的概念太过宽泛，市场化改革对工业用地利用效率的影响研究大多停留在宏观层面，鲜有学者对市场整合与工业用地利用效率之间的动态关系进行深入研究。

综上，财政分权与市场整合对工业用地利用效率的影响机制如图1 所示。目前大多数学者在研究财政分权对工业用地利用效率的影响时，仅考虑了两者之间的单一线性关系；目前关于财政分权与市场整合对工业用地利用效率的影响还没有一个统一的定论；此外，大多数学者对于市场化改革与工业用地利用效率之间关系的研究仅停留在宏观层面，将市场化改革这一概念细化，并集中研究市场整合对工业用地利用效率影响的文献较少，更是鲜有研究考虑到财政分权与市场整合对工业用地利用效率的共同作用与影响；在工业用地利用效率不同的地区，财政分权与市场整合对工业用地利用效率的影响是否会存在异质性？因此，本文构建面板分位数回归模型，分析在不同分位数水平上财政分权与市场整合对工业用地利用效率的影响差异，对工业用地利用效率影响机制进行更加系统、全面的动态化研究。

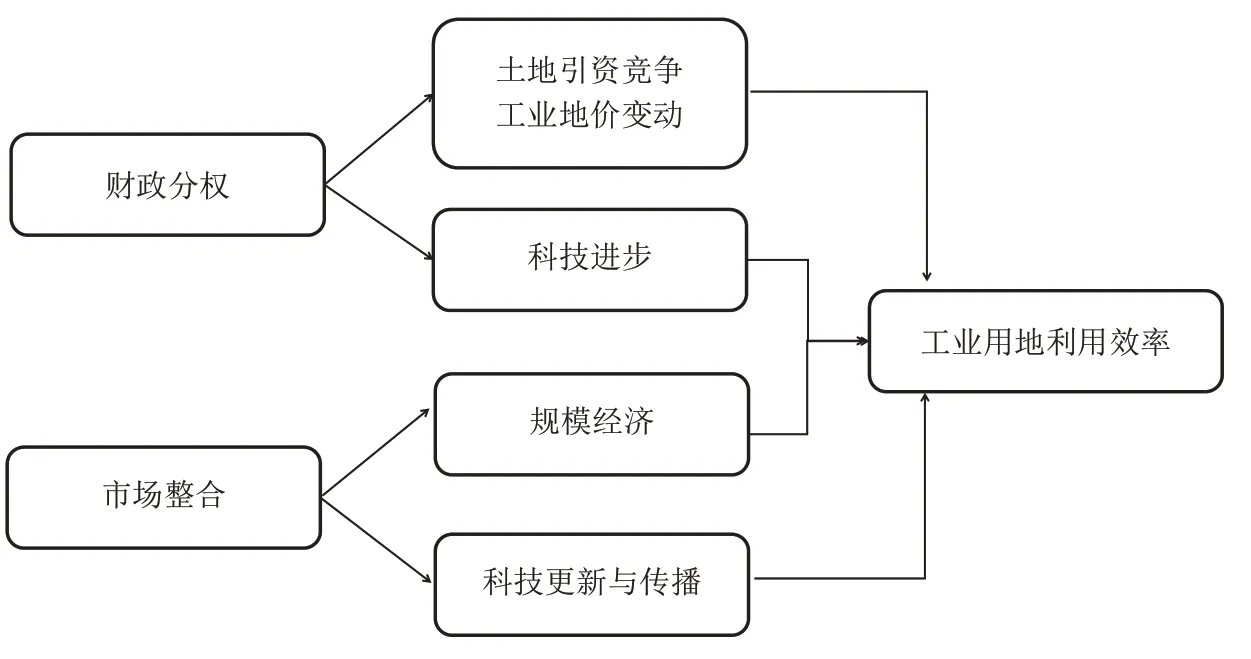
图1 财政分权、市场整合对工业用地利用效率的影响机制

二、研究方法

（一）市场整合的测度

关于市场整合的测度，本文参考桂琦寒等［13］的方法——相对价格法进行测度。在该方法中，市场整合划分为消除了地理距离因素的市场整合与未消除地理距离因素的市场整合。

本文利用一个3 维（t×m×k）的面板数据来计算市场中各类商品的价格方差。三维数据中，t代表时间，m代表地区，k代表商品。在时间上，选取2005—2017 年期间的数据；在地区上，选取除西藏、海南、重庆与港澳台地区外的28 个省份进行研究；在商品种类上，选取文化体育用品、服装鞋帽、鲜菜、书报杂志、粮食、中西药品、燃料、日用品以及饮料烟酒这9 类商品的零售价格指数。测算市场整合的数据来源于历年的《中国统计年鉴》，其中时间t为13 年，地区m为28 个，商品k为9 类，由此可以构建一个所需要的13×28×9 三维面板数据。

然后，本文将时间t与地区i、j固定，从而可以计算出t×m×（m-1）/2 个9 类商品之间价格变动的平均值的方差通过对这些方差的对数进行差分，可以得出本文需要的相对价格，即根据对数函数的性质，可以进一步用式（1）来计算

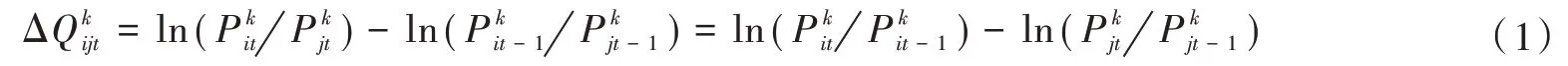
作为分割的对应指标，可以用式（3）来定义各省市的市场整合程度（MIntit）：

（二）财政分权与工业用地利用效率测度

关于财政分权的测度，本文参考严思齐和彭建超［2］的方法，使用“财政自主度型”指标来进行测度，该指标分母与分子均存在跨地区以及跨时期变化，更加适用于面板数据。具体如下：

其中：fdit表示i省份第t年的财政分权程度；frit与feit分别代表i省份第t年省本级预算内财政收入与财政支出。财政分权程度越大，表示该地区财政自主程度越高。

DEA 模型可以用于测算各行业效率值，目前已被国内外学者广泛使用［14］。关于工业用地利用效率的测度，由于先前大部分学者在研究工业用地利用效率时，未考虑到环境约束，即没有考虑对环境带来负向影响的非期望产出变量［15］，因此，本文采用SBM-DEA 模型进行测度，计算出考虑环境约束的工业用地利用效率。本文将各省的工业企业年平均从业人员数量、工业企业固定资产净值余额以及工业用地面积作为工业用地生产过程中的劳动力、资本以及土地的具体投入变量，以各省份第二产业增加值作为期望产出变量，以各省份一般工业固体废物产生量作为非期望产出，具体如下：

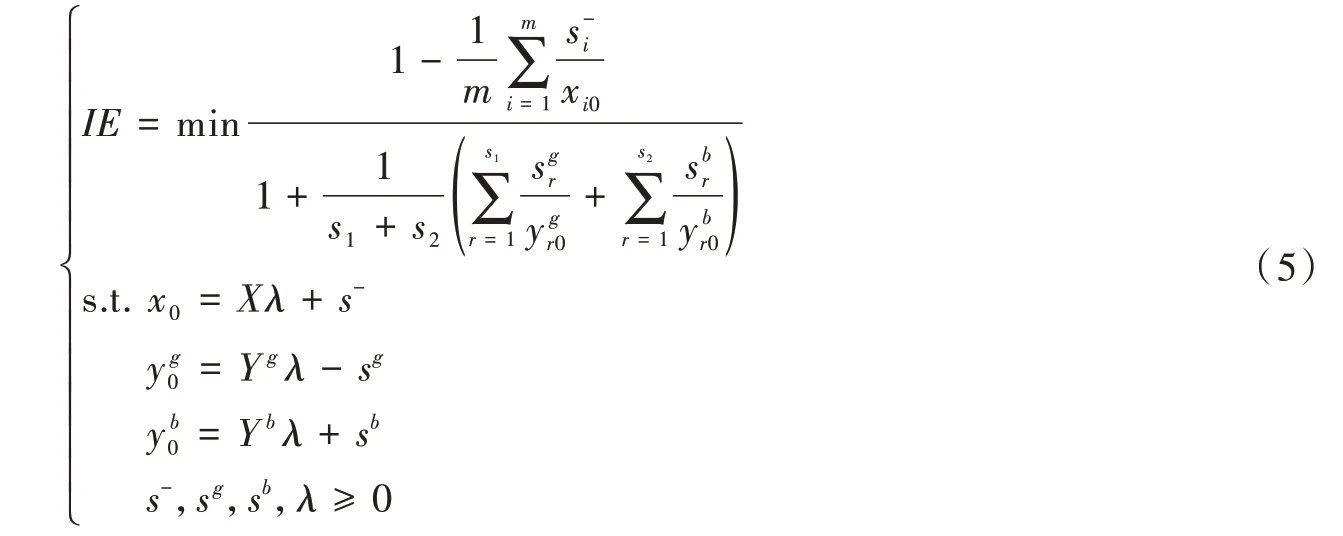
其中：IE是指工业用地利用效率；X代表投入，具体指生产过程中所投入的劳动力、资本以及土地，在本文分别以从业人员数量、工业企业固定资产净值余额以及工业用地面积指代；Yg与Yb分别表示期望产出与非期望产出，具体用第二产业增加值以及一般工业固体废物生产量指代；λj是第j个DMU 的权重，s-、sg、sb分别代表投入、期望产出与非期望产出的松弛变量。当各松弛变量都为0 时，IE=1，此时决策单元有效。

（三）面板分位数回归模型

本文构建具有固定效应的面板分位数回归模型，研究财政分权与市场整合对工业用地利用效率的影响。研究财政分权与市场整合对工业用地利用效率的影响，对于帮助政府政策制定者制定提高工业用地利用效率的政策具有重要意义。分位数回归在不同分位点水平，均可得到不同分位数函数。在先前的研究中，绝大多数学者仅采用了均值回归来财政分权与市场整合对工业用地利用效率的影响，然而传统的均值回归可能会遗漏掉一些重要信息［16］，使得回归系数的估计结果不准确，甚至无法检测到变量之间的真实关系［17］。相对于OLS 方法，分位数回归可以研究各影响因素所带来的异质性影响［18］，且分位数回归更加稳健［19-20］。分位数回归方法结合应用了回归分析与条件分位数，可应用于估计解释变量X与被解释变量Y分位数之间的关系，并反映解释变量在不同分位数水平上对被解释变量的影响差异［21-23］。构建固定效应的面板分位数回归模型可以深入探究财政分权与市场整合对工业用地利用效率的异质效应，从而帮助政策制定者因地制宜，制定更加科学合理的政策。为了将分位数回归应用于面板数据，许多学者［24-27］集中对相关的计量经济学理论进行了研究。具有固定效应的面板分位数回归模型具体如下：

固定效应面板分位数回归的主要问题在于它包含有大量的固定效应（αi），且易受到附带参数的影响［28］。当个体数量增加到无穷大时，估计量是不一致的，而每个横截面的观测量是固定的。在分位数回归中，使用标准方法去除未观察到的固定效应是不可行的。因为这取决于这样一个事实：期望是线性算子，条件分位数不能满足这一要求［27］。为了解决这一问题，Koenker［24］提出了“收缩法”。在最小化中引入惩罚项来解决估计大量参数的计算问题是这种方法的独特之处。参数估计具体如下：

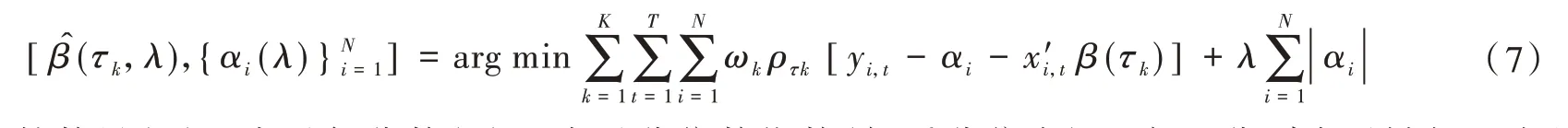
其中：i表示省份数量（N）；t表示年分数（T）；k表示分位数指数（如kth分位点）；yit与xit分别表示被解释变量与解释变量；ρτk表示估计量的损失函数；ωk表示kth分位点对应的权重，本文使用加权分位数，令ωk=1/k［29］；λ是调谐参数（tuning parameter），它可以将个体效应降低到0，从而提高系数估计的准确度。如果惩罚项的系数λ为0，惩罚项就消失了，我们便可以得到通常的固定效应估计量；如果λ趋于无穷大，我们将得到一个没有个体效应的估计结果。本文参考Damette 和Delacote［30］，设定λ=1。

根据工业用地利用效率影响机制分析，构建相应的面板分位数回归模型，研究财政分权与市场整合在不同分位点上对工业用地利用效率的影响差异，具体模型如下。分别表示i省份第t年的工业用地利用效率以及工业用地利用效率增长率；fdit表示i省份第t年的财政分权程度

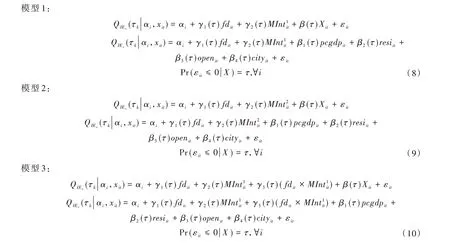
其中：被解释变量为IEit与分别代表i省份第t年消除了地理距离因素的市场整合与未消除地理距离因素的市场整合表示财政分权与市场整合的交互项；Xit表示各个地区不同年份的控制变量，模型1～模型8 中控制变量包括：经济发展水平（pcgdpit）、外资投入（openit）、科研投入水平（resiit）以及城市化水平（cityit）；τ是各分位数，本文对工业用地利用效率由低到高的10th、20th、30th、40th、50th、60th、70th、80th以及90th（10%、20%、30%、…、90%）这9 个分位数上进行回归分析，而γ(τ)是指τ分位数上影响工业用地利用效率的回归系数。

三、变量选取与数据说明

根据前文的工业用地影响机制分析，本文选取被解释变量、核心解释变量以及控制变量如下。

（1）被解释变量。本文通过构建SBM-DEA 模型，测算出中30 个省份（西藏与港澳台地区因数据缺失而剔除）2005—2017 年间工业用地利用效率IEit，以此为模型1～模型4 的被解释变量，具体见表1。同时计算出30个省份2006—2017 年间工业用地利用效率增长率，以此为模型5～模型8 的被解释变量。

（2）核心解释变量。本文选取的核心解释变量为财政分权程度（fdit）；市场整合程度，包括除去了地理距离因素的市场整合与未除去地理距离因素的市场整合；财政分权与市场整合的交叉项（fdit×

（3）控制变量。根据先前学者关于工业用地利用效率影响因素的研究，本文选取地方经济发展水平（pcgdpit）、外资投入（openit）、科研投入水平（resiit）以及城市化水平（cityit）为控制变量。地方经济发展水平采用各省份人均GDP 进行表示（以2005 年价为基准）；外资投入采用各省份外商固定资产投入比上各省份GDP；科研投入水平采用各省份科研固定资产投入比上各省份GDP；城市化水平采用城市化率衡量，即城镇人口比重。

以上数据中，被解释变量工业用地利用效率IEit、核心解释变量财政分权程度（fdit）以及市场整合程度MIntit（市场整合程度MIntit缺乏重庆、海南、西藏与港澳台地区的数据）所需的计算数据均来自《中国工业统计年鉴2006—2018》《中国城市统计年鉴2006—2018》以及《中国统计年鉴2006—2018》；其余控制变量数据均来自《中国统计年鉴2006—2018》。

四、实证结果分析

（一）工业用地利用效率测算结果

通过SBM-DEA 模型，可测算出中国30 省份（除西藏以及港澳台地区）2005—2017 年工业工业用地利用效率，具体见表1。本文根据各省份2005—2017 年平均工业用地利用效率绘制成图2，以便对各省份平均工业用地利用效率进行区域对比分析。为了更加直观地观察各省份在2005—2017 年间工业用地利用效率的变化趋势，本文根据2005—2017 年间各省份每年的工业用地利用效率值，绘制成折线图，如图3 所示。

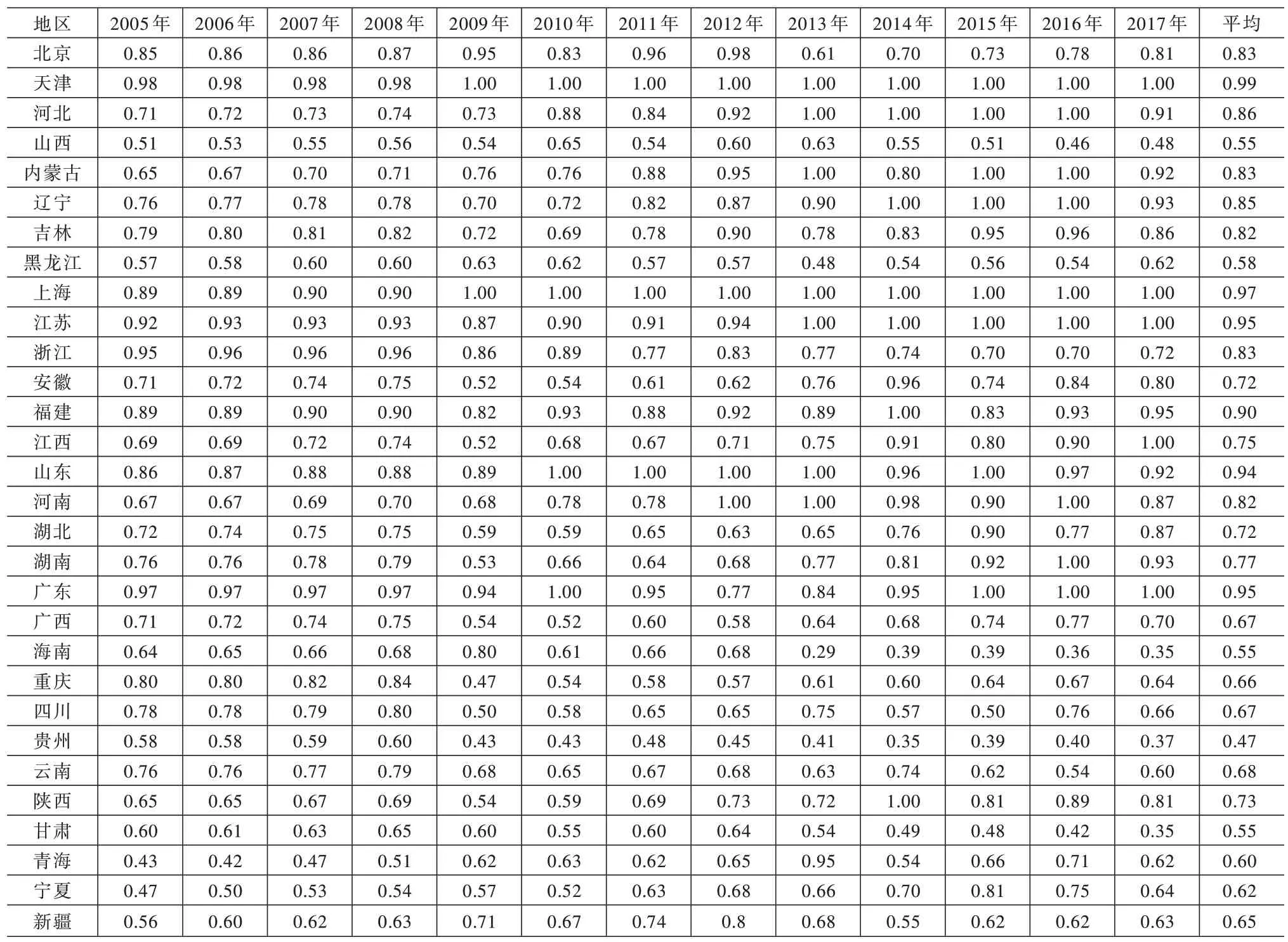
表1 各省份2005—2017 年工业用地利用效率

不难发现：东部沿海地区的工业用地利用效率要高于中部地区，最低的则是西部地区；同时，工业用地效率较高的地区，其经济发展水平同样较高；最后，根据各省份各年工业用地利用效率可得，各省份工业用地利用效率的变化趋势是随时间呈波动状变化。

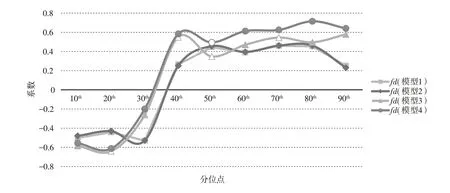
图2 财政分权对工业用地利用效率的影响

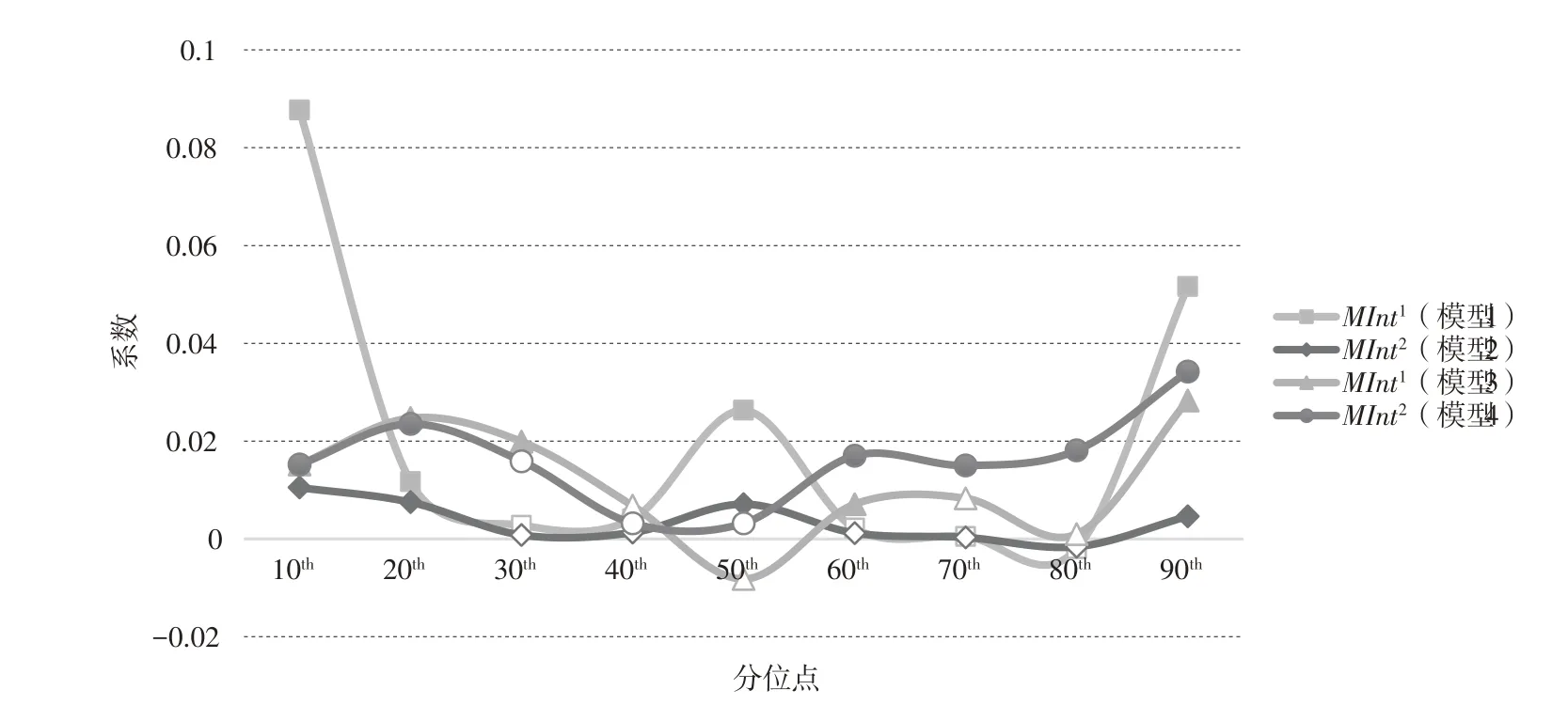
图3 市场整合对工业用地利用效率的影响

（二）面板单位根检验与协整检验

在估计参数之前，需要对面板数据的变量进行平稳性检验。面板单位根检验的结果见表2。本文采用LLC 检验、IPS 检验以及Breitung 检验3 种检验方法，对各变量进行面板单位根检验。通过表2 可以发现，所有的变量在一阶差分下都是平稳的，所有变量的一阶滞后项都在10%的显著水平上拒绝“存在单位根”的原假设。随后，本文需要进行面板协整检验，进而研究变量之间是否存在长期均衡关系。面板协整检验的主要检验方法是Kao residual 协整检验，上述8 个模型的面板协整检验结果见表3。检验结果显示，在模型1～模型3中ADF 统计量均在5%的显著水平上显著，模型4 中ADF 统计量在10%的显著水平上显著，而在模型5～模型8 中，ADF 统计量均在1%的显著水平上显著。由此说明，在样本期内，这些变量存在长期均衡关系。

（三）面板分位数回归结果分析

本文利用面板分位数回归可以研究当工业用地利用效率与工业用地利用效率增长率处于不同分位点时，财政分权与市场整合对工业用地利用效率与工业用地利用效率增长率的异质影响。本文选用2005—2017 年的数据，将工业用地利用效率与工业用地利用效率增长率分成9 个分位点（τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9），构建面板分位数回归模型，模型1～模型8 的回归结果见表4～表11。为了更加直观地反映比较各影响因素在不同分位点水平上对工业用地利用效率与工业用地利用效率增长率的影响差异，并总结规律，将各财政分权、市场整合以及两者的交叉项在不同分位点水平上的估计系数制作成折线图，具体如图2～图6 所示。通过计算结果，本文得出以下结论。

1.财政分权与市场整合对工业用地利用效率的异质性影响

首先，就模型1～模型4 而言，当工业用地利用效率较低时（τ=0.1、0.2 与0.3），财政分权（fdit）的回归系数大部分为负数（系数为-0.6402～-0.1998），且除模型3中0.2 分位点外，在其他分位点上都通过了10%的显著性水平检验。这说明，当工业用地效率较低时，财政分权对工业用地利用效率具有显著的负向影响；而当工业用地利用效率处于中上水平时（τ≥0.4），财政分权的回归系数都为正（系数为0.2301～0.7150），同时随着分位点的上升，各分位点处的估计系数变化逐渐趋于平稳，且大部分都在10%的显著水平下显著，说明当工业用地利用效率处于高分位点时，财政分权对工业用地利用效率具有正向的促进作用，且这种正向促进作用会随着分位点的上升而逐渐平稳（具体如图2 所示）。当工业用地利用效率较低时，政府财政自主度的增加可能会导致政府间产生恶性竞争，造成生产要素与土地资源的不合理利用，从而降低工业用地利用效率；而在工业用地利用效率较高的地区，经济发展水平较高，管理技术经验丰富，财政分权有利于推动地方政府增加科技支出，实现技术进步与科学化管理，从而提升工业用地利用效率。

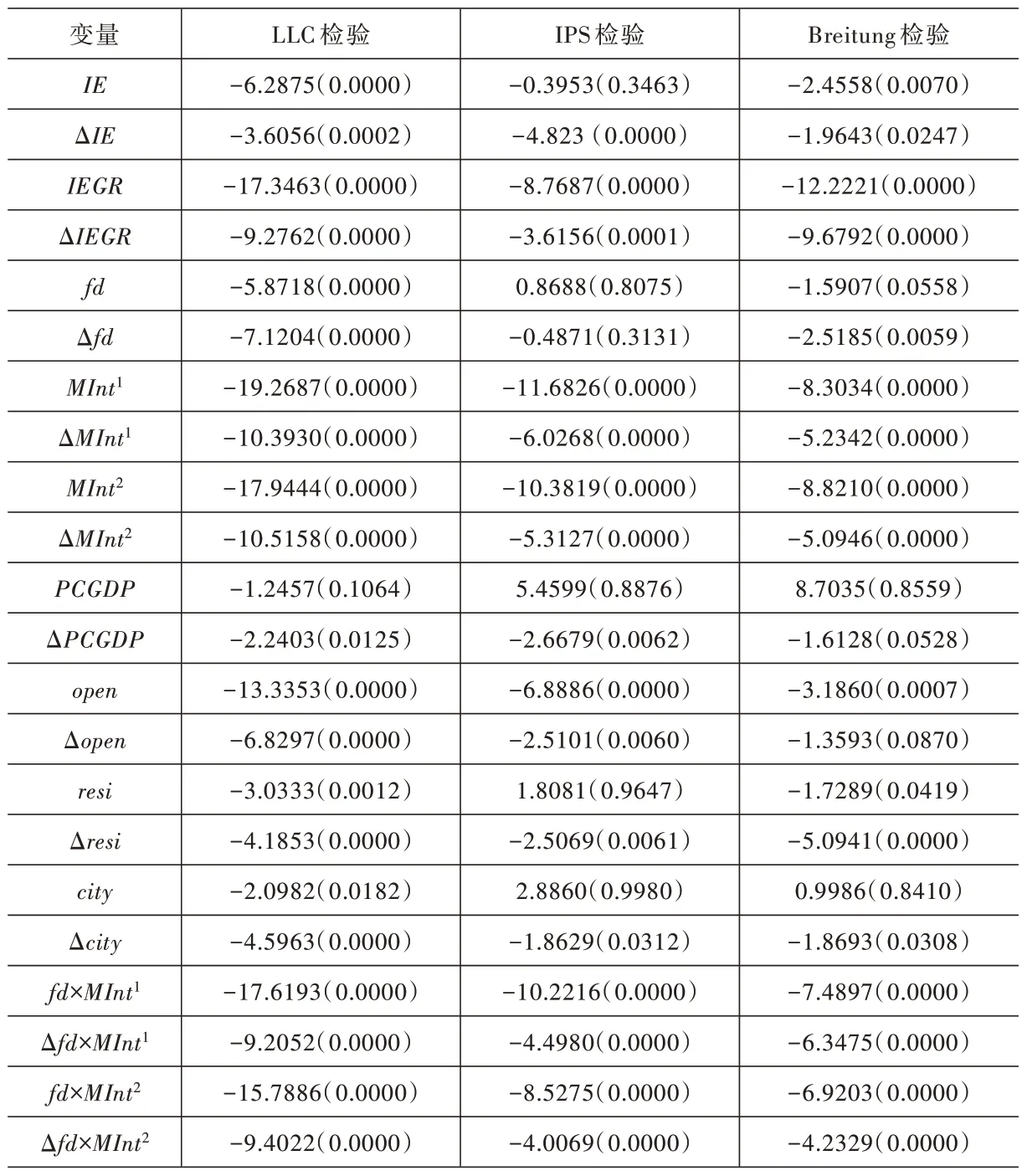
表2 面板单位根检验结果

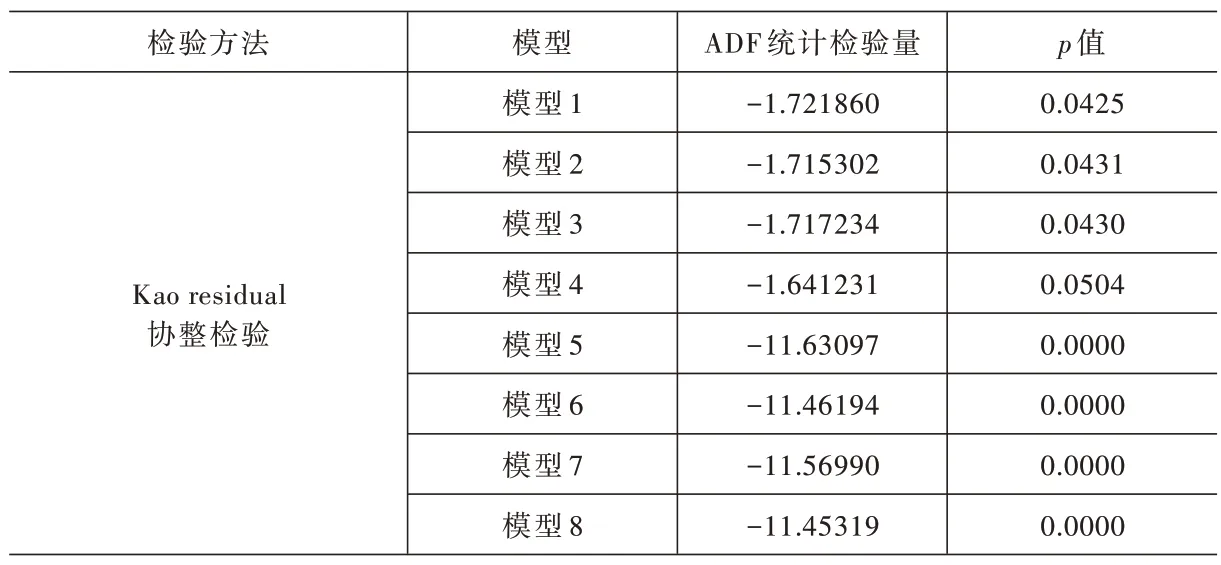
表3 面板协整检验结果

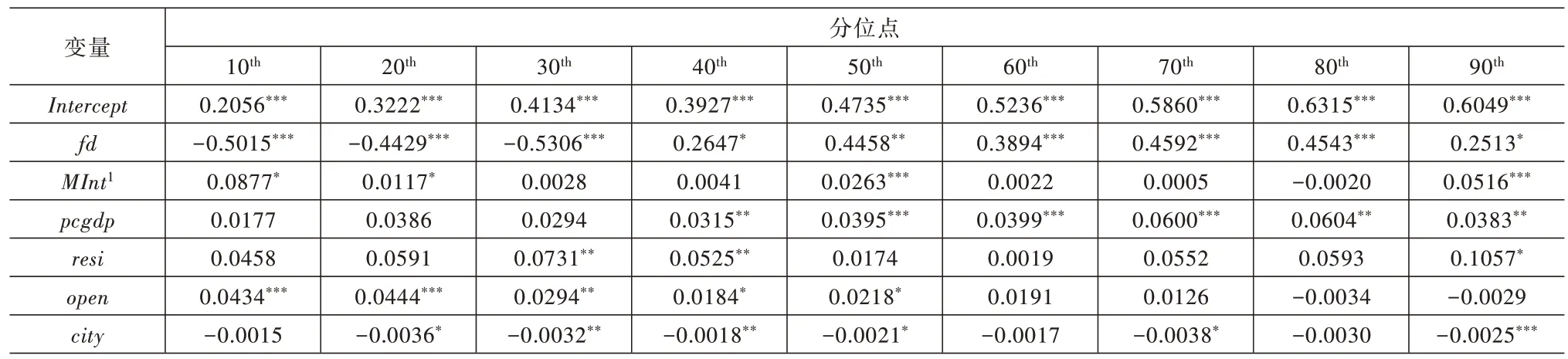
表4 模型1 估计结果

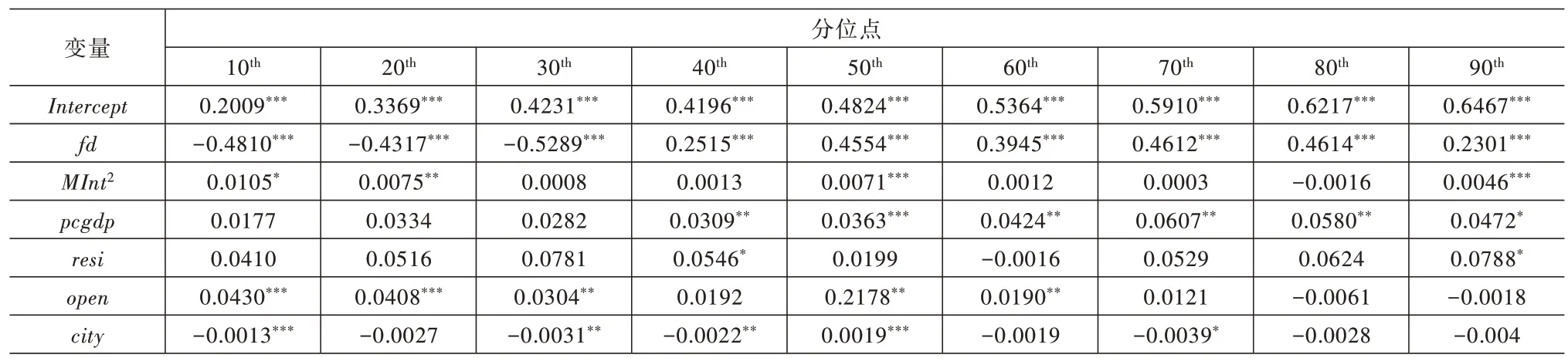
表5 模型2 估计结果

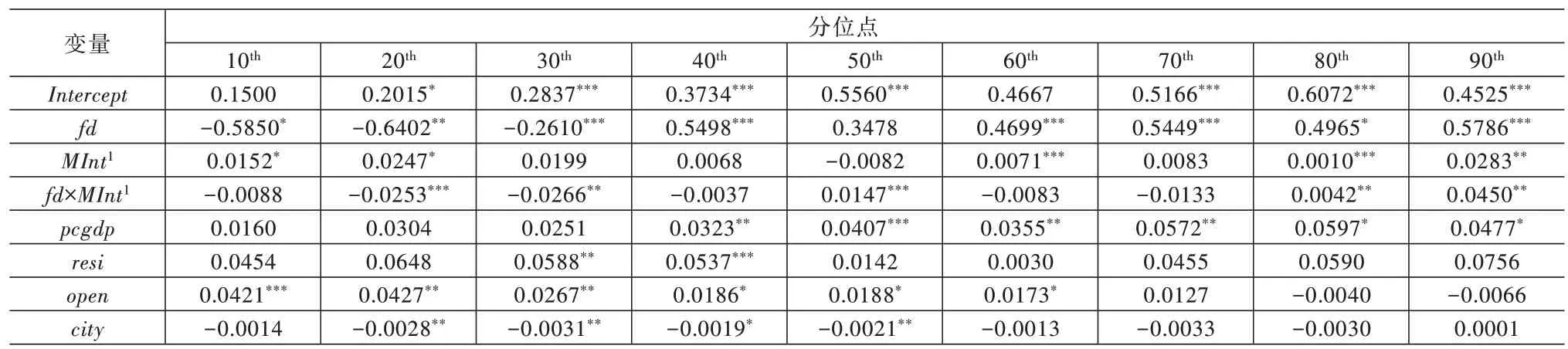
表6 模型3 估计结果

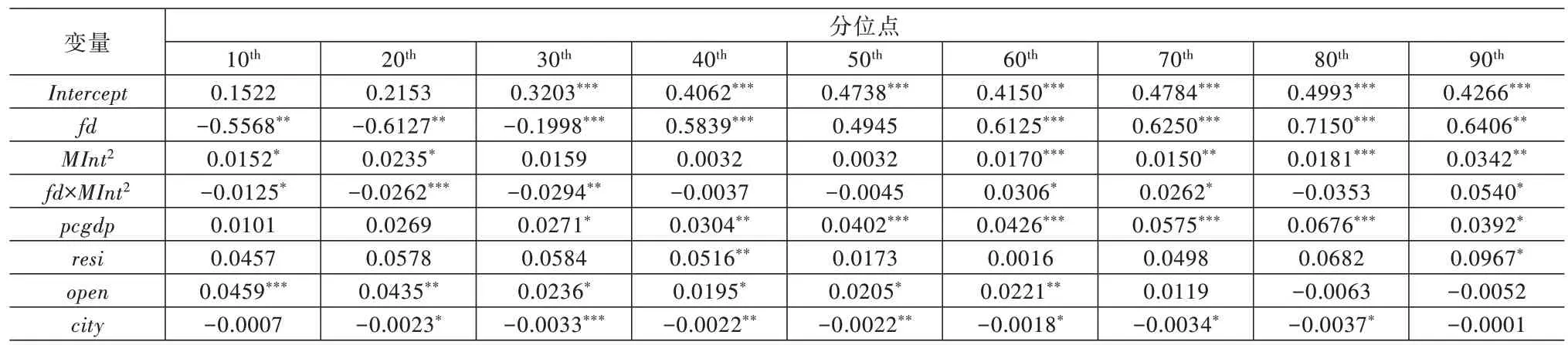
表7 模型4 估计结果

最后，就其他控制变量而言，地方经济发展水平（pcgdpit）在各个分位点的系数均为正，且大部分都在5%的显著水平下显著，说明地方经济发展对工业用地利用效率具有显著的促进作用；而城市化水平（cityit）在各个分位点均为负，且大部分都通过了10%的显著水平检验，说明随着城市化水平的提高，城市扩张与城镇人口比重增加，会对工业用地利用效率产生显著的负向影响；科研投入（resiit）的回归系数在大多数分位点处不显著，原因在于本文选取的科研投入指标包括社会各个行业的总科研投入比例，在某中程度上不能代表对工业发展的科研投入水平，同时也可以说明，国家目前对提升工业用地利用效率的科研投入力度不够，科研投入效果不明显；外资投入大致上对工业用地利用效率具有正向影响。

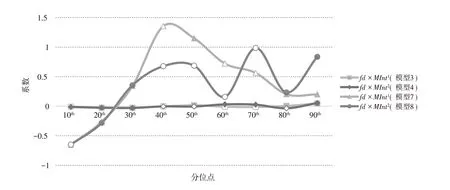
图4 财政分权与市场整合的交互项对工业用地利用效率及其增长率的影响

2.财政分权与市场整合对工业用地利用效率增长率的异质性影响

首先，从图5 可以看出，财政分权对工业用地利用效率增长率的影响大致呈倒“U”型变化趋势，即两端低中间高的变化趋势。值得注意的是在两端的分位点，也就是当工业用地利用效率处于较低或较高水平时（τ=0.1、τ=0.2 以及τ=0.6～0.9），财政分权对工业用地利用效率增长率具有负向影响，且大部分系数都通过了10%的显著性水平检验；当工业用地利用效率处于中等水平（τ=0.3～0.5）时，财政分权的回归系数都为正，此时财政分权对工业用地利用效率增长率具有显著的促进作用。同时，根据图5 也不难发现，财政分权的回归系数在0.3～0.5 分位点处上升趋势明显，在0.6～0.9 分位点处上升且逐渐趋于平缓，这同样说明财政分权对工业用地利用效率增长率的促进作用随着分位点的上升会逐渐减弱，甚至在高分位点处（τ=0.6～0.9），财政分权对工业用地利用效率增长率会产生负向影响。

第二，就市场整合而言，根据表8～表11 可以得出，在模型5 中在0.8 分位数的回归系数估计值为-0.0206；在模型7 中在0.8 分位数的回归系数估计值为-0.9993；在模型8 中在0.7 与0.8 分 位数的回归系数估计值分别为-0.3403 与-1.0080。然而这些系数均为不显著。除此之外，市场整合（与）的回归系数在其余各个分位点处的估计值均为正，说明市场整合通常情况下，对工业用地利用效率增长率存在正向影响。再根据图6 可以看出，市场整合的回归系数大致呈下降趋势，且变化较为明显。说明市场整合对工业用地利用效率增长率的正向促进作用会随着分位点上升而逐渐减弱，市场整合对工业用地利用效率增长率的正向影响在低分位点处作用较强，而在高分位点处作用较弱。

第三，模型7 中，财政分权与市场整合交互项fdit×在0.2 分位点处的回归系数估计值为-0.2635，且在1%的显著水平下显著；财政分权与市场整合交互项fdit×在0.2 分位点处的回归系数估计值为-0.2838，且在1%的显著水平下显著。说明当工业用地利用效率增长率较低时，财政分权与市场整合的共同作用对工业用地利用效率增长率具有负向影响。模型7 中，的fdit×在0.3、0.5、0.8 以及0.9 分位数的回归系数估计值分别为0.3430、1.1496、0.2027 以及0.2004，且都通过了10%的显著水平检验；模型8 中，fdit×在0.3、0.8 以及0.9 分位数的回归系数估计值分别为0.3541、0.2323 与0.8357，且同样都通过了10%的显著水平检验。这说明随着分位点的上升，财政分权与市场整合的共同作用对工业用地利用效率增长率逐渐产生正向影响。此外，如图4 所示，随着分位点的提高，财政分权与市场整合的共同作用对工业用地利用效率增长率的影响相较于其对工业用地利用效率的影响，变化更为显著。

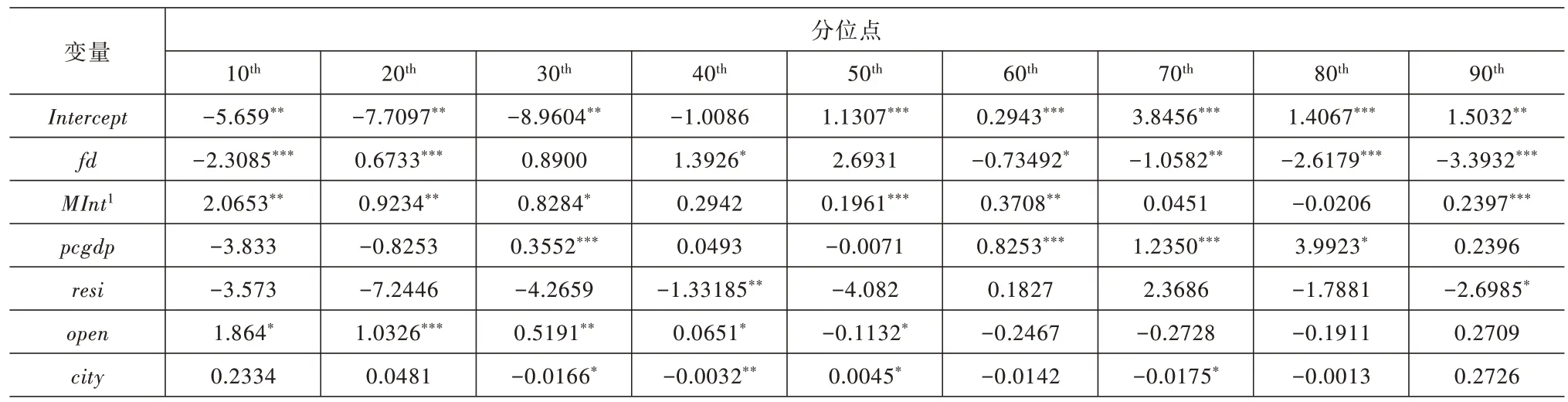
表8 模型5 估计结果

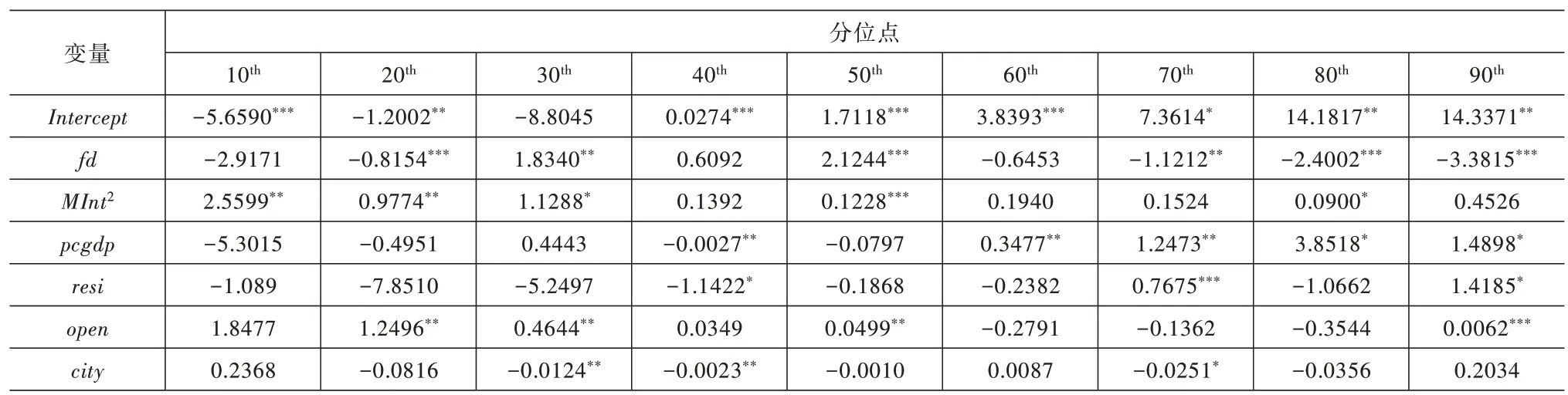
表9 模型6 估计结果

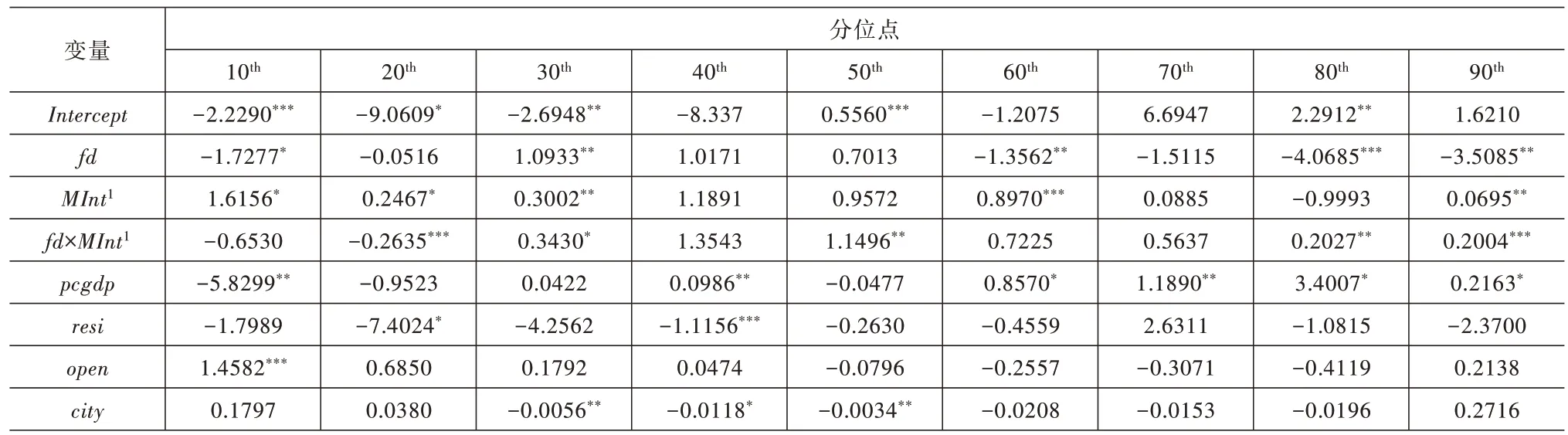
表10 模型7 估计结果

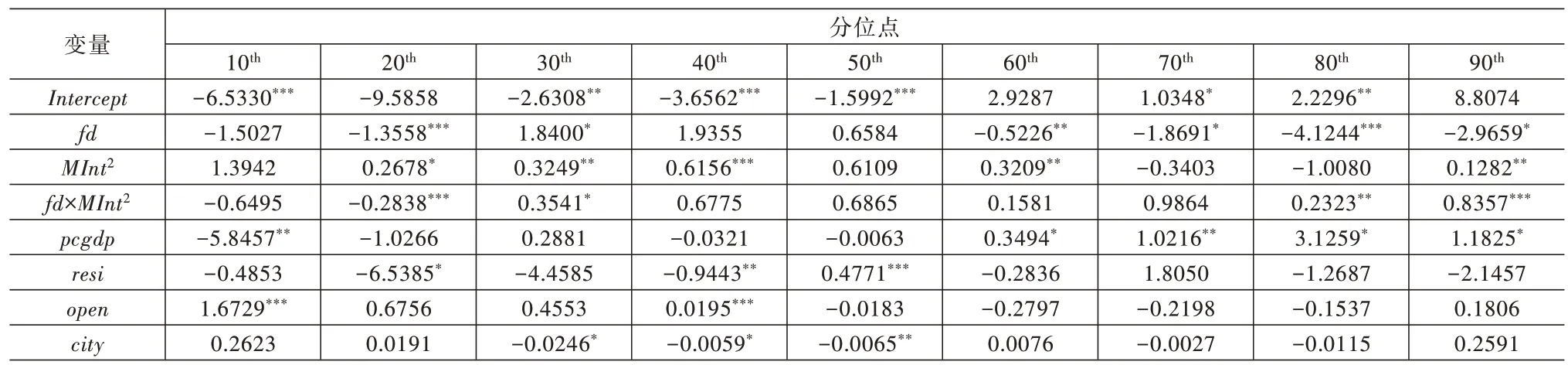
表11 模型8 估计结果

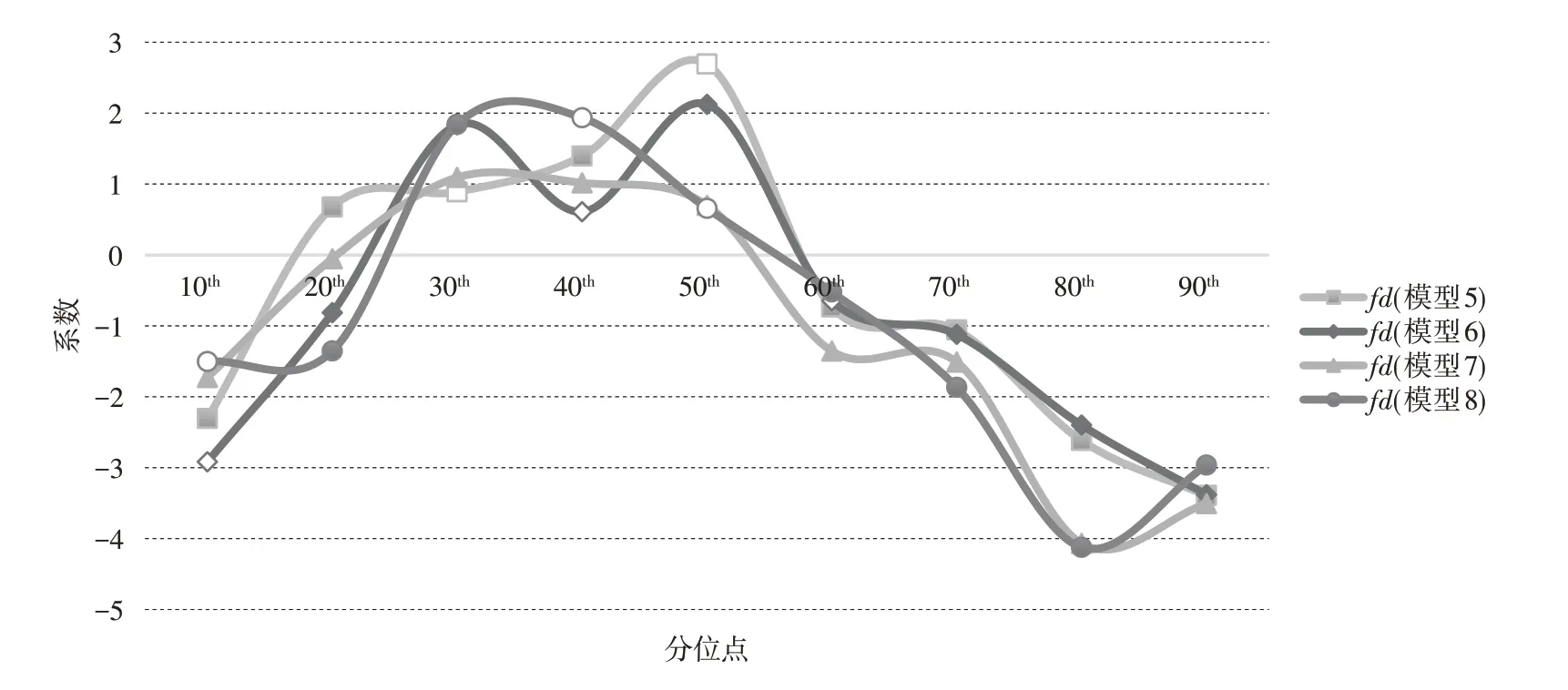
图5 财政分权对工业用地利用效率增长率的影响

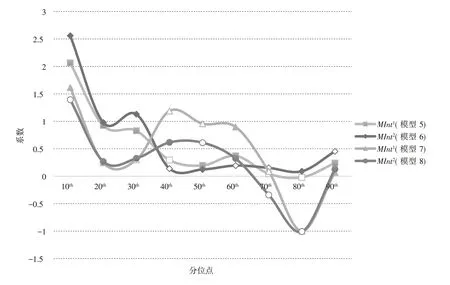
图6 市场整合对工业用地利用效率增长率的影响

五、结论与启示

本文选用2005—2017 年数据，将工业用地利用效率分成9 个分位点（τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9），构建面板分位数回归模型，研究了在不同分位数水平上财政分权与市场整合对工业用地利用效率及其增长率的异质性影响。主要研究结论如下：

（1）当工业用地利用效率较低时，财政分权对工业用地利用效率具有显著的负向影响，在0.1～0.3 分位点处，财政分权对工业用地利用效率的影响系数为-0.6402～-0.1998。而当工业用地利用效率处于高分位点时，财政分权对工业用地利用效率具有正向促进作用，在0.4～0.9 分位点处，财政分权的影响系数为0.2301～0.7150；财政分权对工业用地利用效率增长的贡献会随着分位点的上升而逐渐增大，财政分权对工业用地利用效率增长率的影响随分位点的提高大致呈倒“U”型变化趋势。

（2）市场整合程度的提高可以有效地促进工业用地利用效率提升，随着分位点的提高，市场整合对工业用地利用效率增长的贡献趋于平稳；市场整合对工业用地利用效率增长率的正向促进作用会随着分为点上升而逐渐减弱，市场整合对工业用地利用效率增长率的正向影响在低分位点处作用较强，而在高分位点处作用较弱。

（3）在低分位点处，财政分权与市场整合的共同作用对工业用地利用效率及其增长率具有负向影响（对工业用地利用效率的影响系数为-0.0294～-0.0088；对工业用地利用效率增长率的影响系数为-0.2635～-0.2838）。随着分位点的上升，在高分位点处，财政分权与市场整合的共同作用对工业用地利用效率及其增长率会逐渐产生正向促进作用（对工业用地利用效率的影响系数为0.0042～0.0540；对工业用地利用效率增长率的影响系数为0.2004～1.1496）。随着分位点的提高，财政分权与市场整合的共同作用对工业用地利用效率增长率的影响相较于其对工业用地利用效率的影响，变化更为显著。

综上，由于各地区工业用地利用效率存在差异，政策制定者需因地制宜，制定与各地区发展相适应政策：在工业用地利用效率较低且其增长速度较慢的地区应适当降低地方政府财政分权程度，加大监管力度；在工业用地利用效率较高的地区应适当提升地方政府财政分权程度，简政放权，增加财政自主度，促进地方政府间良性竞争；同时应注重推动市场一体化建设，促进资源合理配置，推动科技进步与技术传播，从而有效提升工业用地利用效率。