垂直扩容垃圾挡坝稳定性离心机试验与数值仿真

周小文，蒋浩然，周 密，程 力，韩泽军

(1.亚热带建筑科学国家重点实验室(华南理工大学)，广州 510640； 2.华南理工大学 华南岩土研究院，广州 510640)

目前，获批一个新的填埋场选址越来越困难，设计者常采用垂直扩容对已有的垃圾填埋场进行扩建.垂直扩容具有充分利用堆填区、降低建造费用、较易获批等优点[1].中国大部分垃圾填埋场均属于山谷型填埋场，在填埋场的坡脚处都建有垃圾坝，因此，在垂直扩容中垃圾坝也需要加固加高以增加填埋场的容量和提供额外的挡土阻力，从而增加填埋体的整体稳定性.垃圾填埋场失稳造成的危害非常巨大[2]，填埋体的整体稳定性问题成为设计和运行中最重要的考虑因素之一，而垃圾坝的设计又是该问题的关键.垂直扩容是高效利用土地的一种方法，可以最大效率地利用土地资源，尤其是对中国人口众多的超级大城市而言.垂直扩容通常可分为两种方案：填土挡坝(通常为均质填土坝)扩容和加筋填土挡坝扩容[3].若填土坝方案不能满足要求或者需要较高的安全稳定性，应考虑加筋填土坝方案，加筋填土坝安全稳定性更高，但是造价相应增加.垂直扩容垃圾挡坝设计在中国暂无专业规范可依，而在美国加筋土坝应用于填埋场扩容较多，表1列出了一些美国垂直扩容填埋场中加筋土结构(在美国“加筋土坝”的称谓不常见，故此用“加筋土结构：geosynthetics reinforced soil(GRS) structures”).在2010年前多为高度小于15 m的小型结构，而后逐渐出现了高度超过20，30 m的大型结构，在中国大型的加筋土垃圾坝应用还未见到报道.

表1 一些美国的垂直扩容垃圾填埋场中的加筋土结构

对填土坝的稳定性研究由来已久，中国土石坝规范[10]通常采用刚体极限平衡分析法，对均质土坝规范推荐采用简化毕肖普法，对于复杂工况的稳定性计算需要采用数值算法，因而通用条分法和有限元得到了广泛应用[11-14].对加筋土坝的稳定分析，当前国内外均无专业规范，而是依据加筋土设计规范[15-17]采用圆弧滑面极限平衡法，无视筋土相互作用机理，把筋材作用当成一种总抗滑力，人为假定其作用点和方向，并按照一定规则分配给各层筋材，这种简化设计方法偏离实际甚远.一些研究者[18-24]采用模型试验和数值模拟考察加筋土结构.在模型实验方面，Zornberg等[19,24]采用离心机模型试验考察了加筋土边坡力学行为以及失稳破坏机制；在数值模型方面，Griffiths等[13-14,25]基于一些简单算例得出在合理处理筋土接触问题后认为将有限元强度折减法用于考察加筋土结构与考察一般土工结构并无本质区别,介玉新等[26]采用用强度折减法对加筋土边坡滑移破坏形态进行了研究.

本文采用离心机试验和有限元数值计算分析对垂直扩容工程中垃圾挡坝的稳定性展开系统研究，研究结论不仅服务于实体工程，并且为加筋土坝推广应用于垃圾填埋场提供借鉴依据.

1 工程背景简介

本工程实例来源于位于广州市东北部郊区的兴丰生活垃圾卫生填埋场，为继上海老港垃圾填埋场后中国第二大的生活垃圾填埋场.2012年该填埋场库容达到饱和，为增加库容在南侧边界新建了一个长300 m、高35 m的垃圾坝来增加750万m3的容量.受南侧既有建筑的限制(见图1(a))，新的垃圾坝边设计成了45°的斜坡并且采用土工布加筋，在坝高5，15和25 m处各设置2 m宽的平台，垃圾坝顶高35 m，宽12 m.坡脚设计了一排灌注抗滑桩，旧坝靠新坝侧局部采用了注浆加固(即图1(b)中的⑤)，坝体下2 m地基换填成高摩擦黏聚材料.土工布极限抗拉强度为500 kN/m，其5%伸长率时的抗拉强度为285 kN/m，厚度为2 mm，垂直间隔0.5 m布置，覆盖新坝全部区域，坡面处反包土工布.各土层分布见图1(b)，其中①为地基下层土，主要成分为微风化花岗岩；②为地基上层土，主要成分为花岗岩残积土；③为地基换填土，主要成分为粗细颗粒混合填料；④为旧坝，主要成分为粗细颗粒混合填料；⑤为旧坝局部加固区，采用水泥注浆加固；⑥为新坝，主要成分为粗细颗粒混合填料；⑦为垃圾土，旧坝左侧垃圾土为已堆放的垃圾土，新坝左侧垃圾土为未来将堆放的垃圾土；⑧为抗滑桩，桩型为直径1.6 m、中对中桩间距1.8 m、桩长18 m(入岩3 m)的冲孔灌注桩.地下水位处于地面以下2 m.

图1 垃圾坝

2 离心机模型

2.1 模型与材料

诸多研究采用了离心机模型来考察加筋土结构性能，Zornberg等[18]指出尽管离心模型有一些缺点如非均匀加速场、边界效应、尺寸效应等，离心机实验为缩尺模型保持与原始模型相同的应力状态提供一个有效的途径.本文建立两个离心机模型以考察坝体在有和无加筋情况下的变形和可能出现的破坏模式.

实验采用了长江科学院CKY-2OO离心机，其有效容量200g·t，最大加速度200g，配有模型箱长1.0 m×宽0.4 m×高0.8 m.本实验采用100g的模型，即缩尺比率为1∶N=1∶100，图2为离心机模型横断面.实体工程中由于下游场地限制，仅能设置一排抗滑桩，但是挡坝与垃圾体非常巨大，单排抗滑桩对其稳定性影响有限.为了较保守地评估垃圾挡坝的稳定性(抗滑桩的效果将在数值模型中考虑和分析，且获得的结论也证明了单排抗滑桩阻抗滑动效果有限)，离心机模型仅模拟图1的新旧坝和垃圾土，图2中①为旧坝，②为新坝，③为垃圾土.离心模型试验为了保守评估垃圾挡坝的稳定性，未考虑抗滑桩，抗滑桩影响作为安全储备.坝体材料取自实际工程选用的粗细颗粒混合填料(剔除粒径大于30 mm的土粒)，级配曲线见图3，经击实实验测得填料最大干密度为1.92 kg/m3,最佳含水率为(15.7±2)%，排水直剪强度指标c，φ为29.5 kPa、36.4°.垃圾土采用松散的粉细砂模拟(仅模拟垃圾土对挡坝的土压力作用而忽略对垃圾土本身的力学性能模拟，粉细砂产生的推力略高于实际垃圾土，从而确保离心机试验是保守评估垃圾挡坝的稳定性)，平均密度为1.72 kg/m3.通过窄条拉伸实验和筋-土界面直剪实验筛选确定使用0.45 mm厚的涤纶来模拟2 mm厚的土工布，模拟依据筋-土界面摩擦相似和单位面积抗拉强度等效，即

式中：cs-g，p、φs-g，p为土工布-土界面黏聚力和内摩擦角，由筋-土界面直剪实验得为10.14 kPa、35.1°；cs-g，m、φs-g，m为涤纶-土界面黏聚力和内摩擦角，由筋-土界面直剪实验测得涤纶-土界面有相近的数值，为9.5 kPa、34°；T5%，p为土工布5%伸长率抗拉强度，其值为285 kN/m，Sv，p为土工布竖向间距，其值为0.5 m，T5%，m、Sv，m为涤纶的上述对应参数，其值分别为28.5 kN/m、0.05 m.坝体土按0.05 m分层在最佳含水率时人工锤击压实到密度≥1.85 kg/m3.涤纶按0.05 m一层铺设，在坡面进行反包以模拟实际工程中的土工布反包工艺.由于离心机模拟渗流非常复杂且实体工程中垃圾堆体有设置排水井用以降低垃圾堆体中的地下水位，施工期和正常运营期排水井都有水泵抽水，且整个垃圾体由防渗膜隔离与外界地下水断开，其内部水仅由垃圾降解产生，其水量有限，通过水泵不间断抽水完全可以正常排出，故而其正常工况的地下水位较低，这正是离心机模型中不考虑渗流影响的原因.而数值模拟对当垃圾体四周防渗膜破损的极端工况进行模拟，地下水进入垃圾体，考虑该极端情况下不同水位(渗流)对垃圾挡坝的稳定性影响.

图2 离心机模型横断面示意

图3 挡坝土样级配曲线

2.2 测试与结果

在坡面设置5个激光位移监测点以测量坡面水平和竖向位移，水平监测点为图2中D2和D4，竖向监测点为图2中D1、D3和D5.图4为两个模型的加速过程，按20g每级逐级提高，每增加一级加速度稳定7 min后开始增加下一级，直到增加至100g，运行持续一定时间，观察模型是否破坏.从图5可以看出，两个模型均未发生破坏，忽视垃圾堆体的变形，仅考虑坝体变形，图6中模型1(有加筋)和模型2(无加筋)最大沉降量分别为8.8，9.7 mm；最大水平位移量分别为10.1，12.6 mm；最大沉降点均为点D5，最大水平位移点均为点D2；在100g离心加速度运行阶段，监测点的位移量基本保持平稳.离心机实验表明，有无加筋时坝体均不会失稳，这证明了采用粗细颗粒土料作为加筋土填料的可行性.此外，土工布加筋能明显减小坝体的水平位移，相比无加筋坝，加筋坝水平位移量减少19.8%，这与Hu等[23]通过位移场评估加筋效果的结论类似.

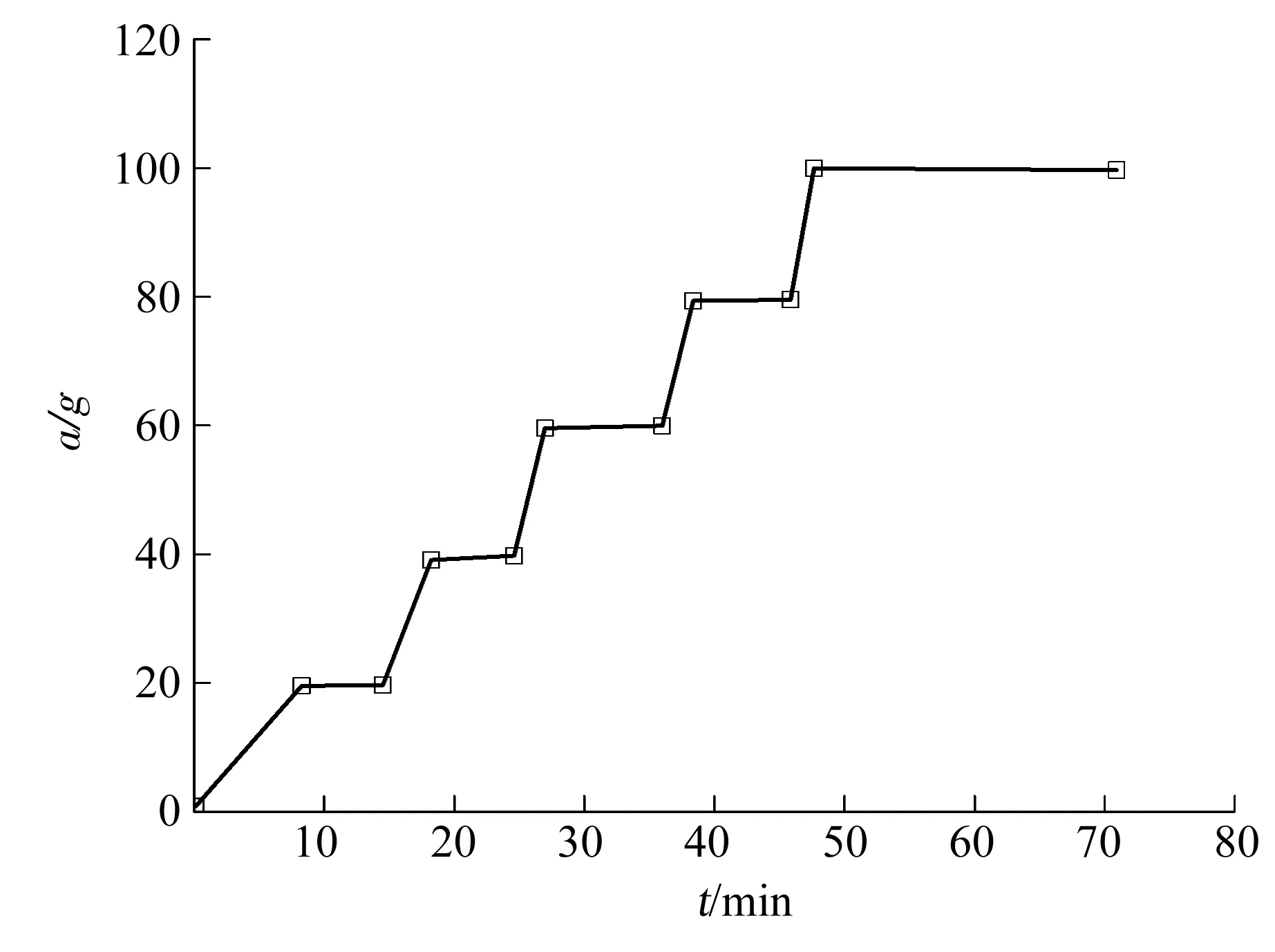
图4 离心加速度历时曲线

图5 模型在t=70 min时的照片

建立与离心机模型尺寸相同的数值模型(模型设置与材料取值见第3节)，通过重力加载至100g可获得位移场(见图7).从挡坝水平总位移场可以看出：最大水平位移发生在高10～20 cm的坡面附近，与离心机模型监测到的最大水平位移点D2(h=10 cm)接近(见图7(a))，最大水平位移量数值解为11.3 mm，接近D2实测值10.1 mm(见图6(a))；最大竖向位移发生在坝顶(不考虑垃圾堆体变形)，与离心机模型监测到的最大竖向位移点D5(h=35 cm)在同一高程(见图7(b))，最大竖向位移量数值解为9.3 mm，接近D5实测值8.8 mm(见图6(b)).

由此可以看出，本文建立的数值模型能较好预测加筋挡坝的变形规律.为了进一步考察加筋土坝在实际工况下的稳定性和破坏机理，将利用后续所建立的有限元数值模型进行分析.

图6 监测点位移-时间曲线

图7 挡坝数值位移场与监测点实测值对比

3 有限元数值模型

3.1 模型的建立

采用Plaxis2D有限元软件建立二维的平面应变数值模型，为减少边界尺寸效应，设置模型底边长550 m，左侧高135 m，右侧高25 m.采用标准的平面应变位移边界，左侧与底部为不透水边界，其余均为透水边界.土体采用15节点三角单元，土工布采用5节点线单元，桩采用板单元.按中等密度[28]划分网格单元，单元总数为4 965，节点数为40 199.有限元模型的单元网格如图7所示，土工布用土工布单元模拟，土工布与土体摩擦接触，摩擦系数比依据筋-土界面直剪实验测得为0.6, 该系数来源于室内模型试验测试结果.

3.2 本构关系和材料属性

土体采用摩尔库伦模型，剪胀角设为0，这与使用不相关联的流动准则一致.土工布采用理想弹塑性模型，轴向刚度EA=1 000 kN/m；出于保守考虑，土工布拉力强度限值Np=200 kN/m以模拟土工布的受拉屈服(土工布5%伸长率时实验抗拉强度为285 kN/m，见前文第1节).桩设为各向同性弹性体，轴向刚度EA取为2×104MPa×3.14×(0.8 m)2/(1.8 m)=2.23×107kN/m，抗弯刚度EI取为2×104MPa×3.14×(1.6 m)4/(64×1.8 m)=3.57×106kN·m2/m，泊松比取为0.2，则等效板厚deq=(12EI/EA)0.5=1.39 m.土层参数取值依据现场测试和室内试验而定，土体的不均匀性会影响计算结果[32].为了简化模型，不考虑土体的不均匀性，取值汇于表2，其中土的渗透系数设置为各向同性参数.

3.3 计算工况

为考察施工阶段和运营阶段坝体稳定性，建立10个计算工况，见表3.其中工况1,2,3,4分别对应新坝填筑至5，15，25，35 m高处；工况5，6，7对应新坝左侧垃圾土堆载至第3，5，7层，即垃圾土堆至新坝左侧28，30，35 m高处；工况8，9，10对应运营期垃圾土中水位上升(对应垃圾体周围防渗膜破损的极端工况，外界地下水进入垃圾体，且坝面防渗膜破损，坝体发生渗漏，该类工况是实际运行构成中的极端风险工况)可能引起坝体出现的3种稳态渗流情形，3个渗流场是基于模型左侧边界水头高32，42，59 m作入渗点(见图8，溢出点由计算确定)的3种水力条件计算而成；工况1～7中考虑水位-2 m，即水位于地面以下2 m.对每个工况先进行塑性(即弹塑性变形)计算，再进行安全性分析，在工况1之前对已有的土层和结构通过重力加载生成初始应力.土工布和桩输入值为保守考虑的长期强度设计值，故安全计算时不参与折减.本文不考虑垃圾堆体的稳定性，为了排除垃圾土内部破坏对计算收敛的影响，垃圾土也设置为不参与强度折减.

表2 计算参数

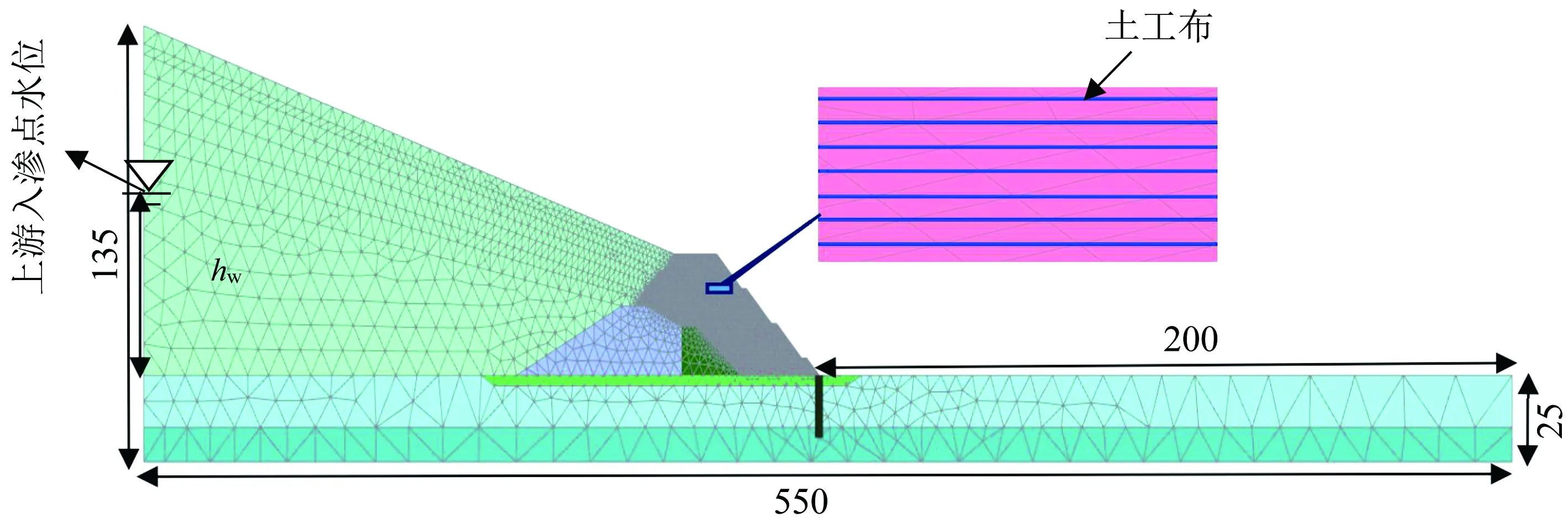
图8 典型有限元模型网格(m)

表3 参数分析计算工况汇总

4 数值仿真结果分析

计算得到的安全系数由Plaxis中总乘子∑Msf给出，潜在滑移面用剪应变增量Δγs云图呈现.图9显示了各工况下潜在滑移面的形状和位置及安全系数.

图9 各工况下的潜在滑移面

由图9可以看出，潜在滑移面主要位于旧坝与地基上层土范围内，仅有局部出现在新坝区域内；在新坝填筑阶段即工况1～4，随着坝体筑高滑移面由深向浅发展，抗滑桩应力集中越来越明显，其对增量剪应变分布的干扰也越突出，使得桩附近的滑移面不易辨识；在垃圾土堆载阶段即工况5～7，随着堆载进行滑移面逐渐变陡，左上部穿过新坝区域并与新坝左侧和垃圾土交界面贯穿，由于抗滑桩的存在，桩头(即坡脚)处出现新的滑移面迹象.总体而言，当坝体内无渗流时安全系数均大于1.8，由于2D模型忽略了土的空间不均匀性对最不利计算断面带来的不确定性，2D模型计算得到的安全系数通常较3D稍微偏大(约15%以内)(Liu等[32])，扣除15%的干扰坝体无渗流时计算得到的安全系数仍然满足≥1.5的保守要求.

当坝体内出现渗流时安全系数急速下降，工况8，9，10的安全系数分别降至1.47，1.264，1.18，这表明垃圾堆体中出现高于32 m的水位时，若衬垫发生泄漏引起坝体渗流则坝体安全储备不够，因此，坝体运营时应严格控制垃圾堆体中的潜水位在32 m高程(相对地面而言)以下.

为了进一步考察坝体渗透系数、地基(含旧坝)加固措施、新坝填料强度参数、筋材刚度和布置对整体稳定性的影响，分别建立不同的数值模型，计算不同变量下各工况的安全系数.

5 参数分析

5.1 坝体渗透系数

以图8模型为原型，保持3种初始水位线(工况8，9，10)不变，将新坝、旧坝(含加固区)土体分别取不同的渗透系数以分析渗透强弱对边坡稳定性的影响.图10，11显示安全系数随着土体渗透系数增大先减小后增大，当坝体的渗透系数接近地基上层土时，即在5×10-3～1×10-2m/d时，安全系数降至最小即坝体受渗流影响最显著；当坝体的渗透系数小于地基渗透系数1个数量级以上时，坝体上游入渗水位虽然高，但坝体内浸润线快速降低，安全系数反而较大；当坝体的渗透系数大于5×10-2m/d时，坝体相当于透水坝，上游入渗水位低，坝体内浸润线也低，坝体多数区域不受水的影响，因而安全系数也较大.图11表明坝体中稳态水压等势线形状随着土体渗透系数增大先呈凹状后呈凸状；浸润线进入坝体的起始点高度随着土体渗透系数增大而降低，这与张晓咏等[33]采用ABAQUS进行渗漏作用下的边坡稳定分析得到的结果一致.

图10 安全系数与坝体渗流系数之间的关系

图11 工况8下不同渗透系数时稳态孔压等势线

5.2 加固措施

由图1可知，本工程采用了3项加固措施，分别为换填浅层地基土(简称换填)、注浆加固局部旧坝(简称加固)、在新坝坡脚处采用抗滑桩(简称加桩).为评估各项加固措施对坝体整体安全系数的影响，建立了6个计算方案(见表4)的数值模型进行对比分析，其中方案1不采用任何加固措施，方案2仅采用换填(图1中的③)，方案3仅采用抗滑桩(图1中的⑧)，方案4仅采用注浆加固局部旧坝(图1中的⑤)，方案5采用加固和换填，方案6采用加固、换填、加桩3种措施.图12给出了各方案在上述10个工况下计算得到的安全系数.各方案在各工况下的安全系数整体呈下降趋势，其中方案1，2，3在工况1下的安全系数明显低于其他方案，方案1，2，3旧坝未采用注浆加固措施，滑移面经过该区域，而方案4，5，6采用了注浆加固措施，滑移面位于加固区右下方(见图9(a))；在坝体渗流阶段即工况8～10，随着水位的升高坝体安全系数急速下降.对比方案1和6在3个典型工况4，7，8下滑移面位置和形状(见图13)可知，方案1在各工况下滑移面位置相对方案6要浅，并且穿越新坝上部加筋区，而方案6的滑移面基本不穿过新坝加筋区；方案1的滑移面接近坡脚，因其无桩基应力集中的影响，在坡脚附近的滑移面较方案6明显清晰.由于挡坝下游场地限制仅能于坡脚设置一排抗滑桩，且抗滑桩若设置在坡中桩基施工会破坏土工布，垃圾堆体及挡坝体量大等因素，单排灌注桩的抗滑稳定效果有限，未能完全阻断滑动面，故而并没有对挡坝的破坏模式

表4 不同的加固措施对应的计算方案

图12 各方案的安全系数随工况变化

造成明显改变，抗滑桩的使用仅仅作为安全储备.Ho[34]的研究显示，当抗滑桩位于坡体中部时才能起到最佳的抗滑稳定效果，而当抗滑桩位于坡脚时，仅能辅助提高稳定性，无法完全改变边坡的滑动模式.该结论与本项研究的结论一致.

5.3 新坝填料抗剪强度

为考察新坝填料的抗剪强度对坝体整体稳定性的影响，建立以方案1为原型的数值模型，分别改变c、φ的取值，计算坝体在填筑施工完毕(即工况4)、垃圾土堆载完毕(即工况7)和坝体发生低水位渗流(即工况8)时的安全系数，计算结果见图14，15.结果表明，在φ=36°时c从5 kPa增大到50 kPa，3个工况安全系数分别提升5%、6%和7%.在c=30 kPa时φ从10°增大到50°，3个工况安全系数分别提升23%、21%和18%.这与Zheng等[35-36]观察到的加筋土桥台变形对φ较为敏感类似.Zheng等[35]采用FLAC对加筋土桥台进行数值分析时发现填料的c(在0～75 kPa变化)对加筋土桥台的水平位移影响大于竖向位移；Zheng等[36]进一步研究填料的c(在0～12 kPa变化)、φ(在38°～50°变化)对加筋土桥台的水平和竖向位移的影响发现，c仅在高围压下有一定的影响，而φ在高、低围压下的影响均较明显.

图14 在c=30 kPa时安全系数FS与φ的关系

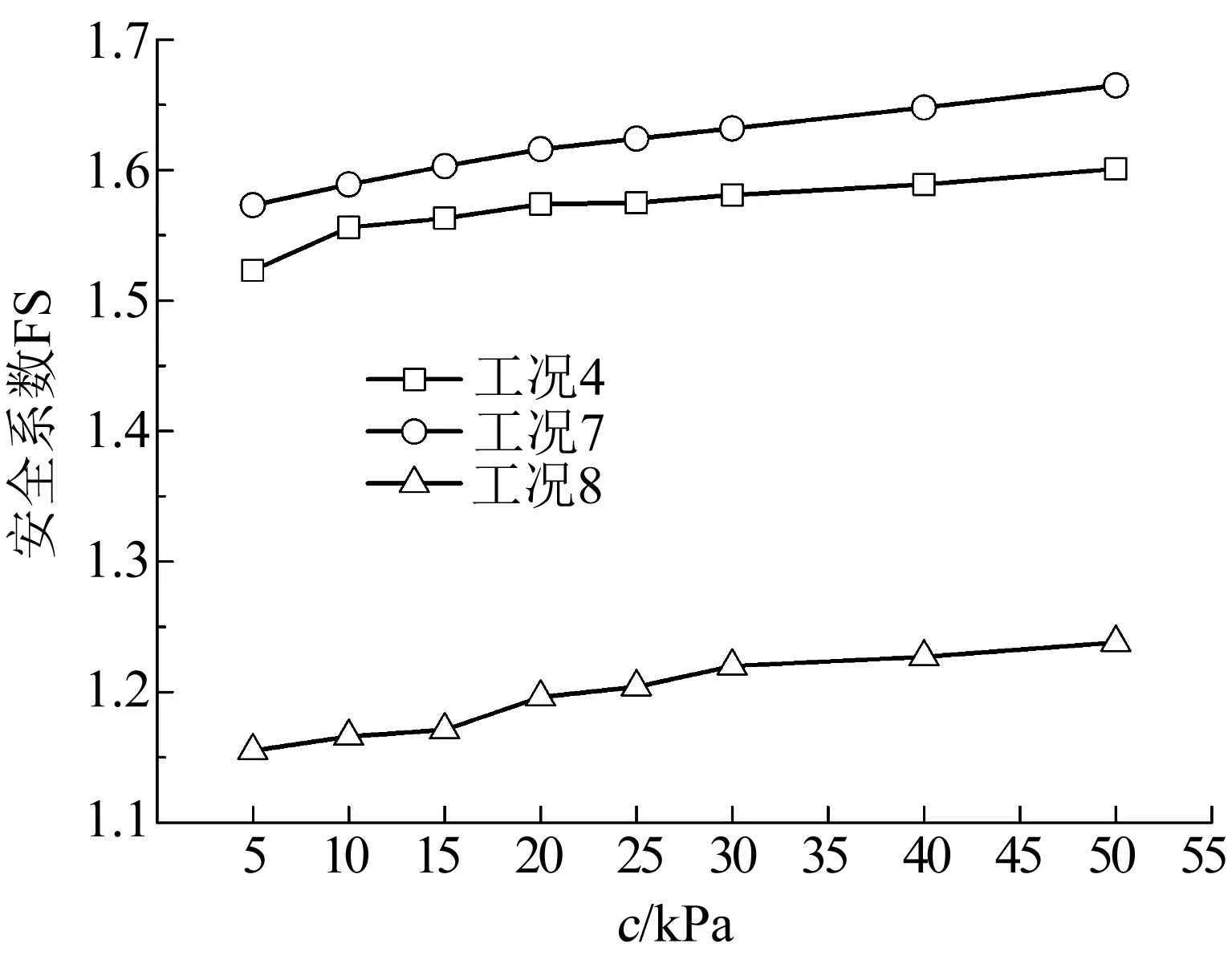
图15 在φ=36°时安全系数FS与c的关系

5.4 筋材刚度

为考察筋材刚度对坝体整体稳定性的影响，建立以方案1为原型的数值模型，改变EA的取值，计算坝体在填筑施工完毕(即工况4)、垃圾土堆载完毕(即工况7)和坝体发生低水位渗流(即工况8)时的安全系数，计算结果见图16.可以看出，筋材刚度对坝体整体稳定性的影响较为明显，尤其是筋材刚度在数量级102范围内变化时，安全系数变化较大，而在数量级103范围内变化时，安全系数变化较小；坝体发生渗流(如工况8)时，采用高刚度筋材对提高坝体整体稳定性仍然效果显著.Zheng等[35]采用FLAC分析筋材的刚度对加筋土桥台的水平和竖向位移的影响时发现，随着筋材刚度由500 kN/m增大至2 000 kN/m，水平位移由48.6 mm降低至27.2 mm，竖向位移由66.4 mm降低至49.8 mm，而当筋材刚度大于1 500 kN/m时竖向位移减少的效果不再明显，这与本文观察到的规律基本符合.此外，Zornberg等[18]通过加筋土边坡的离心模型实验发现，增加筋材刚度能显著提高边坡破坏时的重力加速度水平.

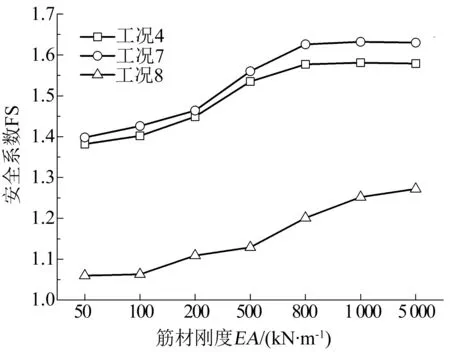
图16 安全系数FS与筋材刚度的关系

5.5 筋材布置

为考察筋材垂直布置对坝体整体稳定性的影响，建立以方案1为原型的4个数值模型，分别模拟筋材间距为0.5，1.0，1.5 m和无加筋4种情况，计算结果见表5.考察筋材水平布置对坝体整体稳定性的影响时，建立以方案1为原型的4个数值模型，分别模拟筋材长度(从新坝右侧向左侧计算)为11，21 m和满铺3种情况，计算结果见表6.结果表明，随着筋材间距变大各工况下的安全系数降低，尤其在坝体发生低水位渗流(即工况8)时安全系数显著下降，甚至在筋材间距由0.5 m变为1.0 m时工况8下的坝体由稳定变为破坏；随着筋材长度变小各工况下的安全系数降低，但在坝体发生低水位渗流(即工况8)时坝体仍然未失稳，在筋材长度11和21 m两种情况下的安全系数和滑移面非常接近，而在满铺情况下的安全系数显著提高，滑移面也不同于前两者，滑移面坡度变得陡峭，上部穿越加筋区域，底部穿越基础更深区域，见图17.

表5 不同筋材间距计算得到的安全系数

表6 不同筋材长度计算得到的安全系数

图17 不同筋材长度在工况4,7,8下滑移面对比

Leshchinsky等[37]基于拉拔实验考察了单层加筋和双层加筋拉拔过程形成的剪切带和破坏形式，其结果显示双层加筋时，两层筋材和中间土体在实验过程中始终保持整体运动，这验证了本文采用筋土变形协调假设是合理的，同时可推断出0.5 m的筋材间距可使筋土保持较好的整体性.Morsy等[38]采用数值方法对比分析两个高均为6.85 m加筋土墙的水平变形测量值，结果显示筋材间距为0.2 m的加筋土墙水平变形的测量值和数值解均明显小于筋材间距为0.4 m的加筋土墙的相应数值，并指出筋材间距小于0.6 m筋土始终保持整体运动.Zheng等[35]对加筋土桥台分析时发现增大筋材长度(从0.3倍墙高变化至1.1倍墙高)能减少加筋土桥台的水平和竖向位移，但当长度大于0.5倍墙高，继续增大筋材长度以减少变形的效果将不明显，即出现临界长度，而本文未观察到临界长度，其原因可能是坝体的特殊外形使得新坝筋材满铺方案更贴合实际工程需求.

6 结 论

1)加筋能明显减小坝体的水平位移，提高坝体稳定性.

2)当垂直扩容时，土工布可有效提高挡坝稳定性，能适应陡峭坝体建造，满足工程需要.

3)文中所述的换填、加固和加桩3项加固措施不仅提高了坝体的安全系数，且对潜在滑移面的位置和形状也有较大影响.

4)对于本文中的该工程，离心机结果显示素填土坝方案能满足工程基本要求，但是加筋填土坝方案安全系数更高，能更好地满足工程的高标准要求.