基于PSO-LSSVM的砂层可注性预测模型及其敏感性分析

朱光轩，张庆松，刘人太，张连震，郭焱旭

(1. 山东大学 岩土与结构工程研究中心，济南 250061； 2.纽卡斯尔大学 工程与建筑环境学院，澳大利亚 纽卡斯尔；3.中国石油大学(华东) 储运与建筑工程学院，山东 青岛 266580)

渗透注浆是在满足地层可注性条件下，将浆液注入地层空隙，从而达到降低土体渗透性、提高土体强度的目的[1].目前，渗透注浆技术已在各类岩土工程中得到了广泛应用[2-6].与化学浆液相比，水泥浆液价格低廉，环境友好，其应用最为广泛.满足地层可注性标准是渗透注浆工程设计首要前提，因此，对于水泥浆液渗透注浆可注性的研究具有重要意义.

水泥浆液可注性影响因素众多、机理复杂，导致其准确评估困难.诸多学者基于可注性室内试验，各自提出相应的可注性评价模型.Burwell等[7]基于大量可注性试验数据提出相应的可注性模型，该模型定义如下：当D15/d85>25、D10/d95>11时，为可注；当D15/d85<11时，为不可注；当1110即可判定为可注.Krizek等[9-10]总结提出了与Burwell类似模型.Akbulut等[11]考虑浆液水灰比及砂层相对密实度等参数，提出了低压(p<200 kPa)注浆下的可注性标准.

经历了家道中落的鲁迅厌恶了周围熟悉的人群,为摆脱这种旧有的人事关系和改变自己的命运，1898年，鲁迅前往南京寻求别样的人生,并先后进入江南水师学堂、江南陆师学堂附设的矿路学堂学习。在此期间，学习的鲁迅接触到维新变法的宣传刊物《时务报》，作为热血青年的鲁迅，救国救民的壮志开始生根，受惠于维新变法派留学生的变法举措留学日本。就这样，鲁迅抱着寻求新知、拯救过敏的热情来到了东京。鲁迅进的第一所预备学校是东京弘文学院,并加入了革命团体浙学会，成为一个激进的革命者，且颇为勇敢。从剪辫子事件就可看出，在剪辫之后不仅毫无畏惧，还特地“断发照相”，以资纪念，并题了一首诗——自题小像，赠给友人许寿裳。诗云：

以上研究皆是基于室内可注性试验结果提出的可注性分类研究方法，然而不同学者提出的可注性分类标准不尽相同.其原因主要为，在渗透注浆过程中，水泥颗粒由于受砂土骨架的阻挡，将发生明显的滤过效应，表现为随注浆进行，砂层孔隙率持续衰减，最终造成浆液扩散存在极限扩散距离[12-15].浆液极限扩散距离大小取决于浆液性质、被注介质性质和注浆压力等参数，在可注性试验中，若被注试样尺寸小于或等于浆液极限扩散距离，则浆液将在整个试样中充分渗透扩散，即表现为可注，反之为不可注.可注性分类标准各不相同，不利于其在实际工程中的推广应用.因此，建立具有普适性的可注性量化评价模型具有重要意义.

为量化评价砂层可注性，开展了可注性室内试验，以水泥浆液水灰比RWC、相对密实度Dr、细颗粒(直径<0.075 mm)含量θ、砂层特征粒径D10和D15为控制变量，测量记录浆液渗透扩散距离，以扩散距离作为可注性量化评价指标，分析得到了各因素对可注性的影响规律.

将粒子群算法(PSO)和最小二乘支持向量机(LSSVM)相结合，通过粒子群算法搜索最佳的支持向量机(SVM)的参数，提出了浆液扩散距离预测的粒子群最小二乘支持向量机方法(PSO-LSSVM).以可注性室内试验测试结果作为训练、测试样本，最终建立了基于PSO-LSSVM的浆液扩散预测模型.在此基础上，根据浆液扩散状态定义可注性分类临界指标，进而建立了相应的可注性分类模型.以测试集试验数据为样本，将可注性分类模型预测结果与现有可注性评价方法进行了对比分析.

砂层可注性影响因素众多，分析可注性各影响因素的敏感性分布对实际工程中注浆参数优化调整具有指导意义.现有研究多为可注性分类预测，缺乏可注性量化评价研究，而可注性量化评价是因素敏感性分析的基础，相关研究鲜有报道.敏感性分析方法可以分为局部敏感性分析以及全局敏感性分析.其中，局部敏感性分析只检验单因素变动对结果的影响程度，计算方便，但是分析往往需要一定假设，不能全面反应实际情况[28].而全局敏感性分析考虑了因素相互作用对结果的影响，更符合实际情况，在土木工程等多个领域应用广泛[29-31].其中，傅里叶幅度敏感性测试方法(FAST)即是典型全局敏感性分析方法.

将浆液扩散距离PSO-LSSVM预测值与测试集样本数据对比，评价扩散距离预测准确性.图5为测试集浆液扩散距离预测值与试验值对比.图6为浆液扩散距离预测值与试验值的拟合优度R2表现.

1 可注性室内试验

以P.O. 42.5R普通硅酸盐水泥为试验材料，以水泥浆液水灰比RWC、相对密实度Dr、细颗粒(直径<0.075 mm)含量θ、砂层特征粒径D10和D15为控制变量，开展129组砂样渗透注浆试验，试验测量记录浆液渗透扩散距离，以扩散距离定量表征可注性.

1.1 试验材料

1.1.1 普通硅酸盐水泥

例如，教学朱自清的《背影》一文，抓住“以‘背影’为线索表达深厚父爱”的方法，要求学生写一篇“母爱”的文章。有位学生这样写道：“曾经是那样温柔的手突然间给我的感觉却不柔软了，仔细一看，原来母亲的手已经结满了老茧。啊，这曾经抱起过我、喂养过我、搀扶过我的双手啊，在岁月的流逝中变化着，留下的不仅仅是皱纹，更是劳作的深深印痕啊！”

1.1.2 被注介质

目前胜利油田孤东采油厂共有污水处理站5座和1个污水沉降处理氧化塘，设计污水处理能力148 700 m3/d，实际处理污水142 300 m3/d，污水外输管线1.15 km，污水外调线33 km，各类污水外调泵10台。胜利油田孤东采油厂提出向质量要效益，围绕“实现更有质量、更有效益、更可持续发展”的工作目标[1]，实施低效污水外调泵（离心泵）节能技术改造项目，从而达到节能降耗的目[2-3]。

试验采用11种粒径配比砂样开展渗透性试验，每种砂样特征粒径如表1所示.

表1 砂样特征粒径

1.2 试验装置及试验方案

试验装置由氮气瓶、承压储浆桶、试验架3部分构成，承压储浆桶与氮气瓶相连，氮气瓶输出的空气压力转换为浆液压力，储浆桶顶盖上设置压力表监测注浆压力，压力表量程为0～3 MPa.试验架由上部顶盖、中部钢制承压管、下部底盘3部分构成.钢制承压管内部盛放待注浆砂样，砂样上方设置滤网，防止松散的砂颗粒移动，砂样下方设置透水石.砂样尺寸为标准试件尺寸，高度为10 cm，直径为5 cm.试验装置如图1所示.试验装置具体研发过程见文献[32].

图1 渗透注浆试验装置现场照片[32]

为系统研究砂层的可注性，在试验过程中充分考虑各个因素对砂层可注性的影响，除砂层粒径外，设定砂层相对密度Dr、细颗粒含量θ及浆液水灰比RWC为自变量.砂层相对密度Dr变化范围为0～100%；水灰比调节范围为0.8～1.6；细颗粒含量变化范围为0～16%.

EZH2高表达组乳腺癌患者组织中miR-200c mRNA表达水平较EZH2低表达组明显降低，差异有统计学意义(P＜0.05);转染siAFAP-EZH2后的乳腺癌细胞miR-200c mRNA表达水平明显高于control组和空白组(P＜0.05)。见表3。

渗透注浆主要有恒压力和恒流速两种施工工艺，可注性试验采用恒压注浆方式.注浆压力越大浆液扩散距离越大，然而过大注浆压力易于引起地层劈裂，破坏原状土体结构，在实际工程中常采用低压渗透注浆[1,16].砂层可注性试验中，为确保水泥浆液在砂样中充分扩散，试验中注浆压力控制为1.0 MPa.具体试验影响因素设置及试验结果见文献[32].

2 基于PSO-LSSVM的可注性预测模型

近年来，以神经网络(ANN)为代表的人工智能方法被广泛应用到可注性分类预测研究领域，推动了可注性理论进展[16-21].然而，神经网络方法具有过度拟合、泛化性能不高等缺点，最小二乘支持向量机(LSSVM)作为新一代机器学习算法，能较好解决小样本、非线性和高维问题求解，逐渐被应用于岩土工程问题分析中[22-25].此外，传统人工智能模型参数搜索常采用网格搜索和交叉验证方法，搜索效率及精度相对较低[26-27].而粒子群算法作为一种新型仿生进化算法，采用全局优化方法，可有效提高收敛速度及精度.

2.1 LSSVM回归原理

图3为训练集中浆液扩散距离PSO-LSSVM预测值和试验值对比.采用拟合优度R2为指标，定量评价基于PSO-LSSVM方法建立的可注性预测模型表现性能，即

yi=wφ(xi)+b.

(1)

式中：w为权向量；b为偏置量.xi、yi分别为系统输入向量和输出值.Suykens等[34]基于正则化理论，采用最小二乘成本函数和等式约束建立了LSSVM优化问题的最小化函数，其表达式为

(2)

约束条件

yi-wφ(xi)=b+ξi.

(3)

式中：C为惩罚因子，即拟合误差容忍度，C值越高，误差容忍度越小，越容易过拟合，C值越小，则容易欠拟合，合理取值可使所求的函数具有较好的泛化能力；ξi为松弛因子.

最小化函数的拉格朗日求解方程为

(4)

式中ai(i=1,2,…,l)为拉格朗日乘子.最优的参数a和b可以通过KKT条件获得.

要让传统的“景点旅游”转向“全域旅游”，需要构建基于地域实情特征多部门协作联合的社会合作管理机制体制为中心，以管理体制创新和环境建设提升为重要抓手，推动旅游行政管理向社会管理转变。

(5)

消去式(5)中的w和ξ，优化问题转化为求解如下方程

(6)

式中：I为l阶单位矩阵；Θ=[1,…,l]T；a=[a1,a2,…,al]T；y=[y1,y2,…,yl]T.K为核函数矩阵，其元素Kij=φ(xi)Tφ(xj)；i,j=1,2,…,l,其回归函数为

很多年以后，他像当日杀鼠一样，被判五刑加腰斩——劓刖、割舌、剁肢、笞杀同时执行之际便腰斩，最后慢慢碎尸。一家老小、三族亲戚、宾客门生……不分男女，一律斩首。七八个刽子手斧起刀落，也是一直忙到傍晚，这是一个雨夜。雨整整下了一个月。

(7)

LSSVM模型预测精度取决于核函数的参数取值.为提高预测精度，采用粒子群算法对其参数进行优化.

2.2 粒子群算法

粒子群优化算法(PSO)中，每个潜在解都被当成一个点或“粒子”，所有潜在解组成“粒子群”[35-36].任意一次迭代，粒子群基于单个粒子个体极值Pbest和群全局极值gbest来不断更新.群体中第i个粒子在n维空间的位置表示为xi=(xi1,xi2,…,xin)，其速度vi=(vi1,vi2,…,vin)，第i个粒子的个体极值Pbest=(Pi1,Pi2,…,Pin)，整个粒子群的全局极值gbest=(g1,g2,…,gn).在极值点处，通过方程(8)和(9)来更新自己的速度和位置：

vi(k+1)=qvi(k)+c1rand1(Pbest-xi(k))+

c2rand2(gbest-xi(k)),

(8)

xi(k+1)=xi(k)+vi(k+1).

(9)

式中：c1、c2为学习因子，c1、c2∈(0，2)；rand1和rand2为(0,1)之间的随机数；q为动量系数，随迭代计算更新.

2.3 PSO-LSSVM可注性预测模型建立

采用LSSVM方法建立砂层特征参数及注浆参数与浆液扩散距离之间的非线性映射关系.假设有n组训练样本数据(xi,yi)(i=1, 2,…,n)，在本模型中，任一组砂层可注性试验对应一个样本数据，其中xi为五维实数输入向量，分别包括水泥浆液水灰比RWC、砂层相对密实度Dr、细颗粒含量θ、砂层特征粒径D10和D15，yi表示该组试验测得的浆液扩散距离，以浆液扩散距离作为可注性量化评价指标.建模的过程即是寻找输入向量xi与输出值yi之间的非线性映射关系，关系模型示意图如图2所示.

以石英砂作为试验被注介质.所用石英砂中，二氧化硅(SiO2)质量分数大于96%，烧失量不超过0.40%，含泥量(包括可溶性盐类)不超过0.20%.

图2 基于LSSVM 建立的可注性预测关系模型示意

根据最小二乘支持向量机理论，相应的映射模型如式(7)所示.式(7)中，a和b可以通过解式(6)的线性方程组求出；yi为LSSVM模型的浆液扩散距离预测值.通过可注性试验获得的样本数据，对非线性映射模型进行训练.LSSVM模型核函数为RBF核，方程为

if (assertion==null) return new Model And View("/ssosync?url2=/home");

试验用水泥为42.5R普通硅酸盐水泥，水泥品质符合GB175—99《硅酸盐水泥、普通硅酸盐水泥》.水泥烧失量为0.56%.水泥颗粒粒径分布为0.4～80 μm，颗粒粒径分布范围相对较广，水泥颗粒特征粒径d85=23.872 μm，d90=28.93 μm，d95=36.127 μm.

高潮趋前一步，说，噢，原来是齐经理啊。高潮扭身指着田卓介绍道，这位是卓木文化传媒的田总。齐眉与田卓的手就握在了一起，高潮见她们客套得差不多了，又指着自己介绍说，《NEW商圈》主编高潮。齐眉伸出手来，和高潮热情地握了握，之后，把高潮和田卓领到写有他们名字的席位卡前，说，两位请坐。

K(xi,xk)=exp(-γ‖xi-xk‖2),γ>0.

(10)

式中γ为核函数参数，其值越小越容易欠拟合，值越大越容易过拟合.模型预测精度取决于C、γ的取值.根据文献[37]的结论，训练集样本数据占总样本数量的80%左右时，预测模型可得到最佳效果.本文在样本空间内均匀选取105组试验样本数据作为模型训练集，试验样本数据占样本总量81.4%.采用粒子群优化算法，对参数C、γ的取值进行优化.根据训练集试验样本数据，求得参数最优解为C=2.02、γ=1 854.41，以C、γ最优取值建立可注性影响参数与浆液扩散距离的关系模型.

通过对各组心肌样品检测，结果显示，附子提取物组、山茱萸提取物组、附子+山茱萸提取物组与模型组比较，ATP、ADP、肌酸、肌酐的含量均升高，其中，附子+山茱萸提取物组心肌样品中5种能量物质升高显著（P＜0.05、0.01）。结果见图3。

妈妈用实际行动证明着。这一年，她带我去重庆苦竹坝福利院认养了一个孤儿、我的妹妹巧玉。巧玉从福利院出来后，一直住在我家，三口之家变成了四口。之后的妈妈再也没考虑过婚事。

最小二乘支持向量机(LSSVM)是在SVM基础上用等式约束代替不等式约束，避免了二次回归问题，计算精度和效率更高[33].假设训练样本数据为{xi,yi}，(i=1,2,…,l)，xi∈Rn为n维系统输入向量，yi∈R为输出值.高维非线性映射φ：Rn→H，H为高维特征空间.在特征空间H中，拟合样本集为

(11)

图3 训练集中扩散距离预测值与试验值对比

R2值越接近1，说明关联度越好.图4为训练集扩散距离预测值与试验测定值之间拟合优度R2的表现.如图3,4所示，扩散距离预测值与模型值之间较为接近，拟合优度R2为0.962，模型拟合度较高.

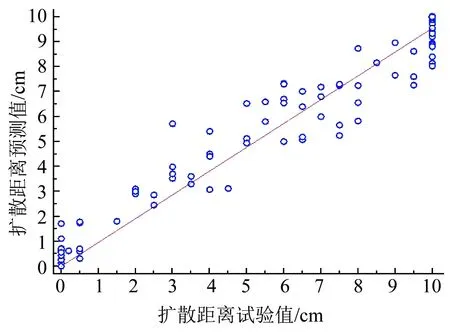
图4 训练集中扩散距离预测拟合优度R2

2.4 扩散距离预测准确性评价

本文将粒子群算法(PSO)和最小二乘支持向量机(LSSVM)相结合，通过粒子群算法搜索最佳的支持向量机参数，建立了浆液扩散距离预测的粒子群最小二乘支持向量机方法(PSO-LSSVM).以可注性室内试验测试结果作为模型训练和测试样本，建立了可注性PSO-LSSVM预测模型.基于PSO-LSSVM浆液扩散距离预测模型，采用FAST方法开展全局敏感性分析，得到了可注性影响因素敏感性分布.

图5 测试集中扩散距离预测值与试验值对比

图6 测试集中扩散距离预测值拟合优度R2

如图5,6所示，浆液扩散距离预测值与试验值较为接近，R2=0.982，说明所建立的PSO-LSSVM浆液扩散距离预测模型具有较好的泛化能力及良好的预测精度.本文为浆液扩散距离预测提供了有效方法，下一阶段将广泛开展不同注浆施工参数(包括注浆速率、注浆压力等)条件下的可注性试验，扩充试验训练样本，建立基于PSO-LSSVM方法的多种常用浆液的渗透扩散预测模型，并对其工程应用效果进行评价.

2.5 与现有方法对比

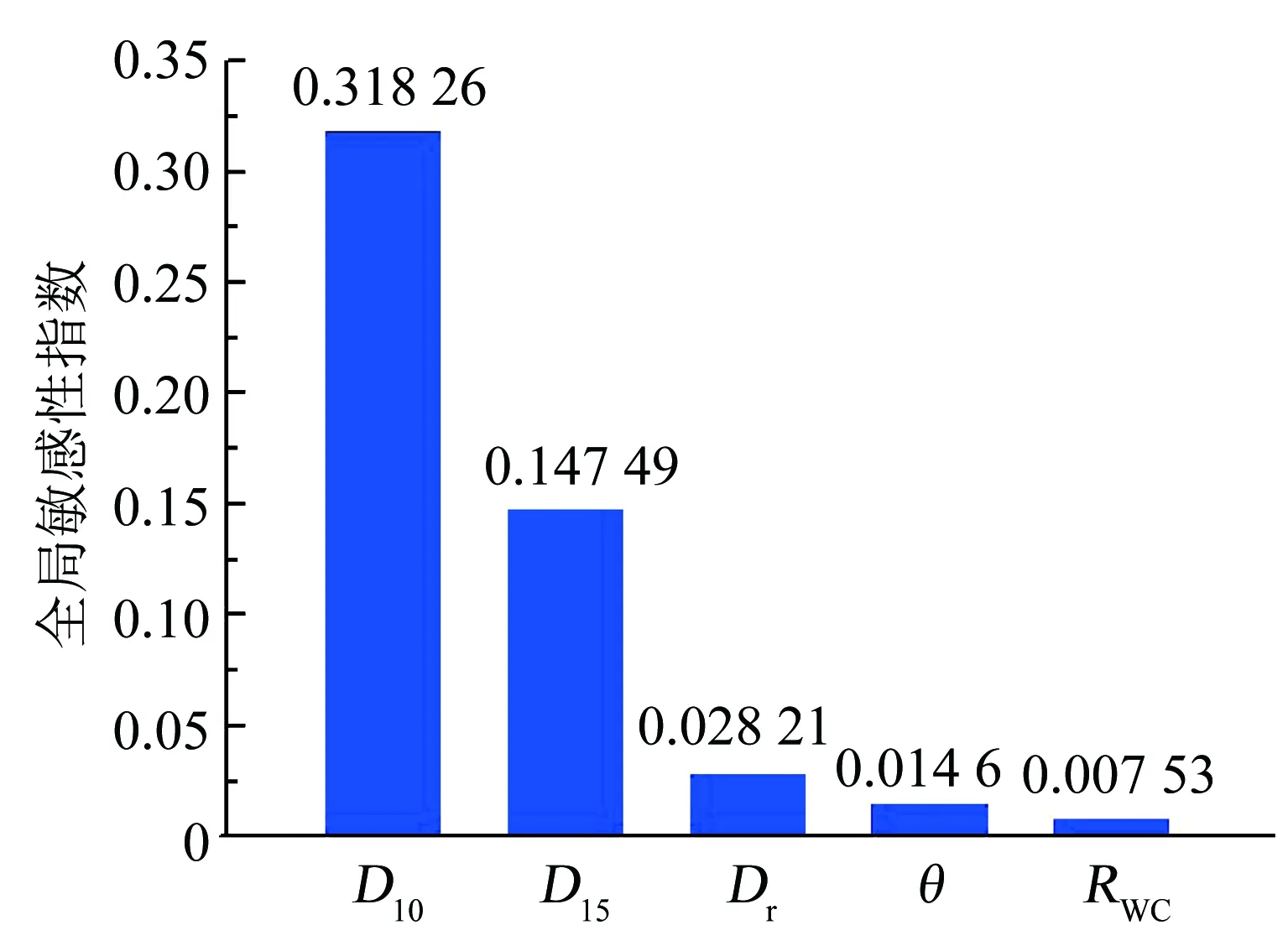
考虑柱形砂样中浆液扩散锋面起伏以及试验测量误差，认为浆液在砂样扩散距离L≤1 cm时，为不可注；1

Burwell模型和Incecik模型仅以被注砂层和水泥颗粒两者特征粒径比值作为可注性评判指标，在实际工程中应用较为广泛，可作为本文可注性预测对比方法.为保证所选取样本具有较好代表性，测试集样本数据均从样本空间中均匀选取，共计24组，约占总样本数18%.PSO-LSSVM的测试集样本可注性预测结果与经典Burwell模型和Incecik模型判定结果对比如表2所示.可以看出，PSO-LSSVM模型对24组测试集可注性结果进行了完全准确预测.Burwell模型对测试集中不可注样本和完全可注样本进行准确预测.然而由于模型自身限制，无法对不完全可注样本进行判识，或模型未定义，或判定为可注性样本，总体而言，该模型对样本可注性做出了过高的估计.

表2 可注性结果预测及对比

续表

与Burwell模型类似，Incecik模型对完全可注和不可注样本进行了准确估计，然而模型无法对注入不充分样本进行有效识别.此外，Burwell模型和Incecik模型预测结果不完全一致，不利于工程应用.总体而言，本文模型优于Burwell模型和Incecik模型，可注性预测精度更高，可为实际工程应用提供指导.

3 可注性影响因素全局敏感性分析

为评价影响因素对可注性敏感度，基于所建立的PSO-LSSVM浆液扩散距离预测模型，研究了各控制变量对可注性的敏感度，采用全局敏感性分析方法FAST，获得了可注性影响因素敏感性分布.

3.1 FAST方法简介

FAST方法是以方差分析为基础的灵敏性分析方法.通过对每个系统待分析参数分配一个特征频率值，求解傅里叶变换变量离散值的系统方程，计算与各参数频率相关的傅里叶系数，确定系统灵敏度[38-39].FAST方法可以在高维非线性系统参数发生较大变化情况下，进行有效分析计算.可注性影响因素全局灵敏性指数反映的是某个注浆参数变化对浆液渗透扩散距离的影响程度.全局灵敏度指数为

(12)

式中：Vi=V(E(y|Xi))，V(y)为总方差，SXi为参数Xi对模型输出总方差的贡献率.

社会上与学术界对于我国延迟退休年龄的政策议论不休，学者们各持己见，抒发了对该项政策利弊的分析。我国渐进式延迟退休年龄政策需要综合自身利弊以及国家发展环境来进行充分讨论，因此，更适合利用美国旧金山韦克里教授提出的事态分析法（又 称 SWOT，Strengths Weaknesses Opportunities Threat分析法）进行讨论，充分将我国延迟退休政策的优势（Strengths）、劣势（Weakness）、机会（Opportunities）以及威胁（Threats）进行论证。

3.2 敏感性分析结果

选取水泥浆液水灰比RWC、相对密实度Dr、细颗粒含量θ、砂层特征粒径D10和D15共5个参数，分析其对浆液扩散距离敏感性分布.假定各参数服从均匀分布，采用拉丁超立方抽样方法对参数抽样，抽样范围见表3所示.采用所建立的PSO-LSSVM预测模型计算样本浆液扩散距离，在此基础上，采用FAST方法计算参数敏感性指标.敏感性计算结果如图7所示.

表3 影响因素及其抽样范围

图7 影响因素敏感性指数分布

由图7可知，砂层可注性敏感性排序为D10>D15>Dr>θ>RWC，其中D10和D15敏感度远大于其他3个参数，影响最为显著.以Burwell模型[7]为代表的诸多传统可注性评判方法认为，当水泥浆液材料一定，砂层可注性取决于D10和D15，即认为D10和D15为除浆液材料之外的对可注性影响最为显著因素，这与本文敏感性分析结果较为一致.相比而言，砂层相对密实度Dr、细颗粒含量θ以及浆液水灰比RWC对可注性影响相对较小，因此，在实际可注性预测中，需尽量减少D10和D15参数量测的不确定性，从而为可注性的精确预测提供保证.

7个Ⅱ类海风锋个例的850 hPa层合成流场如图9b所示,内陆地区处于大陆东移高压控制之下,且呈现双中心结构:山东内陆为一较小高压中心,而长江口以南为另一更强高压中心。高压整体较强盛,为其所控制的区域带来较为稳定的天气形势。此时850 hPa沿海为自大陆向海面的风场,与图9a中1 000 hPa层上的海风反向,显示Ⅱ类海风环流较浅薄。而Ⅰ类海风锋的海风环流(图7)因副热带高压的整体势力,苏北及苏中的海风环流较深厚。

4 结 论

1)基于PSO-LSSVM方法建立的预测模型具有较高预测精度.浆液扩散距离预测值和试验测量值相近，拟合优度R2为0.982，可以准确预测样本完全可注、注入不充分以及完全不可注情况，而传统分类方法无法对注入不充分情况进行有效识别.

2)可注性影响因素敏感性排序为：砂层粒径D10>砂层粒径D15>相对密实度Dr>细颗粒含量θ>浆液水灰比RWC，其中D10和D15敏感性显著高于Dr、θ和RWC.

3)本文的研究也为渗透注浆扩散距离预测提供了新的思路，但还需广泛开展不同注浆参数(包括浆液类型、注浆速率、注浆压力等)条件下的渗透注浆试验，扩充训练样本，基于PSO-LSSVM方法建立适用范围更广的渗透注浆扩散预测模型，并对预测模型在工程中的应用效果进行评价.