基于自适应权重的RFID 室内定位算法

田 清，武 斌，王 丽

（天津城建大学 计算机与信息工程学院，天津 300384）

互联网的飞速发展使得位置信息服务的相关研究越来越多，全球定位系统（global positioning system，GPS）在室外环境定位中得到了广泛的应用，但在室内环境中没有定位信号，GPS 无法支持室内定位. 当前室内定位技术主要包括射频识别（radio frequency identification，RFID）[1]、蓝牙、超声波、全新无线网络数据通信技术（new wireless network data communication technology，ZigBee）[2]、无线局域网（wireless fidelity，WIFI）等技术.RFID 技术作为物联网发展的产物，因其成本低、部署方便、功耗低、通信速率高等优点[3]，已经应用在资产管理、防伪识别、医疗监护等众多领域[4].RFID定位系统主要由天线、阅读器、RFID 标签和定位算法组成[5].

RFID 室内定位中，由于室内环境的复杂多变容易造成标签的信号值不稳定，导致定位模型稳定性差，从而给定位算法的稳定性和误差带来影响.支持向量机（support vector machine，SVM）克服了神经网络存在的“过学习”和“多维灾难”等缺点，在处理小样本、非线性、多特征等问题上拥有明显的优势，当前已经有很多学者将支持向量机运用到了RFID 室内定位中.文献[6]提出了基于K-means 和SVM 的蓝牙室内定位算法，经过测试，该算法的定位精度稳定在1.5 m以内；文献[7]提出了基于支持向量回归和K 均值的RFID 室内定位方法，在2.25 m2的覆盖范围内，定位误差在17～31 cm 之间；文献[8]提出了基于核直接判别分析和支持向量机的定位算法，利用核直接判别分析去除RSS 信号噪声，通过提高样本质量来提高定位精度；文献[9]采用主成分分析提取定位特征，利用最小二乘支持向量机建立定位模型，并采用粒子群优化算法（particle swarm optimization，PSO）优化支持向量机的参数，定位精度和定位时间少于其他算法.当前关于RFID 室内定位算法的研究大多数是基于机器学习算法，并且都是依靠多样本进行研究，但在实际的RFID 室内定位中，由于复杂环境的影响，定位系统采集的样本数据误差较大，将误差较大的样本作为训练数据，所得预测模型就已经存在缺陷，从而影响预测模型的抗噪性能，最后对定位稳定性和误差带来影响.

为了让预测模型更好地适应室内复杂环境，提高预测模型的抗噪能力和泛化能力，本文根据误差分布特性采用马氏距离[10].改进加权最小二乘支持向量机（weighted least squares support vector machine，WLSSVM）算法的样本权重计算策略，自适应地给每个样本分配合适的权重，减小异常样本的权重；对WLS-SVM算法的惩罚系数和核函数参数建立目标函数，运用混沌粒子群优化算法（chaotic particle swarm optimization，CPSO）的全局渐进收敛、易跳出局部最优、收敛速度快的特点，快速建立定位模型.最后通过仿真验证了该算法的定位性能.

1 信号传播模型

室内环境的复杂多变，使得RFID 标签的接收信号强度（received signal strength indicator，RSSI）值不稳定，通常室内环境下信号传播路径模型采用的是大尺度信号衰减模型，该类模型所获取的RSSI 服从高斯分布，本文选取的信号传播模型为“对数正态阴影”模型[11]，该模型计算公式如下

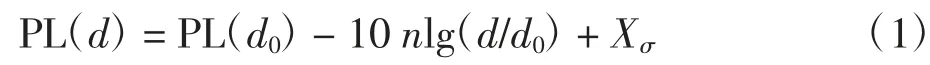
式中：PL（d）为电磁波传输d m 后阅读器的接收信号强度值，dBm；PL（d0）表示传播 d0m 后的值，其中 d0表示参考距离，且d0=1 m；n 表示路径损耗系数；d 表示阅读器与参考标签的距离；Xσ表示均值为0、方差为σ2的正态随机变量.

2 加权最小二乘支持向量机

WLS-SVM 以最小二乘支持向量机为基础，对误差向量 e = {ei}，i = 1，2，…，n 赋予误差变量 ei权重υi，得到相应的优化问题如下

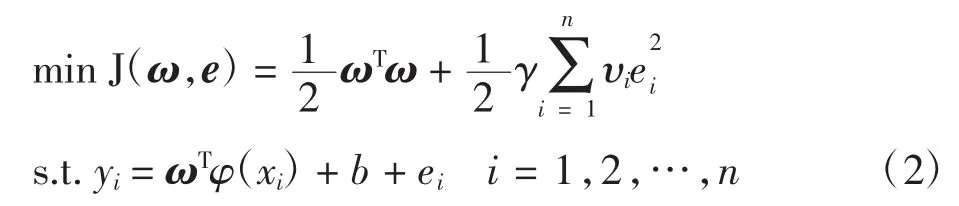
式中：ω 表示权向量；φ（·）表示将输入样本数据集映射到高维空间的映射函数；误差变量ei=αi/γ，γ 为惩罚系数且 γ ＞ 0，αi为拉格朗日乘子.

对公式（2）引入Lagrange 函数，将优化问题转换为对偶空间求解

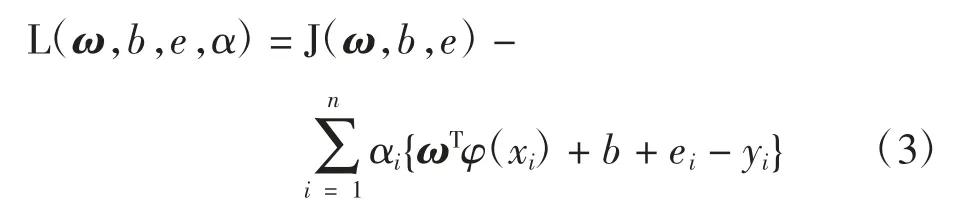
对公式（3）中各变量求取偏导数，可得以下线性方程组

最终的估计函数为

3 自适应权重的RFID 室内定位算法

本文利用马氏距离构造权重计算函数，有效地减小了异常样本对于训练模型的影响，并对WLS-SVM算法建立惩罚系数和核函数参数组合的目标函数，采用粒子群优化算法优化选择最优目标函数值，为了避免陷入局部最优，利用混沌粒子的随机性和遍历性，将混沌寻优的最优解代替粒子群寻优的最优解，得到最终的最优参数组合.

3.1 改进的WLS-SVM 权重计算方法

传统的WLS-SVM 算法的权重计算方法[12]为

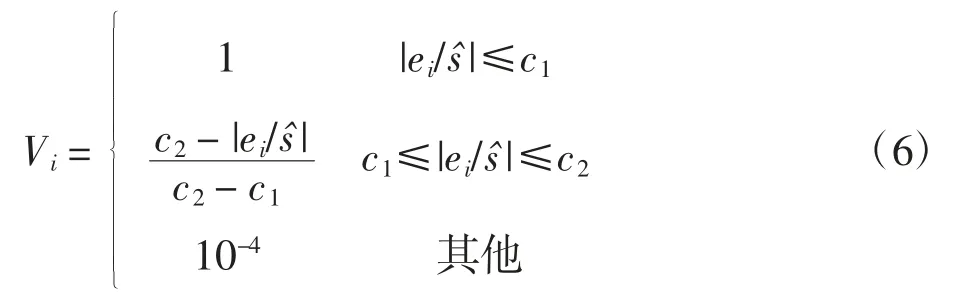
式中：c1=2.5；c2=3.0；sˆ表示误差变量鲁棒估计值.

传统的WLS-SVM 算法的权值为线性分布，异常样本对算法的模型影响较大，为了更好地适应室内复杂的环境，降低异常样本对模型的影响，本文提出如下自适应权重计算方法.

设误差向量e 的均值为μ，协方差矩阵为Σ，则误差变量ei与误差向量e 的马氏距离Mi为

设新的权重函数的判决门限为k，则

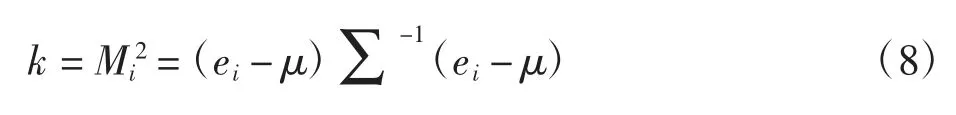
则新的权重函数表示如下

式中：k1，k2表示权重分布范围的宽度；s 表示误差变量ei的标准差.其计算公式如下

3.2 混沌粒子群优化算法（CPSO）

CPSO 根据混沌粒子的遍历性和随机性等特点，将混沌思想引入到PSO 中，寻优过程中将混沌粒子寻优的结果随机代替粒子群中任意一个粒子，使得粒子群进化速度加快，提高算法的进化速度.

本文选择Logistic 混沌系统[13]

式中：μ 为控制变量.

由初始值 Z0∈[0，1]可迭代出一个时间序列 Z1，Z2，Z3，….根据混沌粒子运动的特点，以PSO 寻优的最优位置为基础，将产生的混沌序列中的最优位置粒子替换当前粒子群中任意一个粒子的位置.

惯性权重ω 对算法的寻优能力有一定的控制能力，通常情况下ω 的调节方法如下

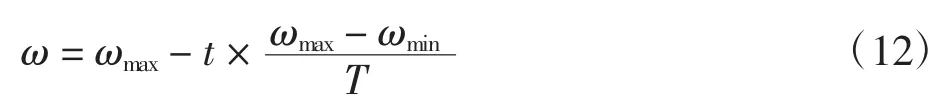
式中：ωmax表示初始惯性权重；ωmin表示终止惯性权重；t 为当前迭代次数；T 为最大迭代次数.

3.3 PSO-WLS-SVM

基于高斯核函数的WLS-SVM 算法中，参数γ 控制算法复杂度和误差，σ 值太大或太小会对样本数据造成过拟合或欠拟合现象.PSO 作为一种经典的优化算法，结构简单、操作性强、收敛速度快、求解精度高，通过在给定的解空间内进行最优解搜索，对核函数参数γ 和σ 的最优值进行自动搜索.PSO-WLS-SVM 算法采用粒子群算法优化传统的加权最小二乘支持向量机，算法主要步骤如下：

Step1：数据预处理，将样本数据进行归一化处理，4 个阅读器采集的信号强度值作为输入，RFID 标签的坐标作为输出.

Step2：根据WLS-SVM 模型计算样本误差ei，并根据公式（6）计算权重υi.

Step3：初始化每个粒子的位置和速度信息，主要包括粒子群搜索最大迭代次数Gmax、学习因子c1和c2、种群数目S、惯性权重ωmax和ωmin.

Step4：计算粒子的位置、速度、权重.

Step5：计算每个粒子的适应度值，确定最优位置Pbest，比较得到全局最优位置Pgbest.

Step6：如果满足适应度值条件或者达到最大迭代次数，寻优停止，输出当前最优解，否则返回Step4.

Step7：利用寻优得到最优的参数组合γ 和σ，得到最终的预测模型.

3.4 本文算法实现

PSO-WLS-SVM 算法采用粒子群算法优化传统的WLS-SVM，但是PSO 算法局部搜索能力较弱，容易陷入局部最优，进化后期收敛速度相对较慢，并且传统的WLS-SVM 算法的权重函数为线性分布，异常样本对算法的模型影响较大.因此本文采用混沌粒子群优化改进的WLS-SVM 算法，不仅提高了算法收敛速度，而且有效地提高了定位精度.

自适应权重的RFID 室内定位算法定义适应度函数为

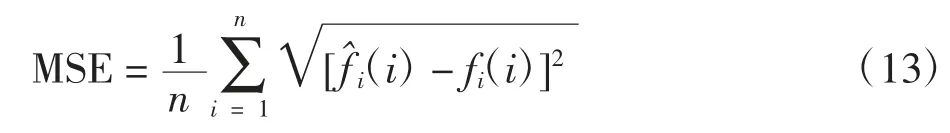
式中：MSE 表示均方误差；n 表示样本数量；fˆi（i）表示第i 个样本的预测值；fi（i）表示第i 个样本的真实值.

通过得到最佳的参数组合，使得MSE 最小

目标函数f 是惩罚系数γ 和核函数参数σ 的函数，利用CPSO 优化算法遍历寻找全局最优的参数组合，使得目标函数f 收敛到最小值.

本文提出的自适应权重的RFID 室内定位算法步骤如下：

Step1：数据预处理，将样本数据进行归一化处理，4 个阅读器采集的信号强度值作为输入，RFID 标签的坐标作为输出.

Step2：根据WLS-SVM 模型计算样本误差ei，并根据公式（9）计算权重υi.

Step3：权重更新，利用Step2 得到的权重υi重新计算每个样本的误差，再根据公式（9）重新计算权重定义权重平均变化量为

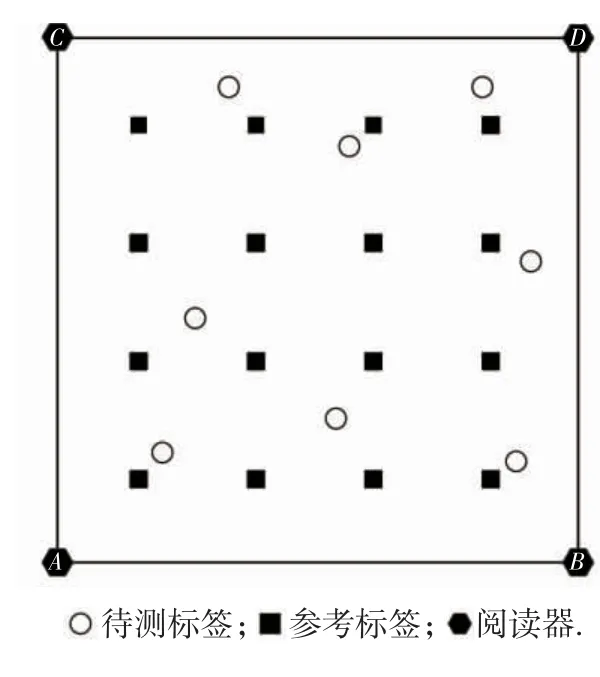
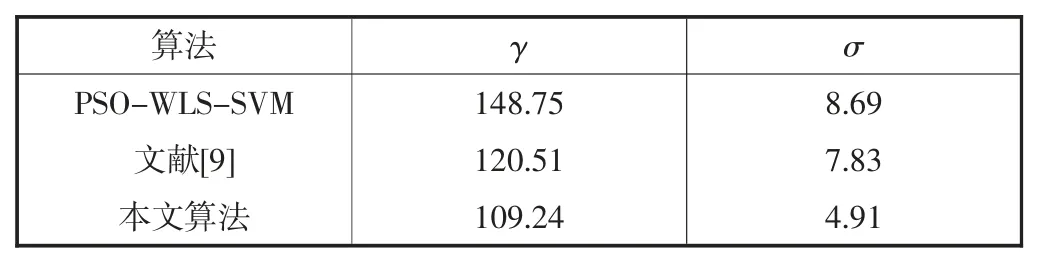
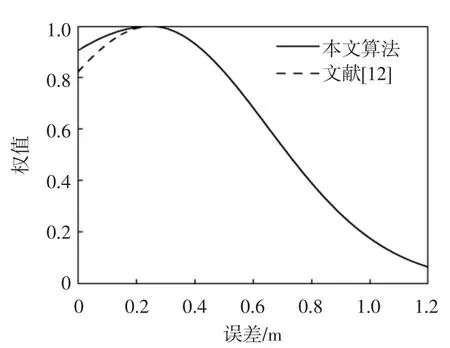
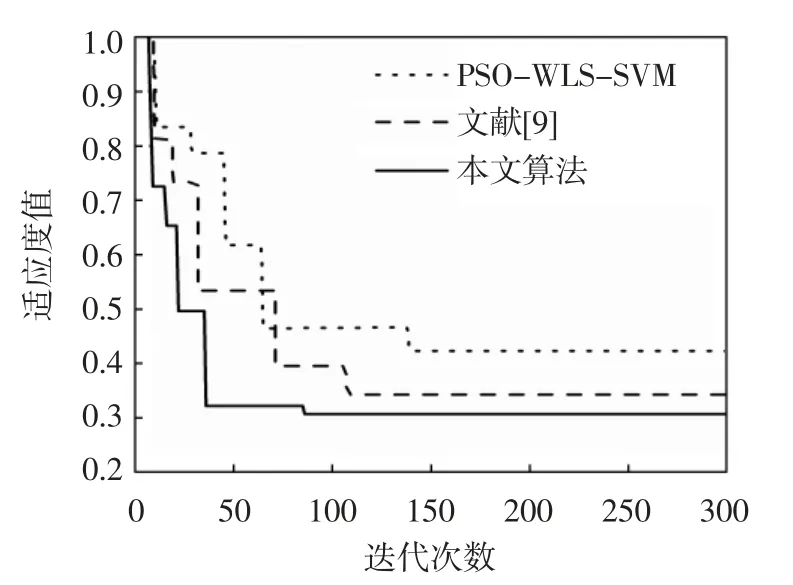
若Ve

Step4：初始化每个粒子的位置和速度信息，主要包括粒子群搜索最大迭代次数Gmax、学习因子c1和c2、种群数目S、混沌寻优最大迭代次数Gmax、惯性权重ωmax和 ωmin.

Step5：计算粒子的位置、速度、权重.

Step6：计算每个粒子的适应度值，确定最优位置Pbest，比较得到全局最优位置Pgbest.

Step7：利用混沌寻优对全局最优位置Pgbest进行优化，将 Pgbest=（Pg1，Pg2，…，PgD）映射到公式（11）的定义域[0，1]，其中Zi=（Pgi-ai）/（bi-ai），i=1，2，…，D.ai和bi分别对应γ 和σ 的定义域最小值和最大值，通过公式（10）计算产生混沌序列将混沌序列通过逆映射（m = 1，2，…）返回原解空间，得到可行解序列计算适应度值，替代当前个体最优值.

Step8：如果满足适应度值条件或者达到最大迭代次数，寻优停止，输出当前最优解，否则返回Step5.

Step9：利用寻优得到最优的参数组合γ 和σ，得到最终的预测模型.

4 仿真与分析

为了测试本文提出的定位算法的性能，仿真实验环境采用MATLAB2011b，计算机的硬件配置是处理器 i5、CPU 3.70 GHz、RAM 8 GB，操作系统为 WIN7 旗舰版.仿真区域大小为5 m×5 m 的平面，布置16 个参考标签和4 个阅读器. 4 个阅读器的位置坐标为：A（0，0），B（5，0），C（0，5），D（5，5）（见图 1）. 仿真实验根据公式（1）计算标签的RSSI 值，离线训练阶段将阅读器读取的参考标签RSSI 值和参考标签的真实坐标分别作为训练模型的输入和输出；在线预测阶段，根据阅读器读取待测标签的RSSI 值预测待测标签的坐标，并与待测标签的真实坐标进行对比，得出模型的预测结果，进行分析.

图1 实验场景图

4.1 参数选择

CPSO 优化算法参数设置如表1 所示.

表1 算法参数设置

采用RBF 作为核函数的WLS-SVM 算法，惩罚系数γ 和σ 核函数参数的选择至关重要.实验将PSOWLS-SVM、文献[9]的算法和本文算法进行对比分析，目标函数结果如表2 所示.

表2 不同算法的参数寻优组合

基于PSO-WLS-SVM 算法得到的目标函数最优解是γ=148.75，σ=8.69；文献[9]提出的算法得到的目标函数是γ = 120.51，σ = 7.83；本文提出的算法得到的目标函数最优解是γ=109.24，σ=4.91，分析可知：PSO 和CPSO 两种寻优算法能够找到更合理的WLSSVM 的参数，定位误差更小，但是因为PSO 容易陷入局部最优，而CPSO 利用混沌粒子很好地解决了局部最优问题，找到了更优的参数值，所以本文算法寻优效果更佳.

4.2 结果分析

图2 为本文算法和文献[12]算法的权重分布，从图2 可知，文献[12]算法的权重分布为正态分布，对于误差处于中间的样本所赋予的权重较大，而误差很小或者很大时，对应的样本权重相对很小，无法合理地设置权重，对于训练模型的质量有很大影响.因此，本文提出了自适应权重计算的方法，使得权重在对称轴两侧根据权重大小实现自由调整，使得误差大的样本权值相对较小，误差小的样本权值较大，与文献[12]提到的权值分布对比，本文提出的权值分布策略能够更有效地降低训练模型过程中异常样本对算法模型的影响，提高训练模型的质量，对模型预测提供很好的保障.

图2 权重分布

根据表1 算法初始化的参数设置，PSO-WLS-SVM算法、文献[9]算法和本文提出的算法的进化效果如图3 所示.从图 3 中可以看出，与 PSO-WLS-SVM 算法和文献[9]算法相比，本文提出的算法大约经过86 次迭代，就已经迭代完成，说明本文提出的算法相比于PSO-WLS-SVM 算法和文献[9]的算法收敛速度更快，定位耗时更短.

图3 不同算法迭代图

图4 所示为不同算法的误差累积概率分布.从图4 可知：当误差为0.5 m 时，WLS-SVM 算法的定位精度为45.5%，PSO-WLS-SVM 算法的定位精度为61.5%，文献[9]算法的定位精度为73%，本文算法的定位精度为90%；当误差为1.0 m 时，WLS-SVM 算法的精度为88.5%，PSO-WLS-SVM 算法的定位精度为97.5%，文献[9]算法的定位精度为98.5%，本文算法定位精度早已达到了100%.由此可知，本文提出的算法定位精度明显优于WLS-SVM、PSO-WLS-SVM 算法和文献[9]算法.

为了测试本文提出的RFID 室内定位算法的抗噪性能，仿真实验中在正常的训练样本中加入不同噪声样本比例模拟定位环境，随着噪声样本比例的增加，不同算法的定位精度有明显的变化（见图5）.如图5所示，对于传统的WLS-SVM 算法，噪声样本的比例超过10%时，算法的定位精度开始大幅度减小；当噪声样本的比例为 0～15%时，PSO-WLS-SVM 算法、文献[9]算法和本文算法的定位精度并没有太大的变化，噪声样本的比例超过20%时，PSO-WLS-SVM 算法和文献[9]算法的定位精度开始大幅度减小；当噪声样本的比例超过30%时，本文算法的定位精度才开始大幅度减小，因此本文算法的抗噪性能更好，定位更稳定.

5 结 语

本文针对复杂环境下室内定位稳定性差和误差大的问题，提出了一种基于自适应权重的RFID 室内定位算法，通过自适应权重解决样本数据对预测模型的影响.仿真实验结果表明，本文提出的定位算法在室内定位中表现出了良好的定位精度和稳定性，具有良好的应用前景.