基于机载LiDAR数据估测林分平均高
赵 勋,岳彩荣*,李春干,张丽梅,谷 雷
(1. 西南林业大学林学院,云南 昆明 650224;2. 广西大学林学院,广西 南宁 530004;3. 西南林业大学园林园艺学院,云南 昆明 650224)
林分平均高是评价森林生产力、计算森林生物量和蓄积量、研究森林碳循环的重要参考指标[1-3]。传统的森林参数调查中,需要花费大量人力物力,在地形复杂、人迹罕至的地方,甚至无法实现人工地面调查。
20世纪80年代中期,激光雷达技术被应用于森林参数的获取[4]。机载LiDAR技术由于其具有测量精度高、实时性好、方便灵活等特点被广泛用于森林参数的获取。利用机载LiDAR点云数据获取森林参数可根据点云密度大小分为两类:即利用高密度点云直接获取单木参数,包括单木树高、冠幅、冠面积和材积等[5-7]。这一类方法往往需要高密度的激光点云,通常点云密度需达15点·m-2以上,数据获取成本较高,大区域范围难以应用。另一类利用相对稀疏的点云密度获取林分测树因子,如平均高、郁闭度、蓄积量等林分因子。通过建立机载LiDAR点云数据的统计特征和野外样地的林分调查因子的相关模型完成大范围的森林参数制图[8-9]。这一类方法对机载LiDAR点云数据密度要求较低,通常利用2点·m-2以上的低密度LiDAR点云即可与样地统计数据建立模型,完成大区域下森林参数的获取[10-12]。
近年来,已有大量研究利用机载LiDAR点云数据结合样地调查数据建立模型估测林分参数。这些模型主要分为参数模型和非参数模型。参数模型以线性回归为代表,Næsset、穆喜云、庞勇等[1,4,13]分别对挪威东南部的针叶林、内蒙古大兴安岭生态站典型的森林类型、山东省泰安市徂徕山林场人工林为主的林分利用机载LiDAR点云数据建立线性回归模型估测林分平均高都得到了较好的结果。Kwak、Silva、刘浩、徐婷等[14-17]基于机载LiDAR点云数据采用线性回归建立模型估测生物量、蓄积量、平均胸径、胸高断面积等森林参数也都取得了较好的效果。然而,虽然线性回归模型简单明了,但以此建立模型对数据要求较高,它假设数据满足正态性、方差齐性、独立性和线性相关等严苛的条件才能建立模型[18],实际应用中数据并非能满足以上的条件。非参数模型主要有支持向量机、随机森林、K近邻法(K-NN)、人工神经网络(ANN)、决策树等,这些方法都已被成功应用于森林参数估测[19-21]。鲁林等[22]基于机载LiDAR点云数据探索了随机森林算法在估测林分平均高中的适用性。Alberto等[23]基于机载LiDAR点云数据构建K近邻回归模型对位于巴西的火炬松(Pinus taedaL.)种植园进行了林分平均高和优势高估测,模型的相关性(R2)分别为94%和90%。Monnet等[24]基于机载LiDAR点云数据构建支持向量机和普通最小二乘模型对林分优势高进行估计,结果显示支持向量机和普通最小二乘估测精度相近,但支持向量机模型精度更高。Tompalski等[25]利用最小二乘模型、随机森林、K-NN 3个模型测试模型的可移植性,基于不同区域、不同点云特征对断面积加权平均高、断面积平均木直径和总材积进行估测,显示了机器学习算法在森林参数估测上具有巨大的优势性。洪奕丰等[26]基于机载LiDAR点云数据对长白落叶松(Larix olgensisHenry.)组分生物量使用随机森林算法反演建模,随机森林模型的精度(R2)均高于0.91。由于机载LiDAR点云数据的特殊性,能从三维结构上反映森林的垂直结构,因此,机载LiDAR点云数据可提供更多描绘森林的特征来估测森林参数。对于多特征参数的应用,更好的挖掘机载LiDAR点云数据获取森林参数的潜力,无疑机器学习提供了更加便利的技术手段。
国外已有多位研究者基于机载LiDAR点云数据使用不同的机器学习方法对森林参数进行了估测研究,而国内相应研究较少。鉴于此,本研究以广西壮族自治区高峰林场试验区为研究区,采用2016年9月获取的机载LiDAR点云数据为基础,结合105块同步获取的样地数据,使用随机森林、支持向量机、支持向量机+随机森林的组合模型分别对研究区林分平均高进行建模估测。评价不同方法在使用机载LiDAR点云数据估测林分平均高应用中的适应性,采用模型精度高、泛化能力强的模型完成研究区林分平均高制图。
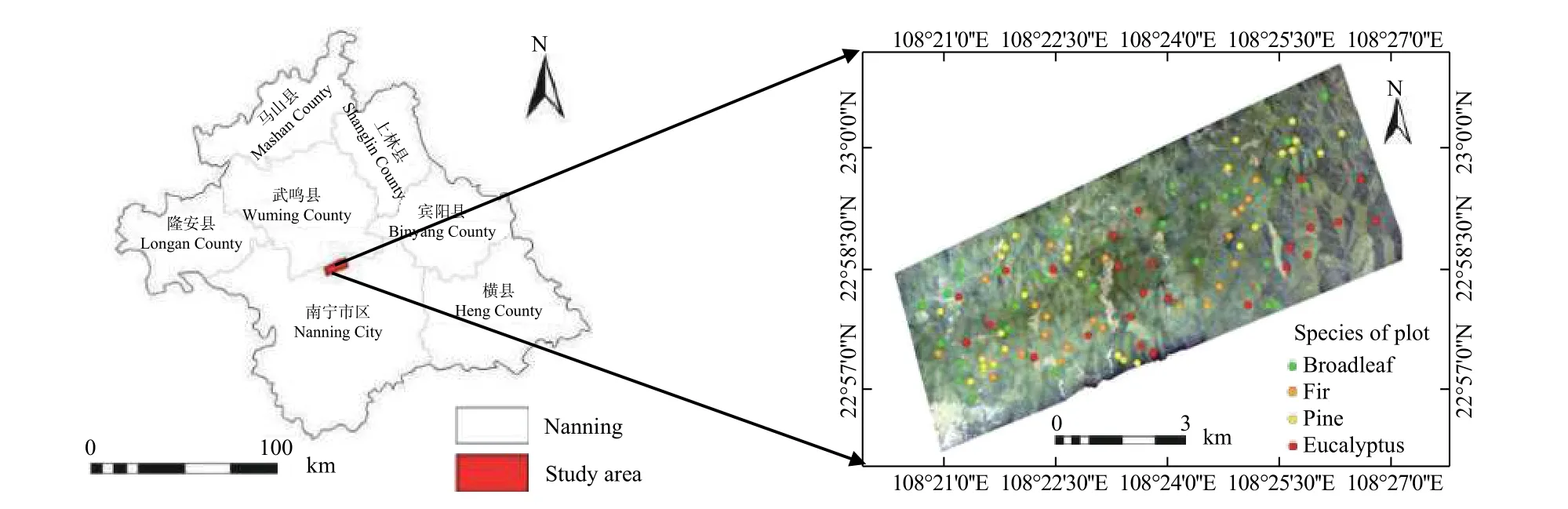
图1 研究区位置图Fig. 1 The location map of study area
1 数据与方法
1.1 研究区概况
试验区位于广西壮族自治区南宁市北部的国有高峰林场内,为一个呈东北-西南走向的近矩形区域,中心地理位置为108°23′45″ E, 22°58′33″ N,长11.2 km,宽4.2 km,面积约为4 770 hm2。研究区位置见图1。研究区属低山地貌,海拔90~460 m,地形封闭,一般坡度为24°~34°,坡度大于24°的面积占研究区面积的75%。属亚热带季风气候,年均温度21.6°左右,年均降水量1 300 mm,相对温度79%,热量充足,雨水充沛,林木生长迅速。森林覆盖率为90%以上,人工林约为95%,除桉树外,年龄大多在15 a以上,主要树种有尾叶桉(Eucalyptus urohpyllaS.T. Blake)、巨尾桉(Eucalyptus grandis×E. urohpylla)、马 尾 松(Pinus massonianaLamb.)、 湿 地 松 (Pinus elliottiiEngelmann)、八角(lllicium verumHook. f.)、红椎(Castanopsis hystrixMiq.)、火力楠 (Michelia macclureiDandy)、米老排(Mytilaria laosensisLec.)、厚荚相思(Acacia crassicarpaBenth.)等。60%的林分为人工天然混交林,在沟谷内有少量天然杂木。
1.2 样地数据获取
研究区划分为4个优势树种组,分别设置22块杉木样地、25块桉树样地(尾叶桉、巨尾桉)、29块松树样地(马尾松、湿地松、杂交松)、29块一般阔叶树样地(红椎、火力楠、米老排、八角、厚荚相思和天然杂木林),共计105块样地。在GIS软件中,基于小班空间分布图上根据优势树种(组)分布按照相对均匀分布的原则随机布设样地,确定样地中心点的图面坐标,根据图面坐标采用手持双频差分GPS导航至样地中心,观察周围林分情况,若该中心四周30 m内林分均属于同一类型,则该中心即为样地中心,否则,移动该中心至合适位置。如果无论怎样移动样地中心,样地都无法只包含一个林分类型,可包含两个类型,但不能包含无林地。最后在样地中心西北方向20 m处附近,随机确定样地西北角点,用森林罗盘仪和激光测距仪测设样地边界,样地面积为30 m×30 m。样地分布位置图见图1。在测设的样地内每木检尺,用胸径尺测量胸高直径,起测胸高直径为5 cm。用超声波测高仪(Haglóf VERTEXⅣ)测定3株平均木高和1株优势木高。样地计算指标包括:平均直径、平均树高、断面积、每公顷株数、每公顷蓄积量,其中每公顷蓄积量计算根据断面积和平均高采用形高表计算。林分平均高采用断面积加权法计算,计算公式为式(1)。以此方法完成105块样地调查。

式(1)中:H为林分平均高,hi为第i株树木的林木高度,gi为第i株树木的胸高断面积,n为林分株数。
1.3 机载LiDAR数据获取及处理
2016年9月使用R44直升机搭载奥地利RIEGL公司的VUX-1LR激光雷达系统获取整个研究区数据,飞行覆盖范围108°20′9″~108°27′33″ E,23°0′28″~22°56′3″ N。飞行总覆盖面积约为55 Km2,共飞行3驾次,每次约为5 h。该系统集激光测距、全球定位系统(GPS)和惯性导航系统(IMS)于一体。激光器工作波长为1 550 nm,激光束发散角为0.5 mrad,获得的平均点云密度约为2点每m2。
首先对机载LiDAR数据进行预处理,预处理包括去噪、滤波、分类。本研究选用阈值法消除噪点,使用不规则三角格网滤波算法[27],完成整个研究区的地面点和非地面点分类;由于森林地形的复杂性,目前很难有一种普适性的地面滤波算法可以科学准确的分类出地面点。因此由此方法得到的地面点需进一步目视解译,人工修正一些未分类正确的点,最终准确得到整个研究区的地面点。对于非地面点部分,研究区位于森林,所以只将非地面点区分为植被点和其他点,其他点不做处理。最后利用植被点与基于地面点插值生成的数字地面模型(DEM)作差得到整个研究区归一化后的植被点云。
利用归一化的植被点云提取相关点云特征统计量。具体包括:高度百分位数13个(H5,H10,H20,H25,H30,H40,H50,H60,H70,H75,H80,H90,H95)、密度变量10个(D0,D1,D2,D3,D4,D5,D6,D7,D8,D9)、变异系数(Hcv)、最大值(Hmax)、最小值(Hmin)、平均值(Hmean)、中位数(Hmedian)、标准差(Hstd)、方差(Hvar)、高度百分位数四分位数间距(Hiq)等8个高度变量。由于LiDAR点云的首次回波对树冠表面探测更为敏感,因此本次研究使用首次回波提取以上LiDAR特征。为了便于地面样地数据匹配,统计空间林分尺度设置为30 m×30 m。
1.4 建模方法
基于LiDAR点云数据获取的31个特征变量结合实测样地数据采用随机森林、支持向量机回归及两种方法的组合回归建模。其中,组合回归建模利用随机森林优选特征,最后利用优选特征进行支持向量机回归建模。首先将105块样地数据按照3:1的比例随机划分为79个训练样本数据,26个检验样本数据,以79个训练样本数据作为建立模型的基础数据。其次利用格网搜索算法与十折交叉验证方法寻找最优参数,完成模型的建立。最后采用26个检验样本数据检验模型,完成模型的精度评价。精度评价主要采用决定系数(R2),均方根误差(RMSE)对比随机森林、支持向量机回归及两种方法的组合模型在机载LiDAR点云数据估测林分平均高中的适应性。以上回归模型建立均使用python语言实现。
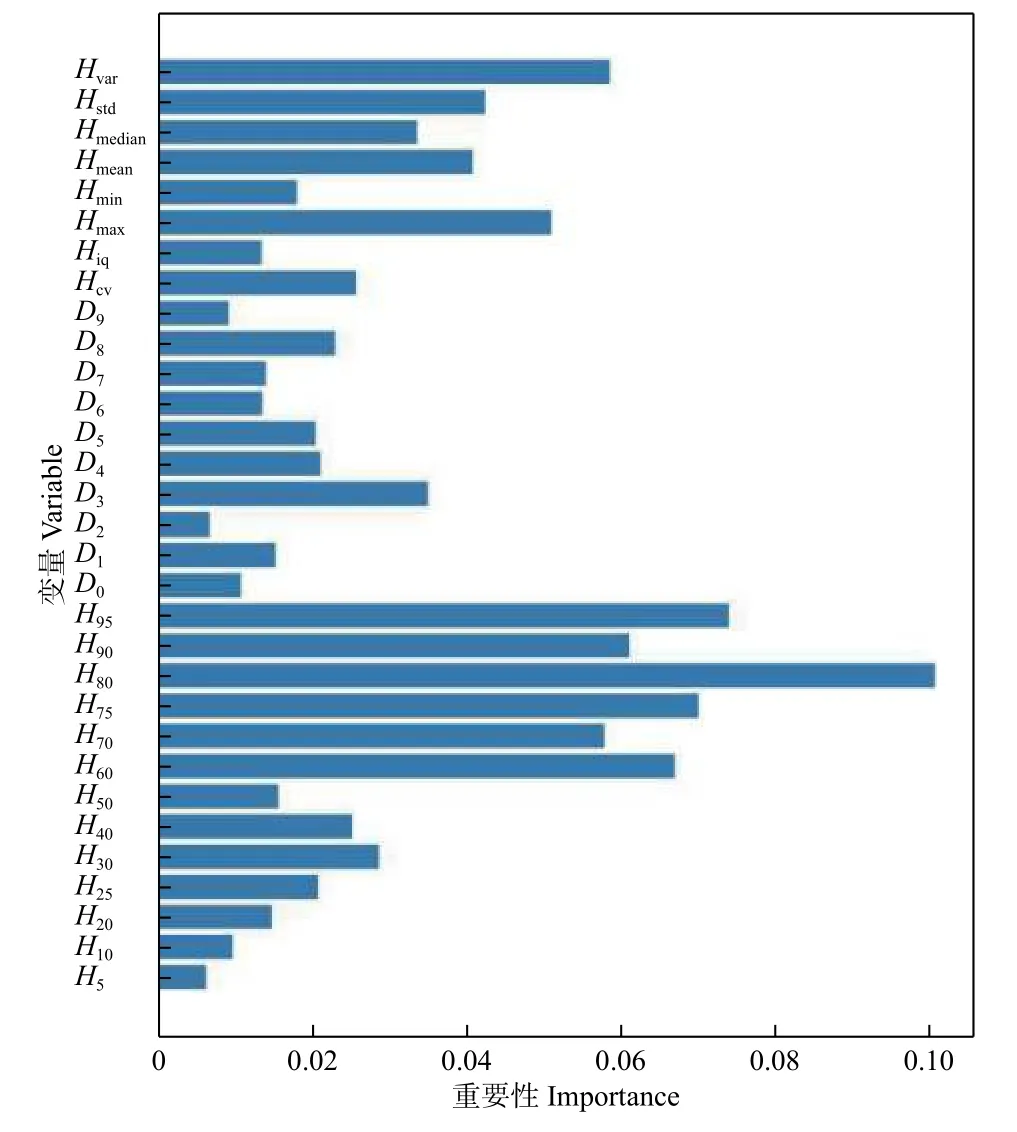
图2 特征变量重要性Fig. 2 Importance of characteristic variables

表1 随机森林模型特征优选Table 1 RF model feature selection
2 结果与讨论
2.1 结果
2.1.1 模型建立 基于79个训练样本数据与机载LiDAR数据提取的30 m×30 m空间林分尺度下的特征变量回归建模。使用网格搜索算法结合十折交叉验证方法分别对随机森林、支持向量机及组合回归模型进行参数寻优。(1)随机森林主要对构建决策树的数量,使树节点分裂的最小特征数,最小叶子节点3个参数进行寻优。最终参数最优解的结果为:构建决策树的数量75,树节点分裂的最小特征数为2,最小叶子节点为2;(2)支持向量机模型参数寻优中选用常用的3个核函数,即线性核、RBF和多项式核函数分别进行。寻优结果为:核函数为RBF,惩罚参数(C)为10,gamma参数为0.02。(3)根据参数寻优建立的随机森林回归模型得到参与建模LiDAR特征变量的重要性,如图2。图中重要性值越高,该特征对林分平均高估测越重要。由图2可以看出,LiDAR特征变量中几个高度分位数的重要性值都较大,其中以H80高度分为数最大;其次为点云的几个统计变量(Hvar、Hmean、Hstd等)。说明植被点云的首次回波中75%~95%的高度分位数或最大高度分位数(Hmax)有利于拟合林分平均高或优势木平均高,这与前人研究结果一致[22,28-30]。密度变量重要性值较大的有D3,D4,D8等。其中D3被选中与刘浩等[17]的研究结果一致。研究中选择大于80%信息累计贡献的特征变量使用支持向量机回归建模,随机森林回归模型优选后的特征变量具体见表1。依据网格参数寻优方法,进一步得到组合模型的参数最优解:核函数为RBF,惩罚参数(C)为10,gamma参数为0.01。
2.1.2 模型效果 使用79个训练样本数据和26个检验样本数据分别利用3个回归模型进行林分平均高预测,进一步分析3个模型的预测林分平均高和实测林分平均高的相关关系。图3、4、5分别为随机森林模型、支持向量机模型以及两种方法组合模型的预测林分平均高和实测平均高的相关关系。

图3 随机森林回归模型预测林分平均高和实测平均高对比图Fig. 3 Comparison of stand mean height between and the RFR model estimations the ground measured values
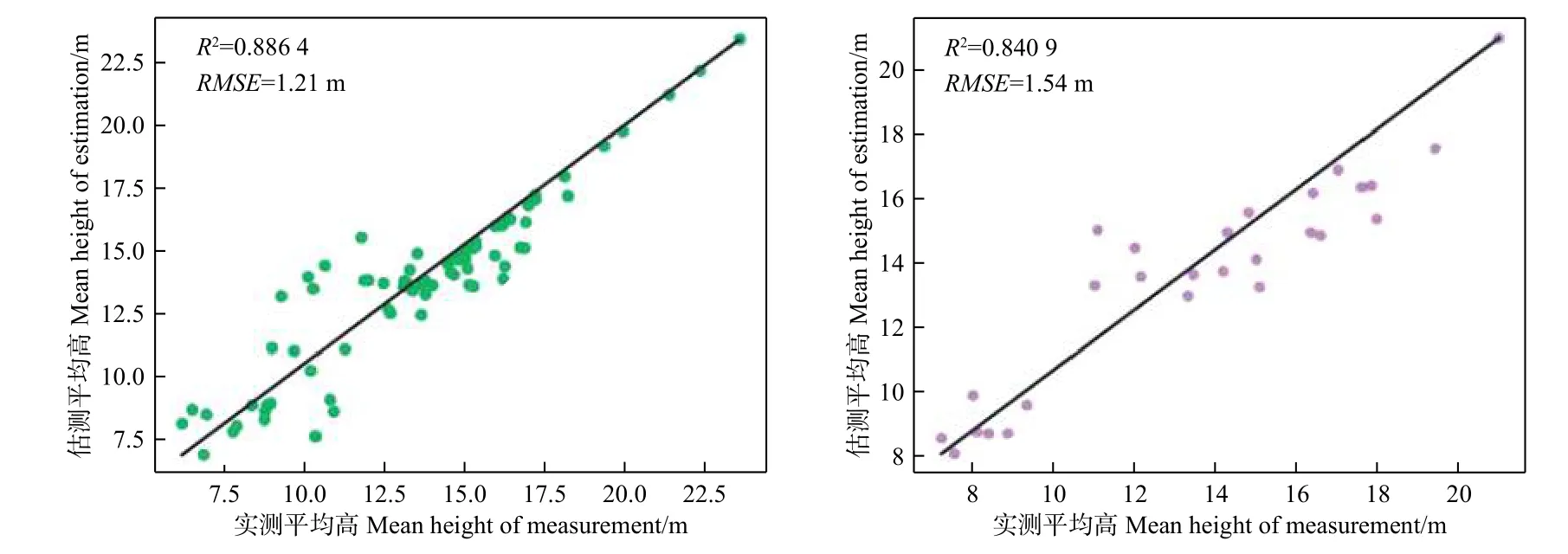
图4 支持向量机回归模型预测林分平均高和实测平均高对比图Fig. 4 Comparison of stand mean height between and the SVR model estimations the ground measured values
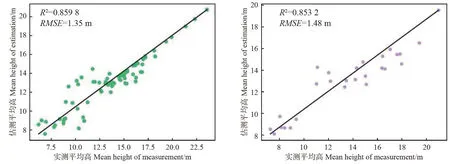
图5 组合回归模型预测林分平均高和实测平均高对比图Fig. 5 Comparison of stand mean height between and the RFR&SVR model estimations the ground measured values
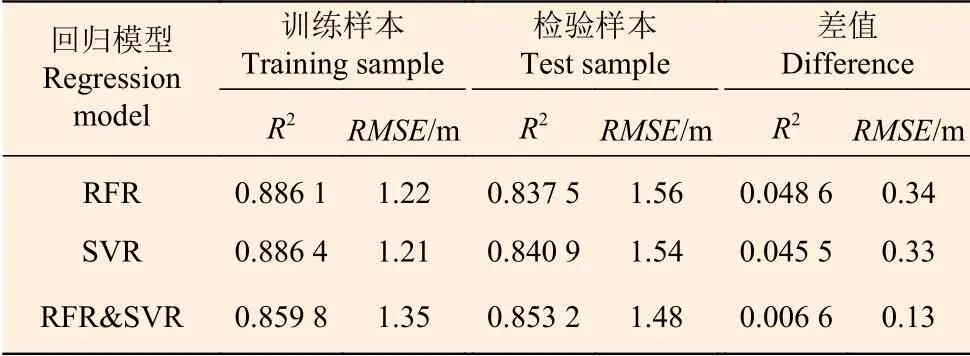
表2 模型精度评价指标Table 2 Model accuracy evaluation index
3个模型精度评价指标见表2。表中差值一项反映了3个模型中训练数据和检验数据对应的精度指标之差,差值越小,模型泛化能力越强。由表2可知,3个模型的决定系数(R2)均大于0.85,RMSE也都较小。从检验样本的精度指标及其与模型精度的差值看,组合模型(RFR&SVR)的差值最小,泛化能力最强,说明利用组合模型更适合推演到区域尺度完成林分平均高制图。最后,采用python语言读取整个研究区的对应的LiDAR变量特征,利用组合模型完成整个研究区林分平均高制图,图6为研究区林分平均高分布图。

图6 组合模型(RFR&SVR)林分平均高制图Fig. 6 Stand mean height map based on combined model (RFR&SVR)
2.2 讨论
(1)随机森林回归模型中,从训练样本的随机抽样到特征选择的随机抽样,两层随机抽样保证了模型的稳定性,在预测林分平均高中具有较强的抗噪声能力,使得随机森林模型在预测林分平均高中表现较好,训练数据和检验数据的预测精度均高于80%。同时,每棵决策树的建立,投票选择出对林分平均高解释性最强的特征变量,取每个特征的均值作为最终在模型中的贡献程度,相比于支持向量机模型而言可以更好的解释特征变量。
(2)使用支持向量机预测林分平均高,通过核函数由低维到高维映射,解决了高维空间计算复杂的问题。同时,支持向量机寻找最少的支持向量构建支撑面,对噪声异值敏感度降低。回归过程中引入误差损失函数,使得误差容忍度提高,模型精度有所提高。对于小样本数据,支持向量机表现较优,研究结果也证明了这一点。较随机森林而言,支持向量机在利用105块实测样地数据建模预测林分平均高中精度优于随机森林模型。
(3)组合模型利用了随机森林模型优选特征的可解释性和科学性,同时结合了支持向量机模型对小样本数据回归预测的优势,更好的完成林分平均树高的预测。研究结果得到组合模型的泛化能力最强,估测精度也与前两种方法相差较小,更适合于模型的推演与制图。
(4)随机森林和支持向量机这一类机器学习算法,在模型的构建中,模型参数的优化是精确的预测林分平均高的关键。使用格网搜索算法进行参数的选择,是一种高效快捷的方式,它利用交叉验证的方法对每一组参数进行打分,最终选取出最优的参数组合,避免了在预测林分平均高建模中盲目调节参数的目的。
(5)利用105块实测数据对研究区内的林分平均高建模回归预测,虽然取得了较好的结果,但由于本次研究中受样地数量的限制,没有分树种进行估测,一定程度会影响树高的估测精度。因此,后期需要分树种建模预测林分平均高,进一步改善预测精度。
3 结论
基于LiDAR点云数据提取的31个特征变量,以105块样地数据为基础,使用随机森林、支持向量机、两种方法的组合模型对广西壮族自治区高峰林场实验区的林分平均高进行预测。3种模型的模型精度和检验精度都较高。其中随机森林模型的决定系数(R2)和均方根误差(RMSE)为0.886 1和1.22,独立样本检验结果R2和RMSE为0.837 5和1.56;支持向量机模型的决定系数(R2)和均方根误差(RMSE)分别为0.886 4和1.21,独立样本检验结果R2和RMSE分别为0.840 9和1.54;两种方法的组合模型的决定系数(R2)和均方根误差(RMSE)分别为0.859 8和1.35,独立样本检验结果R2和RMSE分别为0.853 2和1.48。总体上组合模型在基于机载LiDAR点云数据估测林分平均高中模型泛化能力最强、制图精度最高,更适合研究区完成森林林分平均高制图。
由于本次研究区仅限于高峰林场,研究范围有限,研究中的3种估测方法及其效果差异是否适用广西其它地区还有待进一步试验。基于机载LiDAR点云数据开展可移植性的森林参数估测方法是今后深入研究的重要内容,也是笔者今后努力的方向。
致谢:本次实验的机载LiDAR点云数据及野外调查地面数据由广西省壮族自治区林业勘测设计院提供,在此表示衷心感谢。

