构造函数 破解大小比较*
广东省广州市第十六中学(510080) 温伙其
导数在研究函数中的应用是近年高考命题的一个热点考向.利用导数解决大小比较,关键是构造与待证不等式紧密联系的函数,然后以导数为工具来研究该函数的单调性、极值、最值(值域).本文探究如何构造函数解决抽象函数不等式;解决同构式不等式;解决距离最值;处理双极值点问题;处理极值点偏移问题.
一、构造函数解决抽象函数不等式
构造函数解抽象函数不等式,其本质是用导数研究对应函数单调性,而对应函数需要构造,通过对问题的条件和结论进行类比、联想、抽象、概括,准确构造出符合题意的函数.一般是对u±v,u·v,导函数形式的化归处理,当导函数形式出现的是“+”时,优先考虑u·v型,当导函数形式出现的是“-”时,优先考虑型,然后利用函数的单调性、奇偶性和数形结合求解即可.
例1已知函数f′(x) 是函数f(x) 的导函数,f(1)=(其中e为自然对数的底数),对任意实数x,都有f′(x)>f(x),则不等式2f(x)<ex+1的解集为( )
A.(-∞,1) B.(1,+∞) C.(1,e) D.(e,+∞)
解析由题意构造函数g(x)=-1,则g′(x)=>0,故g(x) 在R 上递增,而g(1)=-1=0,不等式2f(x)<ex+1可化为-1<0,即g(x)<g(1),解得x<1,不等式2f(x)<ex+1的解集为(-∞,1),故选A.
小结常见的抽象形式及对应构造的辅助函数:
(1)条件含有xf′(x)+f(x)结构形式,一般构造新函数F(x)=xf(x);
(2)条件含有xf′(x)-f(x)结构形式,一般构造新函数F(x)=
(3)条件含有f′(x)+f(x)结构形式,一般构造新函数F(x)=exf(x);
(4)条件含有f′(x)-f(x)结构形式,一般构造新函数F(x)=
(5)条件含有nf(x)+xf′(x)结构形式,一般构造新函数F(x)=xnf(x);____
(6)条件含有nf(x)-xf′(x)结构形式,一般构造新函数F(x)=
(7)条件含有f′(x)sinx+f(x)cosx结构形式,一般构造新函数F(x)=f(x)sinx;
(8)条件含有f′(x)sinx-f(x)cosx结构形式,一般构造新函数F(x)=
(9)条件含有f′(x)cosx-f(x)sinx结构形式,一般构造新函数F(x)=f(x)cosx;
(10)条件含有f′(x)cosx+f(x)sinx结构形式,一般构造新函数F(x)=
二、构造函数解决同构式不等式
同构式不等式是指除了变量不同,其余地方均相同的不等式.既然同构式不等式两侧呈现同构特征,则可将相同的结构构造为一个新函数,进而结合该函数的单调性等性质,可比较大小或解不等式.
例2(2014年高考湖南卷文科第9 题) 若0<x1<x2<1,则( )
A.ex2-ex1>lnx2-lnx1B.ex1-ex2>lnx2-lnx1
C.x2ex1>x1ex2D.x2ex1<x1ex2
解析A 选项:ex2-ex1>lnx2-lnx1⇔ex2-lnx2>ex1-lnx1,构造函数f(x)=ex-lnx,则f′(x)=再构造函数g(x)=xex-1,则有g′(x)=(x+1)ex>0 恒成立,所以g(x)在(0,1)单调递增,而g(0)=-1<0,g(1)=e-1>0,因此存在x0∈(0,1),使得g(x0)=0,由单调性可判断出:x∈(0,x0),g′(x)<0⇒f′(x)<0,x ∈(x0,1),g′(x)>0⇒f′(x)>0,所以f(x)在(0,1)不单调,不等式不会恒成立;
B 选项:ex1-ex2>lnx2-lnx1⇔ex1+lnx1>ex2+lnx2,构造函数f(x)=ex+lnx,可知f(x)单调递增,所以应该f(x1)<f(x2),故B 错误;
小结同构式的构建,一般遵循以下几个原则:相同变量放一边;运算形式变相同;有指数有对数都统一为e为底的对数.
三、构造函数解决距离最值
平面中的距离,最值问题除了可用的几何法求解外,也可把其看成函数关系,通过构造函数解析式,化归为某一变量为主参的函数进行求解.
例3(2012年高考新课标卷)设点P在曲线y=上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )
A.1-ln 2 B.
解析由题意知函数y=与函数y=ln(2x) 互为反函数,图象关于y=x对称,函数y=上的点到直线y=x的距离为d=构造函数g(x)=-x(x>0),则g′(x)=-1,知函数g(x)在(0,ln 2)单调递减,在[ln 2,+∞)单调递增,所以当x=ln 2时,函数g(x)min=1-ln 2,即dmin=再由图象关于y=x对称得|PQ|最小值为2dmin=故选B.
小结用于构造一些特殊函数的常见几何意义:
(3)Ax+By表示直线Ax+By+C=0 的截距;
(4)P(cosθ,sinθ)表示单位圆x2+y2=1 上的任意一点;
(5)a2-ab+b2与余弦定理有关.
四、构造函数处理双极值点问题
函数的极值点,即该导函数的零点.而双极值点,即该导函数的两个零点,若导函数为二次函数,则伴随着特殊的韦达定理.所以双极值点问题,常借助韦达定理,减元引参,通过构造函数,可研究该函数的性质解决大小问题.
例4[1](2018年高考新课标Ⅰ卷) 已知函数f(x)=
(1)讨论f(x)的单调性;
(2)若f(x) 存在两个极值点x1,x2,证 明:<a-2.
解析(1) 易知:当a≤0 时,f(x) 在(0,+∞) 上是减函数;当0<a≤2 时,f(x) 在(0,+∞) 上是减函数;当a>2 时,在和上是减函数,在上是增函数.
(2)方法一:由(1)知a>2,0<x1<1<x2,x1x2=1,而

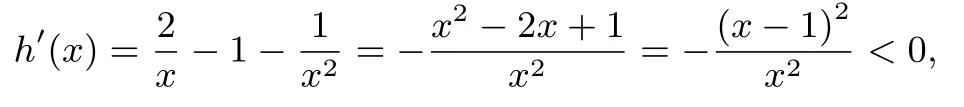
因此h(x) 在(0,1) 上单调递减,所以h(x)>h(1),即2 lnx-x+>0,故2 lnx>x-即原不等式成立.

只需证

即证2alnx2-ax2+<0,(x2>1) 即可,构造函数h(x)=2alnx-ax+(x>1),h′(x)=≤0,因此h(x) 在(1,+∞) 上单调递减,则有h(x)<h(1)=0,所以2alnx-ax+<0 成立,故2alnx2-ax2+<0(x2>1)成立,即原不等式<a-2 成立.
小结构造函数解决双极值点问题,主参的选择有以下途径:
(1)转化为x1或x2的一元函数;
(2)转化为第三变量的一元函数;
(4)两边分别变形为x1,x2的相同结构式,进而构造函数.
五、构造函数处理极值点偏移问题
对于可导函数y=f(x),在区间(a,b) 上只有一个极大(小) 值点x0,方程f(x)=0 的解分别为x1,x2,且a<x1<x2<b,若f(x1)<f(2x0-x2) 时,有<(>)x0,即函数y=f(x) 在区间(x1,x2) 上极(小) 大值点x0右(左) 偏;若f(x1)>f(2x0-x2) 时,有>(<)x0,即函数y=f(x) 在区间(x1,x2) 上极(小)大值点x0右(左)偏.根据上述定义,极值点偏移问题,把自变量的大小问题转化为函数值的大小,再把函数值的大小化归为研究函数的单调性.
例5[2](2010年高考天津卷理科节选) 已知函数f(x)=xe-x(x∈R).
(1)求函数f(x)的单调区间和极值;
(2)若存在实数x1,x2(x1<x2),使得f(x1)=f(x2)成立,证明:x1+x2>2.
解析(1)容易知f(x)在(-∞,1)单调递增,在(1,+∞)上单调递减,f(x)极大=f(1)=
(2)方法一:f′(x)=(1-x)e-x,易得f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,x→-∞时,f(x)→-∞;f(0)=0;x→+∞时,f(x)→0.函数f(x)在x=1处取得极大值f(1),且f(1)=如图2所示.

图2
由f(x1)=f(x2),x1≠x2,不妨设x1<x2,则有0<x1<1<x2,构造函数g(x)=f(1+x)-f(1-x),x ∈(0,1],则

因此g(x)在x∈(0,1]上单调递增,g(x)>g(0)=0,也即f(1+x)>f(1-x)对x∈(0,1]恒成立.
由0<x1<1<x2,则1-x1∈(0,1],所以f(1+(1-x1))=f(2-x1)>f(1-(1-x1))=f(x1)=f(x2),即f(2-x1)>f(x2),又因为2-x1,x2∈(1,+∞),且f(x)在(1,+∞)上单调递减,所以2-x1<x2,即原不等式x1+x2>2 成立.
(2)方法二:由f(x1)=f(x2),得x1e-x1=x2e-x2,化简得两边同时取以e为底的对数,得x2-x1==lnx2-lnx1,即=1,从而

令t=所以要证明x1+x2>2,只需证明lnt>2,构造函数

则有

再构造函数φ(t)=t2-1-2tlnt,(t>1),则

由于t-1>lnt对∀t ∈(1,+∞)恒成立,故φ′(t)>0,φ(t)在t ∈(1,+∞) 上单调递增,所以φ(t)>φ(1)=0,从而M′(t)>0,故M(t)在t ∈(1,+∞)上单调递增,由洛比达法则知

即有M(t)>2,所以lnt>2 成立,即原不等式x1+x2>2 成立.
小结处理极值点偏移问题,函数的构造有以下途径:
(1)构造极值对称差函数f(x0+x)-f(x0-x) 或f(x)-f(2x0-x)(x0为f(x)的极值点);
(2)构造x1或x2一元函数,转化为新函数的最值;
综上,可以体会函数作为主线贯穿高中阶段数学课程的强大功能和重要地位.教学应充分理解函数的内在逻辑和思想方法,掌握应用函数作为工具解题的常见途径,进而培养学生用数学解决实际问题的素养.
——以指数、对数函数同构问题为例

