基于PD控制的四旋翼无人机着陆控制研究

宋志强 方 武 刘孝赵

1(江苏省智能服务工程技术研究开发中心 江苏 苏州 215009)2(苏州经贸职业技术学院信息技术学院 江苏 苏州 215009)3(苏州经贸职业技术学院机电技术学院 江苏 苏州 215009)

0 引 言

近年来，无人机(UAV)越来越多地应用于环保、电力、交通、测绘、安防、农业等民用领域。随着现代技术的进步，特别是人工智能技术的快速发展，未来无人机+行业应用的模式具有广阔的应用前景。目前无人机的智能化水平还有待提高，许多应用背后都有无人机操作员在控制无人机，要提高无人机的自动化和智能化水平，还需科研工作者进行大量研究。无人机的自主着陆问题是无人机智能化应用必须解决的关键技术问题，相比无人机航路规划、导航等方面，自主着陆的研究还相对较少。

张建宏等[1]针对固定翼无人机，采用在线稳定逆研究无人机自主精确着陆问题。高杨军等[2]提出一种内外环混合迭代的滑模控制策略，双环都采用混合迭代滑模控制算法以克服滑模控制的缺点。豆清波等[3]针对小型伞降无人机回收的特点，设计该类无人机全机着陆试验系统并进行着陆试验。许陈元等[4]针对固定翼无人机在着陆过程中速度和下沉率不断增大的问题，采用鲁棒伺服和PID相结合的控制方法设计着陆控制律并进行仿真实验。高九州等[5]针对轮式无人机，根据自适应内模控制原理，以地速与下沉率为控制目标，设计着陆纵向飞行控制律。吴政隆等[6]在分析固定翼无人机着陆阶段运行特性基础上，设计基于光流的自主着陆控制律，并用Simulink进行仿真。以上控制算法通常要依赖GPS导航或惯导系统。由于GPS的缺点，基于视觉的自主着陆吸引了大批研究人员[7]，张小正等[8]基于视觉导航方法，设计圆环型地标并基于此地标研究无人机着陆位姿估计方法。

综上，在固定翼无人机的着陆算法设计方面已有较多研究，但对于多旋翼无人机自主着陆的研究还相对较少。多旋翼无人机在起飞和着陆时不需要跑道，且其可悬停的特性对于监测领域具有非常强的吸引力，因此，研究多旋翼无人机的自主着陆控制具有现实意义。对于强耦合性和非线性系统，线性PD控制是较为简单且行之有效的控制方法，其在工业机器人中已得到广泛应用，本文将PD控制应用于四旋翼无人机的着陆控制，具有工程实践意义。

1 四旋翼无人机动力学模型

四旋翼无人机是MIMO系统，其动力学模型[9]可表示为：

(1)

式中：(x,y,z)为UAV质心在惯性坐标系中的位置，后续仿真中假设UAV可通过自身携带的GPS获得位置信息；θ、ψ、φ为无人机三个姿态的欧拉角，分别为俯仰角、偏航角和滚转角；g为重力加速度；l为无人机半径长度；m为UAV之负载总质量；Ii为围绕每个轴的转动惯量；Ki为阻力系数。UAV着陆控制目标为：x→xd，y→yd，z→0,φ→0。

系统方框图如图1所示。外环产生指令信号θd和ψd，并将其传递至内环系统，采用双环控制方法设计内外环的控制律。

图1 控制系统方框图

2 位置控制律设计

通过设计位置控制律u1以实现x→xd，y→yd，zd→0，其定义如下：

(2)

对于第一个位置子系统，采用基于前馈补偿的PD控制算法设计控制律:

(3)

对于第二个位置子系统，同理设计PD控制律:

(4)

式中：kp2=4.0，kd2=4.0。

对于第三个位置子系统，设计基于前馈和重力补偿的PD控制律:

(5)

假定满足控制律式(3)-式(5)所需要的姿态角度为θd和ψd，为实现θ和ψ对θd和ψd的跟踪，需要求解θd和ψd。由式(2)可得:

(6)

(7)

若X>1，则取θd=π/2；若X<-1，则取θd=-π/2。

3 姿态控制律设计

针对式(1)中的姿态子系统，设计PD控制律，使θ→θd，ψ→ψd，φ→φd。

取θe=θ-θd，采用前馈补偿的PD控制算法设计如下控制律：

(8)

同理，设计第二个姿态控制律为：

(9)

式中：ψe=ψ-ψd，取kp5=16，kd5=16。

设计第三个姿态控制律为：

(10)

4 仿 真

在MATLAB R2017a环境下进行仿真，对于模型式(1)，各参数取值如表1所示。

表1 被控对象仿真参数

被控对象的初始状态取[3 0 2 0 10 0]，角度初始状态取[0 0 0 0 π/6 0 ]。采用位置控制律式(3)-式(5)，姿态控制律式(8)-式(10)，取xd=10，yd=8，zd=0,φd=0，系统在没有干扰的理想状态下，四旋翼无人机着陆时三个位置的收敛过程如图2所示。

图2 x、y、z三个位置状态收敛曲线

系统在没有干扰的理想状态下，四旋翼无人机着陆时三个姿态的收敛过程如图3所示。

图3 三个姿态收敛曲线

从收敛曲线可看出，四旋翼无人机着陆于(10,8,0)，着陆过程平稳，收敛速度较快，三个位置收敛于期望值，没有出现超调现象。采用内环收敛速度大于外环收敛速度的方法，可保证闭环系统稳定性。

仿真时，若系统中存在有限带宽白噪声，则四旋翼无人机着陆时三个位置的收敛过程如图4所示。

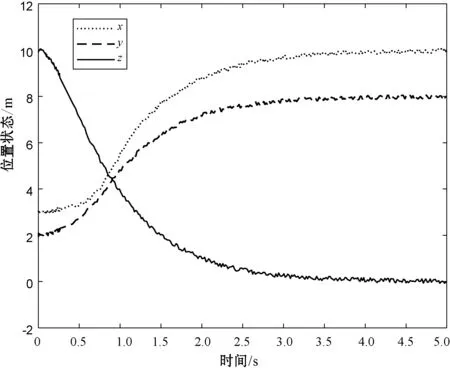
图4 系统存在白噪声时x、y、z三个位置状态收敛曲线

从收敛曲线可看出，引入白噪声后，系统位置状态曲线总体收敛，存在超调但幅度较小，最终四旋翼无人机着陆于(10,8,0)附近。从仿真结果可看出，在系统存在扰动的情况下，双环PD控制算法也具有实用性。

5 结 语

无人机的自主着陆问题是无人机智能化应用必须解决的关键技术问题。四旋翼无人机是行业应用中最为典型的机种，其动力学模型具有多输入多输出、强耦合的特点，针对其模型，设计基于双环的PD控制的着陆算法，外环控制位置，内环控制姿态。将外环产生的中间指令信号θd和ψd传递给内环，内环通过内环控制律实现对两个指令信号的跟踪，通过调整内外环增益系数保证闭环系统的稳定性。PD控制器在工程上容易实现，可用于实时性较高的场合。