基于二阶牛顿插值的图像自适应缩放设计及实现

王 康 杨瑞祺 杨依忠 解光军

(合肥工业大学电子科学与应用物理学院 安徽 合肥 230601)

0 引 言

图像缩放技术被广泛地应用于各类消费类电子产品、医学图像处理以及安防监控等领域中[1-3]。图像缩放处理算法的种类较多，根据算法是否对边缘进行处理，可以大致分为线性的图像插值算法和非线性的图像插值算法[4]。线性的插值方法如最邻近插值、双线性插值和双三次插值等经典的插值算法[5-6]，在计算目标图像的像素时只通过其位置和邻域内的原始像素数据计算，不考虑边缘处的图像信息变化，缩放后效果会导致边缘模糊不清。葛晨阳等[7]设计了一种图像混合插值缩放的IP核，其相较于双三次插值硬件消耗少，但也没有对图像边缘进行处理。对于非线性的插值算法，研究较多的是基于边缘的图像缩放算法。边缘检测算法包括Sobel[8]、Prewitt[9]和Canny[10]以及基于形态学的边缘检测算法[11]等。Chen等[12]提出的基于Sobel算子的边缘插值算法和尉成勇等[13]提出的改进边缘方向判定的图像插值算法分别通过Soble算子和Canny算子对图像边缘进行检测，然后对边缘进行一维的方向插值计算，非边缘采用线性插值的方法，这样会使边缘区域的非边缘像素参与边缘区域计算，导致得到的目标图像仍会有一些模糊。还有一些采用边缘自适应缩放的算法，如Cha等[14]提出了一种误差修正的边缘插值方法(EASE)，但算法复杂度较高。王效灵等[15]和李自勤等[16]提出边缘自适应图像缩放算法(EASA)，采用平均思想找到边缘位置，然后选取边缘方向上的点进行插值计算，该算法需要考虑插值点邻域内多个像素点，且不同方向的插值系数计算复杂。李春龙等[17]提出自适应立方卷积算法，在平缓区域采用双三次插值算法，在边缘区域根据插值点的位置进行两轮插值，虽然效果不错，但运算量大。齐敏等[18]通过数据融合的方式对不同区域的插值点进行插值计算，算法通过多次归一化方法求系数，但缩放效果并不理想，且计算过程繁杂。刘政林等[19]提出基于边缘的实时缩放算法，在边缘检测上考虑欠缺，导致边缘区域的缩放效果不佳。叶森等[20]提出一种基于三次拉格朗日的插值算法，但该算法只考虑了水平方向和竖直方向的边缘检测，忽略了45度和135度方向上的边缘检测，且计算复杂。此外，詹毅等[21]提出一个变指数变分模型的插值算法，范清兰等[22]提出一种基于NSCT的区域自适应图像插值算法，Lee等[23]提出一种利用泰勒级数近似的边缘引导图像插值方法，以及近些年提出的基于深度学习的图像插值算法[24]等。尽管这些算法的缩放效果不错，但都比较复杂，难以用硬件实现。

基于上述分析，本文提出一种基于二阶牛顿插值的自适应缩放算法。对处于非边缘位置的像素点，根据插值点位置关系选择一组合适的计算方法得到目标像素值。对处于边缘位置的像素点，不是简单采用对边缘进行一维插值的方法，而是对多个方向及其相关度进行权重分配计算得到目标像素值。处理结果相比传统的缩放算法效果更好，且计算复杂度低，利于硬件实现。

1 算法设计

在对图像进行实时缩放处理时，通常对二维图像的水平方向和垂直方向分别进行插值处理。假设把分辨率为M×N原始图像缩放为分辨率为U×V的目标图像，可以先对水平方向进行缩放得到大小为U×N的中间图像，然后再对该中间图像垂直方向进行缩放得到目标图像。对水平方向进行缩放只需考虑一维方向的缩放处理，假设对水平方向进行插值处理，将一行像素序列看成距离为1的等距节点，则目标像素点与原始图像在水平方向上的位置关系如图1所示。其中：f是目标像素点在水平方向上映射到原始图像中的位置；f1、f2、f3和f4为f水平邻域内的四个原始像素点；Δx是f和f2之间的距离，取值范围为0≤Δx<1，且t=1+Δx。

图1 目标像素水平方向插值示意图

选取二阶牛顿插值算法来计算f的像素值时，可以用f1、f2和f3三个原始像素点作为一组像素或f2、f3和f4三个原始像素点作为一组来计算目标像素f的像素值，两种方式的插值公式分别为：

(1)

(2)

式中：Δf1和Δf2分别为f1和f2的一阶差分；Δ2f1和Δ2f2分别为f1和f2的二阶差分。

当f处于非边缘位置时，所有计算结果几乎一致，如果插值位置位于边缘区域时，考虑到其位置以及相关性，需要选取其中的一组来计算以得到更逼近边缘位置像素点的像素值。将t=1+Δx代入式(1)和式(2)进行化简可得：

(3)

(-Δx2+2Δx)f3

(4)

由插值理论可知，当f点处于边缘位置时，如果接近f2，则希望计算目标像素的像素值更接近f2的像素值，如果接近f3，则希望计算目标像素的像素值更接近f3的像素值，这样可以使插值图像的边缘宽度变窄，不会因边缘宽而导致插值图像的边缘模糊。从式(3)和式(4)可以看出，选取第一组像素时f1所占权重和选取第二组像素时f4所占权重一样，两像素点对计算目标像素的影响也一样。下面分别考虑两组计算公式中f2和f3的权重对目标像素的影响。

对式(3)中f2的系数和式(4)中f2的系数设定关于Δx的函数为y1和h1，如图2所示。对式(3)中f3的系数和式(4)中f3的系数设定关于Δx的函数为y2和h2，如图3所示。

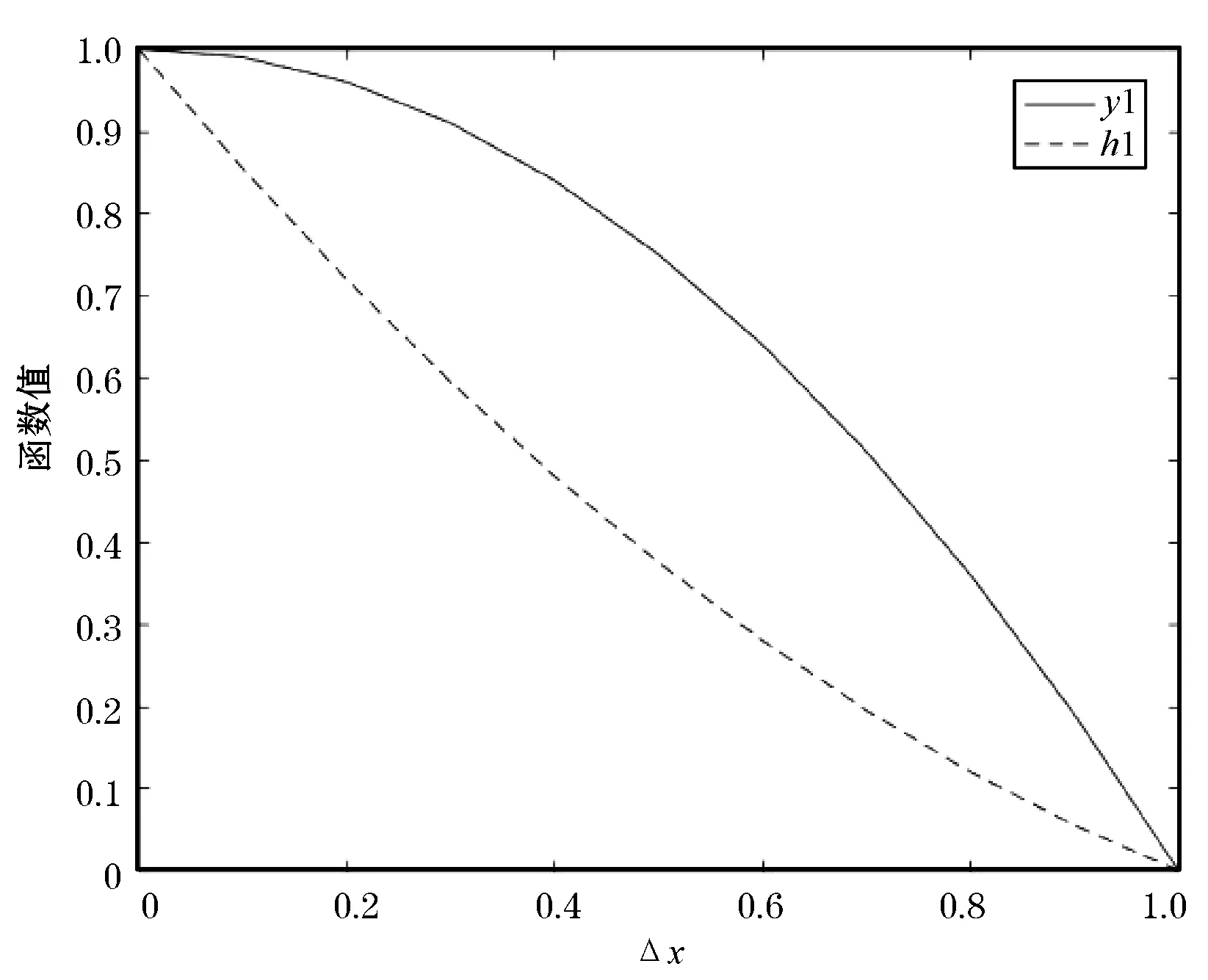
图2 第一组f2权重函数和第二组f2权重函数

图3 第一组f3权重函数和第二组f3权重函数

当Δx小于0.5时，从图2中可以看到y1的值一直大于h1的值，经求导得到y1的导数始终小于h1的导数，并且当Δx越小时，y1的导数越小，h1的导数越大。这说明当插值点f接近f2点时，第一组公式f2所占权重大于第二组，且第一组f2的权重随着Δx增大缓慢减小。从图3中可以看出，h2的值此时一直大于y2的值，说明当插值点f接近f2时，第一组公式f3所占权重小于第二组，且通过h2和y2的导数可知第一组f3权重随着Δx增加缓慢变大。由此，当Δx小于0.5时，选取第一组公式计算得到的目标值更接近f2的像素值。同理，当Δx大于0.5时，选取第二组公式计算得到的目标值更接近f3的像素值。因此，对于水平方向缩放的插值计算公式可改写如下：

(5)

由水平缩放过后得到中间图像，需再对中间图像45度、135度和垂直方向进行缩放处理以得到目标图像。其插值示意图如图4所示。

图4 中间图像插值示意图

图4中空心圆形和空心菱形分别表示插值点距离像素点f(i,j)小于0.5和大于0.5两种情况，实心圆点分别是插值点邻域内的各原始像素点。对水平缩放后的中间图像进行垂直方向上的缩放，假设空心圆为目标像素点所在位置，u的值小于等于0.5，根据水平方向的插值原理，在f(i,j)的3×3邻域内分别选取垂直方向、45度方向和135度方向各一组像素，计算其二阶差分分别为Δ2f1、Δ2f2和Δ2f3。将阈值T分别与Δ2f1、Δ2f2和Δ2f3的绝对值进行比较，如果三者中有小于T值的，则说明在该方向上是像素值变化较小的平缓区域。依次按照垂直方向、45度方向和135度方向进行判断是否小于T，直到首次符合条件时，就利用该方向上三个像素点进行二阶牛顿插值计算得到目标像素值。对于三者都大于T时，则说明该目标像素在三个方向都不处于平缓区域，需利用三个方向的像素点进行计算得到目标像素值。方法如下：

考虑到二阶差分越小的方向，其相关性越大，所占权重应该越高，对Δ2f1、Δ2f2和Δ2f3进行归一化处理，得到三个方向的权重系数，公式如下：

(6)

(7)

(8)

同时，根据式(5)计算三个方向的二阶牛顿插值结果，为简化计算，对于45度和135度方向上Δx的值直接选用垂直方向上Δx的值，即图4中u的值，计算得到三个方向的结果分别为F1、F2和F3，与各自方向上的权重系数相乘后再求和，因为三个方向权重系数之和为2，所以最后需乘以1/2得到目标像素值，计算公式如下：

(9)

同理，假设目标像素位置处于图4中空心菱形的位置，即u大于0.5，则选择f(i,j+1)像素点3×3邻域的像素点，采用同样的方法计算目标像素点的像素值。

考虑到边缘位置的判断，通过设定一个阈值T作为参数。参数选取的大小会导致缩放效果不同，通过实验，选取不同的参数T对多组不同图像进行先放大两倍再缩小到原图像大小，然后求出不同阈值下缩放过后的峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和边缘保护指数(Edge Protection Index, EPI)。通过对比实际缩放后视觉效果，以及对PSNR和EPI比较分析，本文算法选取阈值T为50。

2 实验结果分析

实验选取了2幅大小为256×256像素的灰度图像House和Baboom，3幅大小为512×512像素的灰度图像Items、Ruler和Bicycle作为原始图像。使用双线性插值算法[5]、双三次插值算法[6]、数据融合算法[18]、边缘插值算法[19]及本文算法对图像进行缩放处理。

2.1 缩放结果图对比

为了直观地对比不同算法处理的效果，以灰度图像Ruler的实验结果为例。截取图像处于边缘且大小为60×60像素的区域图像，将原图中60×60像素大小的原图截取放大，如图5(c)所示，放大后可以清楚地看到原图像中区域的细节，使得对比效果更加直观，再分别用双线性插值算法、双三次插值算法、数据融合算法、边缘插值算法和本文算法对其放大后得到大小160×160像素的图像。

图5 Ruler放大后不同算法结果

由图5可知，双线插值算法缩放后由于高频分量丢失而导致图片整体变得模糊，双三次插值的效果比双线性插值要好些，但由于两种算法都未考虑到对图像边缘进行处理，因此边缘处理效果都不好。数据融合算法同样由于高频分量丢失，导致放大后图像模糊。边缘插值算法在边缘处仅考虑了水平和垂直方向上像素的相关性，并未考虑45度和135度方向上的相关性，且没有考虑到插值点最近位置像素所占权重问题，因此处理后的结果也不尽如人意，甚至对部分图像处理的结果没有双三次插值的效果好。而本文算法在边缘处和细节丰富区域的处理更接近原图，虽然进行了放大处理，图像的细节和原图接近，说明其高频分量得到保持。同时边缘纹理和原图基本一致，说明其在边缘处理上效果也相对较好。因此，本文算法对图像的缩放总体效果更优。

为了更进一步比对不同算法处理效果，将Bicycle原图中60×60像素大小的原图截取图放大至更大比例的4倍，如图6(c)所示，可以清楚地看到原图像中区域的细节，同时采用不同算法分别对60×60像素大小的截取图4倍放大后显示，结果如图6(d-k)所示。可以看出，双线性插值、双三次插值和数据融合算法放大后边缘区域已经比较模糊，边缘插值算法放大后的图像出现一定程度的失真而本文算法在放大4倍后仍能够保留边缘的信息且抑制了高频分量丢失导致图像模糊的情况。

图6 Bicycle放大4倍后不同算法结果

2.2 客观评价指标对比

峰值信噪比(PSNR)是最常用的客观评价图像处理效果的量化指标，其计算公式如下：

(10)

式中：F0代表大小为M×N像素的原始图像；F表示处理过后的和原图像相同大小的图像。PSNR越大，表示目标图像信息损失越少，图像越接近于原始图像，处理效果则越好。

从客观评价指标的角度说明边缘保护效果的好坏，通常用边缘保护指数(EPI)作为评价指标，其计算公式如下：

(11)

式中：ps表示处理过后的图像；po表示原始图像。EPI值越接近1，则边缘保护得越好。

实验选用了House、Baboom、Items、Ruler和Bicycle图像，用不同算法分别放大两倍再缩小还原，计算其峰值信噪比(PSNR)的值和边缘保护指数(EPI)的值，结果分别如表1和表2所示。从表1中可以看出，本文算法相对于其他4种算法，PSNR均有大幅度的提升。从表2中可以看出，本文算法的EPI与其他4种算法相比更接近1，对边缘的保护最好。可见，本文算法对图像的处理效果明显优于其他4种算法。

表1 不同算法PSNR

表2 不同算法EPI

3 算法硬件实现

3.1 硬件实现方案

硬件实现方案如图7所示，首先通过行数据缓存模块对输入的图像数据进行行缓存，采用FPGA的内部存储资源，用三组line-buffer来实现，因为在水平方向利用二阶牛顿插值需要用到三个像素点来进行计算，为了实现并行运算，采用三组line-buffer同时缓存一行像素数据。然后通过水平方向的插值计算模块完成对水平方向的插值计算，将计算得到的数据结果暂存到异步FIFO中，等待一行像素计算完成以后，再将异步FIFO中的数据送入到外部的DDR3存储器中，其原因是为了满足DDR3的高速要求，FIFO模块采用两组进行乒乓操作。等一帧图像水平插值完成以后，再从DDR3中读取数据。通过列数据缓存单元将用于插值计算的三列数据从DDR3中读出存入line-buffer中，对垂直方向、45度方向和135度方向分别进行插值计算。最终将插值计算的结果存入输出缓存模块中，将数据输出。其中DDR3控制器直接调用IP核来实现DDR3的读写控制。

图7 硬件实现方案

3.2 硬件设计

根据硬件实现方案，下面以最主要的水平插值模块和多方向插值模块为例进行硬件设计说明。

3.2.1水平插值模块设计

首先使用line-buffer对图像的行数据进行缓存，坐标系数生成模块通过对缩放系数进行累加确定源像素地址和插值系数，然后根据像素地址从line-buffer中读取参与计算的三个相邻像素点，最后通过插值计算模块计算出目标像素值，从而完成水平方向的缩放处理。模块设计原理如图8所示。由于设计中缩放系数使用浮点数计算，需对其放大256倍处理，放大后缩放系数用24位二进制数表示，其中后8位为插值系数，用于确定各像素点权重，前16位整数部分用于确定目标像素位置。

图8 水平插值模块硬件设计原理图

3.2.2多方向插值模块设计

多方向插值模块的设计原理和水平插值模块原理类似。先从列数据缓存器中读取目标像素3×3邻域内用于计算的7个像素点，分别计算出垂直方向、45度方向和135度方向的二阶差分和二阶牛顿插值结果，将结果存入寄存器中。之后将二阶差分与设定的阈值比较作为后续多路选择器的判断条件，如果判断为非边缘区域，多路选择器会选择一个方向的插值结果作为最终插值结果；如果判断是边缘区域，则通过式(9)计算得到最终的插值结果。模块设计的仿真结果如图9所示，其中信号T为设定阈值，信号k为垂直方向插值系数，从列数据缓存模块读取的是相邻三列数据，在沿水平方向计算完成后，k的值才会更新。输入的7个像素点信号分别是f_00、f_01、f_02、f_11、f_20、f_21和f_22，三个方向的二阶差分绝对值对应的信号分别为r_h11、r_h22和r_h33；信号F1、F2和F3分别是用24位的二进制数表示的三个方向的牛顿二阶插值结果；信号o_pixel为最终输出的目标像素值。由于采用流水线的设计方法，最终输出的目标像素比输入像素延迟了两拍。

图9 多方向插值模块仿真结果图

3.3 FPGA实现及验证

硬件实现和验证所使用的FPGA开发板选用的是ALTERA公司Stratix V系列的5SGXEA7N2F45C2N FPGA开发板。在Quartus II 15.0软件平台上完成了设计及验证。FPGA设计验证平台如图10所示，首先通过Quantum Data980给出视频图像的RGB数据、水平同步信号、垂直同步信号和使能信号到FPGA，再将FPGA对数据进行缩放处理，再将TTL转HDMI桥接芯片将信号转换成HDMI标准的信号格式，最后输出到显示器上。FPGA实现及验证装置如图11所示。

图10 FPGA设计验证平台

图11 FPGA实现及验证装置

实验选取了2幅512×512像素大小的图像进行验证，将其放大到1 024×1 024像素大小后输出到显示器上，得到的结果如图12所示，可以看到输出结果效果良好。

图12 硬件验证结果

4 结 语

本文提出一种基于牛顿二阶插值的边缘自适应缩放算法，对原始图像的水平方向根据插值点映射的位置利用二阶牛顿插值算法进行插值计算得到中间图像，着重考虑垂直方向、45度方向和135度方向上的相关性，通过计算三个方向上的二阶差分并与阈值作比较，选择合适的算法计算得到目标像素值。对算法进行硬件的实现与验证，结果表明，无论从图像处理效果还是客观评价指标结果看，本文算法与其他相关算法相比，其缩放效果及对图像边缘的保护明显有优势，且算法复杂度不高，利于硬件实现。