六自由度平台角位置测量精度方法
李永强,卢明涛,马建明,邓慰敬
(北京航天控制仪器研究所,北京100039)
0 引言
随着机器人技术不断地发展,因其较高的刚度、稳定性以及可同时提供多自由度的运动特性,六自由度平台在众多高科技行业的模拟仿真中发挥着重要作用[1-2]。现已研发出来的六自由度平台大多应用在无人机运动仿真、车载运动仿真、船舶运动仿真、导弹运动仿真、航空航天设备等的半实物仿真中[3-4]。
应用六自由度平台进行半实物仿真过程中,平台运动的精度将直接影响半实物仿真结果的真实性。因此,六自由度平台各自由度运动精度的保证对仿真结果尤为重要。目前,国内外在六自由度平台参数指标测试时,线位置精度大多采用激光干涉仪和激光跟踪仪进行测量,而角位置精度几乎均采用激光跟踪仪进行测量[5-7]。激光跟踪仪的使用和维护成本较高,原理及操作较为复杂,且国内拥有激光跟踪仪的单位和机构非常少。因此,寻求一种测量相对简单、测量及维护成本较低的测量方法具有很高的应用价值。
针对该问题,本文提出了一种测量成本低、测试方法及操作较为简单的六自由度平台角位置精度测量方法。在测量角位置精度时,该方法应用倾角仪、光电自准直仪以及带棱镜的360多齿分度盘等仪器对横滚、俯仰以及偏航三个方向的角位置精度及重复性精度进行测量,方法简单,能够快速准确地测出各自由度角位置精度等参数,且成本较低。
1 六自由度平台结构及控制系统
1.1 六自由度平台整体机械结构
本文对某Stewart六自由度平台进行角位置精度及重复性测量,验证所设计测量方法的可靠性。六自由度平台的结构示意图如图1所示,其为并联结构,各轴均采用电动缸驱动。上铰及下铰处所用轴承均为FAG角接触轴承,各轴电动缸均采用美国EXLAR原装K系列伺服缸,各轴驱动电机均采用菲仕电机且配备EQN1325编码器。该六自由度平台上铰圆半径Ra=0.4m,下铰圆半径Rb=0.54m,平台处于工作零位时电动缸上下铰点间的距离L2=0.72m,上铰相邻铰之间的短边距离da=0.1m,下铰相邻铰之间的短边距离db=0.2m,电机与缸的安装方式为平行安装方式。如图1所示坐标系,绕X轴转动的为横滚运动,绕Y轴转动的为俯仰运动,绕Z轴转动的为偏航运动,O为平台中心点(平台运动的中心)。
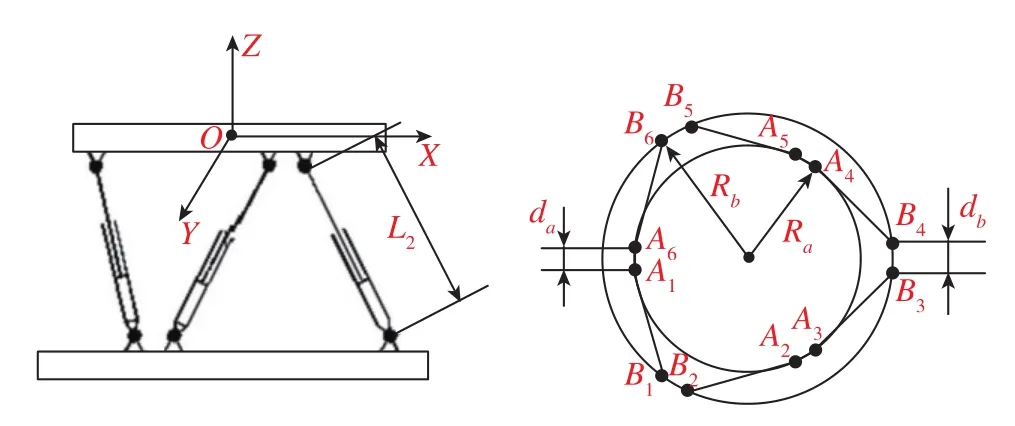
图1 六自由度平台结构示意图Fig.1 Structure diagram of 6-DOF platform
1.2 六自由度平台控制系统
六自由度平台控制系统由上位机与下位机组成,其示意图如图2所示。上位机采用半加固型笔记本电脑,运行系统为Windows系统;下位机采用ACP-4000工控机,其运行系统为RT实时系统;上位机、下位机均采用LabVIEW软件进行编程控制。整个控制系统的硬件中,电机的驱动控制单元均采用美国Copley公司XPL系列驱动器进行控制。驱动器与下位机之间为CAN通讯形式,使用的是NI公司的CAN卡,上位机与下位机之间采用网口通讯形式。整个控制系统采用三相220VAC/50Hz进行供电,控制系统能够稳定的运行,上位机、下位机能够实现实时通讯,满足六自由度平台的控制要求。
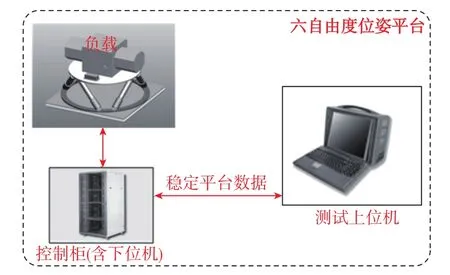
图2 六自由度平台控制系统示意图Fig.2 Diagram of 6-DOF platform control system
2 角位置参数检测方案设计
2.1 倾角仪测试原理
角度测量在几何量计量技术中占据重要位置,倾角仪被广泛应用在角度测量中[8]。当倾角仪处于静止状态时,由于其只受重力作用,其重力垂直轴与传感器灵敏轴间的夹角即为所求倾角[9-10]。图3为倾角仪工作原理示意图。在安装倾角仪之前,应使用电子水平仪将六自由度平台中位水平调整在30″以内,同时在与中位同一水平面的基准面上安装倾角仪,保证倾角仪X轴方向与Y轴方向的敏感轴与六自由度中位的X轴方向与Y轴方向一致。通过水平精度的调整以及基准面加工精度的保证,倾角仪与六自由度平台固联后,平台运动过程中可以忽略重力分量等对倾角仪测量精度的影响。当倾角仪相对敏感轴X方向或Y方向发生一个转动角度时,倾角仪会将该角度测量出来,从而得出横滚运动或俯仰运动的运动角度。
图3 倾角仪工作原理示意图Fig.3 Working principle diagram of inclinometer
本文测量时使用的倾角仪为Jewell公司制造的DXI-100系列的数字倾角仪,其实物图如图4所示。该倾角仪内部为集成形式,测量精度达到0.005°、分辨率达到0.001°的数字输出,具有噪音低、稳定性高、工作温度范围大等性能。测试过程中,上位机与倾角仪通过RS485串口进行通信。六自由度平台运动平稳后,倾角仪能够得到平台在X轴方向或Y轴方向的运动角度并显示在上位机界面上,从而确定横滚及俯仰两个方向的角位置测量精度。

图4 倾角仪实物图Fig.4 Physical drawing of inclinometer
2.2 光电自准直仪测试原理
光电自准直仪是依据光学自准直成像原理,通过LED发光元件和线阵CCD成像技术设计而成。它由内置的高速数据处理系统对CCD信号进行实时采集处理,同时完成角度测量[11],其测试原理图如图5所示。

图5 光电自准直仪测试原理图Fig.5 Test schematic diagram of photoelectric autocollimator
在光源处发射出一束光,光经过狭缝、分束器、准直物镜后射到反射镜上,通过反射镜将光反射回去,形成的图像由光感接收器接收。光电自准直仪的光轴在照射到棱镜相邻镜面的不同位置时会引起一个微小的偏差,光电转换系统敏感光学信号并将其转换为电信号供后续处理,该偏差经过光电自准直仪的CCD线阵能够被精确的测出[12-13]。反射镜在位置1和位置2时,CCD线阵上的狭缝图像位置如图6所示。其中,Δy为反射镜在位置1时CCD线阵上的狭缝图像位置与反射镜在位置2时CCD线阵上的狭缝图像位置的偏差。

图6 CCD线阵示意图Fig.6 Schematic diagram of CCD linear array
测量出的偏转角α即为误差,该误差为六自由度平台偏航运动时角位置精度的测量值,α可通过以下公式计算得到

式(1)中,f为准直物镜的焦距。
本文在测量角位置精度时使用的光电自准直仪是德国的ELCOMAT 3000系列,其实物图如图7所示。该光电自准直仪的分辨率最高能够达到0.005″,精度可达0.1″且性能较稳定。

图7 光电自准直仪实物图Fig.7 Physical drawing of photoelectric autocollimator
2.3 360多齿分度盘测试原理
360多齿分度盘配合多面棱体能够提供1°~360°的角度测量,图8为安装有棱体的360多齿分度盘。在测量角位置时,齿盘随着平台运动到指定位置后,将手柄松开,反向转动齿盘使齿盘转动刚刚平台运动的角度,然后合上手柄固定齿盘,再使用光电自准直仪进行角位置精度测量。由于齿盘的加工精度极高,实验过程中使用的齿盘精度能够达到1″,可满足整体测试要求。

图8 360多齿分度盘实物图Fig.8 Physical drawing of 360 multi-tooth index plate
2.4 总体检测方法
(1)角运动幅值检测方法
利用数字式电子水平仪将六自由度平台水平调整在误差允许范围内后,在倾角仪安装基准面上将倾角仪安装,使其敏感轴与X轴及Y轴重合,并将倾角仪通电与上位机进行通信。打开倾角仪通信软件,在六自由度平台零位位置通过倾角仪通信软件将读数置零。将该位置默认为零位,将六自由度平台横滚和俯仰两个方向的角位置分别设定为要求的最大限位值。启动平台,平台达到相应极限位置后,读取并记录平台在这两个运动方向的最大运动范围。
沿Z轴方向(偏航运动)安装带有棱镜的360多齿分度盘,并架设光电自准直仪,同样将六自由度平台沿Z轴方向转动的位置设定为要求的最大限位值。启动平台,平台达到相应的极限位置后,手动转动多齿分度盘,反向转动平台所运行的角度并保证光电自准直仪有读数,运动的最大极限范围即为该运动方向运动范围。
(2)角位置定位精度测量方法
首先,测量横滚及俯仰两个方向的角位置测量精度。在基准面上安装好倾角仪后,将倾角仪读数设置为零位。从平台系统横滚或俯仰极限位置-10°开始,记录倾角仪读数α1。以数字显示为准,依次使平台沿着X轴方向正向间隔2°运动直至运动到+10°位置,记录倾角仪的其它相应读数α2、α3、 …、αi, 目标位置分别记为α01、α02、…、α0i,i=N(N为测量点数)。 再分别依次间隔2°将平台反向运动一趟,记录下正反运动的2组数据。
以上两个方向测量完成后,对偏航方向的角位置精度进行测量。调整好平台后将六自由度平台运行至零位,将带有棱镜的齿盘安装在六自由度平台运动中心(Z轴方向)。光电自准直仪和被测平台放置在同一隔震地基上,使光电自准直仪的光轴线垂直于带有棱镜的齿盘。从平台系统角位置数字显示-10°开始,记录光电自准直仪读数α1。 以数字显示为准,依次使轴正向间隔2°转动直至转到+10°位置,记录光电自准直仪的其它相应读数α2、α3、 …、αi,i=N(N为测量点数)。 再分别依次间隔2°将平台反向运动一趟,记录下正反运动的2组数据。
根据仪器测得的数据与目标位置的关系,可以得到三个运动方向的角位置定位精度
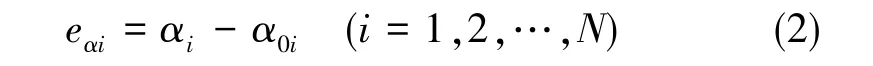
式(2)中,eαi为以角位置测量系统数字显示0为准的圆周分度误差,即实际值与目标值之间的差值,测量偏航运动方向时该值为消除棱体误差后的值。被测运动方式正向运动时,取eαi中最大分度误差为(正值)和最小分度误差为(负值);被测运动方式反向运动时,取eαi中最大分度误差为(正值)和最小分度误差为e2-i(负值)。
通过式(3)可得到被测方向的角位置定位精度,即平台正方向或反方向运动时误差峰峰值的1/2。

式(3)中,εj为第j次测量的角位置定位精度。取正向运动位置精度与反向运动位置精度的最大值作为该平台的角位置精度,其计算方法如下

根据平台正反两次运动测得的数据,对被测方向的角位置重复精度进行计算。
在六自由度平台做角运动时,其横滚、俯仰及偏航运动可以看做是分别绕X轴、Y轴、Z轴的转动,参照GJB-1801惯性技术测试设备主要性能测试方法[14],可通过式(5)计算得到各方向的角位置测量重复性

式(5)中,e1,i=α1,i+1-α1,i(i=1,2, …,N)为被测方向正向运动时相邻测试点实测值之间的差值,e2,i=α2,i+1-α2,i(i=1,2, …,N)为被测方向反向运动时相邻测试点实测值之间的差值,N为正转或反转时测量的点数。
3 六自由度平台角位置精度测试
为验证所设计测试方法的可行性及稳定性,对某Stewart平台进行角位置测量精度的实验,包括横滚、俯仰及偏航三个运动方向的角运动范围、角位置测量精度及角位置测量重复性,并对测试结果进行处理分析。测试现场如图9所示。

图9 测试现场Fig.9 Diagram of test site
实验以六自由度平台为测试对象,控制运动平台按照所设计的测试方法逐点运动。通过倾角仪测量横滚及俯仰两个方向的运动角度,使用带有棱镜的360多齿分度盘及光电自准直仪对偏航方向的运动角度进行测量。三个运动方向均采集22个实验点,即平台正向运动和反向运动各取11个实验点。对记录的数据进行分析处理,可得到其角位置测量精度及角位置测量重复性,测试数据及数据处理结果如表1~表3所示。

表1 六自由度平台横滚方向角位置精度测量结果Table 1 Measurement results of angular position accuracy of 6-DOF platform in roll direction
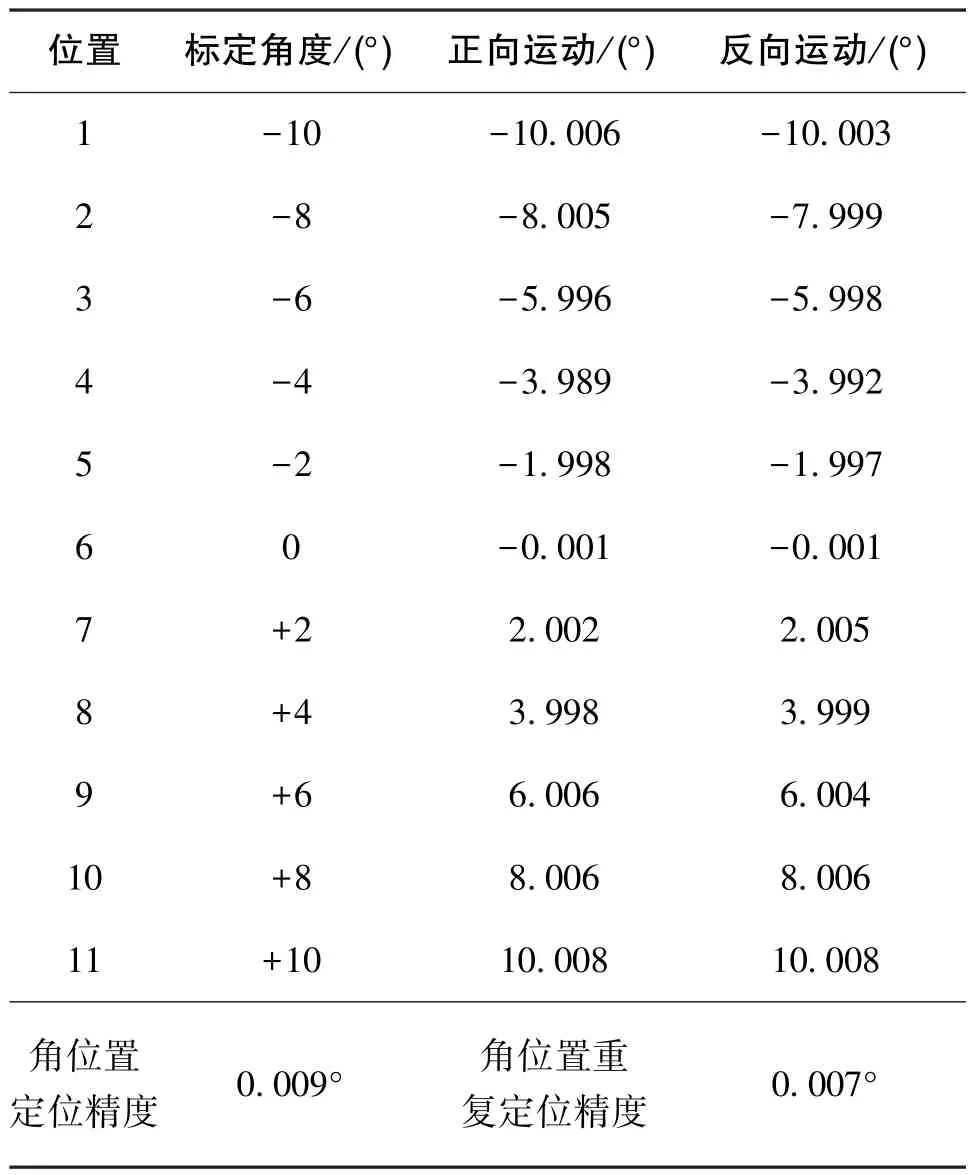
表2 六自由度平台俯仰方向角位置精度测量结果Table 2 Measurement results of angular position accuracy of 6-DOF platform in pitch direction
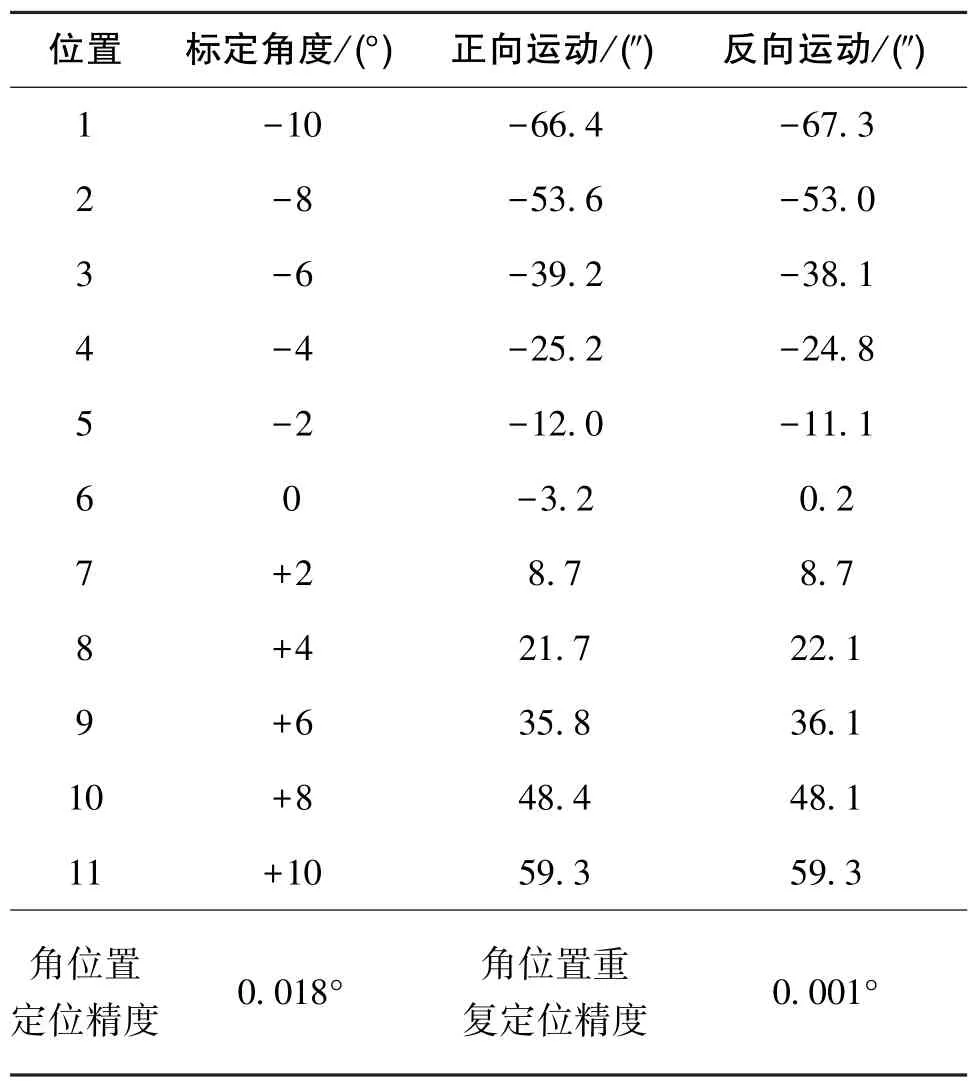
表3 六自由度平台偏航方向角位置精度测量结果Table 3 Measurement results of angular position accuracy of 6-DOF platform in yaw direction
从以上实验测试数据的处理结果可以看出:横滚、俯仰及偏航三种运动形式的角运动范围均为-10°~+10°,角位置测量精度分别达到0.012°、0.009°、 0.018°, 测量重复性分别达到 0.005°、0.007°、 0.001°。
对平台三个运动方向的测量结果进行处理,可以得到如图10所示的各运动方向的正向运动和反向运动的角位置测量误差范围。通过计算,也可得到各运动方向的角位置测量重复性。实验过程中,倾角仪和光电自准直仪能够快速准确地测量出三个方向的角运动位置。
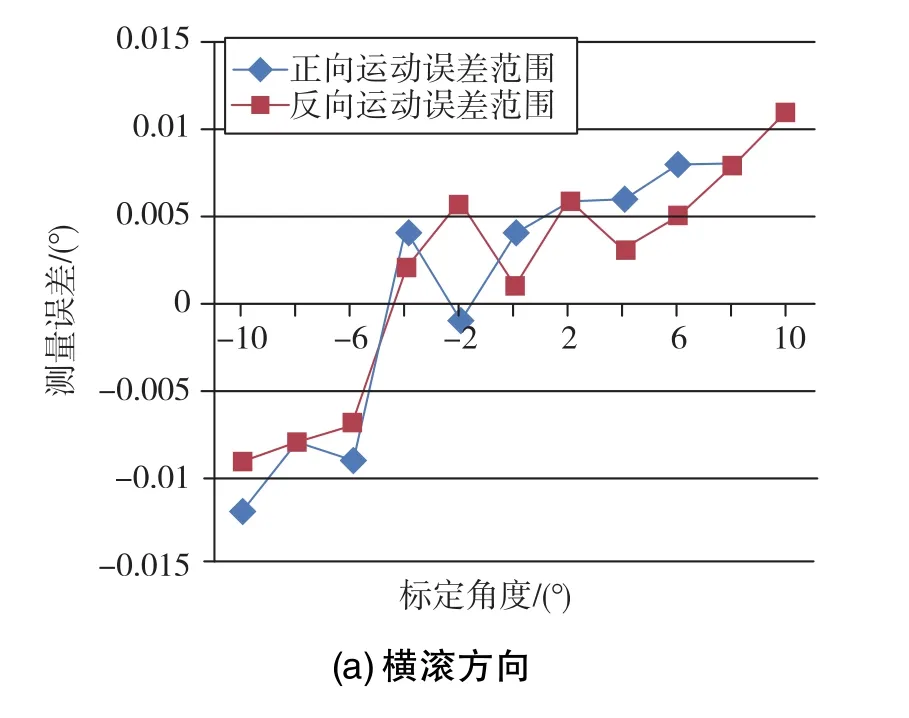
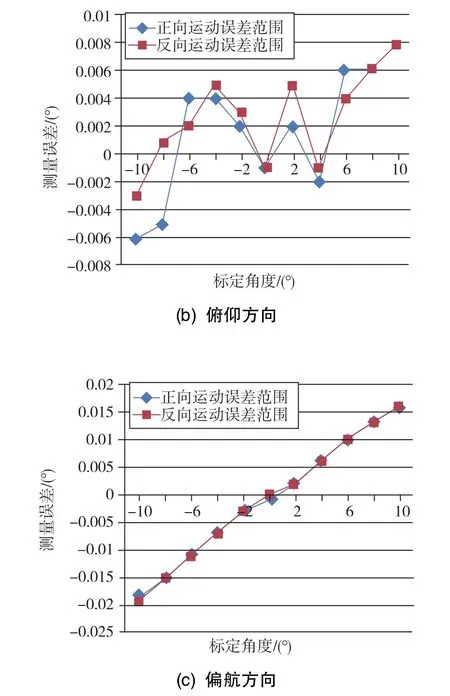
图10 角位置测量误差范围Fig.10 Error range of angular position measurement
Stewart平台进行速度反解时,考虑到平台有六个缸,根据相关资料[15]可以得到上平台广义速度到缸伸长速度的Jacobi矩阵Jlq

式(6)中,Ln为缸轴线方向单位矢量组成的矩阵,Ap为上铰链中心在台体坐标系中的坐标矩阵,R为动坐标系到静坐标系的方向余弦阵。
由式(6)可知,该Jacobi矩阵只与平台的结构尺寸及其位姿有关。当运动学Jacobi矩阵中各元素量纲都一样时,基于运动学Jacobi矩阵的条件数性能指标函数的定义如下[16-17]
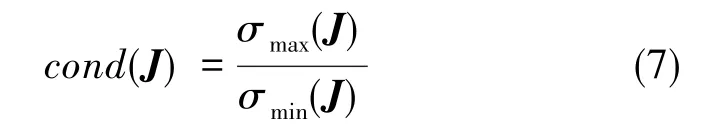
式(7)中,cond(J)为某位姿时基于运动学Jacobi矩阵J的条件数性能指标函数,σmax(J)为某位姿时J的最大奇异值,σmin(J)为某位姿时J的最小奇异值。
由式(7)可知,当Jacobi矩阵Jlq越接近奇异即平台运动越接近临界运动范围时,其条件数越大。条件数是评价机器人性能最常用的性能指标函数,条件数越大,进行反解时会使速度的输入与输出传递过程严重失真,最终导致平台的运动误差增大。从图10各运动方向的角位置测量误差范围可以看出:最大正向运动及最大反向运动的角位置测量误差出现在+10°和-10°位置处,而且三个方向所测量的角位置误差相对各自的运动轴具有一定的线性关系,该结果也验证了Stewart平台在其极限运动范围处Jacobi矩阵的条件数最大,呈现病态。导致平台的运动以及动力传递特性最差的固有特性,即随着平台向极限位置运动的过程中,平台自身产生的运动误差也随之增大,同时也从侧面反映了该测试方法的准确性及可行性。
4 结论
针对目前六自由度平台角位置精度测量方法较少、测量成本较高且测试原理及操作繁琐的实际情况,本文提出了一种六自由度平台角位置精度测量方法。该测量方法原理相对简单、操作方便且使用和维护成本较低,能够快速准确地测量出各运动方向的角位置测量精度、角位置测量重复性以及幅值范围等。本文结合实验室现有某Stewart平台,对其角位置测量精度等进行了测试,得到三个运动方向(横滚、俯仰及偏航)相应的实验数据。测量结果表明:应用该方法测量出的平台角位置测量精度及角位置测量重复性等能够很好地满足六自由度平台的技术指标,为今后进一步开展新的全参数测试方法研究奠定了坚实的基础。

