适应度二次选择的QPSO和SA协同搜索大规模离散优化算法

张兆娟，王万良，唐继军

（1.浙江工业大学计算机科学与技术学院，浙江 杭州 310023；2.天津大学智能与计算学部，天津 300050）

1 引言

近年来，海量数据资源和计算能力的提升对大数据时代网络优化等问题产生巨大影响，传统优化算法难以面对大规模优化问题时搜索空间急剧增长的挑战。针对通信领域，不同的任务调度方式影响数据中心的利用率、能耗和通信网络效果。另一方面，计算智能算法在面对大规模、复杂、高维的优化问题时，优化能力会受到限制。此时，单一算法的优化能力大大削减，但将多种算法协同能够发挥混合算法的效率，从而提升优化的性能[1-2]。

面对大规模、高维数据情形，混合优化策略可用于特征选择、入侵检测、通信网络的优化调度等领域。Gheyas 等[3]提出模拟退火（SA,simulated annealing）和遗传算法（GA,genetic algorithm）的结合算法，可以基于GA 的全局搜索和SA 的避开局部最优能力对大规模的特征子集进行选择。张震等[4]采用遗传算子对粒子群算法进行了改进，并联合禁忌搜索对入侵检测的高维数据特征进行选择。王晟等[5]提出一种基于遗传算法和禁忌搜索算法混合优化的移动代理测量调度方法，用于无线传感器网络中移动代理派遣次序的优化调度。叶苗等[6]结合问题实际背景设计出混合人工蜂群求解算法，对无线传感器网络中新的最小暴露路径问题进行求解。

一个优化算法的性能主要取决于以下4 个方面的能力[7]：较好的全局搜索能力、快速收敛到最优解附近、较好的局部搜索能力、较高的计算效率。面对大规模、高维、离散搜索空间急剧增长的挑战，单一算法的优化能力呈现一定的局限性，协同优化算法能够克服上述不足。由于计算智能算法一般存在早熟现象，因此容易陷入局部最优。计算智能算法主要从初始解的选取和局部最优能力的跳出2 个方面进行改进。

由于种群规模的存在能够增加解的多样性、SA突跳性有助于量子粒子群优化（QPSO,quantum-behaved particle swarm optimization）算法跳出局部最优，本文提出了一种改进的离散量子粒子群和模拟退火协同优化（IDQPSO-SA,improved discrete QPSO combined with SA）算法。IDQPSO-SA引入适应度二次选择机制，使量子粒子群优化算法适合于求解离散优化问题，而且采取镶嵌结构，结合了SA 和QPSO 各自的优点。IDQPSO-SA 的整个搜索包含2 个阶段：先利用QPSO 的并行搜索和保留历史信息能力执行搜索；再将QPSO 搜索的个体最优解作为SA 初始解，利用SA 概率突跳性来提升全局搜索能力。

2 基于适应度二次选择的离散QPSO 和SA协同优化算法

2.1 基于适应度二次选择的全局平均最优位置更新策略

受量子空间中粒子运动的启发，Sun 等[8]于2004 年提出了一种能够保证全局收敛的QPSO 算法。由于QPSO 算法只需控制一个参数，全局搜索能力较强，已广泛应用于网络通信聚类[9]、最优设计等领域[10]。QPSO 算法中平均最优位置的引入能够提升搜索后期粒子跳出局部最优解的概率。但是，由于传统QPSO 算法是针对连续空间设计的，平均最优位置计算方法是直接对所有粒子个体位置进行连续求和再平均而得。因此，已有QPSO 不适合离散工程优化问题。

本文引进适应度二次选择机制，提出一种适用于离散优化问题的全局平均最优位置更新策略。首先，对所有适应度值进行平均，距离平均适应度值位置最近的个体则为初次得到的平均最优位置；然后，选择大于第一次求得的平均适应度值的个体，并和第一次求得的平均适应度值进一步进行平均，得到第二次平均的适应度值；最后，选择距离第二次求得的平均适应度值位置最近的个体，确定为最终平均最优位置。

平均最优位置更新式为

其中，M表示种群数目，f(pbesti)表示个体最优对应的适应度值，cbest 表示第一次选择得到的平均最优位置，f(cbest)表示第一次求得的平均适应度值。

二次选择策略考虑了量子机制的不确定性，并从目标函数的角度提出了全局平均最优位置更新的方法；此外，充分考虑了种群分布带来的影响，即第一次选择将整个种群都进行了平均，并在第二次选择时保留了整个种群较优的个体。综合分析，本文提出的二次选择的更新策略有助于保留整个种群的多样性，也适用于任何离散工程优化问题。

2.2 更新进化流程

步骤1采用个体最优和全局最优位置的保优原则更新局部吸引子。

IDQPSO-SA 中局部吸引子的进化更新采用保优原则，通过交换序列实现迭代更新。针对离散工程优化问题，交换操作是指就维度而言进行个体之间位置的交换，多个交换操作组成了交换序列。局部吸引子更新式为

其中，P id表示局部吸引子，μ表示0～1 的随机数，pbest 表示个体最优位置，gbest 表示整个种群的全局最优，符号“⊕”表示交换pbest 和gbest 的位置。

由于Pid的更新迭代综合考虑了整个种群的局部最优和全局最优，即pbest 和gbest 对整个种群的进化都有影响，从左到右依次对比pbest 和gbest 序列并交换更优维度，可以使Pid向更优的方向进化。

步骤2采用个体和平均最优位置、局部吸引子二次保优原则更新个体位置。

IDQPSO-SA 的个体进化更新主要依据个体位置、平均最优位置、局部吸引子保优原则进行，其中个体位置和平均最优位置分别用Xid和mbest 表示。整个更新过程包含2 个阶段：首先依据mbest 和从左到右交换更优维度得到一个基本交换序列ss1和进化位置Xid，即其中soi表示从Xid到mbest 需要进行的交换算子；然后，根据式，进一步和局部吸引子Pid进行第二次交换。IDQPSO-SA 的个体进化更新式为

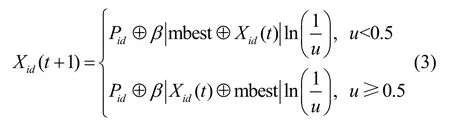
其中，X id(t+1)表示个体当前位置，t表示当前迭代次数，β表示扩张−收缩因子。

步骤3采用SA 嵌入量子粒子群优化算法更新个体。

SA 算法[11]主要依据不可逆动力学的思想，在某一温度下经过不断降温，在全局空间中基于蒙特卡罗（Monte Carlo）迭代启发式随机搜索最优解，同时能以一定概率跳出局部极小值并最终趋于全局最优。由于QPSO 搜索存在进化缓慢、“早熟”、后期易陷入局部最优现象，本文结合SA 和QPSO各自的优点，提出IDQPSO-SA。

SA 是一种根据给定函数利用概率方式获取近似全局最优解的启发式算法，能够通过突跳性来扩大搜索范围和接受较差解，从而避免算法陷入局部最优。传统模拟退火算法若采取随机产生初始解的方式，适应能力较差。IDQPSO-SA 算法采用镶嵌结构，其中模拟退火进行种群更新的主要思路为：在初始阶段，将量子粒子群优化算法搜索得到的个体最优位置作为输入初始解；然后，由状态产生函数产生新个体，利用状态接受函数以一定概率接受新个体，温度按一定比例下降并将该新个体作为下一轮迭代时的当前解；不断迭代直至温度达到终止条件后产生最终解，完成整个IDQPSO-SA 算法的混合搜索。

2.3 IDQPSO-SA 的实现

IDQPSO-SA 中，每个个体分别独立进化，每一次进化促使整个种群更好地适应整个环境。随着迭代的不断进化，搜索到的全局最优解越来越接近理论意义上的最优。当适应度函数评估次数达到终止条件时，整个搜索进程停止；否则，重复搜索直至收敛。本文提出的IDQPSO-SA 算法的流程如图1 所示。

3 基于IDQPSO-SA 的祖先基因推断优化

3.1 祖先基因推断优化问题的研究现状

最近，全球疫情给全世界带来了新的挑战，而对冠状病毒基因组序列进行分析以确定溯源具有非常大的现实意义。事实上，针对新冠病毒溯源分析，即祖先基因推断属于典型的离散工程优化问题。尤其在基因组数据规模扩大时，搜索空间急剧增长的问题日益显著。本文以基因组的推断为背景，探讨大规模离散工程优化问题的协同算法效果。祖先基因推断是系统进化树重建的关键环节，能够为生物学深层进化模式的发现等很多重要问题提供帮助，构建进化树以寻找不同生物的种间同源基因和种内同源基因，广泛应用于生物学、基因组学和病毒学领域，如对冠状病毒基因组序列进行溯源分析、蛋白质和流行性疾病网络结构预测、药物设计等[12-16]。

基于简约方法进行祖先基因推断被广泛研究。2009 年，Xu[17]提出了一种基于充分子图（AS-Median,adequate subgraph median）的分支定界方法，基于子图的迭代贪心搜索求解祖先基因推断优化问题，但适用于小规模数据集。2015 年，Feijão 等[18]提出一种基于中间基因组的系统发育重建算法，能够在保持性能时花费较低的计算成本。另一方面，计算智能由于启发式信息的搜索特点[19]，也被应用于祖先基因推断的研究中。2013 年，Gao 等[20]提出基于遗传算法的祖先基因推断求解算法（GA-Median），GA-Median 主要集成了遗传算法与基因组分类策略来推断祖先基因。进一步，Gao等[21]采用协同进化遗传算法，通过分而治之和共享初始节点集合的策略来提升叶子节点规模增大时祖先基因推断的准确性。Xia 等[22]提出基于模拟退火算法的求解方法（SA-Median），SA-Median的计算成本较低但获取的解性能低于AS-Median和GA-Median。

图1 IDQPSO-SA 算法的流程

面对大规模祖先基因组推断，SA-Median、GA-Median 和 AS-Median 体现出不同特点。SA-Median 具有最低的计算开销，但除时间成本以外的其他性能指标受限。此外，SA-Median 并不具有并行性，进化搜索时由于没有冗余和历史信息从而搜索能力有限。GA-Median 通过生成较多的候选解从而不断进行解的选择来保证所求解质量，但GA-Median 的计算开销太大。AS-Median 的计算开销和存储空间会随着进化事件的增加而快速增长，对硬件配置的要求随基因组规模和距离的增大而急剧上升。以上分析表明，SA-Median、GA-Median和AS-Median 的可扩展性受限，不适用于解决大规模和距离较远的祖先基因推断问题。

针对祖先基因推断应用实例，n个基因序列包含2n n! 个祖先基因组可能性，在大规模、高维、基因组距离较远时整个搜索空间会急剧增长。此时，已有的求解算法在硬件内存、存储空间、计算开销上都面临一定的不足。QPSO 具备较强的全局搜索能力，且SA 由于突跳性能够在一定程度上避开局部最优。因此，本文提出IDQPSO-SA，采用基于平均适应度值的二次选择更新全局平均最优位置的策略，克服传统QPSO 算法无法应用于离散问题的不足，将二次切割与连接（DCJ,double cut joining）排序策略引入IDQPSO-SA 来降低搜索空间大小、提升祖先基因推断的搜索效率。

3.2 基因进化事件与DCJ 操作

基因组由有序的带符号的基因序列组成并表示为{g1,g2,…,gi,…,gj,…,gn}。其中，基因的正向和反向分别由g或−g表示。对于基因gi，头部和尾部分别由表示。正向表示方向从头到尾，而反向则表示方向从尾到头。考虑方向后，基因组可以是线性或圆形（当头和尾重合）形式。

1) 基因组进化事件

基因组进化事件包括倒位（inversion）、转换（transition）、易位（translocation）、裂解（fission）和合并（fission）。采用倒位操作，则该基因组表示为{g1,g2,…,gi−1,−g j,−gj−1,…,−g i,gj+1,…,gn}。假设j＜k，并给定3 个基因序列{g i,g j,gk}，当进行转换操作后则生成一个新的基因组{g1,g2,…,gi−1,gj+1,…,g k−1,gi,…,g j,gk,…,gn}。易位是指当一条染色体的末端断裂时，将其附加到另一条染色体的末端。裂解是指将一条染色体分裂成2 条染色体。合并是指将2 条染色体合并成一条染色体。

如果gi紧随着gj，则定义gi和gj相邻，2 个连续基因的邻接（adjacenc y）具有4 种类型：。此外，当2个基因在一个基因组中相邻但在另一个基因组中不相邻，且该端是末端不与任何其他基因相邻时，则产生断点。

2) DCJ 距离

DCJ 操作由Yancopoulos 等[23]提出，包含了所有基因组进化事件。常见的DCJ 操作包含以下4 种。

DCJ 距离定义为一个基因组转化为另一个基因组所需进行的DCJ 操作数目。不同的DCJ 操作会影响奇数边和环的个数，且会进一步影响邻接图的结构，基于邻接和端的关系构建的邻接关系如图2所示。基因组G1与基因组G2的进化距离为

3) DCJ Median 问题

3 个基因组定义了最小的无根二叉树，祖先基因推断问题定义如下：给定3 个基因组和一个祖先基因组，若能使该祖先基因组到3 个基因组的DCJ距离之和最小化，则该祖先基因组的推断转化为中位基因（Median）问题的求解。因此，祖先基因推断问题称为DCJ Median 问题。如图3 所示，Median到给定3 个基因组的进化距离之和为

图2 2 个基因组的邻接关系

给定3 个基因组G1、G2和G3，G m表示祖先基因组，那么DCJ Median 定义为3 个给定基因组到祖先基因组的距离之和S3的最小值。

图3 DCJ Median 问题

4) DCJ 排序策略

由于n个基因序列包含2n n! 个祖先基因组可能性，若采取穷尽搜索则计算开销较高，随着数据规模的不断增加，搜索空间快速增长的问题日益显著。因此，若只采用IDQPSO-SA 来进行大规模祖先基因离散问题的推断，则会由于计算代价过高而在一段非常长的时间内无法收敛。为了克服计算开销过高的不足，进一步加速搜索进程，本文采用DCJ 排序策略引入IDQPSO-SA 算法来求解DCJ Median 问题（QPSOSA-Median）。

DCJ 距离定义为一个基因组转化为另一个基因组所需进行的DCJ 操作个数，由于不同的DCJ 操作会影响奇数边和环的个数、邻接图的结构，因此不同的DCJ 操作的进化成本不一样。祖先基因的推断作为进化重建的关键，其目标是确立一个Median，其到已给定基因组的进化距离最小。DCJ排序策略的主要思想如下。针对2 个基因组，存在多种不同的DCJ 操作来完成进化，但是不同的DCJ操作求得的进化距离是不一样的。从进化操作出发，选择一条能够提升搜索空间效率的方法，若所求解的祖先基因组刚好位于基因组Gi转化为Gj的路径上，则可以节约搜索空间，从而实现整个进化成本的最小化。该策略被称为DCJ 排序策略。本文采用的DCJ 操作都是指最优DCJ 操作，不包括中性和反最优操作。

3.3 基于QPSOSA-Median 的祖先基因推断

3.3.1 QPSOSA-Median 的初始化

1) 基于DCJ 排序的种群初始化

在QPSOSA-Median 中，整个种群初始化的核心是生成一系列的候选祖先基因组。其中，初始候选解会进一步影响QPSOSA-Median 的性能。高维时搜索空间较大，若随机选择一个候选祖先基因组则可能造成与真正最优的祖先基因进化距离非常远，从而导致搜索很难收敛。为此，在该QPSOSAMedian 中引入DCJ 排序策略。依据从Gi到Gj的距离产生6 个候选Median，然后随机选择一个作为QPSOSA-Median 的初始解。

2) 设定进化成本为适应度函数

在QPSOSA-Median 中，适应度函数反映整个物种进化的好坏，而且物种的适应度值决定是否能够在下一代进化中被保留，其中更优适应度值的物种能够以更大概率在进化过程中生存下来。针对DCJ Median 问题，一种有效的方法是采用进化距离成本MS（median score）作为适应度函数，3 个基因组与候选祖先基因组之间的DCJ 距离成本为

3.3.2 基于DCJ 排序策略的祖先基因组进化更新

1) 基于适应度二次选择的全局平均最优Median 更新

1.4 统计学方法 采用RevMan5.3软件进行数据分析。计量资料采用加权均数差(WMD)或标准化均数差(SMD)进行分析，各效应量均以95%可信区间(CI)表示。对纳入的文献进行异质性检验，若P≥0.05，I2≤50%，则采用固定效应模型进行分析；若P≤0.05，I2≥50%，则采用随机效应模型分析。

假设种群规模为M，并且给定3 个基因组{G1,G2,G3}，候选Media n 基因组总数为M× 6 × 6，因此初始候选基因组中有36M个候选Median 基因组，随机选择一个并计算其到给定的3 个基因组之间的 DCJ 距离。为了提升个体的多样性，QPSOSA-Median 采用的基于适应度二次选择更新平均最优位置的策略是针对整个种群的。首先，对初始候选解的进化距离成本进行平均，保存小于平均进化成本的个体，淘汰大于平均进化成本的个体；然后，对上一轮已经保存个体的进化距离成本第二次求平均；最后，选择与第二次求得的平均进化成本最接近的个体作为全局平均最优祖先基因组。该全局平均最优祖先基因组充分体现了生物基因序列离散化的特点，也反映了整个种群的多样性。

2) 采用DCJ 排序策略和保优原则更新局部吸引子

QPSOSA-Median 算法中采用DCJ 排序策略指引和全局最优位置的保优原则更新局部吸引子。更新过程中，参数μ设为0.5，即局部最优Median 和全局最优Median 具有相同的权重系数。由于DCJ排序策略进行交换和2 个比较基因组之间的目标顺序有关，目标基因组应选取进化距离成本较低的基因组。由于全局最优在任何情况下都不差于个体局部最优，针对局部最优和全局最优的迭代更新过程，从pbest 到gbest 分别以距离产生 6个候选基因组，然后选择最优的一个基因组作为候选局部吸引子Pid。该单次DCJ 排序更新局部吸引子的策略能够确保整个种群都向进化成本最低的方向迭代进化。

3) 采用二次DCJ 排序策略和保优原则更新Median

祖先基因组的更新主要包含2 个阶段，采用个体和平均最优位置、局部吸引子二次保优原则更新个体，并采用DCJ 排序策略指导最优Median 基因组的搜索。在第一个阶段，基于mbest 从左到右将DCJ 排序策略应用于Xid，其中Xid表示当前求得的Median，mbest 表示平均最优候选Median。在第二个阶段，在和Pid之间应用DCJ 排序策略来更新当前Median。此外，为了增强QPSO 的搜索能力，QPSOSA-Median 进一步采用DCJ 排序策略来启发式搜索Median 基因组，从当前候选Median 到3 个给定的基因组之间随机取样，然后从取样中选择一个作为下一代的Median 基因组。

4) 采用IDQPSO-SA 算法更新Median

IDQPSO-SA 算法主要采用镶嵌结构，即将模拟退火算法增加到QPSO 的更新过程中，种群更新的主要思路为：在初始阶段，当QPSO 中所有个体实现了进化更新后，将个体最优Median 作为SA 的初始解；然后，针对所有个体，依据SA 的状态产生函数生成新的个体，状态接受函数以一定概率选择接受新个体；SA 进行退火操作，并将更新后的个体传递到下一轮进行迭代；整个SA不断迭代直至温度达到设定的终止条件，整个IDQPSO-SA 算法的混合搜索完成。此时，全局最优Median 则为整个IDQPSO-SA 算法推断的祖先基因组。

QPSOSA-Median 中，每个物种分别独立进化，每一次进化促使整个生态系统更好地适应整个环境。随着迭代的不断进化，搜索到的全局最优解越来越接近理论意义上的祖先。当适应度函数评估次数达到终止条件时，整个搜索进程停止，否则重复搜索直至收敛。

4 实验结果与分析

4.1 实验环境和参数设置

所有基于计算的智能算法以相同的适应度评估次数为标准，设为300 000 次。其中，GA-Median和AS-Median仅运行一轮，因为基于多次实验经验，GA-Median 和AS-Median 的计算开销较高。虽然种群规模影响QPSOSA-Median 的性能，但影响有限，且基于实验经验，随着种群规模的提升，计算开销显著增加。因此将本文种群规模设为20。参数设置如下：QPSO 最大迭代次数和种群规模分别为1 000和20；SA 算法迭代次数为8 000，初始温度和冷却速率分别为10 和0.9；GA-Median 最大迭代次数为100，每个采样步骤生成50 个基因组。

4.2 QPSOSA-Median 与SA-Median 的性能比较

为了评估QPSOSA-Median 的性能，本文主要考虑以下4 个性能指标：进化成本、求得的Median到真实祖先的进化距离、邻接准确率和运行时间。其中，邻接准确率定义为推断的Median 基因组和真实祖先之间的交集与其并集的比值，即

其中，Acc(Gm,Gt)表示邻接准确率，Gm和Gt分别表示推断的Median 基因组和真实祖先。

QPSOSA-Median 与SA-Median 的性能比较如表1 所示。从表1 可以看出，同SA-Median 相比，随着进化事件个数的增加，本文提出的QPSOSA-Median能够取得较小的进化成本。此外，QPSOSA-Median减少了与真实祖先之间的进化距离，提升了邻接准确率。然而，由于QPSOSA-Median 包含多个独立物种分别进行搜索，计算开销比SA-Median 更加昂贵。此外，同SA-Median 相比，QPSOSA-Median 在大部分情况下性能都较优，且不随进化事件个数的增加而增加计算开销，因为计算开销主要和算法的收敛速度有关，QPSOSA-Median 集成了QPSO 和SA 的混合算法的全局和突跳性的优势更有助于收敛。综上，QPSOSA-Median 同SA-Median 相比，能够提升求解Median 的性能。

4.3 QPSOSA-Median与GA-Median 和AS-Median的性能比较

1) 进化成本

进化成本是所有指标当中最能反映求得的Median 基因组与真实祖先之间的关系的，进化成本较低表示性能更优。QPSOSA-Median、GA-Median和AS-Median 的进化成本比较如表2 所示。对表2结果进行分析可知，QPSOSA-Median 的进化成本最小，AS-Median 次之，GA-Median 最大。进一步地，同AS-Median 进行对比分析，QPSOSA-Median和AS-Median之间的差距随着进化事件个数的增加而逐渐增大。从以上分析可得，QPSOSA-Median非常具有竞争力。

表1 QPSOSA-Median 与SA-Median 的性能比较

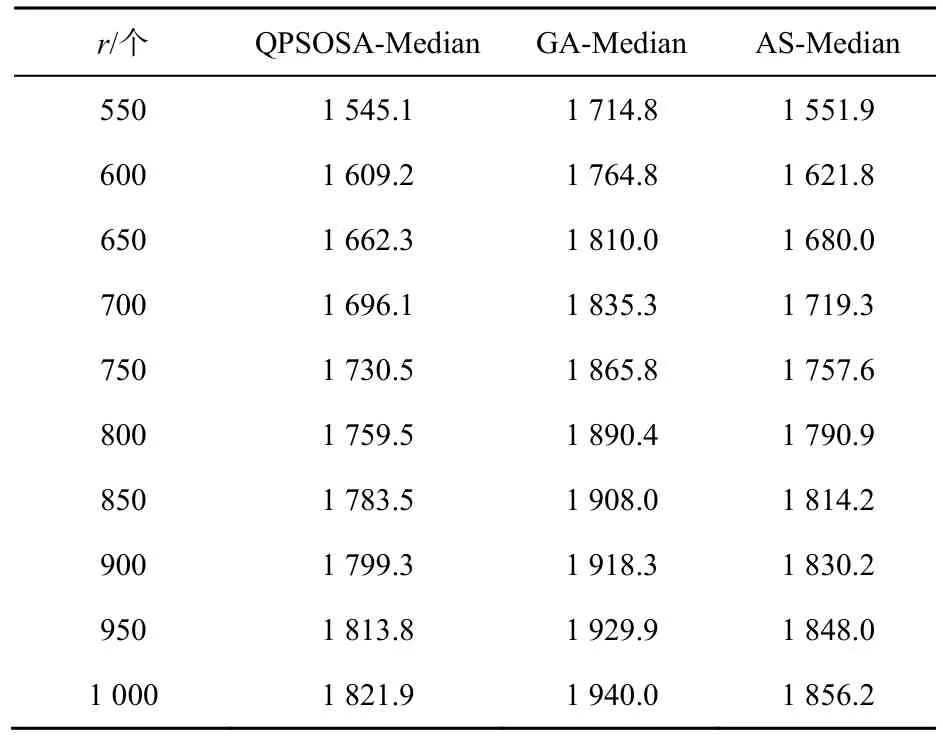
表2 QPSOSA-Median、GA-Median 和AS-Media的进化成本比较

2) 与真实祖先之间的平均进化距离

3种算法推断的Median基因组与真实祖先之间的平均进化距离比较如表3 所示。从表3 可以看出，总体来看，QPSOSA-Median 在不同的基因进化事件数时与真实祖先之间的平均进化距离最小，AS-Median 平均进化距离最大。当进化事件个数为850 和950 时，虽然QPSOSA-Median 求得的Median基因组与真实祖先之间的平均进化距离比GA-Median 大，但是结果和GA-Median 非常接近。此外，在基因组进化事件相对较小时，QPSOSA-Median 所求得的与真实祖先之间的平均进化距离与GA-Median 差距较大。

表3 3 种算法推断的Median 基因组与真实祖先之间的平均进化距离比较

3) 邻接准确率

邻接准确率表示的是祖先基因组与真实祖先之间的交集与并集的比值，邻接准确率越大表明性能 越 好。QPSOSA-Median、GA-Median 和AS-Median 的邻接准确率比较如表4 所示。与GA-Median 和AS-Median 相比，针对不同基因进化事件个数，QPSOSA-Median 获取的邻接准确率优于SA-Median 和GA-Median。此外，在基因进化事件数目小于或等于650 时，GA-Median 最差；但当事件数大于650 时，AS-Median 的性能最差。表4充分表明QPSOSA-Median 在邻接准确率这一指标上具有优越的性能。

表4 QPSOSA-Median、GA-Median 和AS-Median的邻接准确率比较

4) 运行时间

QPSOSA-Median、GA-Median 和AS-Median的运行时间如表5 所示。随着基因进化事件数量的增加，AS-Median 的运行时间急剧增加，当基因进化事件为1 000 时，需要耗费长达40 h。其次，为了统计分析，本文生成20 个实例进行验证，计算一个实例需要耗费10 h 以上，整个实例则需要耗费9 天。GA-Median 的计算代价太高。综合对比，QPSOSA-Median 计算开销比 GA-Median 和AS-Median 低得多。

表5 QPSOSA-Median、GA-Median 和AS-Median 的运行时间

5 结束语

为了解决大规模离散工程优化面临的高维等复杂性难题，本文提出一种结合量子粒子群优化的全局搜索和模拟退火的概率突跳性的协同算法。首先，从目标函数求得的适应度值出发，提出一种基于适应度二次选择的全局平均最优位置更新策略，克服传统QPSO 进化更新方法不适合离散工程优化问题的不足；其次，将 DCJ 排序策略引入IDQPSO-SA 来降低搜索空间大小。通过在大规模且距离较远的不同基因组进化事件的数据集上的实验表明，本文提出的算法同已有算法相比能够取得较好的性能，这进一步表明了本文算法的有效性和稳定性。

尽管IDQPSO-SA 算法在不同的进化事件下进行测试验证了性能，但有许多问题值得进一步研究。例如，将本文提出的改进的协同算法用于对大规模优化问题采用的分布式网络进行调度从而减少能耗；对初始解的选取进行优化和采用分布式计算来降低计算开销；结合计算智能算法中的搜索策略来加速搜索过程；采用深度学习来深度挖掘进化历史，从大数据分析的角度为大规模优化问题提供新的见解等；增加协同算法的实际应用，如对冠状病毒基因组序列进行分析以溯源。