分数阶系统控制下时间优化问题的可解性

练婷婷, 李 刚

(1. 盐城工学院数理学院, 江苏 盐城 224003; 2. 扬州大学数学科学学院, 江苏 扬州 225002)

本文主要讨论如下分数阶微分系统控制下时间优化可行解的存在性:

(1)

其中1<α<2,x(·)取值于Banach空间X, Dα是α阶Caputo分数阶导数,A:D(A)⊆X→X是X上预解{Sα(t)}t≥0的无穷小生成元, 控制函数u(·)取值于可分自反Banach空间Y,B:Y→X为有界线性算子,Uad是满足一定条件的可容许控制集．

1 预备知识

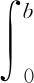
利用拉普拉斯变换, 类似于文献[5]的证明,可得系统(1)的适度解如下:

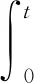
2 主要结果

假设: (H1)A生成的预解{Sα(t)}t>0是紧的, 且按照一致算子拓扑连续, 记M=supt∈J‖Sα(t)‖; (H2)f:J×X→X连续, 且对所有的(t,x)∈J×X存在常数N1>0, 使得‖f(t,x)‖≤N1; (H3)B:Y→X是线性有界算子, 记‖B‖=MB．定义可容许控制集Uad={u∈Lp(J,Y):u(t)∈U(t),a,t∈J}, 其中p>1/α; 集值映射U:J→Pf(Y)(Y中非空闭凸子集的全体)满足条件: (H4)映射U是图像可测的, 且对几乎处处的t∈J, 存在m∈Lp(J,R+)(p>1/α)使得‖U(t)‖=sup{‖μ‖:μ∈U(t)}≤m(t)．根据文献[6], 若此条件满足, 则Uad≠∅, 且易见Uad为Lp(J,Y)中的有界闭凸集．进一步, 对任意u∈Uad, 有 ‖u‖Lp(J)≤‖m‖Lp(J), 且Bu∈Lp(J,X)(p>1/α)．

引理3若以上条件均满足, 则控制系统(1)在区间[0,b]上至少有一个适度解．

证明 利用预解{Sα(t)}t>0及相关算子{Cα(t)}t≥0与{Pα(t)}t≥0的紧性和一致算子拓扑连续性, 结合Schauder不动点定理, 类似于文献[4]中引理3.5的证明可得结论成立．

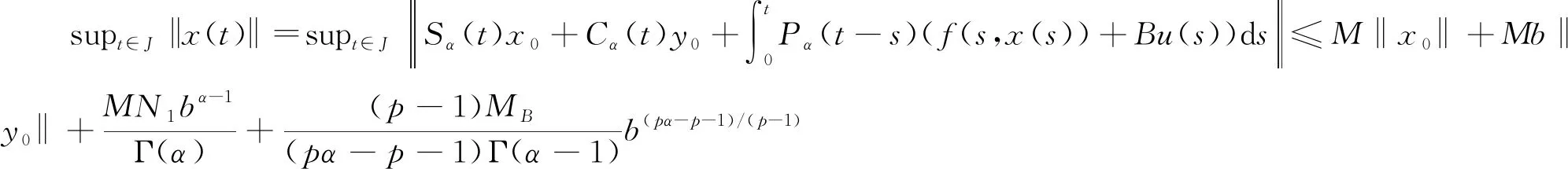
引导基金是由政府设立并按照市场化方式运作的政策性基金，不以营利为目的，通过财政性资金投入，引导社会资本支持科技型企业发展，促进科技成果转化和产业化，全面提升科技型中小企业的创新能力。引导基金的资金来源包括市级财政专项资金，引导基金资金存放银行或者购买国债所得收益，引导基金投资退出返回的本金及收益，个人、企业或者社会机构无偿捐赠的资金等。

定理4若假设条件均满足, 则问题(P)至少存在一个时间优化可行解．

证明 根据引理3, 对任意的u∈Uad, 系统(1)至少存在一个适度解xu∈B(0,R)使得(xu,u)∈Ad,证明过程分为两步:

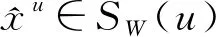
(2)

(3)

(4)

(5)

ii) 根据第一步, 对任意的u∈U0, 问题(P)存在优化时间tu, 令t*=infu∈U0tu,下面将证明存在u*∈U0以及x*∈SW(u*)使得x*(t*)∈W．若集合U0中含有有限个元素, 则结论显然成立; 若否, 则存在非增的时间极小化序列{tun}n≥1使得

limn→∞tun=t*,

(6)

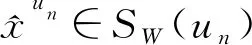
(7)

(8)

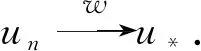
本文通过构造两次时间极小化序列的方法弥补了控制系统适度解存在但不唯一这一不足之处, 进一步减弱了对非线性函数的Lipschitz连续性假设条件．本文的结论改进和推广了文献[3-5,7-10]等相关结果．