基于增强回归树的杉木人工林林分断面积模型研究
臧 颢,黄锦程,刘洪生,欧阳勋志,宁金魁*
(1.江西农业大学 林学院,江西 南昌 330045;2.江西农业大学 鄱阳湖流域森林生态系统保护与修复国家林业和草原局重点实验室,江西 南昌 330045;3.江西省崇义县林业局,江西 赣州 341300)
【研究意义】杉木(Cunninghamia lanceolata(Lamb.)Hook.)是我国最重要的用材树种之一。据第9 次全国森林资源清查结果[1],杉木人工林总面积达990.20 万hm2、蓄积为7.55 亿m3,占全国人工林总面积的17.33%和总蓄积的22.30%。林分断面积是林业调查中的主要因子以及林分生长和收获预估体系中的重要变量[2-3],因而,研究杉木林分断面积生长对预估杉木林的收获有重要意义。【前人研究进展】为了构建林分断面积模型,一些学者采用多种统计方法进行了研究。基于江西省11 块样地数据,杜纪山等[4]采用Richards 和Schumacher 方程作为基础模型,以年龄、林分密度指标和立地质量指标为自变量构建了杉木林分断面积生长模型,并采用最小二乘法估计了模型参数。倪成才等[5]基于美国佐治亚州148 个火炬松人工林固定样地的调查数据,采用代数差分方程构建了林分断面积模型,并采用最大似然和限制性最大似然估计了模型的参数。Zhao 等[6]收集了江西省、广东省和广西省共583 个杉木人工林固定样地数据,采用最小二乘法和3 水平混合效应模型对含优势高和每公顷株数的林分断面积生长模型进行了参数估计。Zhang 等[7]以江西省分宜县杉木人工林为研究对象,采用贝叶斯模型平均法将林分模型、单木模型和直径分布模型联合起来,并对林分断面积进行了预测。张雄清等[8]采用广义代数差分法构建杉木林分断面积生长模型,并采用最小二乘法和贝叶斯法分别估计了模型参数。【本研究切入点】尽管最小二乘法、混合效应模型、贝叶斯等方法被广泛用于构建林分断面积生长模型,但这些统计方法在应用时都存在着一定的假设前提,诸如参数的特定分布形式、自变量的独立性等,且需要预先给定因变量和自变量之间的关系式[9-11]。而森林的生长是一个复杂的过程,它受到立地条件[12-14]、气候变化[15-16]、林分结构[17-18]及其交互作用的综合影响,因而上述假设通常难以满足[19]。由于能处理复杂的变量关系,且不需要预设模型的形式和输入数据的分布等优点[20-21],近些年来,机器学习被逐渐用于模拟森林生长模型中,而增强回归树作为机器学习的一种,其预估精度较高且估计结果比较稳定[22-24],因而在林业上有着较多的应用。【拟解决的关键问题】本研究以江西省崇义县杉木人工林为研究对象,采用增强回归树构建杉木人工林林分断面积生长模型,探讨了增强回归树算法中不同参数的变化对模型的影响,并分析了不同林分密度指标和不同立地指标及其交互作用对林分断面积的模拟影响。
1 研究区概况
研究区位于江西省赣州市崇义县,属于南岭的北端。崇义县的地理坐标为113°55′E~114°38′E,25°24′N~25°55′N。全县属亚热带季风气候,年平均气温17.9 ℃,极端最高39.9 ℃,最低-8 ℃,年均降水量1 603.1 mm,无霜期307 d。全县总面积2 206.27 km2,主要地貌为低山、丘陵,土壤类型有黄壤、红壤等。崇义县属常绿阔叶林生物气候带,主要树种有丝栗栲(Castanopsis fargesiiFranch.)、米槠(Castanopsis carlesii(Hemsl.)Hayata)、杉木(Cunninghamia lanceolata(Lamb.)Hook.)、马尾松(Pinus massonianaLamb.)、苦楝(Melia azedarachL.)、南酸枣(Choerospondias axillaris(Roxb.)Burtt.et Hill)等。
2 材料与方法
2.1 数据来源
数据来源于2016 年江西省赣州市崇义县的森林资源二类调查数据,本研究选择了起源为人工且优势树种为杉木的乔木林小班进行分析,共计8 780个小班,主要因子统计信息见表1。
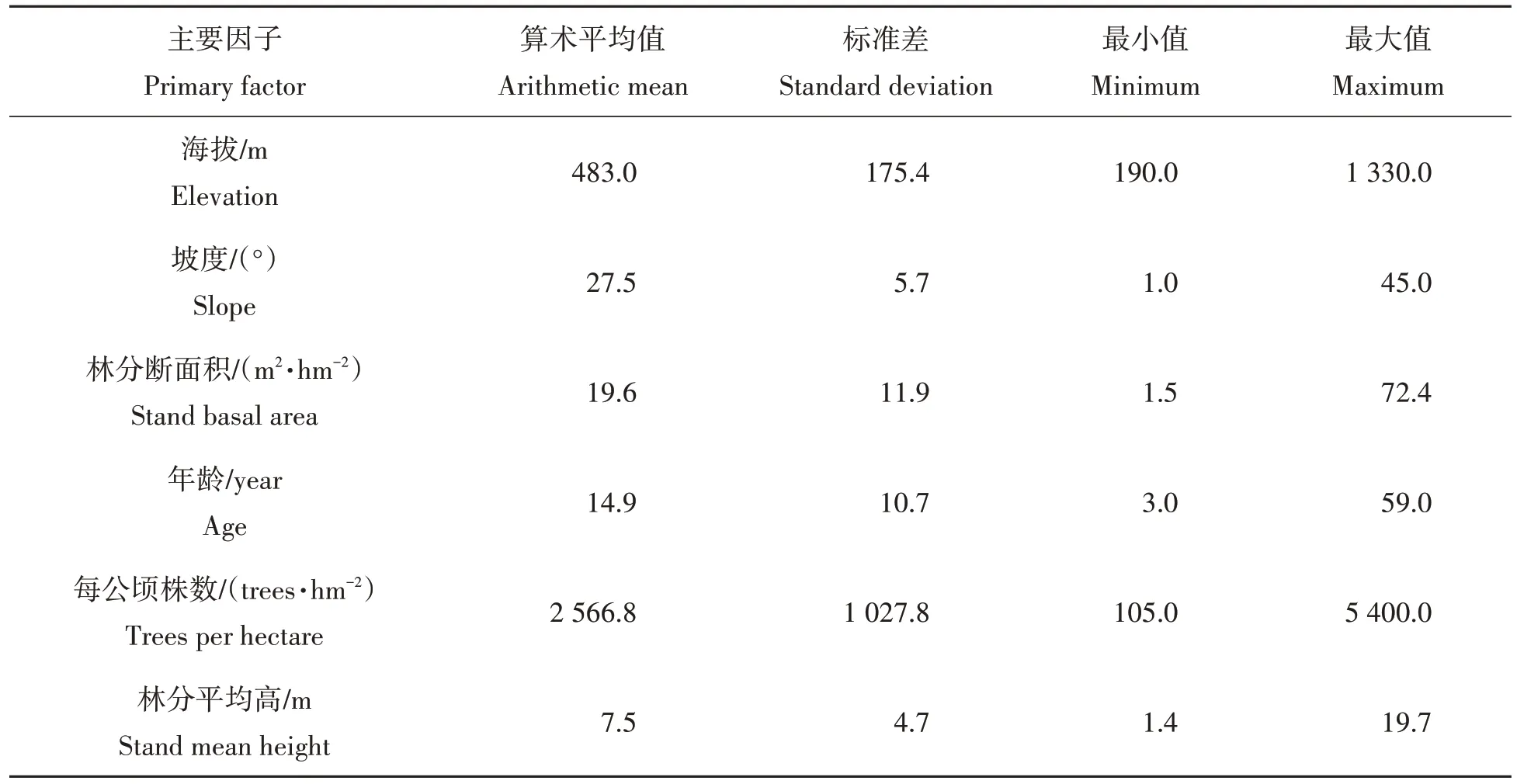
表1 主要因子统计Tab.1 Summary statistics of primary factors
2.2 研究方法
2.2.1 确定自变量 基于前人的研究结果[25-27],立地、密度和年龄是林分断面积的主要影响因子。因此,本研究的自变量也按这3方面进行选择,其中,立地指标选取了地位指数和地位级指数,密度指标选取了每公顷株数和林分密度指数,年龄为平均年龄。地位级指数、地位指数和林分密度指数的计算如下:
(1)地位指数。依据蔡学林等[28]对赣南山地杉木人工林构建的数量化地位指数模型和小班的地形因子信息,计算各小班的地位指数,基准年龄为20 a。
(2)地位级指数。地位级指数是基准年龄下的林分平均高,可采用差分方程进行计算[29]。计算步骤为:1)采用理论生长方程构建林分平均高模型,如式①;2)假定立地条件的高低仅影响林分平均高所能达到的最大值,即方程中反映理论最大值的参数为自由参数,此时,年龄取基准年龄则方程计算得到的就是地位级指数,如式②所示,进而可采用差分方程对该参数进行差分,最终形式如式③所示。

式中,Hi和ti分别表示第i个小班的林分平均高和年龄,SCIi表示第i个小班的地位级指数,t0为基准年龄,本研究中取20年,β0为反映理论最大值的参数,βj为其他待估参数,β0i表示随小班立地条件变化的自由参数,f()表示理论方程,g()表示对应的差分方程。
本研究中选取了常见的理论生长方程[30],各方程形式如下:

式中,β1、β2为待估参数,其他符号如上所述。
(3)林分密度指数。依据Reineke[31]给出的公式计算各小班的林分密度指数,计算公式如下:

式中:SDIi、Ni和Dgi为第i个小班的林分密度指数、每公顷株数和林分平均胸径,D0表示标准平均直径,本研究中取25 cm[32]。
Pretzsch 等[33]通过对欧洲中部的4 种森林类型进行分析,发现树木的径向生长会受到立地和密度的交互作用影响,这一影响随树种的变化而变化,因此,本研究在构建林分断面积模型时考虑了不同立地指标和不同密度指标的交互作用,并于不考虑交互作用的模型进行对比,以判断立地和密度的交互作用对杉木人工林林分断面积的影响。通过8种自变量组合(如表2所示),分别模拟林分断面积,构成8种模型,以模型的模拟效果对立地指标、密度指标及交互作用的影响。
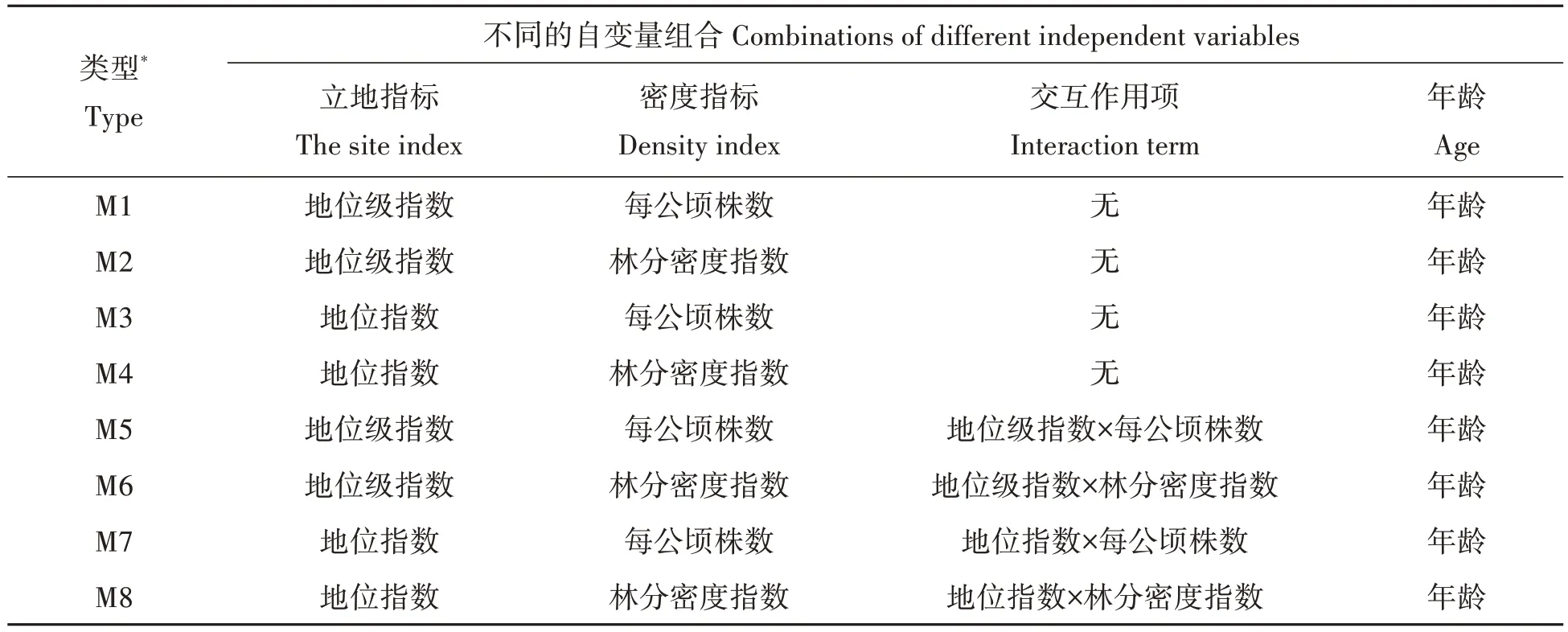
表2 不同的自变量组合Tab.2 Combinations of different independent variables
2.2.2 增强回归树构建林分断面积模型 增强回归树是一种基于集成学习的决策树模型,通过对训练样本进行多次不放回随机抽样,生成一系列训练子样本,并用回归树对每一个子样本进行拟合,拟合过程按顺序进行,将当前的模型添加到之前的模型中,该过程一直持续到指定的迭代次数为止,最终的预测结果则依据各回归树拟合效果进行加权[11,24]。
增强回归树建模有5 个输入参数需要设定,分别为损失函数(distribution)、交互深度(interaction.depth)、收缩参数(shrinkage)、回归树数量(n.trees)、子取样比例(bag.fraction)。针对回归问题,损失函数一般设为平方误差。结合前人的研究结果[24,34],子取样比例取0.5。而交互深度、收缩参数和回归树数量的确定,不同的研究中无统一的结果[11,21,24]。为探讨交互深度、收缩参数和回归树的数量的设置对拟合结果的影响,本研究中对这3个参数设置不同的数值,通过对比不同数值组合的模型评价指标,对模型进行优化:交互深度取1、2、3、4、5、6、7、8、9、10,收缩参数取0.1、0.05、0.01、0.005、0.001,回归树的数量取100、200、300、400、500、600、700、800、900、1000。
2.2.3 模型评价 本研究采用5折交叉验证进行模型评价:1)将数据随机分成5个子样本;2)每次用其中4个子样本作为建模样本,最后1个子样本作为检验样本,依据检验样本计算评价指标;3)重复上一步,直到5个子样本都进行了模型检验;4)计算5次模型检验得到的评价指标的平均值,并以此判断模型优劣。
采用3种指标评价模型的预估精度:MAB,平均绝对误差;RMA,平均相对误差绝对值;RMSE,均方根误差,计算公式如下[21,35-36]:

式中,Gi和分别表示第i个小班的林分断面积实测值和预测值,n为样本数。
本研究中的所有计算均在R 软件中完成,其中,增强回归树调用“gbm”包中的“gbm”函数实现的,增强回归树的参数优化是在“caret”包中的“train”函数实现的。
3 结果与分析
3.1 地位级指数的计算
由表3可知,7种理论方程拟合的效果差异不大,其中,式⑩拟合的林分平均高效果最好。相较其他6 种理论方程,式⑩的MAB减少了0.06%~7.22%,RMSE减少了0.01%~3.91%,因此选择式⑩基础模型构建差分方程,并计算地位级指数。计算地位级指数的差分形式如下:

式中各符号如前所述。
3.2 增强回归树参数优化
图1 显示了8 种林分断面积模型的参数优化情况。总的来看,随着回归树数量的增加,8 种模型的MAB、RMA和RMSE均呈现减小的趋势。这一趋势在不同交互深度下没有明显差异,但随着收缩参数增加,这一趋势逐渐减弱,当收缩参数取0.05 和0.1 时,随着回归树数量的增加,MAB、RMA和RMSE的变化无明显趋势。
综合考虑MAB、RMA和RMSE,8 种模型的最优参数值及其交叉验证的评价指标见表4。可知:含有林分密度指数的模型明显优于含有每公顷株数的模型,含有林分密度指数的模型的MAB减少了80.05%~84.15%,RMA减少了80.42%~84.66%,RMSE减少了77.94%~82.27%;含有地位级指数的模型优于含有地位指数的模型,含有地位级指数的模型的MAB减少了11.32%~25.84%,RMA减少了11.68%~22.96%,RMSE 减少了6.95%~25.24%;含有立地和密度交互作用的模型略优于不含交互作用的模型,含交互作用的模型的MAB减少了4.56%~12.48%,RMA减少了5.88%~15.48%,RMSE减少了1.07%~9.34%,仅M3(地位指数与每公顷株数的无交互模型)优于M7(地位指数与每公顷株数的有交互模型)。M6(考虑了地位级指数、林分密度指数及其交互作用)的各项评价指标均为最小,可用于预估崇义县杉木人工林林分断面积。
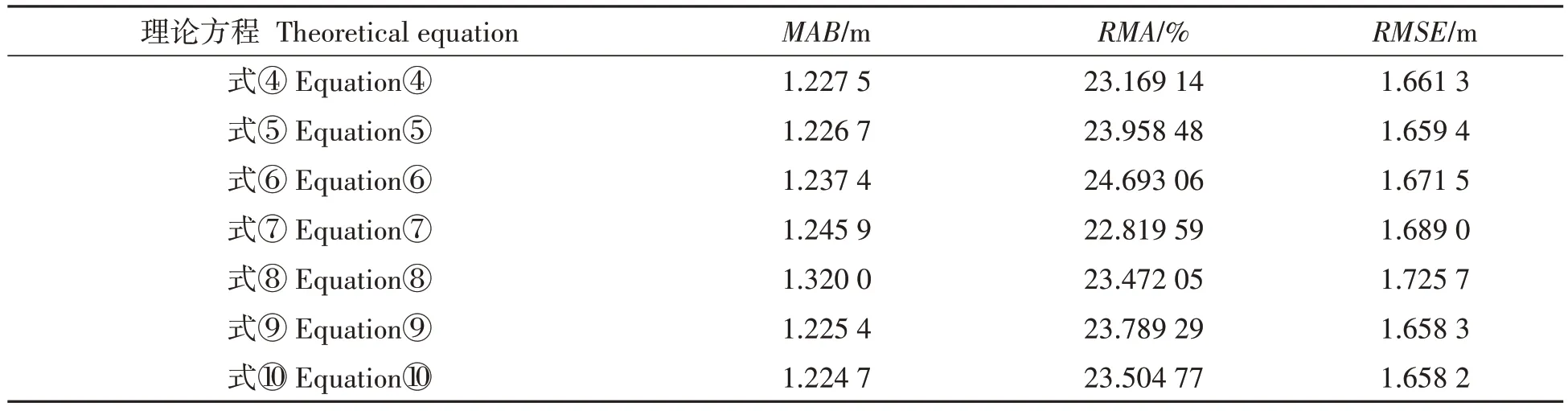
表3 基于交叉验证的林分平均高模型评价Tab.3 The evaluation of stand mean height model using cross-validation
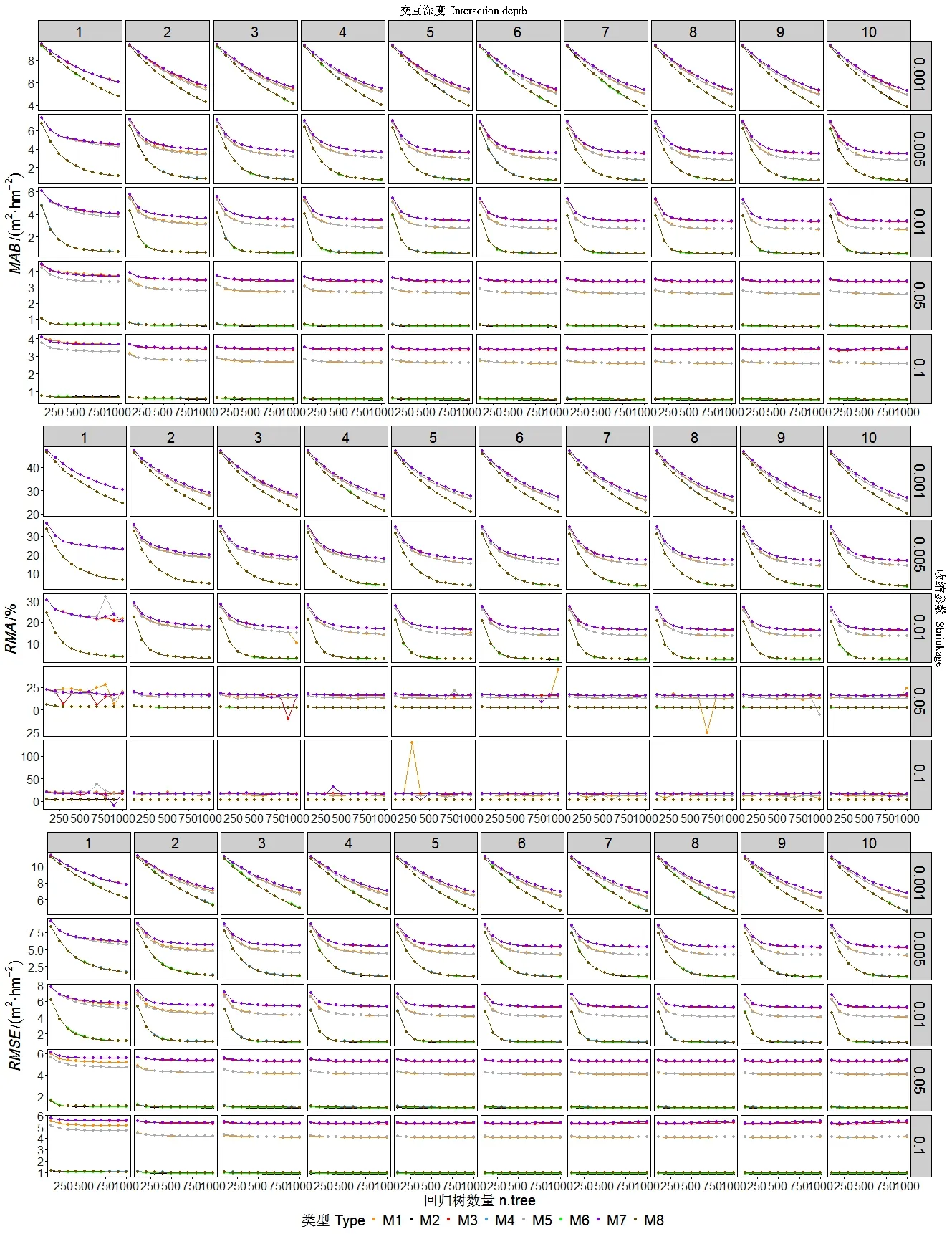
图1 8种林分断面积模型的增强回归树参数优化Fig.1 Tuning boosted regression tree for 8 stand basal area models
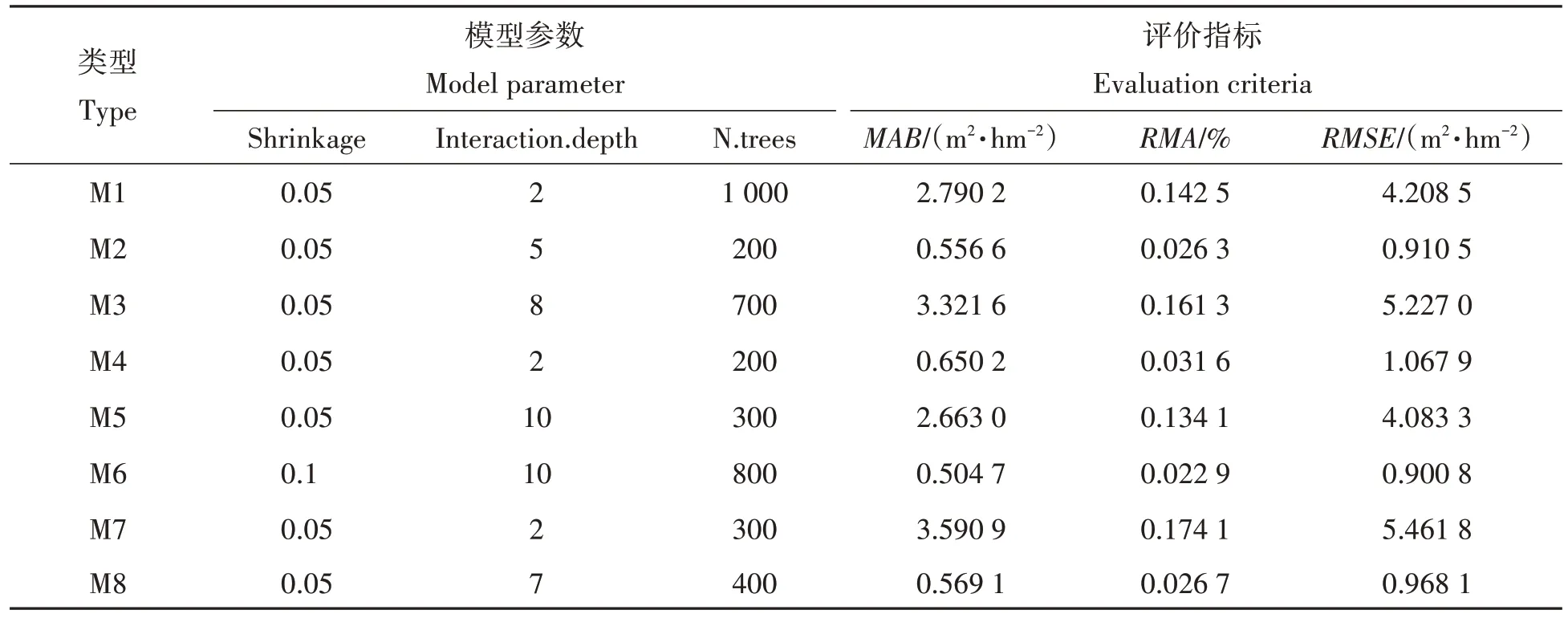
表4 8种林分断面积模型的参数优化结果Tab.4 The tuning results for 8 stand basal area models
4 结论与讨论
本研究以江西省崇义县的杉木人工林为对象,采用增强回归树构建了林分断面积模型,通过交叉验证分析了不同立地指标、不同密度指标及其交互作用对模拟的影响。研究发现,经过参数优化的增强回归树能较好的拟合林分断面积,最优模型的MAB为0.504 7 m2/hm2,RMA为2.29%,RMSE为0.900 8 m2/hm2。
地位指数是基准年龄时的优势高[37],被广泛应用于林分断面积模型中以反映立地质量对林分断面积的影响[4,9,27]。因为连续调查固定样地数据通常缺乏林分优势高数据,只有林分平均高数据[38-39],因此有学者使用基于林分平均高计算的地位级指数评价立地质量[29]。同时,也有学者研究发现林分平均高和优势高之间存在着相当稳定的数量关系[40-41],因而使用基于林分平均高的地位级指数反映立地质量是一种可行的方法。本研究对比了地位指数和地位级指数对林分断面积模拟的效果,发现地位级指数对林分断面积的模拟效果良好,这说明用基于林分平均高的地位级指数能有效的反映立地质量对林分断面积的影响。此外,尽管本研究中,地位级指数对林分断面积的模拟优于地位指数,这可能是因为本研究是采用前人构建的模型推算得到的地位指数,即存在着一定的误差,进而影响了地位指数对林分断面积的模拟效果。
每公顷株数和林分密度指数是被广泛应用于森林生长收获模型中[17,42-43],本研究对比了每公顷株数和林分密度指数对杉木人工林林分断面积的模拟效果,结果显示林分密度指数对林分断面积的模拟效果明显优于每公顷株数,这与一些学者的研究结果相同[9,27]。尽管每公顷株数描述了单位面积上的林木株数,但却没有包含树木大小信息,随着树木的径向生长,可能存在每公顷株数较少但由于树木胸径较大,导致树木个体之间竞争更强的情况,这在一定程度上也会影响到林分断面积的生长。林分密度指数则是将当前的株数转换到标准胸径下的株数,即考虑了林分平均胸径的影响,这可能是林分密度指数的模拟效果优于每公顷株数的原因。
为了探讨立地和竞争是否存在对林分断面积的交互作用,本研究对比了含交互作用项与不含交互作用项的林分断面积模型的模拟效果,结果显示,除含地位指数和每公顷株数的交互作用项的模型外,其余含交互作用项的林分断面积模型拟合精度均略高于不含交互作用项的模型,这说明了立地和林分密度的交互作用对杉木人工林林分断面积有一定影响。这与Pretzsch 等[33]的研究发现类似。因此,如果需要精确模拟森林的径向生长时,有必要考虑立地和林分密度的交互作用。
由于机器学习算法对模型的形式和输入数据的分布没有假设前提,且能处理复杂的变量关系、拟合效果好[11,20],所以逐渐应用于森林生长收获预估中。但也有学者认为机器学习存在“黑箱”问题,无法给出因变量和自变量的关系式,但其实每种机器学习算法存在各自的工作原理,而因变量和自变量的关系也可以通过模拟的方式给出,偏依赖图也可以给出各自变量对因变量的重要性[21]。相对传统的统计方法更关注于模型的基本形式(线性、非线性等)和变量的关系(是否存在共线性、自变量参数是否显著)等问题,采用机器学习方法构建森林生长模型时需要更多的考虑参数值的确定和过拟合问题,参数值的确定可以通过对比不同参数取值组合的拟合效果来确定,但过于追求拟合效果也可能会导致过拟合问题,即对建模样本较好,但在检验样本表现较差的情况[11],因此建议使用机器学习构建模型时需要进行模型检验。
综上所述,增强回归树作为一种机器学习算法,可应用于林分断面积模型的构建,不同的交互深度、收缩参数及回归树数量对拟合精度影响较大,有必要进行参数优化,同时不同的自变量组合对拟合精度也有较大的影响,基于林分平均高的地位级指数和林分密度指数及其交互作用可作为模型自变量以提高模型的预测效果。

