车轮廓形的演变对道岔区轮轨接触几何的影响

钱 瑶，王 平，赵思琪，徐井芒，方嘉晟，王树国

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031; 2. 西南交通大学 土木工程学院，四川 成都 610031; 3.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081)

轮轨几何是研究轮轨接触力学、轮轨动力学的前提和基础[1]。道岔是重要的轨道设备，也是交通运输不可或缺的关键构件。道岔钢轨沿轨道纵向变化会导致道岔的结构不平顺，这种不平顺使道岔区轮轨接触关系较区间更加多变。列车过岔时，车辆与道岔通过轮轨接触几何关系来传递其间动态的相互作用[2-4]。随着我国铁路运输需求的增大、列车运行速度不断提高，车轮型面随服役时间的增大而不断改变。车轮型面的改变势必会引起轮轨间几何关系以及几何参数发生变化，导致轮轨接触关系和轮轨动态相互作用发生较大变化，影响旅客舒适度和道岔的使用寿命，以及使铁路运营成本增大[5-7]。

国内外专家学者针对道岔区轮轨接触几何关系做了大量研究。道岔区结构复杂，尖轨、心轨等钢轨截面不断变化，专家学者们为求解其轮轨接触关系提出了多种数值分析方法。Sugiyama等[8]提出一种能得到道岔纵向任意断面轮轨接触点准确分布情况的数值分析方法；美国的Shu等[9]改进了NUCARS软件的功能，给出一种能更加精确地模拟道岔区轮轨接触情况的模型。我国的任尊松等[10-11]利用迹线法的原理发展成轮轨多点接触算法，避开了复杂的赫兹或非赫兹接触计算过程。赵卫华[12]、曹洋[13]等结合道岔特点将迹线法引入到道岔中。王平[14]基于道岔的结构特征提出了利用迹线法以及有限元理论研究不同磨耗的车轮对轮轨接触几何关系、接触应力等的影响规律的方法。上述成果对道岔区的轮轨接触几何的深入研究起到了至关重要的作用。由于道岔区轮轨相互作用较区间线路更加剧烈，道岔区轮轨接触几何受车轮廓形演变的影响更为敏感，进而改变轮对运动姿态，导致轮轨磨耗加剧，从而影响道岔使用的安全性。因此，研究由于运营里程的变化引起的不同程度的磨耗量下车轮型面对轮轨接触几何的影响，可为我国道岔廓形优化设计以及钢轨打磨提供理论基础。

本文以18号道岔转辙器区钢轨廓形与不同服役阶段的车轮型面匹配为例，基于考虑道岔区变截面特点的轮轨接触几何算法——法向切割法，运用Matlab软件计算车轮廓形与道岔转辙器区钢轨匹配时的轮轨接触点对分布、结构不平顺、滚动圆半径差和侧滚角，以此分析车轮型面磨耗的演变对轮轨接触几何的影响。

1 法向切割法

法向切割法是一种考虑道岔结构特点的接触结合算法，其利用二分法基于左右轮轨同时接触的原理，建立移动窗基于先验经验法求解道岔区的轮轨接触点。

1.1 轮轨廓形的确定

计算轮轨空间几何时，首先要将车轮型面与钢轨廓形的数据进行离散。因此，必须保证所选廓形数据的精确性达到要求。

1.1.1 车轮廓形

车轮体可看做是一个二维车轮型面绕着车轮轴旋转一圈得到的三维曲面，如图1所示。因此，本文将垂直于车轮坐标系平面x′=0的二维车轮型面称为主轮廓线，其上任意点在车轮坐标系中的坐标为[0,y0,z0]T。而车轮体上任意一条轮廓线可以用该轮廓线与车轮坐标系平面的夹角及主轮廓线进行表示，如图1所示。通过研究发现，在轮对出现摇头角时，即使是最不利的情况，只需要扫描车轮踏面的主轮廓线两侧法向角度[αa,αb]以内的区域，就可以找到所有接触点。利用过车轮坐标系原点，与平面x′=0形成[αa,αb]范围内对车轮沿法切割将其均分成n份，加上主轮廓线共有n+1条轮廓线。第i条轮廓线上的点可表示为

(1)

以轮对质心为原点，x轴指向轮对前进方向，建立轮对坐标系，给定轮对参数，将各条轮廓线上的点的坐标转换到轮对坐标系下，第i条轮廓线上的点在轮对坐标系中可表示为

(2)

式中：m为轴心到名义滚动圆的距离。

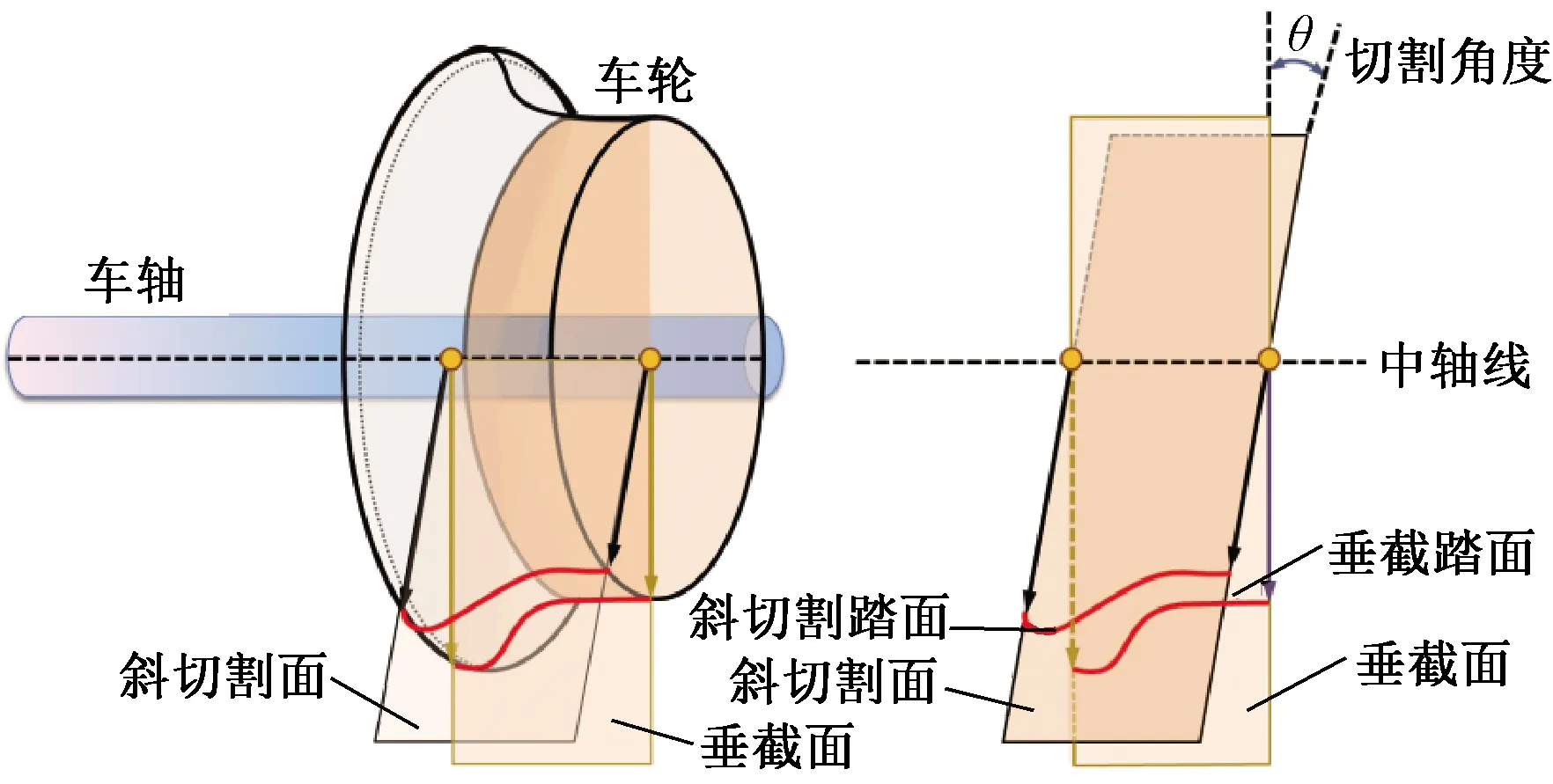
图1 车轮切割图

1.1.2 钢轨廓形

理想条件下基本轨侧廓形同区间线路一样，在沿线路的纵向上不会发生改变，故仅需一组廓形数据进行计算。而对于尖轨侧廓形，其钢轨截面变化使其廓形沿线路纵向发生改变，必须利用合适的曲线模拟钢轨踏面坐标，才能得到符合实际情况的廓形数据。本文的控制断面主要采用三次样条曲线模拟得到，非控制断面通过对控制断面间进行两两线性插值得到。

(1)基本轨侧钢轨

假设钢轨是一个柱状体，所有垂直于轨道中心线的平面切割钢轨所得的廓形线都一样，则钢轨在轨道坐标系中任意xi位置所得的在OYZ平面上的廓形都是一样的。为了获得与车轮上的点一一对应的钢轨廓形坐标，利用车轮在OYZ坐标系中的点插值拟合得到钢轨廓形数据。

(2)尖轨侧钢轨

道岔区尖轨侧转辙器和辙叉部分尖轨和心轨由宽度及高度渐变的特殊变截面钢轨组成，其高度及宽度是随着线路纵坐标逐渐变化的。在计算轮轨接触点时，由于道岔变截面特点，在确定的横移量下，道岔区的轮轨接触点沿线路纵向钢轨廓形的变化而变化。因此，要精确描述道岔区轮轨几何接触状态，需先精确描述道岔廓形沿线路纵向分布规律。

标准的道岔设计图中一般只提供几个关键部位的尖轨、心轨截面。对于标准的18号道岔，可借助CAD绘图软件自动提取坐标点功能，从标准CAD设计图中提取尖轨、心轨的一些关键断面廓形数据。若针对磨耗后或打磨后的道岔，则利用Miniprof轮轨廓形仪在沿线路纵向间隔一定距离进行关键断面廓形采集。利用Matlab软件，利用三次样条曲线模拟控制断面，再利用控制断面线性插值得到非控制断面，如图2所示，最终得到尖轨侧变截面廓形在轨道坐标系中的点的集合。

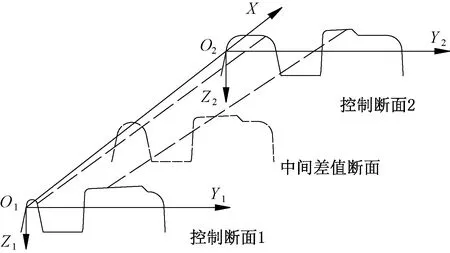
图2 变截面钢轨处理方法

1.2 法向切割法的基本原理

在利用法向切割法计算轮轨几何接触点时，必须先进行如下假设：①轮对和钢轨都是刚体，即两者不会发生弹性变形；②左侧轮轨和右侧轮轨同时接触，且左右接触点处的轮轨间的垂向距离最小。基于上述假设，根据1.1节将可能接触到的车轮曲面表示为若干条空间曲线，将道岔钢轨廓形表示为由若干点组合成的空间曲面，从而将空间曲面与空间曲面的接触问题转换为空间曲线与空间曲面的问题。具体步骤为：

(1)给定初始的左右侧车轮法向切割角[αa_l,αb_l]、[αa_r,αb_r]，将左右侧的车轮面在该范围内均分为n+1条轮廓线。

(2)已知摇头角δ和横移量yw，假设侧滚角θ，将轮对坐标系OwXwYwZw上的车轮离散点投影到轨道坐标系OXYZ，左右车轮离散点在轨道坐标系中可表示为[Xwi_l,Ywi_l,Zwi_l]T、[Xwi_r,Ywi_r,Zwi_r]T。

(3)

(3)基本轨侧的钢轨廓形是沿轨道纵向的拉伸体，即在轨道任意Xri_l处的截面均相同，故其在轨道坐标系中任意Xri_l处的离散点的集合均为[Yr_l,Zr_l]T。

(4)假设尖轨侧为轮轨接触的右侧，利用关键断面间两两线性差值得到尖轨侧变截面钢轨廓形在轨道坐标系中的离散点，在轨道坐标系中任意Xri_r处的离散点的集合为[Yri_rj,Zri_rj]T。

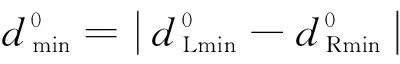
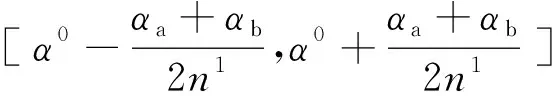
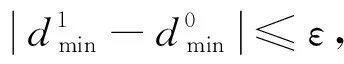
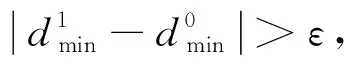
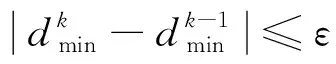
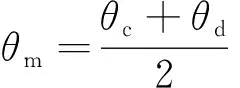
① 若f(θm)=0，即在确定δ和yw的情况下，当θ=θm时，车轮与钢轨正好接触。

② 若f(θm)≠0，即在确定δ和yw的情况下，当θ=θm时，车轮与钢轨未发生接触，此时，若f(θc)·f(θm)>0，则θc=θm；若f(θc)·f(θm)<0，则θd=θm。通过循环迭代，使得|θc-θd|<ε，当侧滚角为θm时，车轮与钢轨正好接触。

由此得到在给定的摇头和横移情况，轮轨接触时的法向切割角及车轮接触点的坐标，从而也得到了钢轨上的接触点坐标。

1.3 基于移动窗的轮轨接触点快速算法

在1.2节中详细说明了法向切割法的计算步骤及假设条件。该方法适用于任意轮轨截面，不局限于等截面钢轨廓形情况。当车轮无摇头时，此时车轮上的轮轨接触点即在主轮廓线上，而钢轨上的轮轨接触点也在主轮廓线所切的钢轨截面上。此时，在搜寻左右轮轨最小距离时，根据主车轮线上的离散点在轨道坐标系中Y方向的集合Yw_l、Yw_r，利用一维三次样条插值函数对钢轨截面进行插值得到钢轨截面在轨道坐标系中与Yw_l、Yw_r一一对应的Yr_l、Yr_r，从而搜寻左右轮轨最小距离，利用二分法原理得到左右轮轨接触点。

若车轮发生摇头运动，车轮上的轮轨接触点不一定在主轮廓线上，因此需要考虑切割车轮线。由于基本轨侧的钢轨具有等截面的特点，其最小距离可以通过一维三次样条插值法将车轮与钢轨的一一对应搜寻得到；但尖轨侧由于钢轨变截面特点，钢轨截面随轨道纵向发生变化，故该侧的钢轨Z轴坐标需要用曲面插值法插值得到。为保证计算结果的精确性，要得到不同车轮姿态下的轮轨最小距离，需将可能接触范围内的车轮曲面用间距很小的轮廓线表示，并对曲面进行多次插值，这将导致计算速度变慢。本文提出一种可以提高速度的方法，在先验经验法的基础上，认为在轮对摇头角的变化幅度较小且保持其他条件不变时，得到的轮轨接触点位置的变化不大，接触参数(如侧滚角等)的变化范围也不大。

(1)当轮对无摇头时，轮轨接触点在主轮廓线及该主轮廓线所切的钢轨截面上，根据法向切割法，利用二分法原理得到不同的横移量下轮轨接触点、测滚角等轮轨接触参数。

(2)当轮对摇头角为0.5°时，认为在相同的轮对横移下，车轮和钢轨上的轮轨接触点的位置、接触参数等在轮对无摇头时的轮轨接触点位置附近，接触参数改变也较小。故在摇头角为0.5°时，以摇头角为零时的测滚角为初始测滚角，截取摇头角为零时的尖轨侧的轮轨接触点位置附近的道岔曲面作为搜寻轮轨接触点的范围，运用法向切割法计算得到轮对摇头角为0.5°时的轮轨接触参数。

(3)在计算轮对摇头角在0°～5°(或-5°～0°)范围内且每间隔0.5°变化一次时，在不同横移量下的轮轨接触点，基于相邻轮对摇头角下所计算出的轮轨参数值进行道岔区曲面插值范围的预测和初始测滚角的确定，采用法向切割法快速计算出轮轨接触点。

1.4 法向切割法的验证

目前，我国运用较多的轮轨几何接触算法是迹线法，其基本假设是在沿轨道纵向上钢轨廓形不发生变化，若将其运用到道岔区轮轨接触几何的计算，该假设不符合实际上钢轨廓形的变化，故其计算结果可能会存在误差。当轮对摇头角不为零时，车轮上的轮轨接触点可能不在主轮廓线上，而钢轨上的轮轨接触点也可能不在主轮廓线对应的钢轨截面上。此时，若采用迹线法计算轮轨接触点，结果会与实际情况有一定误差。

因此，本节中以名义滚动圆半径为430 mm的标准高速车轮LMA车轮与中国高速铁路常用的350 km/h的18号道岔的顶宽15 mm的直尖轨匹配为例，分别采用法向切割法和迹线法计算道岔区轮轨几何接触点，并对计算结果进行对比分析，以验证法向切割法的准确性和必要性。其中，车轮的名义滚动圆半径为430 mm；轮对内侧距为1 353 mm，轨距为1 435 mm。

(1)法向切割法和迹线法的结果对比(轮对无摇头)

如图3所示，通过对比轮对无摇头的情况下，两种算法计算的顶宽15 mm直尖轨与LMA车轮匹配时,不同轮对横移下的轮轨接触点对分布在钢轨X、Y、Z三个方向上的差值可知，三个方向上的轮轨接触点的差值均在±0.1 mm范围内，在允许的计算误差范围内，这说明两种算法所计算的摇头角为零时的轮轨接触点几乎一致，验证了法向切割法的正确性。

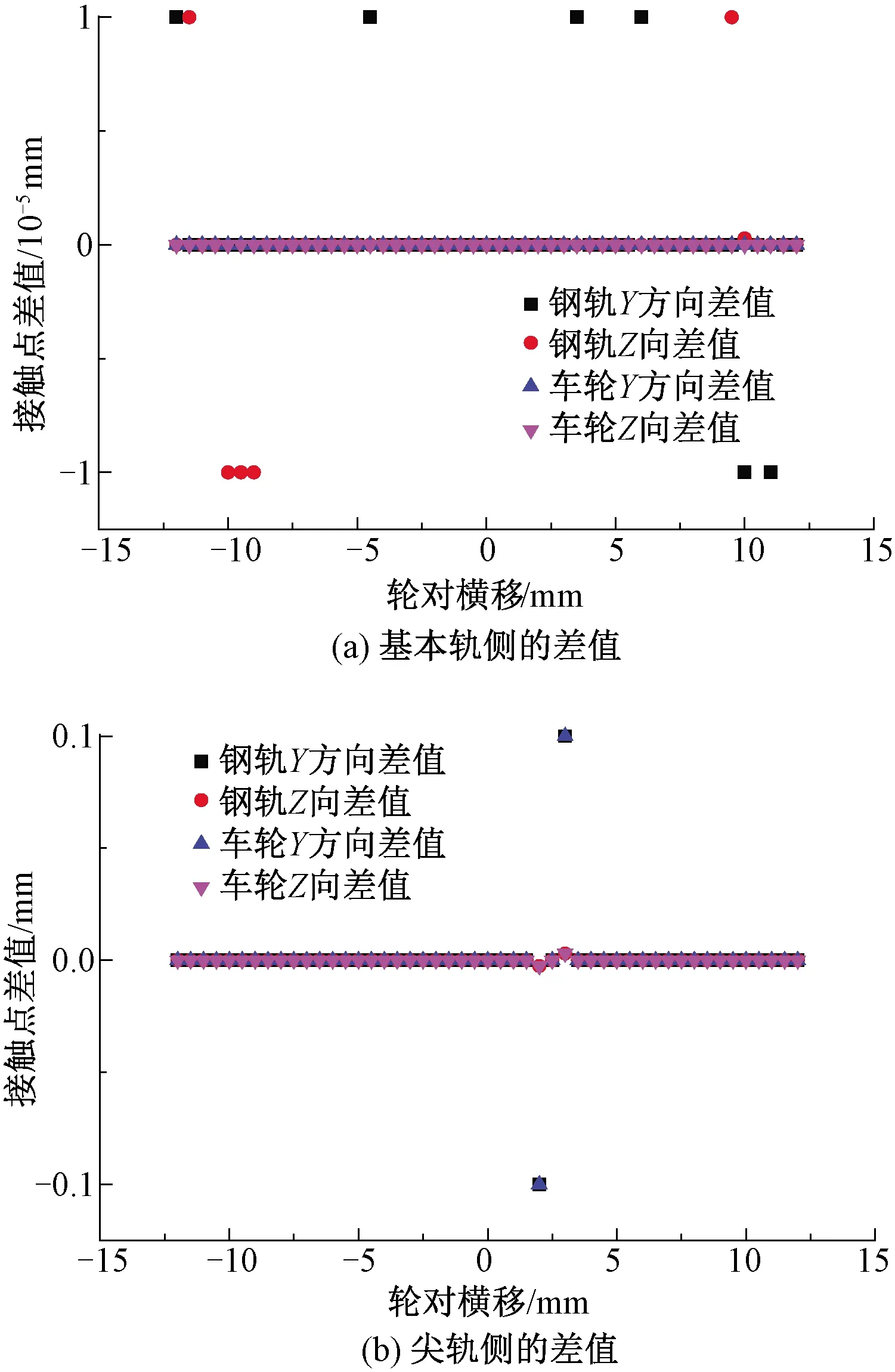
图3 两种算法的对比(轮对无摇头)

(2)法向切割法和迹线法的结果对比(轮对有摇头)

当轮对摇头角在0～0.05 rad，且选取的轮对横移量在-12～12 mm时，利用法向切割法和迹线法计算的轮轨接触点在钢轨X、Y、Z三个方向的差值如图4所示。由图4(a)、4(c)、4(e)可知，基本轨侧钢轨上由两种算法得到的轮轨接触点的在X、Y、Z轴方向上的最大差值分别为49.5、8.2、7.2 mm，并且当摇头角超过0.025 rad、轮对横移为9 mm时，在三个坐标轴方向上均出现较大差值。由图4(b)、4(d)、4(f)可知，尖轨侧钢轨上由两种算法得到的轮轨接触点的在X、Y、Z轴方向上的最大差值分别40.7、38.1、7.5 mm，且其轮对摇头角都超过0.025 rad。出现这一现象的原因在于，当轮对有摇头时，随着轮对横移的变化，轮轨接触点可能未在尖轨顶宽15 mm处，但是迹线法中假定了钢轨截面不会发生变化，这与实际不符，从而导致迹线法的计算结果不可避免地会产生误差。而法向切割法中道岔区的钢轨廓形是沿纵向变化的，并且采用移动窗的方法快速计算出道岔区轮轨接触点。

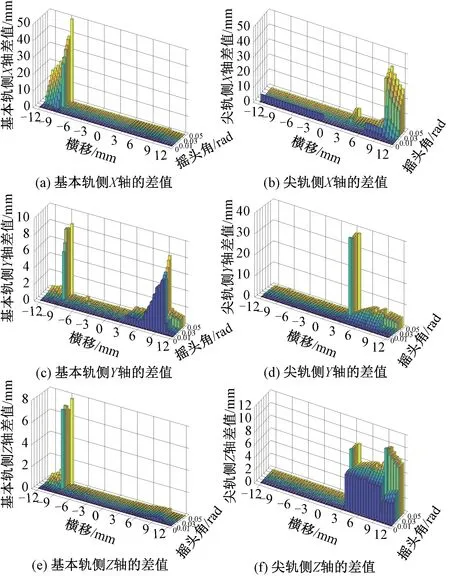
图4 两种算法对比(轮对有摇头)

综上所述，在轮对无摇头的情况下，轮轨接触点必然存在于主轮廓线对应的钢轨廓形上，三维问题可转化为二维问题，运用迹线法计算的结果是正确的。而此时通过两种算法计算结果的对比，也验证了法向切割法的正确性。在轮对有摇头的情况下，轮轨接触点不一定存在于主轮廓线对应的钢轨廓形上，此时运用迹线法会与实际有一定误差。而此时通过对比两种算法，发现迹线法的计算结果与用模拟了道岔区尖轨变截面真实情况的法向切割法计算出的结果相比存在较大差异，接触点位置差值最大能达到5 cm，而轮轨接触参数的差值比率也高达5倍，说明采用迹线法计算有摇头情况下的道岔区轮轨接触几何会与实际结果产生较大误差，说明采用法向切割法计算道岔区轮轨接触几何是有必要的。

2 车轮廓形的演变

利用Miniprof采集某条线路上不同服役时间下的高速车轮LMA型面的数据，得到车轮廓形随服役里程的演变情况，如图5所示。

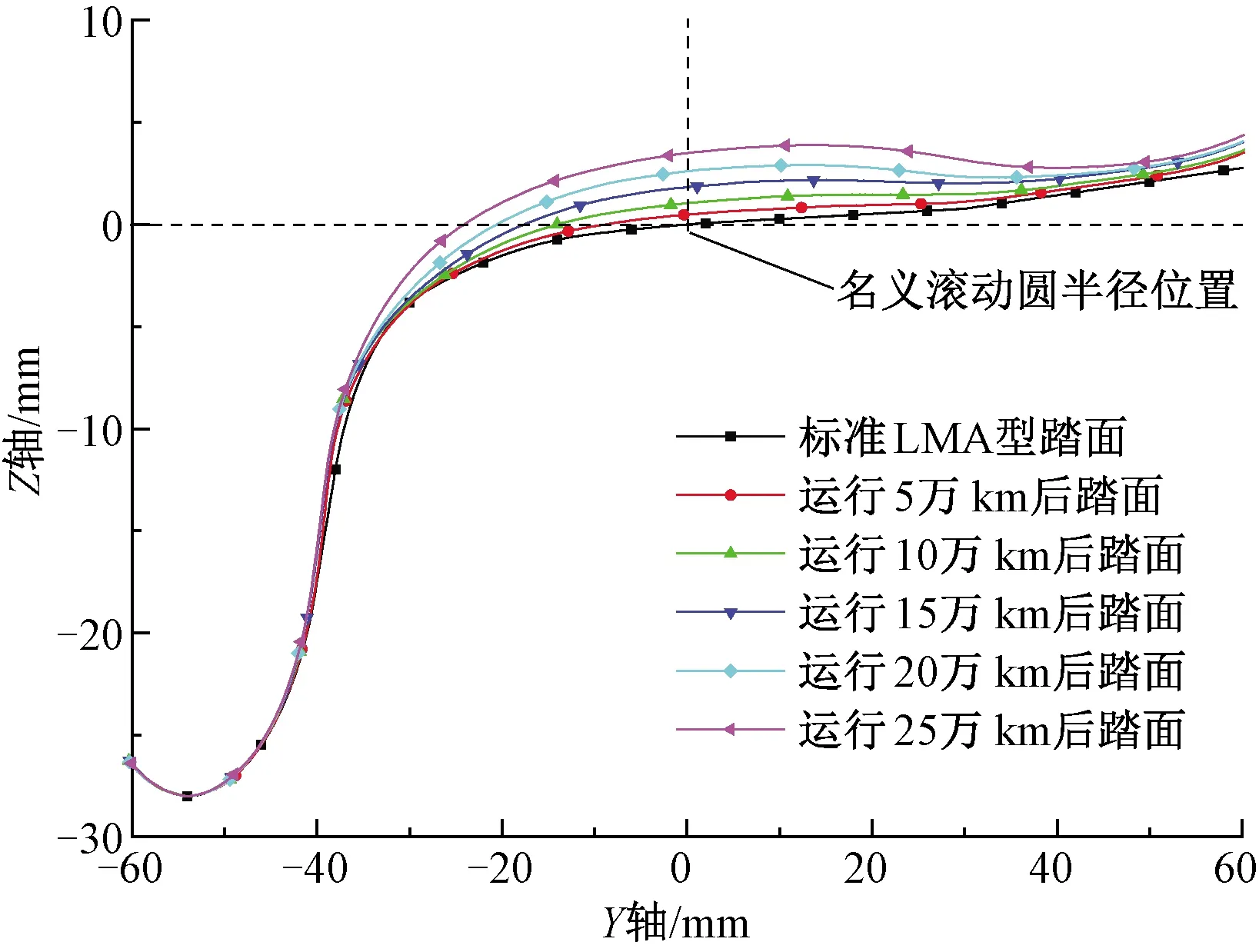
图5 实测不同运营里程下的车轮型面

由图5可知，车轮磨耗随着运行里程的增加而不断加剧，车轮廓形也会随之改变。 车轮的磨耗主要分布在踏面Y坐标-20～40 mm范围内。随着车轮型面磨耗的加深，轮轨接触发生变化，轮轨相互作用加剧，影响车轮和钢轨的服役寿命。

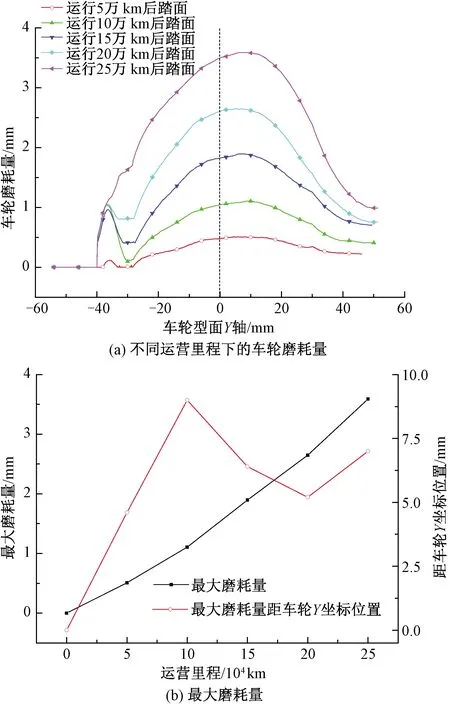
图6 车轮磨耗量

由图6可知，随着运营里程的增加，车轮磨耗量不断加深，当运营里程达到25万km后，车轮磨耗量最大值达到3.5 mm。可知，车轮最大磨耗量与运营里程的呈正比例关系，且轮轨关系随着车轮磨耗的加深而发生变化，因此车轮的发生磨耗最严重的位置是随运营里程的变化而变化的。

3 车轮廓形的演变对轮轨接触几何的影响

利用法向切割模型，计算不同服役阶段的车轮型面与速度350 km/h的18号道岔匹配时的轮轨接触点对分布规律以及滚动圆半径差、结构不平顺、侧滚角等轮轨接触几何参数，研究车轮廓形的演变对轮轨接触几何的影响。

3.1 轮轨接触点

利用法向切割法分别计算了不同服役阶段的车轮型面LMA与18号道岔区尖轨尖端、尖轨顶宽15、35、40 mm尖轨匹配时的轮轨接触点对分布规律，见图7。

如图7(a)所示，由于尖轨侧工作边与基本轨侧相同，故其轮轨接触点分布也相同。当实测标准LMA车轮(运营里程为零)与18号道岔匹配时，轮轨接触点对均匀分布于钢轨上，钢轨上的轮轨接触点会随着轮对横移量的增大从轨顶处向轨距角处发生移动。而当磨耗后的车轮LMA与18号道岔匹配时，随着轮对横移量的增大轮轨接触点从钢轨轨顶过渡到轨距角处。随着运营里程逐渐增大，车轮磨耗程度越来越严重，若轮对向左横移，则随着磨耗程度的增大轮轨接触点向轨道的非工作侧移动。

在尖轨顶宽15 mm处，其轮轨接触点随轮轨横移量的增大从基本轨过渡到尖轨，且已磨耗的车轮接触点比标准轮更早发生过渡。随着运行里程逐渐增大，车轮磨耗程度越来越严重，轮轨接触点从基本轨到尖轨上的过渡更加显著，见图7(b)。

在尖轨顶宽35 mm处，轮载过渡已全部完成。随着运行里程逐渐增大，车轮磨耗程度越来越严重，轮轨接触点向钢轨非工作边移动。运行里程为5万km和10万km时，轮轨接触点均分布在尖轨上，但随着磨耗的加深其轮轨接触点会更早过渡到轨距角处。当运行里程超过15万km后，未完成轮载过渡，且钢轨上的轮轨接触点直接过渡到轨距角附近，见图7(c)。

在尖轨顶宽40 mm处，不同服役阶段的车轮型面与其匹配时，轮轨接触点对分布规律与顶宽35 mm处一致，故不再赘述。

由此可见，由于运行里程逐渐增加导致车轮磨耗程度的增大，轮轨接触点位置会随着运营里程的增大而不断地向外侧移动，轮轨接触点的跳跃也随之加剧，极大增大了轮轨接触点的不连续性，也会对列车运行的平稳性和安全性产生不利影响。

图8为不同服役状态下的车轮与各关键断面处钢轨匹配时尖轨侧车轮上的轮轨接触点对的分布。随着运行里程的逐渐增大，轮轨磨耗程度不断增大，使得车轮上的接触点向外侧移动，轮轨接触点位置更加跳跃，影响列车的平稳性与旅客舒适度。

图8 车轮上的轮轨接触点分布

3.2 结构不平顺

结构不平顺是在不考虑轮对横移、轨道不平顺的前提下，由于道岔自身结构的原因导致接触点在横向及竖向产生变化的规律，它是引起列车与道岔振动的激振源之一。图9为18号道岔转辙器区与不同服役状态下的LMA车轮匹配时，结构不平顺随尖轨顶宽的变化情况。

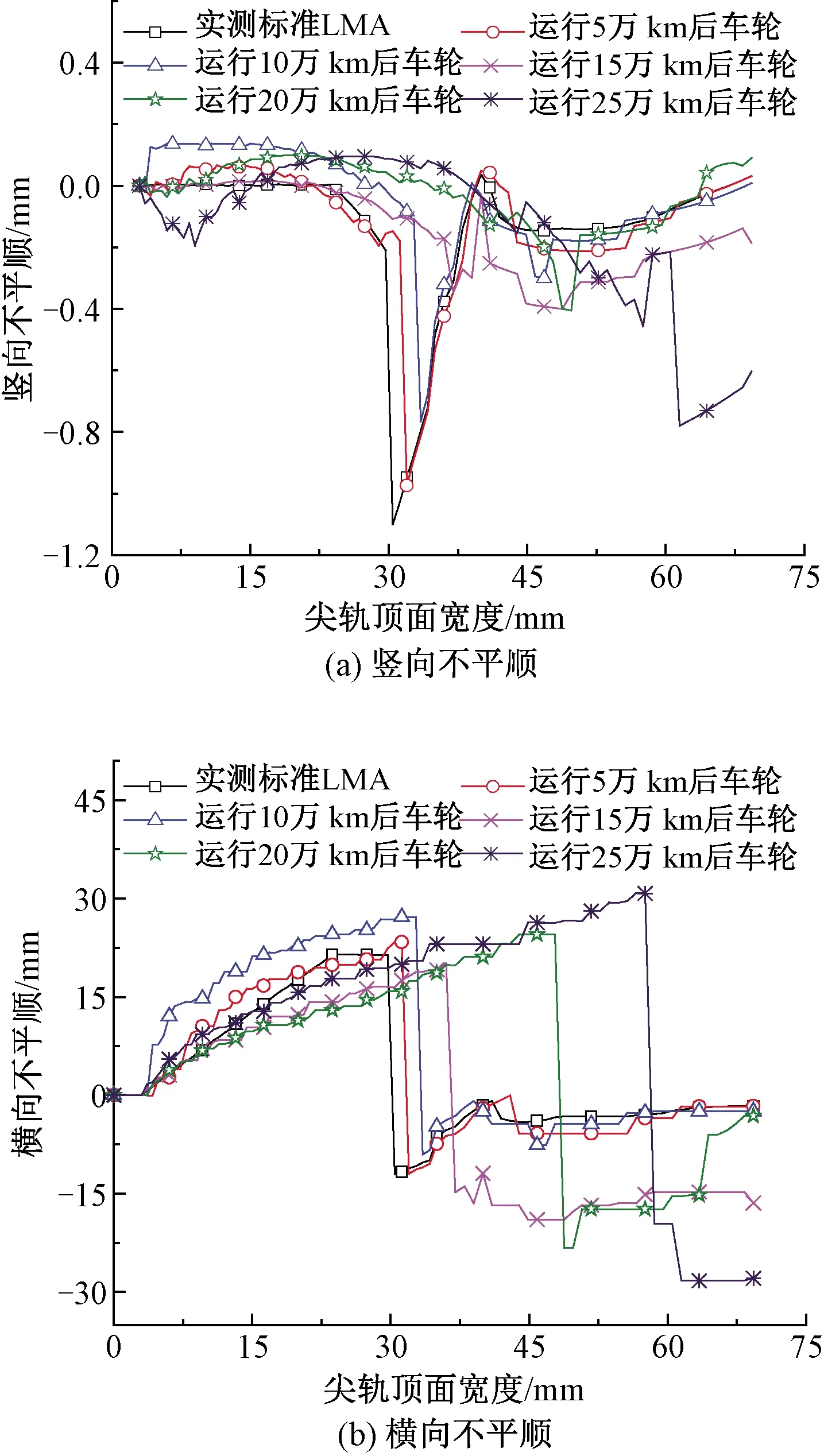
图9 转辙器部分的结构不平顺

竖向不平顺的量值较小，最大不超过1.2 mm。随着车辆运行里程的增加，竖向不平顺逐渐向上偏移，在运行10万km后尤为明显。横向不平顺由于心轨顶宽不断增大会先产生朝向线路外侧的正不平顺；当轮载过渡时，横向突变产生朝向线路内侧的负不平顺。随着车轮磨耗程度的增大，横向不平顺的量值变大，其突变的位置距尖轨尖端的距离不断增大。这是由于随着车轮磨耗的加深，轮轨接触点位置发生变化，且轮载过渡位置不断向后偏移。

3.3 滚动圆半径差随轮对横移的变化

滚动圆半径差能反映轮对的动态特性，是计算等效锥度的重要接触几何参数。但是，车辆通过曲线的能力和列车运行的稳定性对滚动圆半径差的要求是矛盾的。对列车的曲线通过性能有较高要求时，需要较大的滚动圆半径差，但这会影响车辆运行的稳定性。反之，列车运行平稳性要求较高时，需要较小的滚动圆半径差，但会影响列车过曲线的能力。

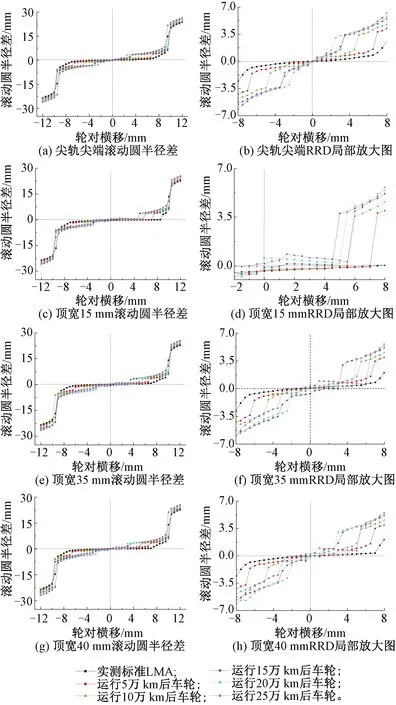
图10 关键断面处的滚动圆半径差

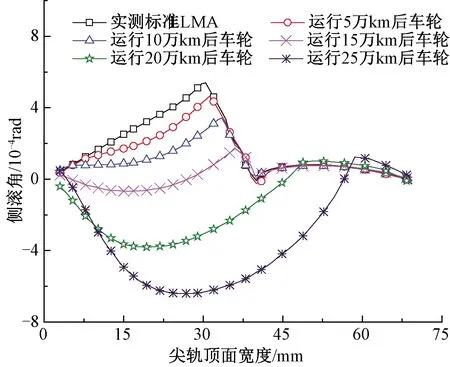
图11 侧滚角随尖轨顶宽的变化

图10所示为轮对无摇头且轮对横移量变化范围为-12～12 mm时，LMA型车轮与18号高速道岔各关键断面处钢轨匹配时的滚动圆半径差。在尖轨尖端处，由于尖轨侧和基本轨侧钢轨工作边完全相同，故在两侧随轮对横移变化的规律相同，当无横移时，滚动圆半径差为零。而在其他关键断面处，由于两侧钢轨截面的不对称，不存在滚动圆半径差和横移量均为零的情况。随着运营里程逐渐增大，车轮磨耗程度变大，滚动圆半径差为零的点不断向右侧移动，在钢轨顶宽40 mm处甚至会出现多个滚动圆半径差为零的点。这说明车轮磨耗程度的增大会加剧接触点的不连续性与随机性，导致列车运行的平稳性受到影响。

3.4 侧滚角

侧滚角可表征当轮轨发生接触时，轮对在空间中的接触姿态。在区间线路中，由于左右轮轨型面为对称截面，故当轮对无横移时，左右侧轮轨接触位置相同，轮对侧滚角为零；轮对有横移时，侧滚角随着轮对横移量的增大而增大。而在道岔区，由于钢轨变截面组合廓形特点，即使轮对无横移时，轮轨接触时轮对侧滚角也不一定为零。图11为轮对无横移时，不同运行里程后的车轮与18号道岔钢轨匹配时轮对侧滚角随尖轨顶宽的变化。随着车轮运行里程的增大，侧滚角逐渐减小，这说明车轮磨耗的加深极大地改变了轮轨接触位置，使得轮轨接触时车轮姿态发生变化。

4 结论

本文提出一种考虑道岔区钢轨变截面特点的轮轨接触几何算法——法向切割法，研究了LMA车轮与350 km/h 18号道岔转辙器区钢轨匹配时轮轨接触几何特征随列车运营里程的变化规律，结果表明：

(1) 随着车轮廓形发生演变，车轮磨耗的不断加深，轮轨接触点分布更为分散，且轮轨接触点会产生更加显著的不连续特征，使其不连续性加强，将影响列车运行的平稳性和安全性。

(2)车轮发生磨耗后，转辙器区竖向不平顺的量值较小，横向不平顺幅值明显增大，发生轮载过渡的位置不断向后偏移。结构不平顺幅值增大将导致转辙器区轮轨动态相互作用增强，加剧转辙器区钢轨的磨耗和伤损。

(3) 车轮廓形的磨耗会使得滚动圆半径差不断增大，在钢轨顶宽40 mm处甚至会出现多个滚动圆半径差为零的点，加剧了轮轨接触点的不连续性与随机性，对列车的运行平稳性有不利影响。

(4) 车轮磨耗的加深改变了轮轨接触位置，使得侧滚角逐渐减小，轮轨接触时车轮姿态发生变化。

本文仅利用法向切割法从接触几何的角度对不同磨耗程度的实测LMA车轮与350 km/h 18号高速道岔转辙器区钢轨匹配时的影响进行了详细分析，后续将从轮轨力学角度出发，研究磨耗车轮对轮轨接触力和轮轨相互动力作用的影响，为轮轨型面的镟修周期的确定提供一定的科学依据。