结合用户兴趣和改进的协同过滤推荐算法

王 岩，张 杰，许合利

(河南理工大学 计算机科学与技术学院，河南 焦作 454000)E-mail：1406397946@qq.com

1 引 言

推荐系统通过个性化的推荐算法，将不同的人和物品联系起来，挖掘出不同用户间的共同爱好，从而将个性化的物品推荐给用户，为用户购物节省了大量时间.当前，各种推荐算法以及推荐技术受到了学术界的广泛关注[1，2].日益增多的用户和商品数量为传统协同过滤推荐算法带来了各种各样的问题，如数据稀疏、冷启动和实时性低[3-5]等.这些问题使得传统推荐算法在计算用户相似性时结果不够精确，推荐效果也随之下降.因此，专家学者提出各种各样的算法对传统算法进行优化研究.韩亚楠等[6]将用户评分矩阵进行填充并结合用户兴趣对传统协同过滤算法进行改进，虽然能够有效地缓解了数据稀疏的问题，但是他的方法受限于试验环境的影响，部分情况下无法达到最优化的推荐.Zhang J等[7]提出一种利用项目域特征构建用户偏好模型的框架，然后将用户偏好模型与协同过滤相结合，同时考虑领域特征集和用户间的隐式关系，以产生更好的推荐效果.Chen Hao等[8]将平衡因子引入余弦相似度算法和皮尔逊相似度算法从而对两个算法进行优化，利用平衡因子解决不同用户间评级尺度不同的问题.郑洁等[9]将信任度引入到协同过滤算法中，结合用户偏好加权的传统相似度计算方法，计算出更加准确的相似度从而进行推荐.汪静[10]等利用用户评分和项目被用户共同评分分别计算出用户和项目的相似性，然后再分别计算出用户和项目的预测评分，最后将两者结合得出最终的预测评分.Suryakant[11]等针对基本算法中平均度量的分歧，考虑到用户的评分习惯，并将余弦相似度、Jaccard系数等三种相似度计算方法进行融合，从而来提高预测精度.

根据以上研究内容，提出了一种结合用户兴趣和改进的协同过滤算法，同时衡量用户兴趣相和项目质量属性，并将两者线性结合，求得更加精确的相似性，从而提高预测评分的精确度.

2 传统协同过滤推荐算法

传统协同过滤推荐算法依据用户的历史评分信息为用户推荐出与目标用户兴趣相似的项目[12，13].其主要流程如图1所示.

2.1 用户项目评分矩阵

传统的协同过滤算法根据得到的用户历史评分信息首先构建一个m×n阶的用户-项目评分矩阵R(m，n)，在这个矩阵中行表示有m个用户，用U表示，U={u1，u2，…，um}；列表示有n个项目，用I表示，I={I1，I2，…，In}.用户-项目评分矩阵如表1所示.

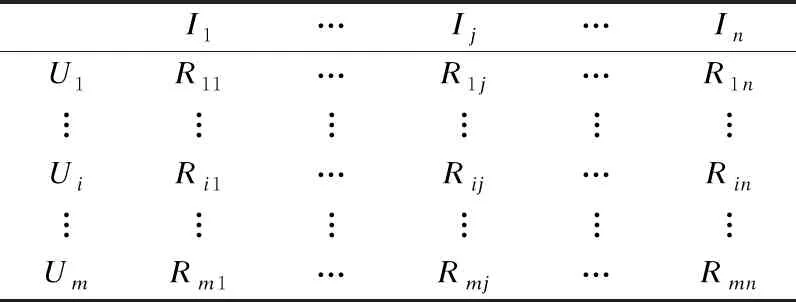
表1 用户-项目评分矩阵

2.2 推荐生成方法

传统的协同过滤算法中最广泛使用的计算相似性的方法有：Jaccard系数、Pearson相关系数和余弦相似性系数.根据以上三种方法计算出用户间的相似性，将得出的结果进行排序，选出与目标用户最接近的k个用户构成目标用户的邻居集合Y，最后使用评分预测公式得出最终的预测评分，公式如下:

(1)

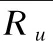
3 结合用户兴趣和改进的协同过滤算法

为了解决传统协同过滤算法在计算用户相似性时受到其他因素影响从而导致相似性计算结果不准确的问题，本文将用户评分分值差异度和用户评分倾向相似性与Jaccard系数结合计算出用户兴趣相似性，同时将Pearson相关系数加入惩罚因子进行改进，最后将用户兴趣相似性与改进的Pearson相关系数相结合计算出最终的用户相似性，从而达到提高推荐质量的目的.

3.1 用户兴趣相似性计算

Jaccard系数是一种比较常用的计算用户相似性的方法，它利用用户共同评分项目在所有项目中所占的比例来计算用户间的相似性，但它有着很明显的弊端，在计算相似性时没有考虑到用户评分对推荐效果的影响，从而导致相似性计算不准确，尤其在当前网络用户使用量非常大的情况下，这种情况最为明显 当用户.Jaccard算法公式如下：

(2)

式(2)中Iu表示用户u评分过得项目集合；Iv同理.

忽略用户评分的分值差异会影响相似性的计算结果精确度，从而影响推荐的质量.假设User1、User2、User3三个用户对项目i的评分分别为5分、4分、3分，则用户User1和User2的评分差值为1分，用户User1和User3的评分差值为2分，虽然用户User1与用户User2和User3都相似，但显然用户User1和User2的相似性更高一些.由此可以说明用户间的评分值差异直接影响到相似性计算的结果，评分差值越小，相似性计算就越精确；反之，相似性计算就越模糊.因此，本文提出分度值差异变化修正因子，计算公式如下：

(3)

式(3)中Avg(u，v)表示用户u和用户v的分值差异权重，Rui和Rvi分别表示用户u和v对项目i的评分，Cuv表示用户u和用户v共同评分的项目.由式(1)可以看出|Rui-Rvi|的值越小，Avg(u，v)就越大，用户u和v之间就越有可能有共同的爱好；|Rui-Rvi|的值越大，Avg(u，v)就越小，用户u和v之间有共同爱好的可能性就越低.

不同的用户对项目评分的观点也不相同，有的人善于表达自己的兴趣倾向，给出的项目评分就比较高.有的人对自己的兴趣有着比较严格的评判标准，给出的项目评分就比较低.因此，只是简单地使用用户间的分值差异度来衡量用户间的相似度明显不能够准确的达到高质量的推荐效果.用户评分的平均值可以用来作为衡量用户对物品评分倾向的重要因子.当用户对项目的评分大于其评分均值时，表现为正向兴趣；反之，为负向兴趣.针对这一特征，本文引入用户兴趣倾向表示用户在评分时的主观想法，计算方法为：

(4)

式(4)中SimIT(u，v)表示用户的兴趣倾向相似性.

由式(1)、(2)和(3)可以得出最终的用户兴趣相似性的计算方法：

SimI(u，v)=SimIT(u，v)×Jaccard(u，v)×Avg(u，v)

(5)

式(5)中SimI(u，v)表示用户兴趣相似性.

3.2 改进的相似性计算方法

在计算用户相似性时被经常使用的算法是Pearson相关系数.传统的Pearson相关系数公式如下：

(6)

分析式(6)可知，Pearson相关系数在计算用户相似性的前提是两个用户存在共同评分的项目集合.对于用户共同评分的项目而言，在计算相似性时认为用户对项目的所有评分都表达了用户对该项目的偏好程度，能够直接用于相似性的计算之中.相反，项目本身的质量属性也会影响用户在评分时的分值，利用这些评分计算用户相似性时，就会导致计算出的用户相似性精确度不到，推荐效果也受到相当大的影响.

项目本身的质量属性的好坏直接或间接的影响着用户对该项目的评分.这里以电影为例，假如有一部电影拍得非常难看，这与用户的兴趣偏好没有太大的关系，所以大多数的用户在评分的时候都只给了1分；相反，如果一部电影拍得非常好看，大部分用户都觉得它好看，所以在评分时可能都给了5分.那么可能任意的用户在给该电影打分时，评分可能也是1分或者5分.由此可以看出，当一个项目自身质量属性很差或者很好的时候，大部分用户就回给出相同的评分，但此时并不能说明这些用户的相似性就很高.但是，当多数用户的评分高低分布均匀时，就能很直观的反映出用户的兴趣偏好.

本文用标准差来反映用户评分对相似性计算的惩罚因子，评分标准差即离散性反映了项目自身质量属性对用户评分的影响大小.用户评分的离散程度越高，表示项目自身质量属性对用户的评分影响就越大，就越能反映用户的兴趣偏好；反之，项目自身质量属性对用户的评分影响就越小，对用户兴趣偏好的反应程度就越低.

因此，本文离散性惩罚项目自身质量属性带来的误差，将离散性引入到相似度的计算过程中，公式如下：

(7)

(8)

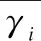
将式(8)与Pearson相关系数计算公式结合，得到式(9)如下：

(9)

3.3 结合用户兴趣和改进的协同过滤算法

针对传统协同过滤算法未考虑到用户评分差异度以及评分倾向的问题，本文在3.1节提出了一种将其全部考虑在内的计算方法(公式(5))，结合3.2节中提出的将Pearson相关系数进行改进的计算方法(公式(9))，最终形成本文所提出的新算法，其表达式为：

Sim(u，v)=λSimI(u，v)+(1-λ)SimP(u，v)

(10)

式(10)中Sim(u，v)表示最终的相似度计算方法，λ为可变参数λ∈[0，1]，用于调节用户兴趣相似度和改进的相似度的比重.

根据公式(10)计算出的相似度，得出目标用户的最近邻居集合Y，最后利用评分预测公式对目标用户进行评分预测.评分预测公式为：

(11)

根据上述方法，通过用户兴趣相似性和改进的相似性计算方法相结合，得出更加精确的评分预测结果，最后进行推荐，具体算法流程如下：

输入：用户、项目、评分数据文件，参数λ.

输出：用户预测评分值矩阵.

Step1.根据输入的数据文件构建出用户-项目评分矩阵；

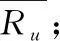
Step3.利用式(3)和式(4)计算出用户的评分差异权重和兴趣倾向相似性SimIT(u，v)，并根据式(6)计算得出用户兴趣相似性SimI(u，v)；

Step4.根据式(7)和式(8)计算用户的标准差σi和离散系数Di，并根据式(9)计算的出用户相似性SimP(u，v)；

Step5.由以上步骤得出的SimI(u，v)和SimP(u，v)，利用式(10)，输入不同的参数λ值，调整用户兴趣相似性和用户形似性的比重，得出最精确的相似性Sim(u，v)的计算结果；

Step6.根据Sim(u，v)得出的结果选出最大的k个用户形成目标用户的邻居集合Y，利用式(11)得出预测评分，形成评分预测值矩阵.

4 实验结果与分析

4.1 数据集

本文采用MovieLens和Book-Crossing两个数据集对算法进行实验验证.MovieLens数据集采用的是100k的数据文件，评分的区间在1-5分之间.数据的稀疏性可以用公式1-评分总数/用户数×项目数来计算，结果为93.7%，可见数据是非常稀疏的.Book-Crossing数据集是亚马逊用户对该平台中书籍的评分数据集，该数据集的评分范围为1-10分，从中选择2532名用户对18072本书籍的评分为本文实验数据集，在两个数据集中随机选择80%作为训练集，20%作为测试集.本文为便于记忆，将MovieLens和Book-Crossing数据集分别记为X1和X2.

4.2 评价标准

平均绝对误差(Mean Absoulte Error，MAE)：目前应用最广泛的协同过滤算法评价标准，它表示推荐值与真实值之间的平均绝对差值[14].将预测用户评分集合定义为{p1，p2，…，pn}，实际用户评分集合定义为{q1，q2，…，qn}，则MAE计算公式为:

(12)

覆盖率：覆盖率[15]能够明显的显示出推荐的物品对用户是否有效.覆盖率越大表明推荐物品概率分布越均匀，计算公式为:

(13)

其中U表示用户集合，Nu表示为用户u推荐的物品集合中物品的个数，n表示数据集中物品总个数.

召回率：召回率表示推荐物品中有多少被真实的预测到了，能够清晰的表达出推荐结果的精确度.计算公式为:

(14)

其中Ru和Tu分别表示为用户推荐的物品集合和用户真实喜欢的物品集合.

4.3 结果与分析

根据本文提出的相似性计算方法，可变参数λ在相似度计算过程中起着非常重要的作用.因此，首先需要确定λ的值来消除可变参数λ对推荐结果的影响.当最近邻用户个数为30时，MAE值在不同λ取值下的变化结果如图2所示.

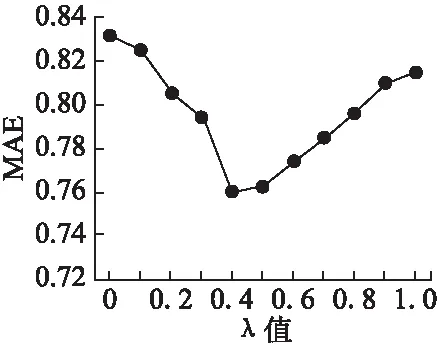
图2 算法MAE值随着λ值的变化

λ的值表示本文相似性算法中用户相似性和改进的Pearson相关系数之间的比重，当λ值较大时，说明用户相似性对本文推荐算法的影响较大，反之，说明改进的Pesrson相关系数对本文推荐算法的影响较大.由图2可知，当λ的值为0.4时，本文相似性计算方法达到最优.

将本文计算相似性方法记为UII-CF，在平均绝对误差、准确率和召回率3个方面与Pearson相似性计算方法、Jaccard相似性计算方法和文献[12]中相似度计算方法(proposed)进行比较来验证本文推荐算法的推荐效果.

图3显示了在MovieLens数据集中不同最近邻居下4种相似度算法的MAE值，从图中可以看出4种算法的MAE值随着最近邻居的不断增加而逐渐减小，并且本文算法UII-CF的MAE值小于传统的相似性计算方法，在最近邻居数为30时取得了最优值.当最近邻用户小于25时，本文算法MAE值高于文献[12]算法，但当最近邻用户大于25时本文算法优于文献[12]算法.

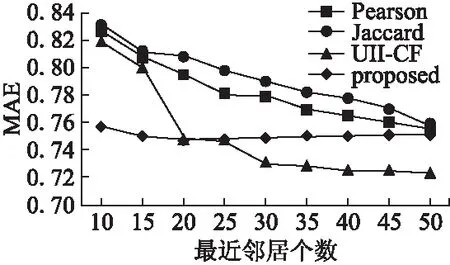
图3 X1数据集4种算法的MAE比较结果

图4给出了在Book-Crossing数据集中4种算法在不同最近邻居数下的MAE值，从图中可以看出随着最近邻居数的增加，MAE值逐渐减小，本文算法在最近邻居数达到30时取得最优值，且优于其他3种算法.由图3和图4可知本文算法在MovieLens和Book-Crossing数据集上的MAE值均优于其他3种算法.

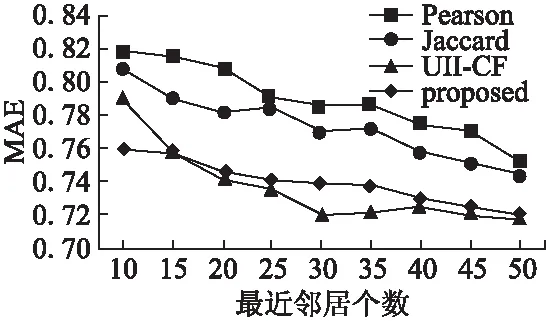
图4 X2数据集4种算法的MAE比较结果

图5显示了在MovieLens数据集中4种算法的覆盖率比较结果.从图中可以看出4种算法的覆盖率随着最近邻居数目的增大而增长，这是因为最近邻居用户的增加可能导致当做备选项推荐给用户的物品数目增加.从图5中可以看出虽然4种算法的覆盖率都在增加，但明显本文UII-CF算法覆盖率大于其他算法，因此本文所提出的算法(UII-CF)可以产生更好的推荐效果.

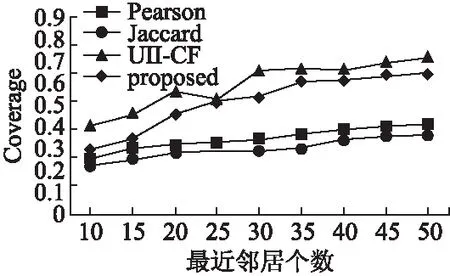
图5 X1数据集4种算法覆盖率比较结果

图6显示了在Book-Crossing数据集中4种算法的覆盖率比较结果.由图可以看出随着最近邻居的增加4中算法的覆盖率都逐渐增加，但明显可以看出本文算法的的覆盖率增加的更快.由图5和图6可知，本文算法在MovieLens和Book-Crossing数据集上的覆盖率均大于其他3种算法.

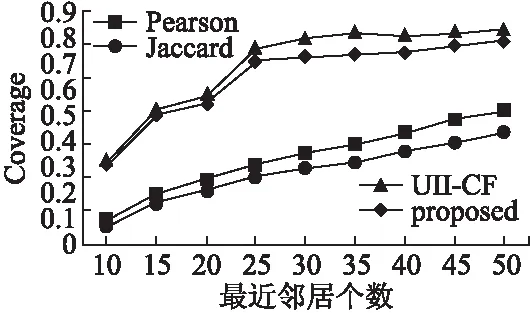
图6 X2数据集4种算法的覆盖率比较结果

图8表示Book-Crossing数据集中4种算法的召回率比较结果.从图中可以看出本文算法的召回率均高于其他3种算法.

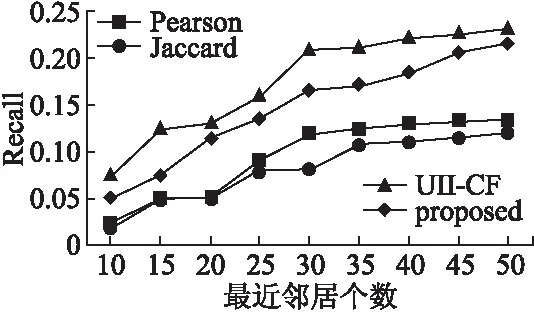
图7 X1数据集4种算法召回率比较结果

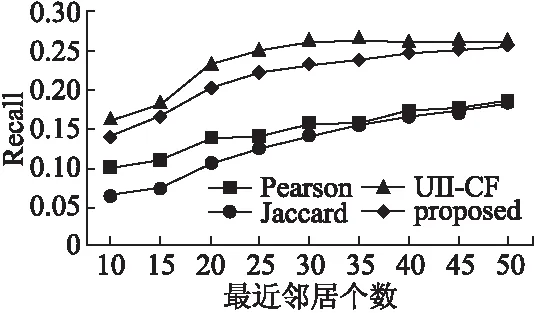
图8 X2数据集4种算法的召回率比较结果

由上述实验结果对比分析可知，本文针对用户兴趣和项目自身质量属性提出的算法(UII-CF)是有效可行的.将用户兴趣相似性与改进的协同过滤算法结合后在平均绝对误差、覆盖率和召回率方面都要优于传统的协同过滤算法，经过实验验证表明本文算法能够在提高推荐精确度方面有着很好的效果.

5 结束语

本文针对传统协同过滤算法面对稀疏数据计算相似度不准确，导致推荐效果不佳的问题，通过对用户兴趣的分析，提出用户兴趣相似度的计算方法，同时将惩罚因子加入到Pearson相关系数的计算方法中用以消除项目质量属性对相似性计算带来的误差.最后将两者结合后得到本文算法(UII-CF)计算出更加精确的相似性.实验表明，该方法能够有效降低平均绝对误差，提高覆盖率和召回率，提高推荐质量.在现实生活中用户的兴趣会随着时间的迁移而变化，导致推荐结果会受到一定的影响，以后需要针对用户兴趣变化问题做进一步研究，从而提高推荐质量.