1960—2016年辽河流域极端降水时间序列变化

刘海金

（东华理工大学，江西 南昌 330013）

日前，全球气候变化已引起政府、非政府组织及学者们的广泛关注[1-6]。在气候变化的背景下，极端气候事件对经济发展的影响越来越明显，甚至对人体健康产生了重大不良的影响[7]。同时，全球气候变化引起河流流域内洪涝灾害多发，而极端降水又是影响极端洪涝的重要水文因素[8]，因此，如何对极端降水事件有效地预测已成为实现流域内可持续发展的必经之路。

目前对流域内极端降水事件的研究取得了大量成果，其中长江、黄河、珠江等河流是主要的研究对象[9-19]，同时也有研究成果是以中国多流域为空间尺度[20-21]，另外对于辽河流域的具体研究多集中于辽河的分区概况[22-24]及少量台站的全流域研究[25]，对其全流域多台站的研究相对较少。本研究以1960—2016年辽河流域及其周边的气象台站数据为依据，利用计量方法对日降水强度、日降水大于20 mm的日数、年内一日最大降水总量等多个指标进行诊断，得到辽河流域56年极端降水的时空变化，并预测未来发展趋势，以期为辽河流域经济社会的发展与防灾减灾工程的建设提供降水参考依据。

1 研究区概况及数据来源

辽河流域地处中国东北地区的南部（116°54′~125°32′E，40°30′~45°17′N），是东北地区最重要的河流之一，也是中国的七大流域之一。辽河发源于光头山，流经冀、蒙、吉、辽4省，共经16个市（地、州），56个县（县级市、县、旗），最终汇入渤海。辽河流域总面积为219 631 km2，全长1 345 km，由西辽河、东辽河、太子河、浑河等支流组成，上游支流稀疏细长，中下游支流密集短小。

本研究日降水及相关数据均来源于中国气象数据网（http://data.cma.cn/）。基于辽河流域范围及数据的有效连续性，选取37个气象台站的数据进行分析（图1）。对微量数据作归零处理，对极少的缺测数据进行剔除，以确保数据的完整性。

2 研究方法

本研究所选取的极端降水指数均来自于世界气象组织气候委员会（WMO） 等推荐的11个极端气候指数（表1）。利用一元线性趋势分析对各极端分析，以确定各极端降水指数的总体变化趋势。利用Mann-Kendall突变分析对各极端降水指数进行突变检验，以确定各极端降水指数的突变年份。建立评价体系，利用因子分析对辽河流域极端降水进行总体评价，以确定辽河流域降水极端性的综合变化趋势。利用R/S分析对因子分析评价结果进行变化趋势的分析，以确定辽河流域降水极端性变化趋势的显著性特征。

2.1 一元线性趋势分析

一元线性趋势分析可确定要素的平均变化趋势，具体公式为：

式中：y——气候要素序列（降水要素）；x——时间序列（1960—2016年）；b——线性趋势系数，其正负反映上升或下降趋势；b——气候要素每10 a的气候倾向率[26]；a——截距。

2.2 M-K突变检验

气候突变的普遍式定义为：气候从一种稳定态（或稳定持续的变化趋势）跳跃式地转变到另一种稳定态（或稳定持续的变化趋势）的现象，它表现为气候在时空上从一个统计特性到另一个统计特性的急剧变化[27]。M-K突变检验是一种非参数类的统计检验方法，其基本原理为：

2.2.1 构建秩序列

设气候要素x在时间序列上有n个样本，可构建秩序列：

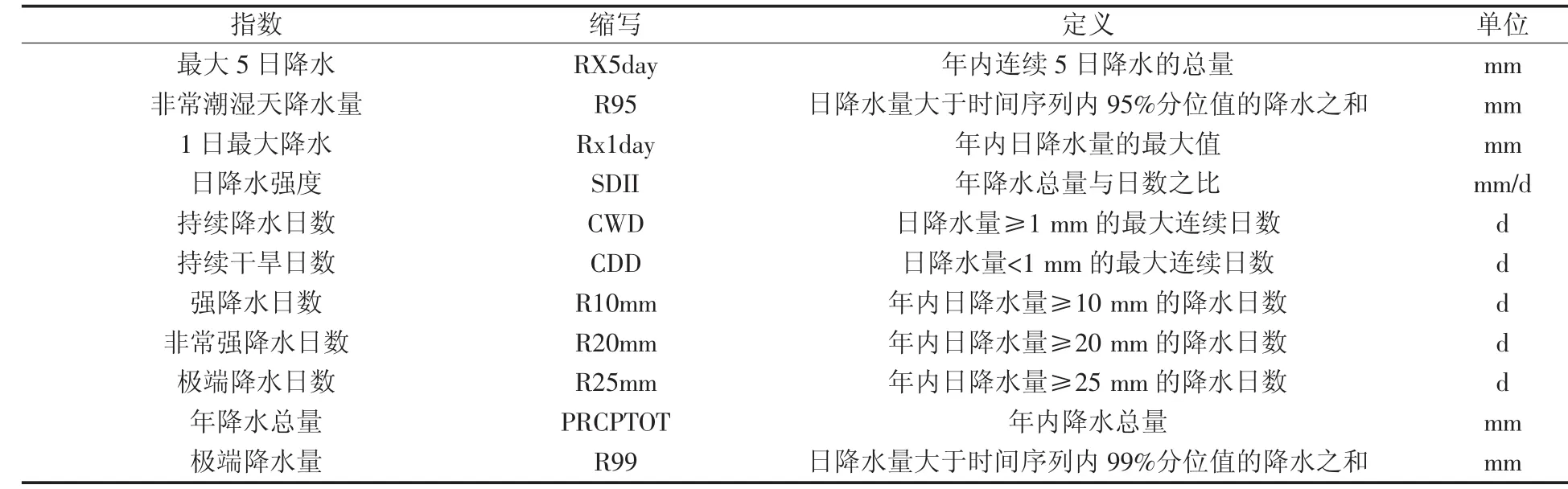
表1 极端降水指数的定义

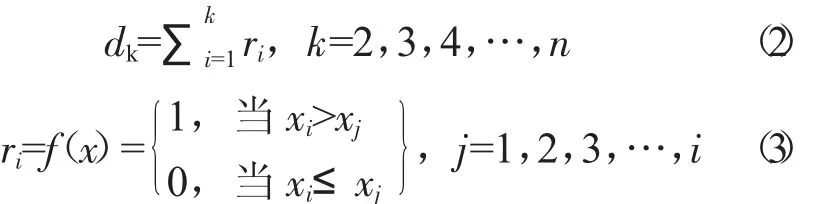
式（2）中：dk——序列内x的第i个数值大于第j个数值的数量统计量。

2.2.2 dk的标准化处理

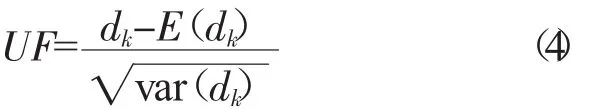
式中：E（dk）——秩序列的dk均值；var（dk）——方差。

按照逆序列重复上述过程，得到UBK=-|UFK|，且UB1=0。若UFK＞0，则说明该序列上升，反之下降；当超过置信水平时，说明变化趋势显著。如果UFK与UBK相交且交点在置信区间内，则交点表示的时间即为突变发生的时间。

2.3 因子分析

处理数据时，利用数学方法将多个性质相同的变量组合为一个变量，称为因子，即用较少的综合指标来代替多指标。因子分析就是基于因子结合的分析方法，如果数据选取合理，因子分析不仅损失的原始数据较少，且能够提取影响数据的主要因素，反映事物的本质现象[28]。其基本步骤为：利用KMO和Bartlett法检验数据是否适合因子分析，若K-B的球形度检验＞0.5且Bartlett的检验为0，即可进行因子分析[29]。然后建立相关系数矩阵，计算其特征值与相关系数矩阵，根据特征值大于1或者贡献度为80%来确定主成分因子，得到得分系数矩阵，并根据权重计算最终得分。此数据的计算均在IBM SPSS Statistics 21中进行。

营养水平参照NY/T 816-2004配制育肥山羊日粮，配方（D）组成见表1。人工配料，混合机混合均匀，KL-150型颗粒机（压缩比6∶1）制粒。

2.4 R/S分析

R/S分析是英国学者Hurst在1965年提出的关于处理时间序列的一种分析方法[30]。研究发现，R/S降水的时间序列上具有Hurst效应，适合应用此方法[31]。Hurst指数（0＜H＜1） 在不同的取值范围具有不同的指示意义：当H=0.5时，说明各个指标之间无关联性，要素在时间序列上具有随机性，变化趋势不显著；当H＞0.5时，表明要素在未来时间序列上与历史时间序列相同，且H越接近于1，变化特征越显著；当H＜0.5时，表明要素在未来时间序列上与历史时间序列相反，且H越接近于0，变化特征越显著。

3 结果分析

3.1 极端降水指标的趋势分析

为得到辽河流域的极端降水指标的变化趋势，利用一元线性趋势分析方法对辽河流域的极端降水指标进行分析及预测，结果如表2和图2所示。在1960—2016年间，辽河流域的极端降水指数中，除日降水强度上升明显，气候倾向率大于0外，其他极端降水指数均呈下降趋势，其中强降水日数、极端降水日数及持续降水日数下降趋势明显，气候倾向率分别为-0.2 d/（10 a）、-0.109 d/（10 a）、-0.256 d/（10 a），而其他指标虽有下降但趋势并不明显。且在2010—2016年间，除持续降水日数稍有下降，其他极端降水指标均有所上升。对于极值，除持续降水日数的极值外，其他10个极端降水的指标基本都出现在1996—2016年，说明1996—2016年辽河流域的极端降水指标存在明显的不稳定性。综合说明，辽河流域在1960—2016年间降水极端性的变化呈总体下降趋势，且在56年间呈现上升趋势，在1996—2016年内波动趋势明显。

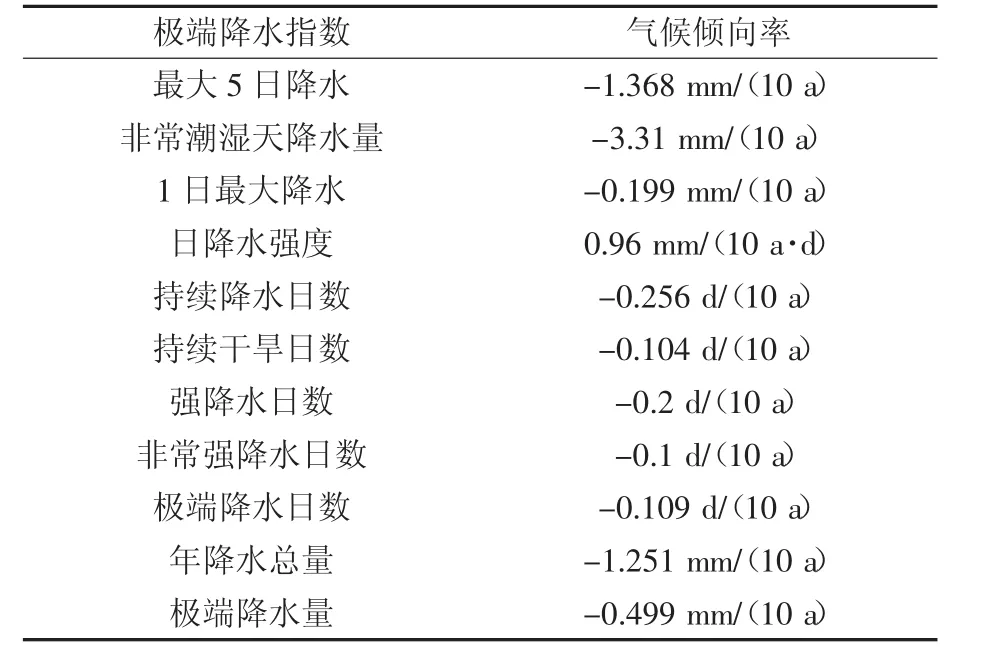
表2 辽河流域各极端降水指数气候倾向率

3.2 极端降水指标的突变分析

通过M-K突变检验可进一步确定极端降水指标的变化趋势。其中，正序列的数据统计曲线标识为UF，逆序列的数据统计曲线标识为UB。

由图3可知，日降水强度UF曲线与UB曲线相交于1983年与2001年，说明日降水强度的突变年为1983年和2001年。非常强降雨日数的UF曲线与UB曲线存在多个交叉点，说明其突变年份不明显。一日最大降水UF曲线与UB曲线相交于7个交点，说明突变年份不明显。持续降水日数的突变年份为1970年；年降水总量的突变年份为1964年；非常潮湿天降水量的UF曲线与UB曲线交点较多，说明非常潮湿天降水量不存在明显的突变年份。持续干旱日数UF曲线与UB曲线共相交于9个交点，说明持续干旱日数的突变年份不明显；强降水日数在1965年发生突变；极端降水日数发生突变的年份为1965年。最大5日降水UF与UB曲线相交于1964年、1993年、1994年，且均位于置信区间内，说明最大5日降水出现突变的年份为1964年、1993年和1994年；极端降水量发生突变的年份为1990年、1992年、1994年和2009年。

综合上述特征可以判断：辽河流域的极端降水指标的突变年份存在明显的不同：最大5日降水、极端降水量、日降水强度存在着多个明显突变年份；强降水日数、极端降水日数、持续降水日数、非常强降水日数、年降水总量存在着1个明确的突变年份；非常潮湿天降水量、持续干旱日数不存在明显突变年份。

3.3 辽河流域极端降水的适应性评价

为对辽河流域1960—2016年间极端降水进行综合评价，通过因子分析利用极端降水指标建立评价体系，结果如表3所示，得到时间序列内辽河流域极端降水的综合得分变化，并利用R/S分析对综合得分的变化趋势进行判断。

通过IBM SPSS Statistics 21软件，对辽河流域的极端降水指标进行自动标准化并保存为变量，消除指标之间的差异影响。在标准化数据的基础上，利用KMO和Bartlett法检验数据是否适合因子分析，经计算此类数据的KMO检验为0.89，适合作因子分析。然后，计算其特征值与相关系数矩阵，并以特征值大于1为标准，提取3个因子并计算最终综合得分。

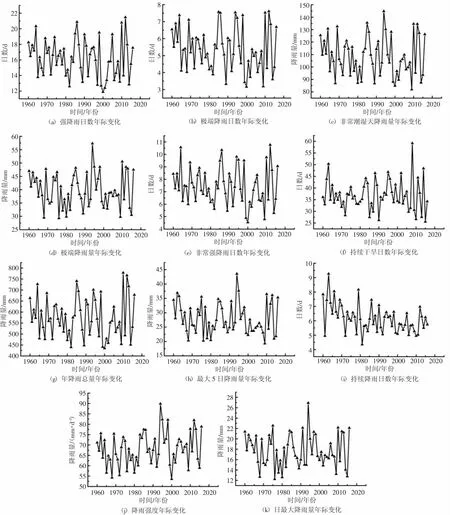
图2 辽河流域1960—2016年极端降水指标变化趋势

4 辽河流域极端降水与ENSO现象的关系

ENSO是发生在太平洋及印度洋之间的特殊气压振动，与我国的降水存在一定的联系[34]，但在不同地区ENSO对其影响不同[35]。将辽河流域极端降水综合得分与厄尔尼诺、拉尼娜强度进行比较，结果如图5所示：辽河流域的极端降水与厄尔尼诺的强度基本呈现正相关关系，厄尔尼诺强度大的年份，辽河流域降水的极端性也会呈现附近时间的峰值；辽河流域的极端降水与拉尼娜强度大致呈负相关，当拉尼娜强度增加时，辽河流域降水的极端性随之增大，当拉尼娜强度减小时，辽河流域降水的极端性也会随之减小。对于形成此现象的具体原因还需进一步进行探讨。

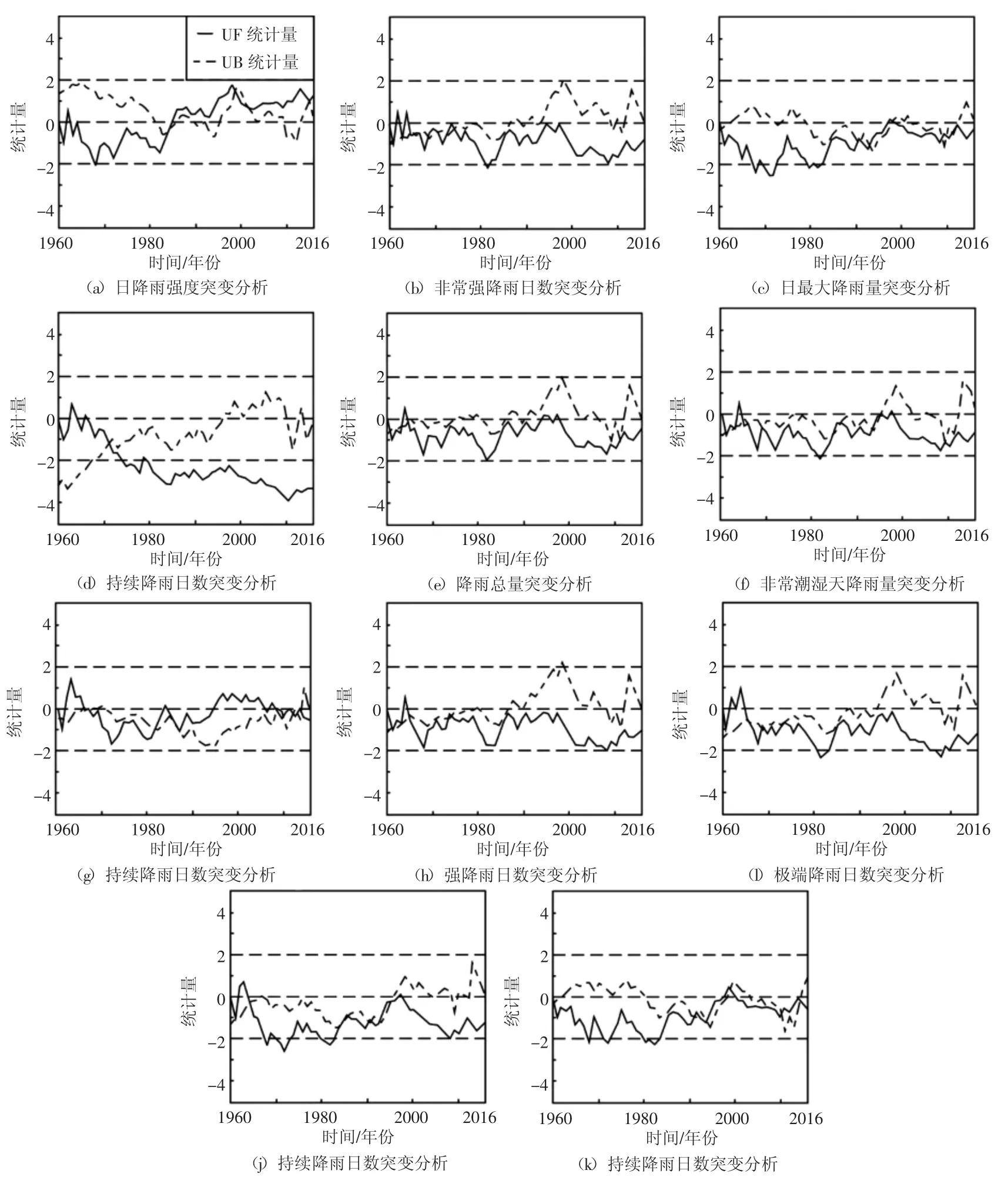
图3 辽河流域各极端降水指标突变分析

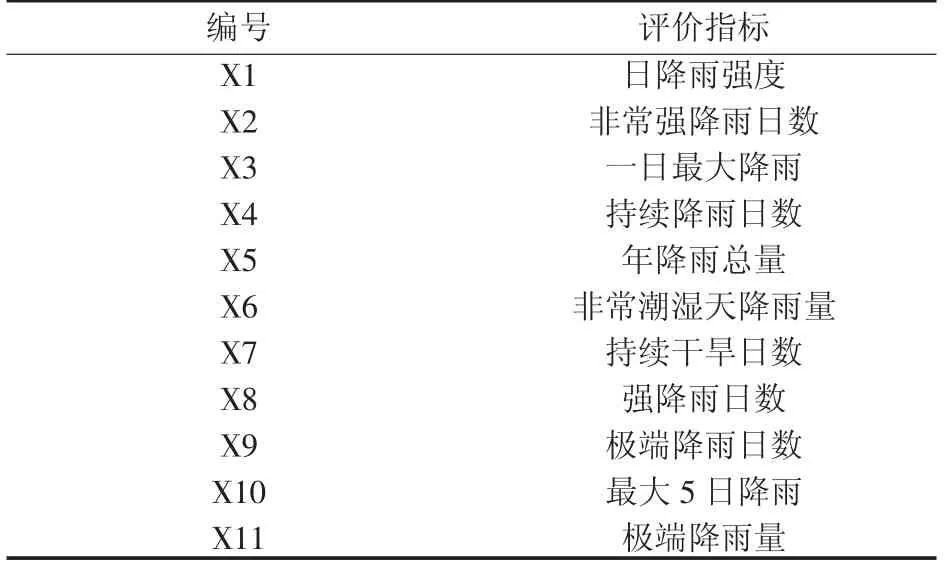
表3 辽河流域极端降水评价体系

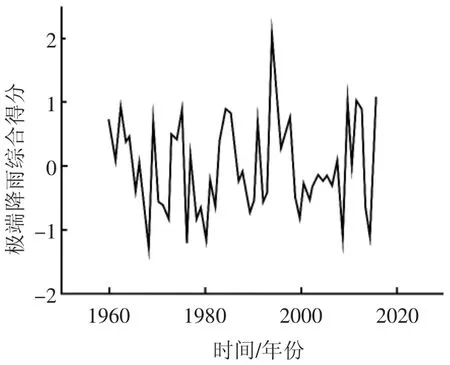
图4 辽河流域极端降水综合得分

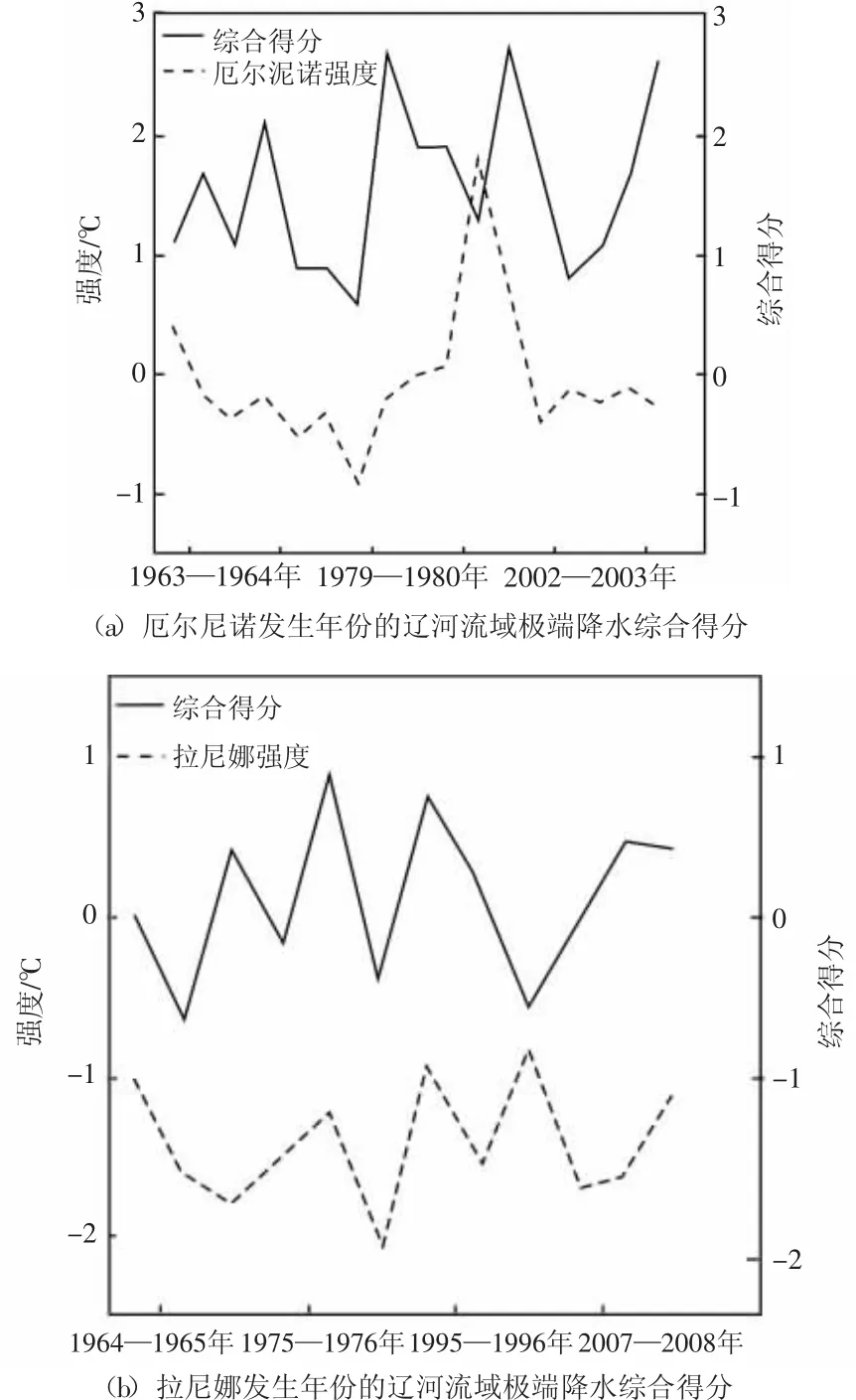
图5 辽河流域降水极端性综合得分与ENSO强度关系

5 结论

利用多种计量方法，对辽河流域的极端降水指标进行较为全面的分析，得到以下结论：

（1） 辽河流域在1960—2016年间降水极端性的各个指标的趋势、突变、周期变化存在差异，绝大部分处于下降趋势。其中，日降水强度呈上升趋势，非常强降水日数呈下降趋势，一日最大降水呈下降趋势，连续降水日数呈下降趋势，年内降水总量呈下降趋势，非常潮湿天降水量呈下降趋势，持续干旱日数基本保持不变；强降水日数呈下降趋势，极端降水日数呈下降趋势，最大5日降水和极端降水量均为下降趋势。

（2）辽河流域的极端降水指标的突变年份与周期存在明显的不同。最大5日降水、极端降水量、日降水强度存在着多个明显突变年份；强降水日数、极端降水日数、持续降水日数、非常强降水日数、年降水总量存在着1个明确的突变年份；非常潮湿天降水量、持续干旱日数不存在明显突变年份。

（3）辽河流域极端降水的综合得分在未来的变化趋势不显著，并与ENSO存在一定关系。通过计算得到综合得分线性趋势系数为0.001 2，Hurst=0.595 982 768，说明仅仅存在不显著的小幅上升。且通过对比相关年份综合得分与厄尔尼诺/拉尼娜强度，发现其与厄尔尼诺呈正向关系，与拉尼娜强度存在负向关系。