海杂波中基于可控虚警K近邻的海面小目标检测

郭子薰 水鹏朗 白晓惠 许述文 李东宸

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(中国船舶工业系统工程研究院 北京 100094)

1 引言

对于海面警戒雷达来说，在小擦地角下提高海面小目标的检测能力是一项长期且困难的工作，这类小目标主要指浮冰、小船、蛙人和飞机残骸等[1]。大致原因如下：第1，小目标具有很小的雷达截面积(Radar Cross Section, RCS)和较弱的雷达回波；第2，海杂波具有复杂且变化的特性，例如较宽的多普勒带宽和较强的非高斯特性等[2]。为了检测小目标，通常采取两种方式：高分辨率和长观测时间，其中前者可以降低杂波功率水平，后者可以增加目标回波的累积增益。但是在传统雷达中，会面临一个波位上长驻留时间和扫描效率上的矛盾。随着雷达系统的不断发展，2003年麻省理工(Massachusetts Institute of Technology, MIT)的林肯实验室[3,4]提出了泛探雷达(ubiquitous radars)，其同时利用多个接收波束覆盖整个观测空域实现了在所有方向下的全时观测。所以，在长观测时间下提出一种有效的检测小目标的方法是有必要的。但是，由于海杂波的长时非平稳特性和目标回波复杂的幅度和多普勒调制，海杂波和目标回波都很难被建模为简单有效的参数模型[5]。随着对海杂波和小目标回波的深入研究，研究者提出了时频分析、分形特性和机器学习等方法[6—8]来解决这一类问题。总的来说，都是通过研究海杂波和目标回波在各个域上的不同特性来对二者进行区分。

在1993年，Haykin等人通过对海杂波时间序列的分形(fractal)特性进行研究，进一步发现分形维数可以被用作特征以帮助实现目标检测。为了使用更多的特征来提高检测性能，Shui等人[9]进一步提取了1个幅度特征和2个多普勒特征，并将3个特征联合起来建立特征空间中的三维凸包以实现最终检测。通过IPIX雷达数据集[10]的验证，基于3特征的检测器与基于单特征的检测器相比，实现了更优的检测性能。这可以归功于多个来自不同域互补的有效特征的联合使用。但是，目标回波有时会落入多普勒域的主杂波带内，这大大影响了检测结果。为了解决这一问题，另一种基于时频3特征的检测器被Shui等人[11]提出，大大改善了检测器的性能。但是，通过对检测结果的研究发现，两个基于3特征的检测器分别在不同的数据上表现优异。考虑到不同特征对不同数据的敏感性，联合使用更多的互补特征来设计高维空间中的检测器就成为了进一步提高检测性能的有效途径。

在机器学习领域中，有很多分类能力优异的算法，比如支撑矢量机(Support Vector Machine,SVM)、神经网络(Neural Network, NN)等。我们尝试将雷达目标检测问题与机器学习算法结合起来，设计在高维特征空间中的检测器。在本文中，为了获得更好和更具有鲁棒性的检测结果，已有的来自不同域的7个有效特征被联合使用，包括归一化Hurst指数(Normalized Hurst Exponent,NHE)[12,13]、相对平均幅度(Relative Average Amplitude, RAA)、相对多普勒峰高(Relative Doppler Peak Height, RDPH)、相对向量熵(Relative Vector Entropy, RVE)[9]、脊累积(Ridge Integration,RI)、连通区域数目(Number of connected Regions,NR)和最大连通区域尺寸(Maximal Size of connected regions, MS)[11]。由于该多个特征使得杂波与目标都处于七维特征空间，从而一些已有的方法在高维(n＞3)空间中计算复杂度极高或者不再适用。例如，由于已有的基于3特征的检测器[9,11]使用凸包来决定最终的判决区域，相继通过收缩凸包实现虚警控制。但是，凸包只能在小于等于三维的空间中使用，一旦到四维或更高维，凸包的计算代价将会非常大，甚至无法计算，所以这就是其不能推广到高维的原因。后来，本团队为了突破维数限制的问题，提出了基于特征压缩的检测器[14,15]，可以将原本在高维空间中的特征压缩至三维空间。与以往基于单特征或3特征的检测器相比，基于特征压缩的检测器获得了更加优异的性能。但是在特征压缩的过程中，压缩损失是不可避免的。本文不仅为了利用更多的已知特征使得对目标有更好的检测，同时也为了避免压缩来带的性能损失，使用了机器学习中的K近邻(K Nearest Neighbours, K-NN)算法。但是由于K-NN无法实现对虚警率的有效控制，所以本文提出了一种基于可控虚警的改进K-NN方法，有效地解决了问题。

本文的工作安排大致如下：第2部分先回顾所使用的特征，并介绍一种典型的仿真目标回波产生器；第3部分提出了基于可控虚警的改进K-NN检测方法；第4部分利用实测数据对所提出的检测器进行性能评估，并与其它基于特征的检测器进行对比和分析；最后，第5部分会对本文的工作进行总结评价。

2 仿真目标回波产生器及7特征概述

雷达目标检测问题可以归结为以下2元假设检验问题[5,9,11,13—15]

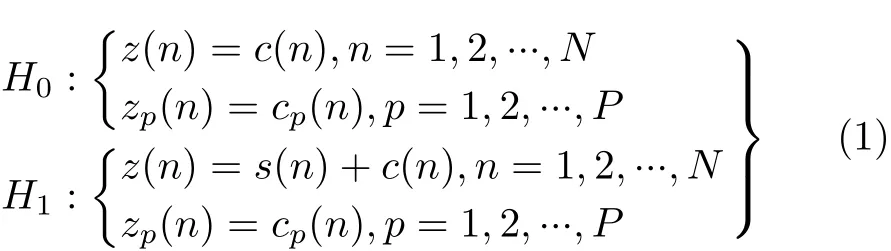
其中，z(n)和zp(n)分别表示待检测单元和周围参考单元所接收的复时间序列，c(n)和cp(n)分别表示待检测单元和周围参考单元的纯杂波时间序列，s(n)表示目标回波时间序列，P为参考单元数目，N为脉冲长度。在零假设H0下，待检测单元所接收的时间序列为纯杂波，其具有与周围参考单元的杂波序列相同的统计特性和多普勒特性。在备择假设H1下，待检测单元所接收的时间序列为带有目标的回波时间序列。

2.1 7种有效特征概述

在检测器的设计中，7种有效特征被使用，包括两个幅度特征：NHE, RAA[9,12,13]，两个多普勒特征：RDPH, RVE[9], 3个时频特征：RI, NR,MS[11]。对于两个幅度特征，若雷达回波数据包含目标，则其NHE和RAA的取值均大于纯杂波。此外，我们对回波数据的多普勒幅度谱进行分析并提取有效特征RDPH和RVE，当发现待检测单元包含目标时，RDPH较大，RVE较小；当待检测单元为纯杂波时，RDPH较小，RVE较大。但是，目标回波容易落在多普勒域的主杂波带内，使得前4种特征不再适用，那么3个时频特征就可以在这种情况发挥作用帮助完成目标检测。当雷达回波包含目标时，RI和MS取值较大、NR取值较小；反之，当回波是纯杂波时，RI和MS取值较小、NR取值较大。

通过提取7个有效的海杂波和目标的特征，目标检测问题就可以近似地被转化为一个在七维特征空间的二分类问题。由于不同的特征对不同的数据或者海态都有不同的敏感性，那么基于单个特征的检测器就不会对任何情况都适用和有效。对目标检测问题来说，联合使用7个有效特征来构建高维特征空间中的检测器无疑是一种综合有效的方法。

2.2 仿真目标回波产生器

由于海面小目标的多样性和目标与海表面之间复杂的相互运动，获取所有种类的目标的有效信息是不可能的。考虑到雷达的工作模式，大量的杂波数据可以被快速地收集，相比之下，只有少量的目标数据被获取，这就导致了两类样本数量的不均衡。在我们的工作中，使用已有的杂波信息对典型目标回波进行仿真以辅助完成后续检测器的设计。具有匀速和匀加速运动状态的典型小目标回波可以被表示为[15]

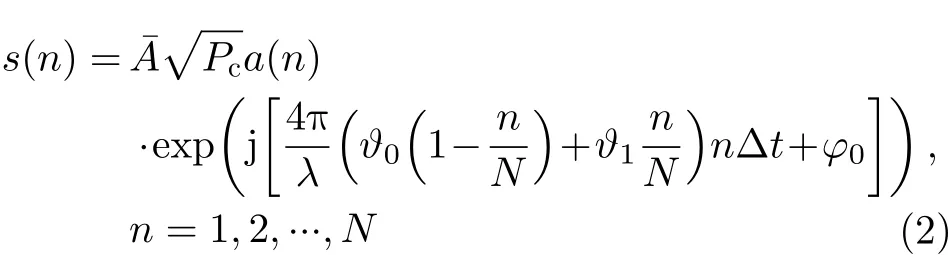
通过对公开IPIX数据集的研究发现，当信杂比低于—10 dB时，目标无法被检测到；当信杂比高于20 dB时，目标一定可以被检测到，所以将经验参数 A¯设置为[—10 dB, 20 dB]的对应区间[10—1,101/2]上的均匀分布，用于调节信杂比，Pc是杂波的平均功率，a(n)是一个高度相关的取值为非负的随机序列，被用于模拟小目标的幅度波动， λ是雷达的工作波长， ϑ0和 ϑ1分别是目标的初始和终止径向速度， Δt是 雷达的脉冲重复周期， φ0是随机分布于区间[0, 2π]上的初始相位，N是仿真目标回波信号的长度。

考虑到小目标幅度的物理特性，幅度序列a(n)被建模为一个非负的、高度相关的、单位功率的随机序列，并具有可调动态范围和去相关时间。序列a(n)的生成步骤分为如下4步：第1，生成一个独立、同服从在区间[0, 1]上均匀分布的序列u(n)；第2，由于幅度序列具有高度的空时相关性，所以将随机序列u(n)作为一个1阶自回归模型的输入[15]

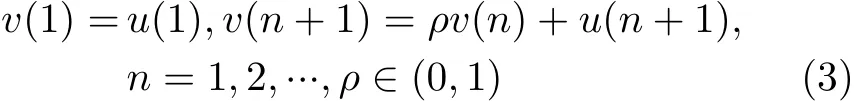
即可产生高度相关的序列v(n)，其中 ρ ∈[0.95,0.99]表示1阶相关系数，经计算，此处序列v(n)的取值范围在区间[—1/(1 -ρ ) , 1/(1 -ρ)]内；第3，由于目标的幅度为非负值，所以将序列v(n)转化为一个非负的序列v+(n)

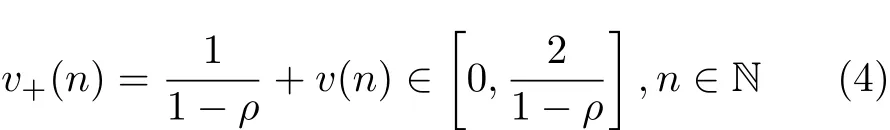
第4，由于刚开始产生的幅度序列不够稳定，所以为了避免这种情况我们只选取后续产生的幅度序列v+(n+M)，其中M是一个足够大的正数，再对序列进行功率归一化，即可得到最终的幅度序列a(n)

其中，E{v+2}是序列v+(n)的功率。

此外，初始径向速度 ϑ0和 终止径向速度 ϑ1可以被表示为[15]

其中，θ为雷达视线与目标运动方向的夹角，服从[—π, π]上的均匀分布，v0和v1分别表示目标的初始速度和终止速度，随机数x,y,z是相互独立的。值得注意的是，当加速度的限制条件不满足时，随机数x和y需要重新产生。在目标回波仿真过程中，η的经验取值为5 m/s, ζ的经验取值为2 m/s2，其对应于小目标的速度在[—5 m/s, 5 m/s]之间，不超过10节，最大加速度为2 m/s2。通过上述步骤，一个典型的仿真目标回波产生器被构建。需要注意的是，该仿真目标回波产生器旨在生成足量的不完备的目标回波样本，为后续检测器的设计提供更多有效信息，而不是覆盖各种各样的目标回波。

图1是在HV极化下第1组数据的真实目标回波和仿真目标回波的7个特征的对比图，其中真实目标特征用蓝色表示，仿真目标回波用红色表示。由此可知仿真目标回波产生器的有效性，进一步仿真目标回波的特征与真实目标回波的特征也是十分接近的。

3 基于可控虚警的改进K-NN方法

很多机器学习算法可以有效地解决分类问题，比如SVM, K-NN, NN等。但是普通的二分类问题和目标检测问题存在着两点不同：第一，在普通的二分类问题中，两类样本的数量是均衡的，但是在目标检测中，杂波数据远远多于目标数据；第二，普通的二分类问题中，两类错分概率是等价的，但是在目标检测中，虚警概率比漏检概率更重要(通常，虚警概率要低于10—3而漏检概率可能达十分之几)。这两点不同导致机器学习中用于分类问题的算法不能直接使用在目标检测问题中。其中，两类样本数量不均衡的问题已经被所提出的仿真目标回波产生器所解决，但是实现虚警可控仍是一个难题。

3.1 传统K-NN算法概述

许多学者都在研究机器学习算法，用于分类和回归问题。K-NN算法是一种简单有效的非参数分类算法，其经常用于许多的模式识别问题。K-NN算法使用训练数据本身直接对测试样本进行分类[16,17]。首先寻找到与测试样本最相似的k个训练样本(称之为近邻)，之后将k个近邻中最主要的类别定为待测样本的类别，其中样本之间相似性度量以距离计算为准。为了获得k个近邻，测试样本需与每个训练样本进行距离计算。

具体算法步骤可描述如下：

xtest ∈Rd

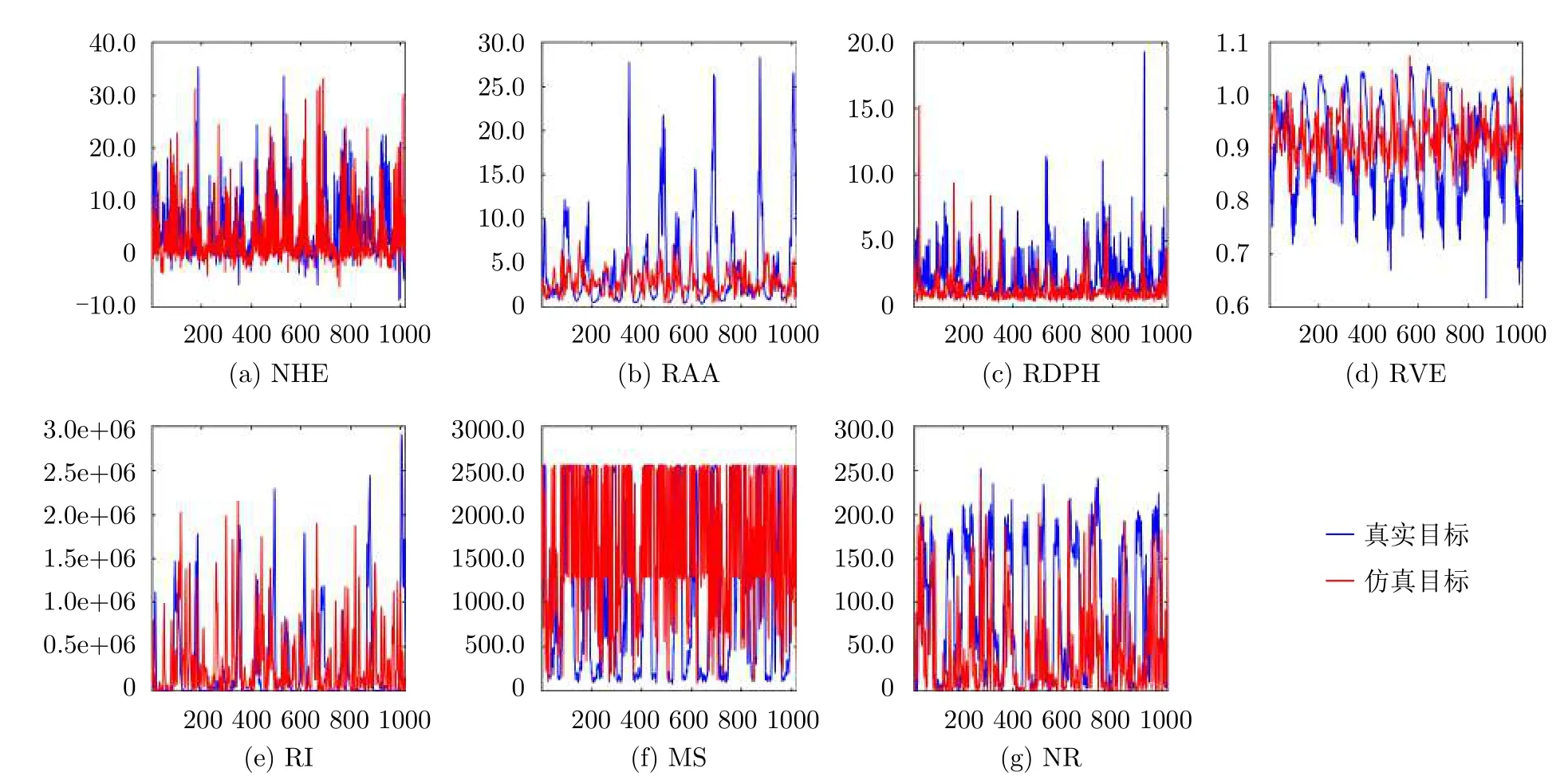
图 1 仿真目标7特征与真实目标7特征对比图Fig. 1 The comparisons of seven features of simulated targets returns and real targets returns

(1) 给出一个测试样本 和训练样本集合Xset，其中，xi是训练集合中第i个训练样本，计算测试样本和每个训练样本之间的欧式距离

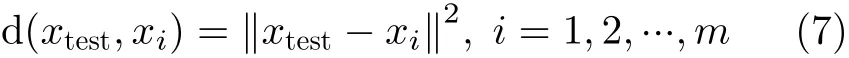
其中，m是训练样本的数目，d(x,y)表示计算x与y之间欧氏距离。

(2) 将所有距离{d(xtest,xi),i=1, 2, ··,m}从小到大进行排序，选取k个最小的距离值{d(xtest,xi1),d(xtest,xi2), ··, d(xtest,xik)}所对应的k个训练样本{xi1,xi2, ··,xik}，此处称之为k个近邻。

(3) 令 li为 训练样本 xi的类标(也可称之为类别)，并认为k个近邻中最主要的类标即为测试样本的类标，即

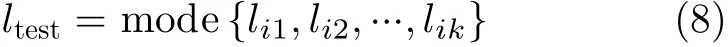
其中， ltest表 示测试样本的类标，操作 m ode{·}表示计算集合中所有元素的众数。

由于简单的判决准则，即测试样本的类标取决于k个近邻中最主要的类标，K-NN算法被广泛使用。但是，在目标检测中，虚警概率和漏检概率是不均等的，往往我们对虚警概率的控制要求更为严格。此外，机器学习算法通常要求两类样本的数目近似相等。所以，机器学习算法中可用于解决二分类问题的算法不可以直接使用在雷达目标检测中。

3.2 基于可控虚警的改进K-NN海面小目标检测

之前的很多关于K-NN算法的研究普遍集中于寻找最优的k值以提高检测器的性能。如果要将KNN算法使用在雷达目标检测问题中，准确地控制虚警概率则是重要而且必不可少的。虽然凸包学习算法[9,11]可以精准地控制虚警概率，但是它只能被用于单分类问题，以及只能在低维空间(n≤3)中使用。因此，凸包学习算法便不再适用于高维空间两分类问题。一种改进的基于可控虚警的K-NN方法被提出，具体过程如下：

(1) 通过雷达接收机获取海杂波时间序列c(n)；

(2) 仿真目标的产生：使用仿真目标回波产生器产生与海杂波数据等量的仿真目标回波数据s(n)；

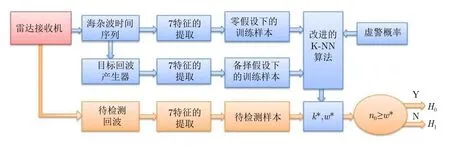
图 2 所提检测器的流程图Fig. 2 The flowchart of the proposed detector

(3) 提取有效特征：对杂波序列c(n)和目标回波序列s(n)分别提取7个有效的特征，构成七维特征向量，并将其组成特征矩阵S0和S1，则训练样本集为S=S0∪S1，其中，S为m×n的矩阵，m=7是特征数量，n是海杂波和仿真目标样本数目之和；

(4) 对于当前测试样本集中的每一个测试样本也提取同样的7特征并构成特征向量，计算其与所有训练样本之间的欧式距离，得到距离向量D；

(5) 将距离向量D中的元素按照从小到大的顺序进行排列，并取k个最小距离值所对应的k个训练样本，构成k近邻；

(6) 计算k近邻中，原本属于海杂波样本S0的数量n0和原本属于目标样本S1的数量n1，其中n0+n1=k；

(7) 设置一个阈值w，若n0≥w，则测试样本被分类为海杂波，否则认为其是目标；

(8) 通过多次实验，经验地选取一个阈值w*，固定其保持不变，改变近邻数目k的取值，使得实现的虚警概率Pfa和预设的虚警概率Pf之间差的绝对值小于一个极小值，将最终符合虚警要求的近邻数记为k*；

(9) 对于每个测试样本，在k*个近邻中，若n0≥w*，测试样本被分为海杂波，否则被分为目标。

图2是所提检测器的流程图，主要分为两个部分：用蓝色表示的离线操作部分和用黄色表示的在线操作部分，红色为共用部分。离线部分包括海杂波的获取、仿真目标回波的产生、零假设和备择假设下两类特征向量的提取和根据虚警要求对应的改进K-NN算法中参数的计算；在线部分包括待检测回波的获取、待检测的特征向量的构成以及判决部分。

4 实验与分析

4.1 实验数据

实验所用数据为20组(4种极化)驻留模式下的实测IPIX[7]海杂波数据，其雷达工作在X波段，fr=1000 Hz，除了第18组和19组数据的距离分辨率为15 m和9 m以外，其余均为30 m。前10组数据采集于1993年加拿大东海岸，测试目标是一个用锚固定的漂浮的直径为1 m的塑料小球，随着海浪上下运动，每组数据的时间序列长度为217，距离单元数目为14；后10组数据采集于1998年在加拿大安大略湖，测试目标是一艘低速运动的小船，每组数据由28个连续距离单元构成，每个距离单元包含60000个脉冲序列。具体的数据信息，如风速(Wind Speed,WS)、有效浪高(Significant Wave Height, SWH)、雷达视线与风速夹角以及目标所在单元和周围影响单元如表1所示。

4.2 检测器性能与分析

在图3中，分别画出了在IPIX雷达数据集上，4种极化下、观测时间为0.512 s的多种检测器平均检测概率对比图。通过比较发现，所提检测器在76组数据上呈现出最优的检测结果，剩下4组也是接近于最优检测结果。可以得出结论，所提检测器具有良好的检测性能和稳定性。在表2中，通过观察各种基于特征的检测器[9,11,12]的平均检测概率可以得知，使用单一特征或少量特征的检测器的性能远差于联合使用多个有效特征的检测器的性能。在图4中，分别画出了在IPIX雷达数据集上，四种极化下、观测时间为1.024 s的多种检测器平均检测概率对比图。通过对比发现，当观测时间从0.512 s提升至1.024 s时，所有检测器的性能均有提升。其中，基于分形的检测器的性能从0.329提升至0.435，它是所有检测器中提升效果最明显的。但是所提出的检测器的性能只从0.851提升至0.892，这是由于天花板效应。因为在观测时间为0.512 s时，所提出的检测器的平均检测概率已经接近于1，所以它只有很小的空间以供性能的提升。

更进一步，为了验证所提方法在多种虚警概率下的更优性能，本文对比了所提检测器和其余检测器在虚警概率为0.01时的检测结果。如表3所示，通过实验表明，所提检测器在更高虚警率下，表现仍旧优异。

除此之外，为了进一步的分析7个特征在检测过程中的贡献，本文设计了7个仅使用6个特征的基于KNN的检测器，即每个检测器分别去掉1个特征。通过这7个基于6特征的KNN检测器与所提出检测器的性能差值来评估这些特征的重要性。具体结果如表4。

其中，性能损失为在相同条件下，所提出的使用7个特征的检测器的检概率减去使用6个特征的检测器的检测概率。由表4的结果可知，当所有特征中去掉RDPH时，对检测性能的影响最大(其中HH极化下性能损失高达5.14%)，其他依次是RI,MS, RAA, NHE, RVE和NR。缺失某个特征后，在4种极化下的性能损失均有不同，不存在某个特征在4种极化下的贡献都最低的情况。当然，也不存在某个特征在每组数据下都表现最优的情况，即各个特征在不同情况下或多或少都对检测结果做出了贡献，所以联合使用多个来自不同域的特征也是很有必要的。总的来说，该检测方法为一个开放的理论框架，允许更多有效且互补的特征加入以提高检测器的性能。

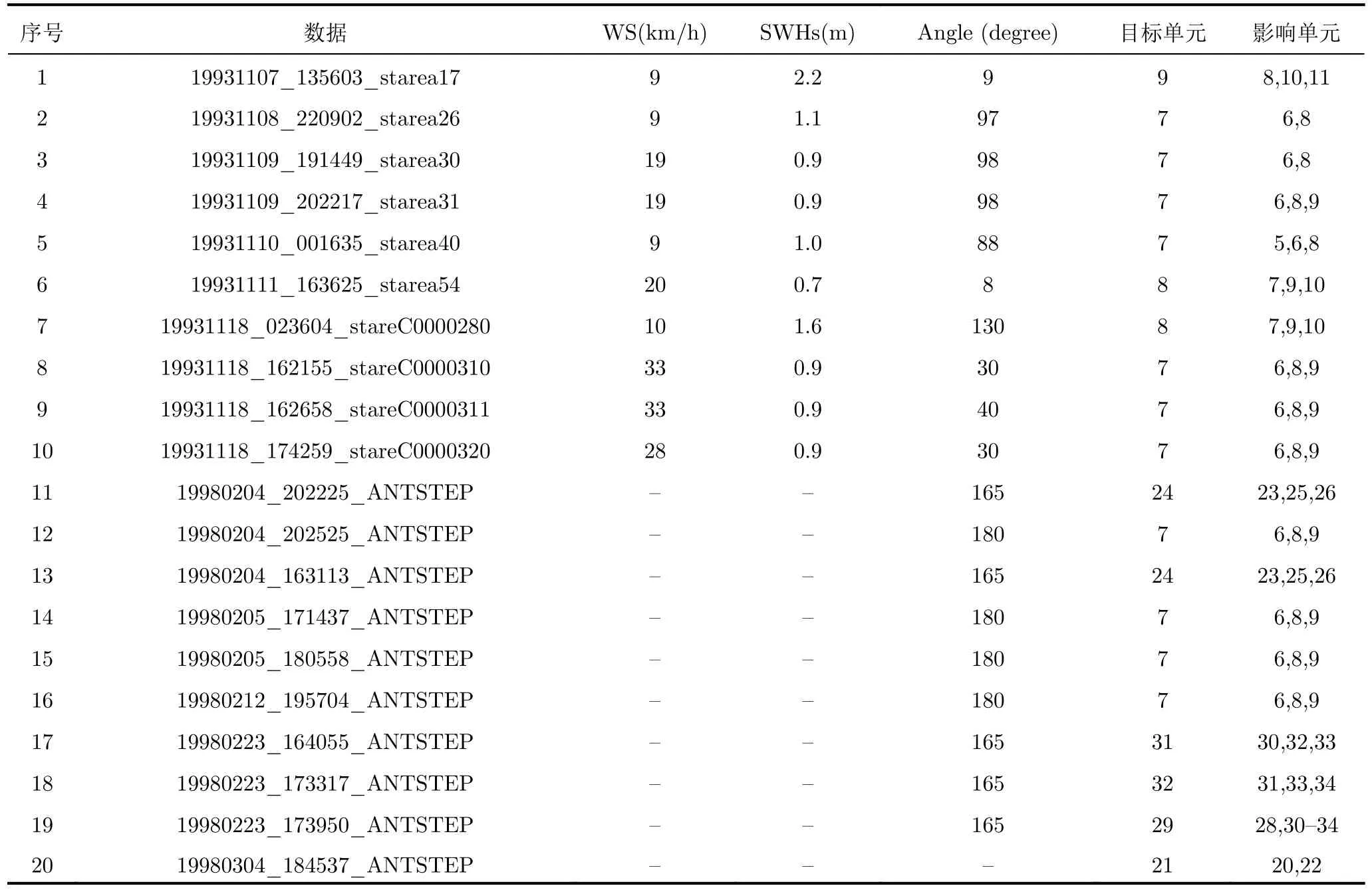
表 1 IPIX数据集描述[10]Tab. 1 Description of IPIX radar database[10]

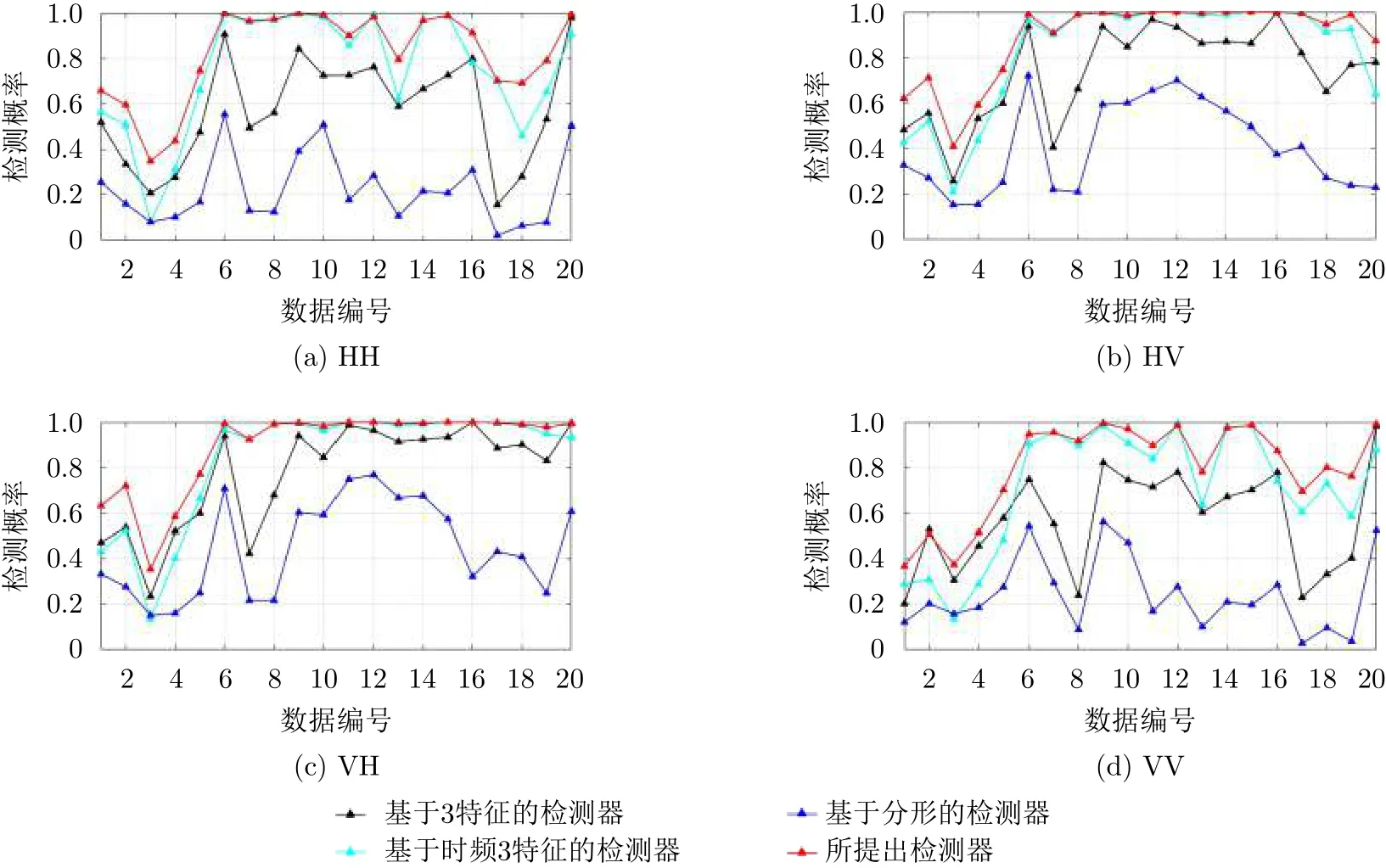
图 3 所提检测器与其余检测器的检测概率Fig. 3 Detection probabilities of the proposed detector and other detectors

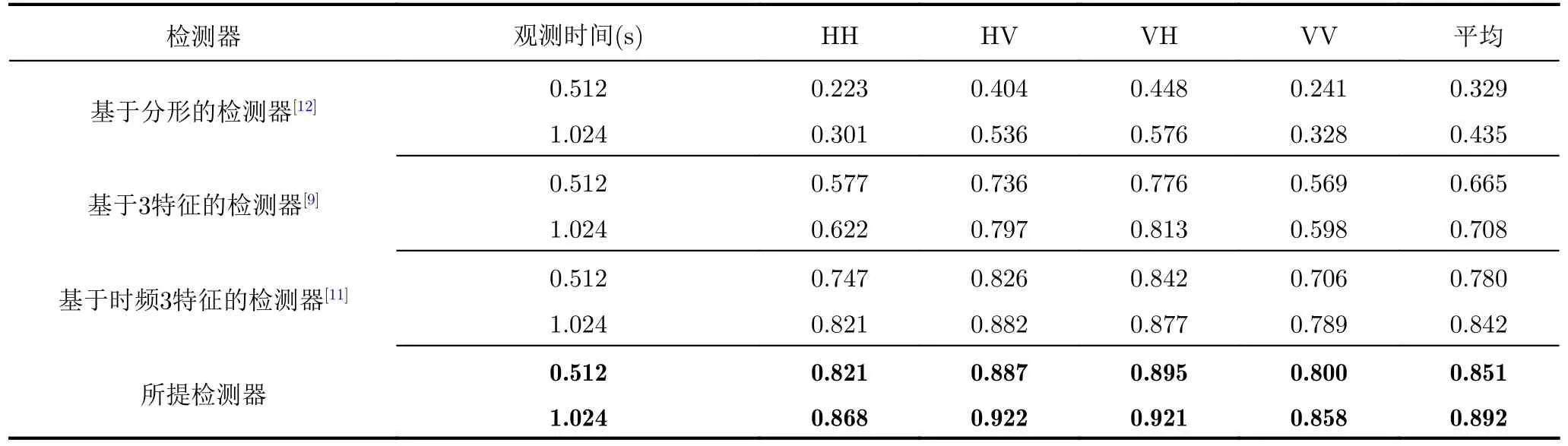
表 2 IPIX数据集上多种检测器的平均检测概率Tab. 2 The average detection probabilities of detectors on IPIX radar database

下面，为了印证本文所提方法对于虚警率的控制情况，图5展示了k值的变化对虚警概率的影响。通过改变k的取值，就可以达到不同的虚警概率。本文中，当预设虚警率为0.01时，实际的虚警与预设的虚警之差的绝对值小于0.001即满足要求；当预设虚警为0.001时，实际的虚警与预设的虚警之差的绝对值小于0.0001即满足要求。最终所提出的检测器在20组IPIX雷达数据集上实现的虚警如表5所示，其中4种极化的平均实现虚警率和所有极化的平均实现虚警率已列出，与预设虚警率相差甚微。由此可见，所提检测器很好地控制了虚警率。

5 结论

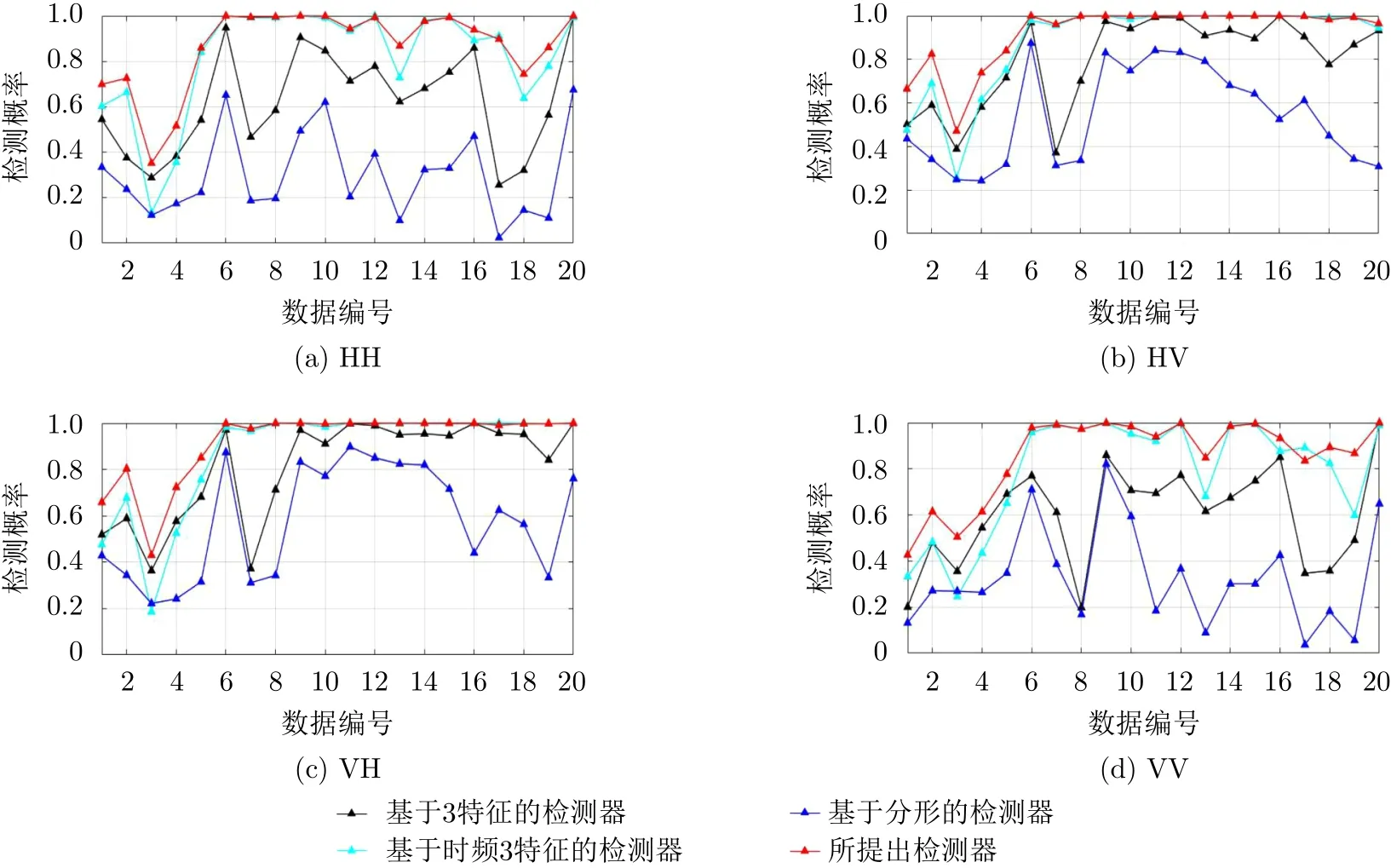
图 4 所提检测器与其余检测器的检测概率Fig. 4 Detection probabilities of the proposed detector and other detectors

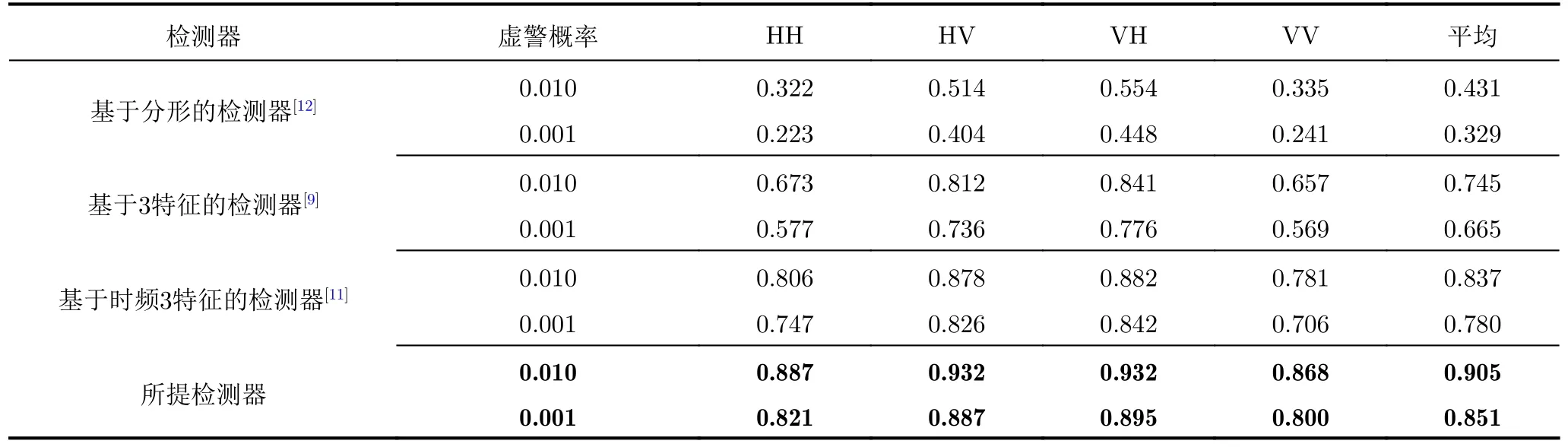
表 3 IPIX数据库中20组数据的平均检测结果对比Tab. 3 The comparisons of average detection results of 20 datasets on IPIX radar database

表 4 基于6特征的KNN检测器在IPIX数据库上20组数据的平均检测结果对比 (%)Tab. 4 The average detection results comparisons of KNN-based detectors using six features at 20 datasets on IPIX radar database (%)

本文提出了一种高维空间中基于可控虚警K-NN的海面小目标检测方法。现有的基于特征的检测方法存在维数限制问题，维数限制问题严重地阻止了更多有效特征在目标检测过程中的使用，更进一步限制了性能的提升。所提检测器很好地解决了上述问题。考虑到普通的二分类算法中两类样本数目均衡的需求，使用一种典型的仿真目标回波产生器可产生与杂波等量的典型的仿真目标回波，为后续检测器的设计起到辅佐的作用，使得目标信息被使用到训练检测器的过程。此外，通过改进机器学习中K-NN算法，实现了目标检测问题中最重要的虚警率可控，即有效地将K-NN算法应用到了目标检测中。最后通过公认的IPIX雷达数据集的验证，本文所提检测器与其余基于单特征或者3特征的检测器相比，具有良好的检测结果和鲁棒性。

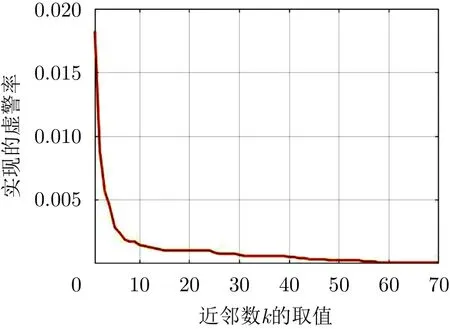
图 5 k值不同时，所实现的虚警率变化图，其中w*=3Fig. 5 Realized false alarm rate when k takes different values, where the w*=3

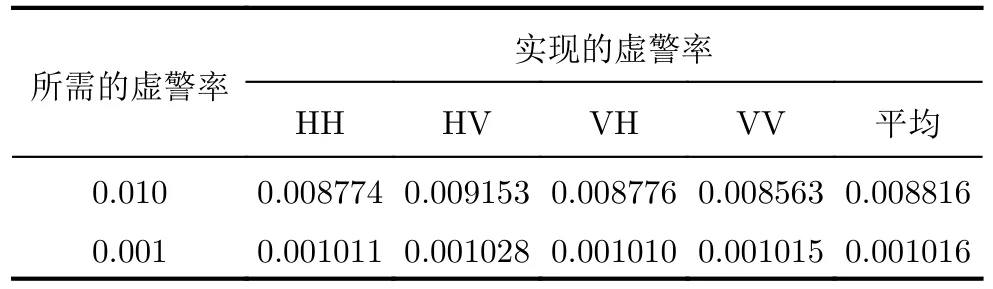
表 5 所提检测器在20组IPIX雷达数据集上实现的虚警概率Tab. 5 The realized false alarm rate of the proposed detector of 20 datasets on the IPIX radar database