近场非圆信号参数快速估计算法

宋嘉奇 陶海红

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

根据天线手册[1]，在天线阵列中心到 2 D2/λ的空间范围内的信号源被认为是近场源，其中D是天线孔径， λ为工作波长。大多数参数估计问题均假设信号源位于天线远场区域，而在很多实际应用中，存在感兴趣的信号位于天线阵列近场区域这一情况，此时应用传统远场的参数估计算法会导致性能下降，甚至完全失效。

随着阵列信号处理技术的不断发展，近场源的参数估计问题越来越受到广大学者的关注。文献[2]提出了一种角度-距离的两维MUSIC(MUltiple SIgnal Classification)方法，有效实现了近场源的超分辨参数估计，但两维谱峰搜索的运算量巨大。文献[3]引入了4阶累积量矩阵，并基于ESPRIT(Estimation of Signal Parameter via Rotational Invariance Technique)算法提出了总体最小二乘的ESPRIT-like算法，然而构建累积量矩阵同样需要耗费巨大的运算量。此外，文献[4]提出了一种经典的基于2阶统计量的GESPRIT(Generalized ESPRIT)近场源定位算法。但此算法存在一半的阵列孔径损失，因此估计精度有所降低并且可估计信源的个数减少了1/2[5]。

非圆信号广泛应用于雷达、通信等领域，如BPSK(Binary Phase Shift Keying), PAM(Pulse Amplitude Modulation)以及ASK(Amplitude Shift Keying)等。近年来，大量参数估计算法采用非圆信号以提高估计性能[6,7]，但将非圆信号应用到近场源定位问题中的相关工作还比较少。文献[8]利用非圆信号和对称线阵的性质，提出了一种实值非圆降秩算法(Real-Valued Non-Circular RAnk RE-duction, RVNCRARE)。文献[9]将多维搜索问题解耦成两个一维搜索问题，依次估计近场源的角度和距离参数，有效避免了多维搜索。文献[10]提出了一种非圆GESPRIT(Non-Circular Generalized ESPRIT, NCGESPRIT)算法，首先利用信号非圆特性构造增广的阵列数据矩阵，其次利用GESPRIT方法估计出信号的到达角度，最后通过对距离谱函数的一维搜索得到信源的距离估计。该算法只需构造2阶统计量矩阵和一维搜索，运算复杂度低，同时避免了GESPRIT算法带来的孔径损失。西北工业大学的况梅东等人[11]在此基础上提出了针对部分极化的非圆近场参数估计算法。宁波大学的陈华等人[12,13]利用对称均匀线阵以及非圆信号特性提出了两种远近场混合源的非圆参数估计新方法。本文基于降秩定理和多项式求根方法，对近场目标的角度和距离参数分别进行估计，有效降低了构造高阶统计量和多维参数搜索所带来的计算复杂度。通过与GESPRIT算法和NCGESPRIT算法的性能对比，证明所提算法增加了可分辨信号源的个数，参数估计性能较好，且运算复杂度较低。

2 近场源信号模型

假设在近场区域存在K个独立窄带非圆信号同时照射到空间阵列上，空间阵列如图1所示，由N =2M +1个全向天线阵元组成，各个阵元的位 置 坐 标 可 以 表 示 为[-Md,-(M -1)d,··,0,··,(M -1)d,Md]， 其中 d为阵元间距。

不失一般性，选取对称阵列的中心阵元(0号阵元)为参考阵元，则 t时 刻第 m个阵元的接收信号xm(t)可以表示为

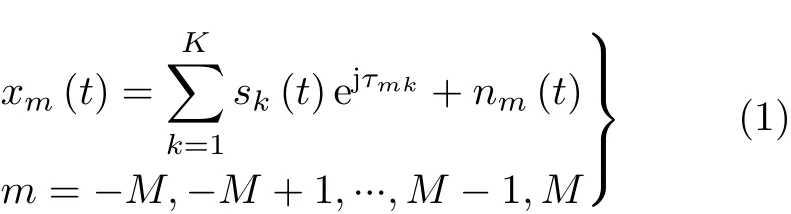
其中， sk(t)表 示第 k 个 入射信号， nm(t)为 第 m个阵元在 t时刻的噪声， τmk表 示 sk(t)在 第 m个阵元相对于参考阵元的传播时延，具体的传播时延表达式为

其中， θk和 rk是 sk(t)的角度和距离参数。由于传播时延表达式过于复杂，不便于计算，根据菲涅尔近似[2]，传播时延可以近似为

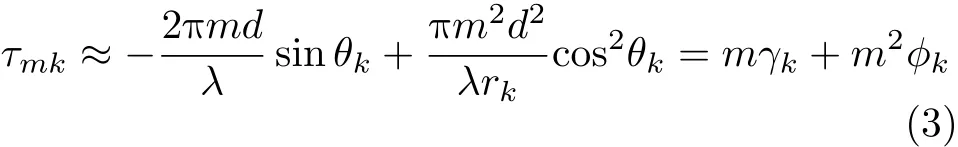
其中，

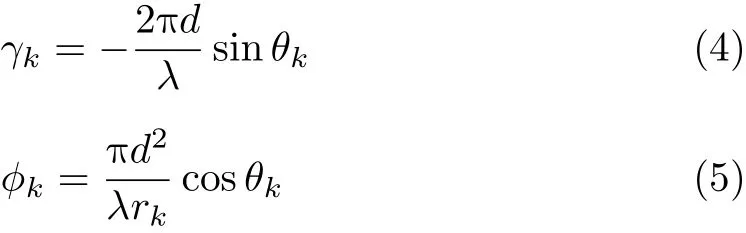
因此，式(1)的接收信号 xm(t)可以简化为

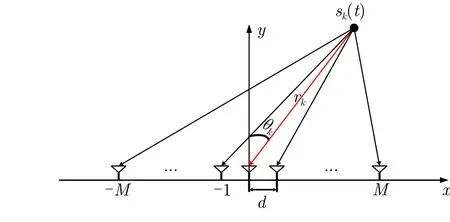
图 1 近场参数估计示意图Fig. 1 Schematic diagram of near-field parameter estimation

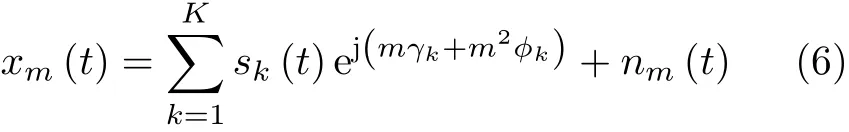
将天线阵列接收信号的数据改写成矩阵形式，可以表示为

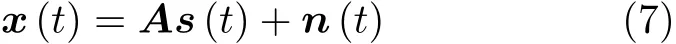
其中，x(t)=[x-M(t),x-M+1(t),··,x0(t),··,xM-1(t),xM(t)]T为阵列接收数据矩阵，上标T表示对矩阵取转置。n(t)=[n-M(t),n-M+1(t),··,n0(t),··,nM-1(t),nM(t)]T为 加性噪声矩阵。 A表示阵列的导向矢量矩阵，其详细形式为

近 场 导 向 矢 量a(θk,rk)=[ak,-M,ak,-M+1,··,s(t)=[s1(t),s2(t),··,sK(t)]T表示近场非圆信号矩阵，根据入射信号的非圆特性，信号矩阵 s (t)可表示为

其 中 ， s0(t)=[s0,1(t),s0,2(t),··,s0,K(t)]T∈ RK×1,s0,k(t) 是 sk(t) 零 初相的实信号。对角矩阵Ψ =diag{ejψ1,ejψ2,··,ejψK} , ψk为信号 sk(t )的初相。

3 近场非圆信号快速参数估计算法

为了充分利用信号的非圆特性，对阵列接收的多快拍数据进行扩展处理，将阵列输出矩阵与其共轭进行拼接，得到增广的阵列接收数据矩阵。

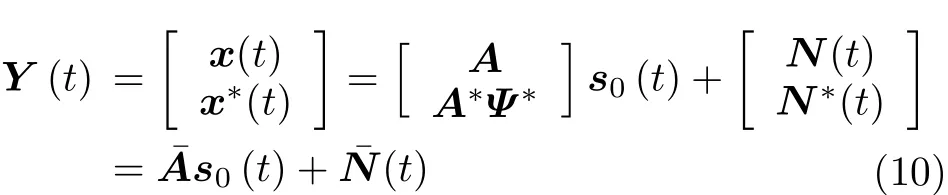
其中，上标*表示对矩阵取共轭， A¯ =[A A*Ψ*]T，表示扩展的导向矢量矩阵A¯=[a¯(θ1,r1,ψ1),a¯(θ2,r2,ψ2),··,a¯(θK,rK,ψK)], N¯(t)=[N(t) N*(t)]T

其中， US和 UN分别为特征向量张成的信号子空间和噪声子空间， Λs为 K个主特征值构成的对角矩阵， ΛN为 剩余 2N -K个次特征值构成的对角矩阵。传统子空间算法的思路是在角度-距离两维参数域 (θ ,r)中 进行谱峰搜索，搜索下列谱函数的 K个最小值来得到信号源的位置参数。

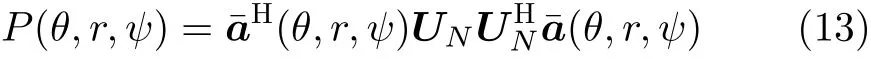
但高维谱峰搜索的运算复杂度大，为了有效降低算法运算复杂度，本文提出了基于多项式求根的近场非圆信号源快速参数估计算法，对扩展的导向矢量矩阵进行解耦，然后利用多项式求根方法依次对信号源的角度和距离进行估计。

3.1 角度估计

首先，对近场信号源的角度进行估计，根据阵列的对称性对导向矢量矩阵进行解耦，可得

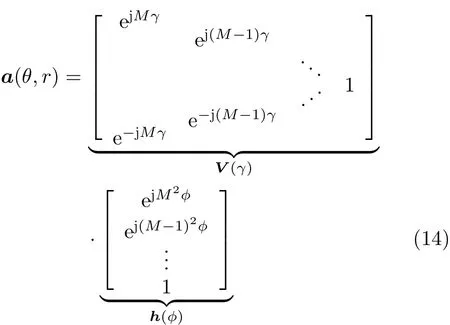
故扩展的近场导向矢量矩阵可以改写成为

矩阵 C (θ)的维数取决于阵元个数，若阵元个数N =2M +1， 则矩阵 C (θ)为 2( M +1)× 2(M +1)维。以三阵元线阵为例，此时 z =ejγ, γ =-2πd sin θ/λ

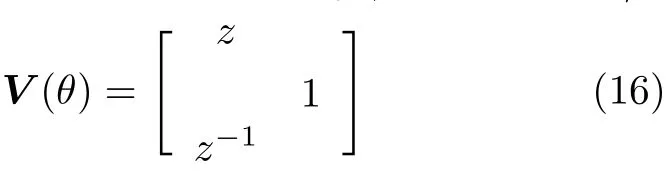
由于 UN的 矩阵维数为 (2 N ×(2N -K))，令UN1=UN(1:N,:) , UN2=UN(N +1:2N,:)。则

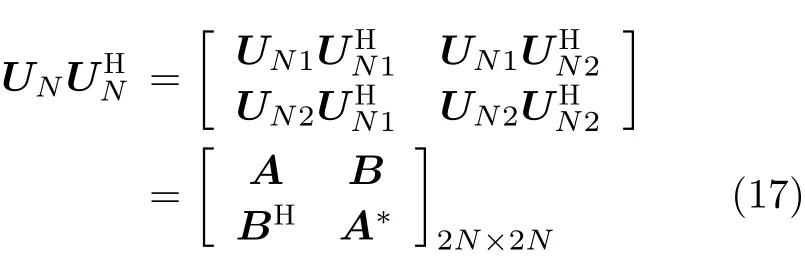
求得 M矩阵的行列式表达式后，对多项式det(C(z))=0进行求解，寻找单位圆内最靠近单位圆的 K 个点，即为所求的 z的值 zˆk，从而根据式(20)反推出近场源的角度估计值：

定理3 设Cφ是Βψ,0上的有界复合算子，则Cφ在Βψ,0上下有界当且仅当存在ε>0，使得Gε=φ(Ωε)是Bn上的一个样本集，其中

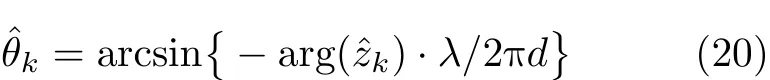
当阵元数增多时，矩阵行列式的表达式可以通过矩阵分块来求得

除此之外，也可以利用MATLAB软件的符号函数syms来计算。

3.2 距离估计

根据信号的非圆特性，近场的导向矢量矩阵可以解耦为

表 1 矩阵M中的元素Tab. 1 Elements of matrix M

由于矩阵 Q为2阶矩阵，其行列式的表达式很容易得出，利用多项式求根的方法找出最靠近单位圆的K个估计值 fˆk，再根据式(29)反推出信号源的距离参数。

3.3 算法流程

(1) 获取接收数据协方差矩阵 R；

(2) 对 R矩阵进行特征值分解；

(3) 构造 M 矩阵，根据式(19)求出 d et(M(z))的表达式；

(4) 求解 d et(C(z))=0，选取单位圆内靠近单位圆的 K 个，根据由反推出；

(5) 构造 Q矩阵，根据式(25)求出 d et(Q(z))的表达式；

4 性能分析与实验仿真

4.1 性能分析

4.1.1 可估计信源数分析

本节主要讨论GESPRIT算法[4]、NCGESPRIT算法[10]以及本文所提算法可分辨信号源的最大数目。为便于分析，假设3种算法均采用阵元数为N =2M +1的均匀线阵。由于噪声子空间至少需要一个特征向量所张成，且GESPRIT算法会损失1/2的阵列孔径，故GESPRIT算法最多可分辨 M个信号源；NCGESPRIT算法与本文所提算法利用了信号的非圆特性，扩展了信号子空间，没有阵列孔径损失，而需要张成噪声子空间的特征向量不变，因此可分辨最多 2 M个信号。

4.1.2 运算复杂度分析

在本节的计算复杂度分析中，只讨论运算量耗费较大的几部分，其中包括统计量矩阵的构建、特征值分解以及谱峰搜索。假设角度和距离的搜索范围分 别 为 θ ∈[-90°,90°] 和 r ∈ [0.62(D3/λ)1/2,2D2/λ]，其中搜索步长为 Δθ和 Δr。阵列的阵元数目为N，快拍数为L。GESPRIT算法估计信号源的角度和距离参数需要构建两个 N ×N的2阶累积量矩阵，进行两次特征值分解，以及两次谱搜索。NCGESPRIT算法则需要构建一个 2 N ×2N的2阶累积量矩阵，进行一次特征值分解和两次谱搜索。本算法构建的是一个 2 N ×2N的2阶实值累积量矩阵，也需要进行一次特征值分解，无需谱峰搜索。表2详细给出了3种算法各种运算所需的运算量。

由表2可以看出，所提算法虽然在构造统计量矩阵与特征值分解两部分运算量略高于GESPRIT算法，但本文算法无需谱峰搜索，有效降低了算法的运算复杂度，而NCGESPRIT算法所需的运算复杂度最高。

4.1.3 近场非圆信号参数估计的克拉美罗界

将未知参量写成矢量记作 η =[θTrTρTσn2]T。其中，θ =[θ1,θ2,··,θK]T是 DOA参数矢量，r =[r1,r2,··,rK]T是距离参数矢量，

根据近场非圆信号模型以及非圆复高斯信号的假设，费舍尔信息矩阵具体表达形式为[15]

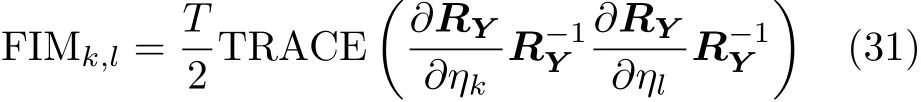
其中，RY是 Y (t)的协方差矩阵。由于本文仅关心信源的位置参数 θ和r，因此根据文献[15]的式(10)可得

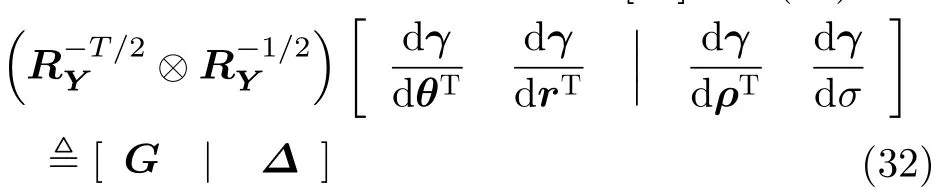
对于非圆信号，文献[15]的式(15)由式(33)替换

表 2 算法运算复杂度比较Tab. 2 Algorithm complexity comparison

相应地，可以继续推导出

4.2 实验仿真

为了验证本文所提算法的有效性及参数估计性能，将其与GESPRIT算法[4]以及NCGESPRIT算法[10]进行实验仿真对比。在下列仿真实验中，假设天线阵列是由7个各向同性阵元(M =3)组成的对称均匀线阵，阵元间距 d =λ/4。信源入射到阵列的信号均为等功率、统计独立的BPSK信号。参数估计性能通过均方根误差来衡量，均方根误差的表达式为

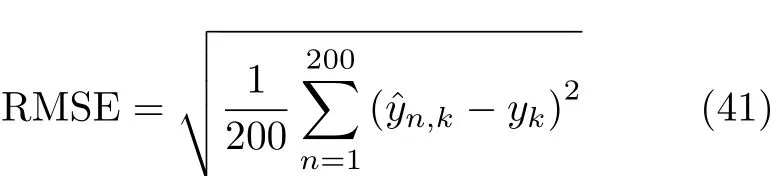
其中， yk表 示信号源的角度参数 θk或 距离参数 rk，示第 n次 试验中本算法对 yk的估计值，总的蒙特卡洛试验次数为200。

4.2.1 仿真实验1

仿真实验1主要研究信噪比对参数估计性能的影 响 。 假 设 信 号 源 位 于 ( -30°,2λ) , (- 1 0°,3λ),(20°,4λ)，快拍数为200。信噪比以步长5 dB从0 dB到40 dB逐渐增加。图2展示的是DOA和距离估计的均方根误差随信噪比变化的曲线，同时给出了近场非圆信号参数估计的CRB。显然可以看出，由于利用了信号的非圆信息，所提算法与NCGESPRIT的DOA估计性能几乎一致，距离估计性能略优于非圆GESPRIT，且两者均能很好地趋近CRB。另外，所提算法与NCGESPRIT的性能均明显优于传统的GESPRIT算法。

4.2.2 仿真实验2

仿真实验2主要研究快拍数对参数估计性能的影响。信号源参数与仿真实验1相同，信噪比固定为20 dB，快拍数从10～1000变化。3种算法的估计性能及CRB随快拍数的变化曲线图如图3所示。可以看出，随着快拍数的增加，角度和距离的估计性能逐渐提高，本文所提算法的RMSE曲线更靠近CRB，说明所提算法具有更高的参数估计精度。此外，由于本文所提算法与NCGESPRIT算法充分利用了信号的非圆特性，阵列的虚拟孔径增大，其参数估计性能明显优于传统的GESPRIT算法，且RMSE曲线能够很好地趋近CRB。

4.2.3 仿真实验3

图 2 RMSE-信噪比曲线图Fig. 2 RMSE-signal to noise ratio curve

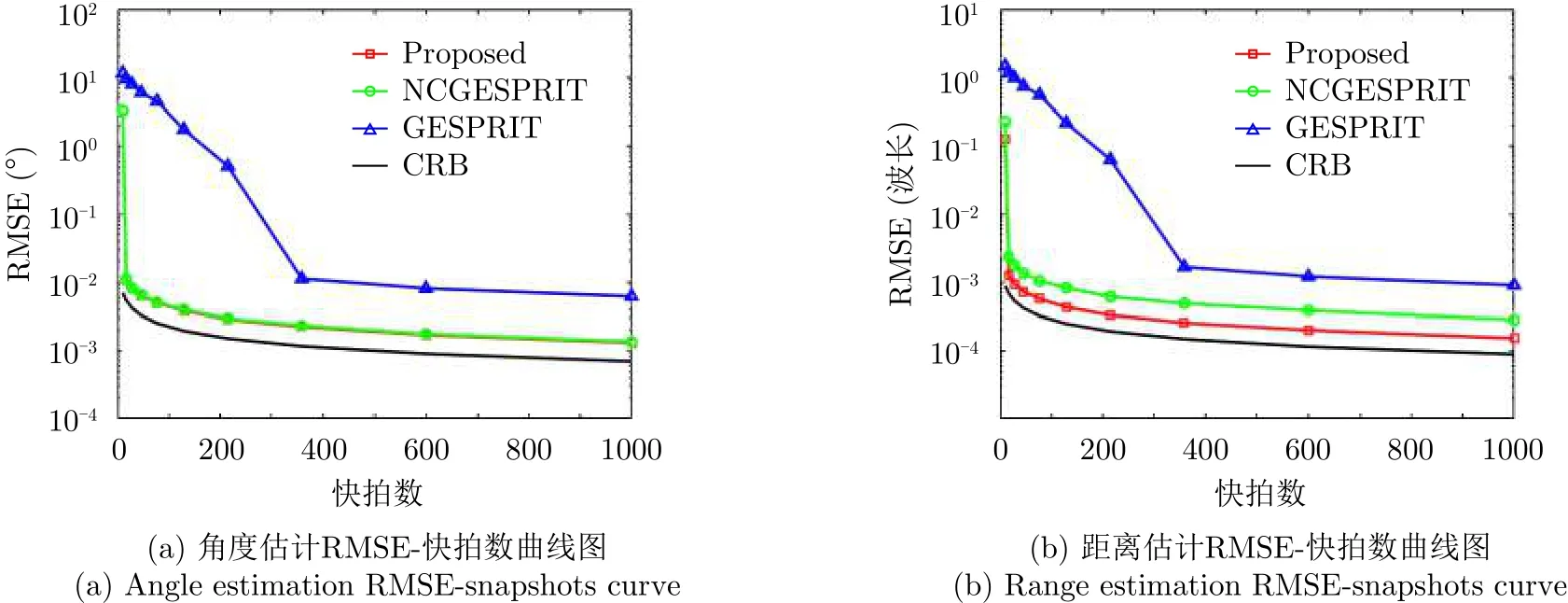
图 3 RMSE-快拍数曲线图Fig. 3 RMSE-snapshots curve

仿真实验3中，对3种算法的运算复杂度进行比较。假设近场区域仅存在一个信号源，信噪比为20 dB，角度与距离的搜索步长分别为1°和 0 .01λ，图4为算法运行100次的平均时间随阵元个数变化的曲线(CPU：酷睿i5 2.4 GHz，内存：8 G)。可以看出，阵元数少的时候，所提算法与GESPRIT运算量相当，随着阵元数的增加，本算法的运算复杂度略高于GESPRIT算法，但始终低于NCGESPRIT算法。这是由于所提算法和NCGESPRIT算法构造的扩展协方差矩阵的维数是GESPRIT算法的两倍，因此阵元数增多时所提算法的运算复杂度略高于传统GESPRIT算法。同时，由于本文所提算法采用了多项式求根技术，有效避免了谱搜索，因此运算复杂度较之于NCGESPRIT相比计算复杂度更低。

5 结论

图 4 三种算法的运算时间比较Fig. 4 Comparison of operation time of three algorithms

本文基于对称的均匀线阵提出了一种新的近场非圆信号的快速估计算法。通过对近场阵列的多维参数解耦与多项式求根方法，近场源的DOA和距离参数依次估计得出。本算法避免了高阶统计量的计算与谱峰搜索，有效地降低了运算量，并利用非圆信号提升了参数估计的自由度。通过仿真实验结果验证可得本算法能够在提升参数估计精度的同时将运算复杂度保持在较低水平，同时可检测信号源数目也得到提升。