带有攻角约束的吸气式高超声速飞行器反步法控制①

马晓川，陈 康，杜昊昱，闫 杰

(西北工业大学 航天学院，西安 710072)

0 引言

吸气式高超声速飞行器具有快速全球打击、超音速突防、低成本空天往返等优点，在军事和民用两个方面都有很好的应用价值，是未来飞行器研究和发展的热点。受高超声速气流的作用，吸气式高超声速飞行器受到的气动力呈现较强的非线性和不确定性[1]。而发动机-机身一体化的结构造成了推力与气动力矩耦合[2-3]。细长体结构的气动外形又降低了飞行器的刚度，飞行控制中的气动弹性问题更加突出[4-5]。针对于吸气式高超声速飞行器的特点， 控制[6]、滑模控制[7-8]、自适应控制[9-10]等控制方法被应用于高超声速飞行器控制问题的研究。

反步法是处理吸气式高超声速飞行器非线性控制问题的有效方法。文献[11]使用神经网络近似吸气式高超声速飞行器模型中的非线性未知项，然后使用反步法设计了飞行控制器，而且在控制器设计中引入附加系统来补偿执行机构饱和对控制系统的影响。文献[12]针对吸气式高超声速飞行器的非线性和不确定性设计了反步控制器，对飞行器模型的不确定项用干扰观测器进行估计与补偿。文献[13]在反步控制器设计中，使用干扰观测器对吸气式高超声速飞行器模型中的不匹配不确定性进行了补偿。文献[14]使用二阶指令滤波器进行高超声速飞行器的反步控制器设计，提高了控制系统对扰动的抑制能力。文献[15]使用反步法设计了分布式鲁棒控制器，通过将反步控制和信号补偿结合起来构成一个鲁棒控制器的方式，简化了系统处理的复杂性。文献[16]设计了吸气式高超声速飞行器的反步容错控制器，对执行机构的时变故障进行了补偿。

发动机进气道不启动现象是一个严重影响吸气式高超声速飞行器飞行安全的问题。进气道不启动是因为发动机燃烧室内压力上升或者激波面与发动机隔离室分离而引起的[17-18]。当进气道不启动时会出现发动机推力骤减甚至发动机关机的现象。又因为吸气式高超声速飞行器发动机-机身一体化的独特结构所造成的推力和气动力的耦合，发动机推力骤减或消失后会在飞行器前部诱发抬头附加力矩。诱发的抬头力矩会改变飞行器的静稳定性或加深飞行器的静不稳定性，造成飞行器控制系统的失效[19]。因此，吸气式高超声速飞行器飞行时需要避免进气道不启动。文献[20-21]表明，进气道不启动与飞行器的攻角有关。这就意味着在飞行过程中，对攻角的限制可有效的避免发动机的不启动现象。基于通过限制攻角来避免进气道不启动的思想，Famularo等[22]在自适应控制器的基础上，增加了状态限制机制，当飞行器攻角超出边界后，限制机制对控制器指令进行修正，实现对攻角的限制。许斌等[23]在反步法控制中引入输入受限滤波器来限制攻角虚拟指令，并利用障碍Lyapunov函数约束攻角与虚拟指令之间的误差，从而达到攻角限制的目的。郝安等[24]在控制吸气式高超声速飞行器时，让飞行器跟踪预设攻角指令，并用鸭翼补偿飞行器攻角限制带来的升力不足的方法保证攻角在允许范围内运动。

针对高超声速飞行器的攻角限制问题，本文使用反步法设计了吸气式高超声速飞行器的控制系统。并在反步法的基础上增加了补偿控制器。补偿控制器在攻角超出预定阈值时对虚拟指令和参考值指令的修正以实现对攻角的限制作用。在以往使用反步法进行状态限制方法中，反步法与障碍Lyapunov函数结合实现对状态的约束作用[23，25-26]。这种方法在状态接近障碍函数边界时会产生较大的控制信号，而本文提出的使用补偿控制器修正控制信号的方法，则避免了这一问题。另外，为了提高飞行器对外部扰动影响，例如风扰动，采用了扩展观测器对外部扰动进行估计和补偿。最后通过数值仿真计算，验证了该控制方法的有效性。

1 高超声速飞行器纵向动力学模型

高超声速飞行器的纵向非线性动力学模型可表示成如下非线性微分方程组：

(1)

其中，状态V、γ、α、ω分别为飞行器的速度、航迹倾角、攻角和俯仰角速度；m和I分别为飞行的质量和转动惯量；g为重力常数；P、D、L、M分别为作用在飞行器上的推力、阻力、升力和俯仰力矩。根据文献[27]，飞行器的气动力和力矩可表示为攻角α与舵偏δ的函数关系式：

(2)

其中，

(3)

飞行器运动时攻角比较小，所以sinα≈α。同时，忽略掉升降舵上的升力，高超声速飞行器纵向姿态运动模型可以近似为严反馈形式：

(4)

其中，

(5)

(6)

严反馈模型中的d1、d2、d3是模型不确定性引起的扰动。模型的输入是舵偏δ，输出是航迹倾角γ。控制系统的设计目的是基于严反馈模型设计高超声速飞行器的航迹倾角跟踪控制器，并且控制器能保证飞行器在跟踪航迹倾角的过程中攻角被限制在预定的范围内。

2 控制系统设计

2.1 反步法控制器设计

(1)航迹倾角回路控制

定义航迹倾角控制误差：

z1=γ-γd-λ1

(7)

式中γd为输入的航迹倾角参考指令；λ1为对控制量的补偿信号。

在传统的反步控制其中，误差的定义不含有补偿信号。控制器驱动飞行器状态γ跟踪指令γd。当加入补偿信号λ1后，在补偿器工作时，控制器则驱动状态γ跟踪修正后的指令γd+λ1。对z1求导：

(8)

设计虚拟控制指令：

(9)

式中c1为一个正数。

(10)

其中，b11、b12、ε1、κ1为观测器参数且均为正数，函数Γ(eγ，ε1，κ1)表示为

(11)

为了解决反步法控制器设计中“微分爆炸”，使用一阶低通滤波器对虚拟指令进行估计。

(12)

式中η1为正数。

定义虚拟指令与估计指令的误差：

y1=αd-αc

(13)

定义攻角控制误差：

z2=α-αd-λ2

(14)

式中λ2为补偿器输出的补偿信号。

把式(13)和(14)代入式(8)，得：

(15)

把虚拟控制律式(9)代入式(15)：

(16)

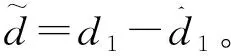
(2)攻角回路控制

对攻角控制误差z2求导：

(17)

设计虚拟控制指令：

(18)

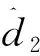
干扰观测器为：

(19)

式中b21、b22、ε2、κ2均为正数。

让虚拟控制指令ωc经过一阶低通滤波器：

(20)

式中η2为正数。

定义虚拟指令与估计指令的误差：

y2=ωd-ωc

(21)

定义俯仰角速度控制误差：

z3=ω-ωd-λ3

(22)

把式(21)、式(22)代入式(17)：

(23)

把虚拟控制律式(18)代入式(23)：

(24)

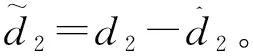
(3)俯仰角回路控制

对俯仰角速度控制误差求导：

(25)

选取控制律：

(26)

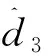
干扰观测器为

(27)

式中b31、b32、ε3、κ3均为正数。

把控制控制律式(26)和式(27)代入式(25)得：

(28)

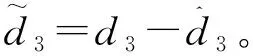
2.2 补偿器设计

在反步法控制中，控制器驱动系统状态跟踪中间控制信号αd和ωd，当误差信号收敛并稳定后，系统完成对参考指令的跟踪。因此，系统的运动状态主要由中间控制信号决定。当系统状态超出限制范围内，可通过对中间控制信号的修正完成对状态的限制控制。基于这种思想，在上述的反步法控制中的每个误差变量的定义中引入了相应的补偿变量。当攻角超出限制边界时利用补偿器对中间控制信号的修正来实现对攻角的限制。而当攻角运行在允许范围内，补偿器不在起作用。控制器变成传统的反步法控制器，保证控制系统对参考指令的跟踪。补偿器设计为

(29)

补偿器输入uλ为

(30)

式中k1、k2、k3、k4为补偿器参数且均为正数；αmax与αmin分别为令补偿器启动的攻角最大阈值和最小阈值。

因为攻角在超出补偿器启动值后才会对控制信号进行修正。因此，补偿器启动的最大阈值要小于攻角限制的上边界值，而最小阈值要大于攻角限制的下边界。这样设置阈值保证在动态响应过程中攻角不超出限制边界。

3 稳定性分析

定义Lyapunov函数：

(31)

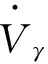
(32)

式(30)中的uλ根据攻角状态值会有不同的表达形式。当αmin≤α≤αmax时，uλ=0，在这种情况下控制器变为传统的反步法控制器。文献[12]已分析了这种条件下控制系统的稳定性。当α>αmax时，uλ=αmax-α。此时，对式(13)和(14)进行变换并代入uλ，得：

uλ=αmax-z2-y1-αc-λ2

(33)

把式(33)代入式(32)，并将括号展开：

(34)

考虑任意两个紧集

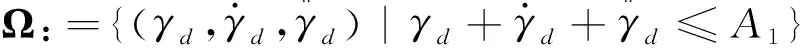
Λ：=

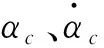
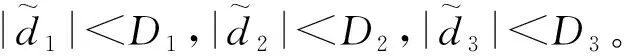
则式(34)满足：

(35)

对式(35)进行缩放：

(36)

整理式(36)：

(37)

选取参数：

(38)

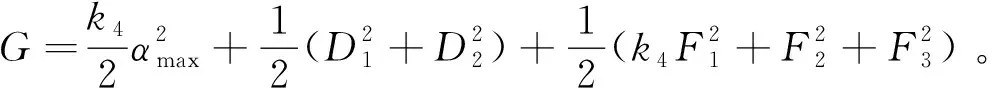
式(37)可进一步表示为

=-2m0Vγ+G

(39)

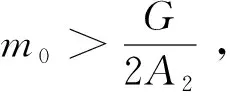
4 系统仿真与分析

通过数值仿真来验证本文提出控制方法的有效性。仿真中使用式(1)描述的非线性模型。模型中的气动力数据来自文献[27]。文献[27]并没有给出发动机进气道不启动的攻角条件，但为了验证控制器效果，假设在飞行器速度为8Ma时，引起进气道不启动的攻角边界为[-5°，5°]。速度控制不在本文讨论的范围内，但为了保证控制系统的完整性，在仿真中使用文献[12]提出的速度控制器来稳定飞行器速度。飞行器初始状态由表1给出。

表1 飞行器初始状态Table 1 Initial state values of the vehicle

仿真中，使用如下二阶滤波器生成航迹倾角参考指令：

(40)

滤波器的阻尼比ζ为0.9。滤波器的输入是幅值为10°的阶跃信号。飞行器利用纵向气动升力改变航迹倾角γ，而纵向升力主要由飞行器攻角提供。这就意味着过大或者过快的航迹倾角指令都会造成攻角超出限定边界。因此，利用滤波器频率ωn的变化来调节指令速率。在限定指令幅值的条件下，通过对不同速度率航迹倾角指令的跟踪来说明控制器对攻角α的限制效果。另外，为了消除补偿器延时和响应过程中信号超调的影响，补偿器的阈值设定为4.7°和-4.7°。阈值范围包含在气道不启动的攻角边界内。同时在仿真中加入幅值为1°，频率为0.05 rad的正弦风攻角来验证控制系统对外界扰动的补偿能力。

仿真中，使用不带攻角限制补偿器的控制方法和带有攻角限制补偿器的控制方法进行对比。图1和图2分别给出了两种控制方法在不同ωn条件下航迹倾角响应曲线和攻角响应曲线。

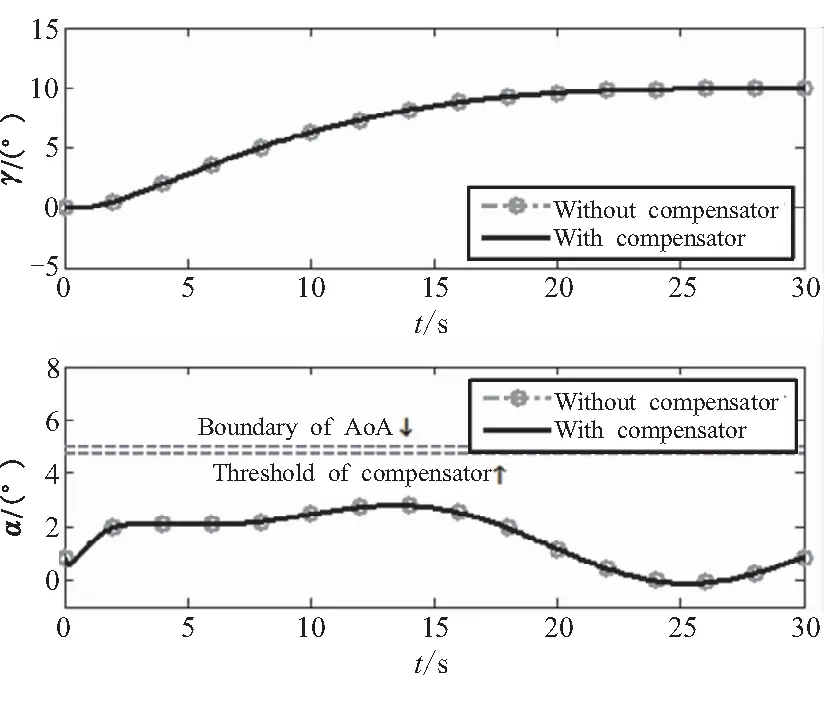
图1 ωn=0.3时的航迹倾角和攻角响应Fig.1 Response of flight path angle and angle of attack when ωn=0.3

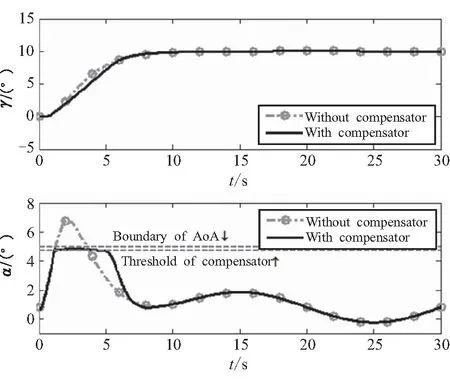
图2 ωn=0.5时的航迹倾角和攻角响应Fig.2 Response of flight path angle and angle of attack when ωn=0.5

图1的曲线是ωn=0.3时的仿真结果。在ωn=0.3时，两种控制系统的航迹倾角响应和攻角响应完全重合。因为飞行器攻角没有达到补偿器阈值，所以在控制过程中，补偿器并没有被触发。即在补偿器不工作时，补偿器对闭环控制系统不产生任何影响。图2中的曲线是ωn=0.5时的仿真结果。在ωn=0.5时，两种控制系统的航迹倾角响应在稳态时曲线重合和，即这两种控制器的稳态特性相同。在航迹倾角响应的上升过程中，带有攻角补偿器的控制系统响应略慢于不带补偿器的控制系统响应。从攻角响应曲线上看，带有补偿器控制系统的攻角被限制在补偿器阈值附近，且在攻角边界之内。而不带补偿器控制系统的攻角响应则越过攻角边界。因为补偿器限制了攻角幅值，即限制了飞行器的纵向过载，所以带有补偿器控制系统的航迹倾角响应在上升过程中会略慢一些。图1和图2中，攻角α响应在稳态阶段并没有收敛到常值状态，这是因为飞行器受到风攻角扰动后，飞行器需要通过改变攻角产生气动力和力矩来抵消风攻角的扰动作用。

下面则以当ωn=0.5时带有补偿器控制方法的仿真结果说明补偿器的工作机制以及控制系统中其他信号的特性。首先分析攻角控制回路。在攻角控制回路中，控制器驱动攻角跟踪控制信号αd+λ2。当攻角在补偿器阈值内时，补偿器没有输出。而当攻角超出补偿器阈值后，补偿器产生信号修正信号αd。如图3所示，在仿真进行到1.1 s左右时，飞行器攻角超出了补偿器阈值，补偿器产生信号λ2并且补偿信号与αd符号相反。在信号λ2的修正下，控制信号αd幅值降低。控制器再驱动攻角跟踪αd+λ2，攻角就被限制在补偿器阈值附近。

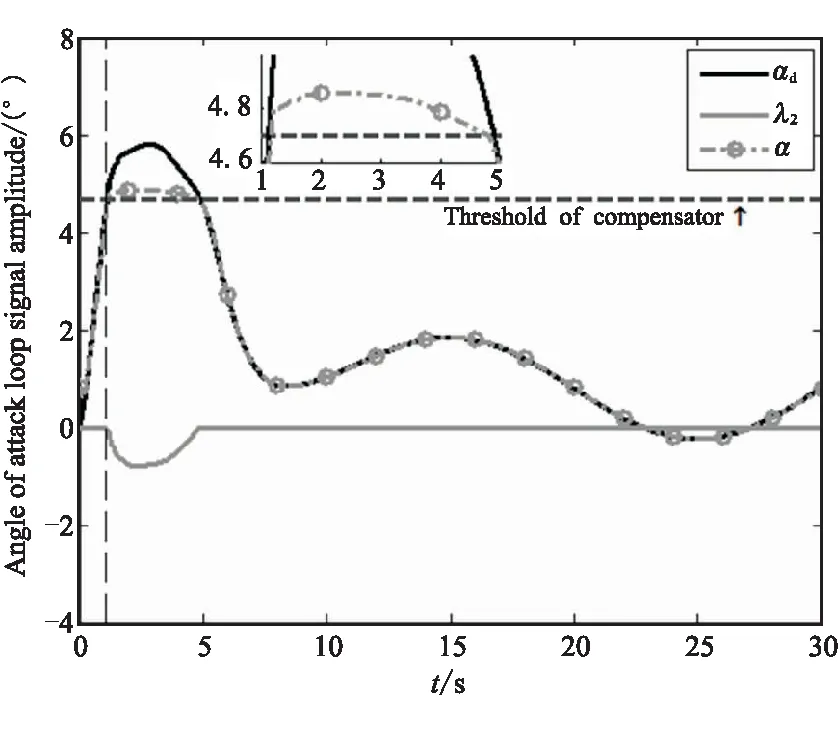
图3 攻角回路控制信号αd和补偿信号λ2Fig.3 Angle of attack loop the control signal αd and compensation signal λ2

这里需要指出的是，补偿器在攻角超出阈值后才产生控制信号，补偿信号可将攻角限制在补偿器阈值附近，但无法避免攻角超出补偿器阈值。因此，补偿器阈值一定要小于期望的攻角边界，且补偿器阈值与攻角边界之间保留一定裕度以保证攻角响应不会超出攻角边界。同样，补偿器对γd和ωd也进行了修正，如图4给出的仿真结果。图5～图7给出了当ωn=0.5时，其它变量的仿真结果。结果表明，这些变量都是有界量，与稳定性分析的结论一致。最后，图7给出控制系统的控制量，其幅值也都在实际物理系统的允许范围内。

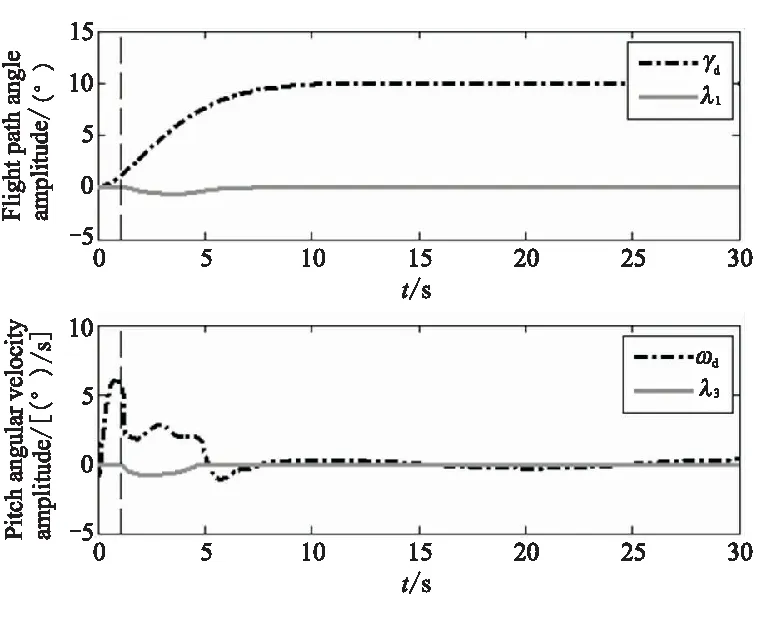
图4 控制信号γd、ωd与补偿信号λ1、λ3Fig.4 Control signals γd，ωd，and the compensation signals λ1，λ3

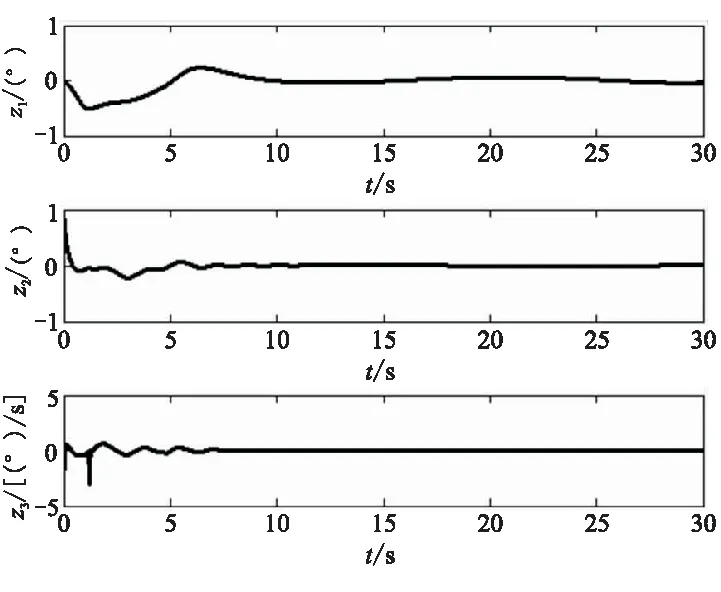
图5 控制误差Fig.5 Tracking errors

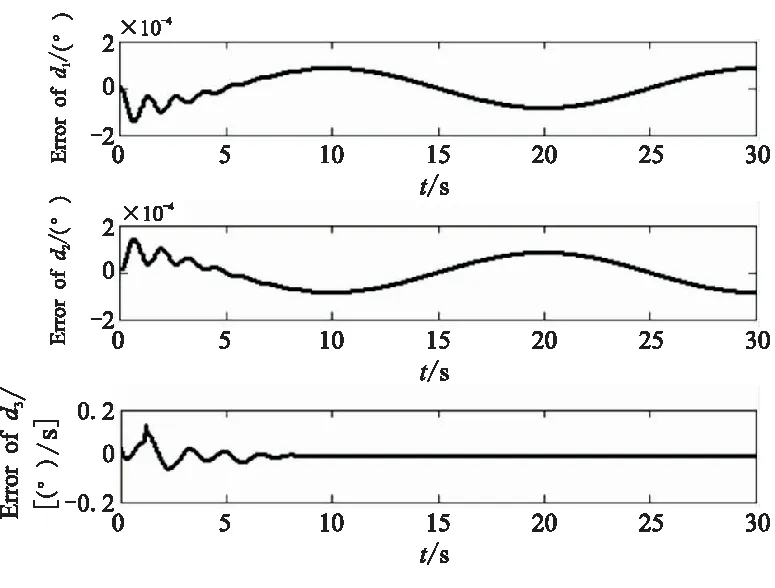
图6 d1、d2和d3估计误差Fig.6 Estimated error of d1，d2 and d3

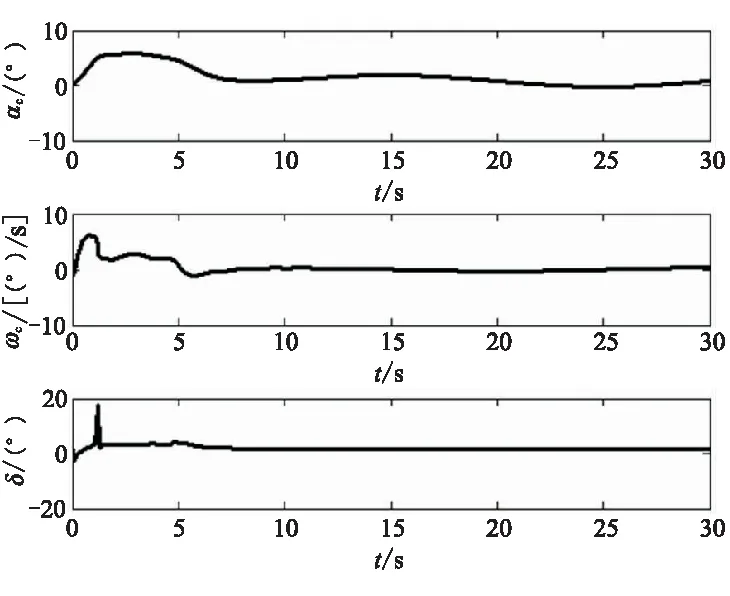
图7 虚拟控制信号及舵偏Fig.7 Virtual controls and elevator

下面选取三组不同的补偿器参数进行仿真实验，通过实验结果对比来说明补偿器参数对闭环响应的影响。补偿器参数的选取在表2中给出。这三组补偿器参数的差别是k4选取了不同的数值。k4是补偿器的输入增益，体现了补偿器对输入信号的放大作用。

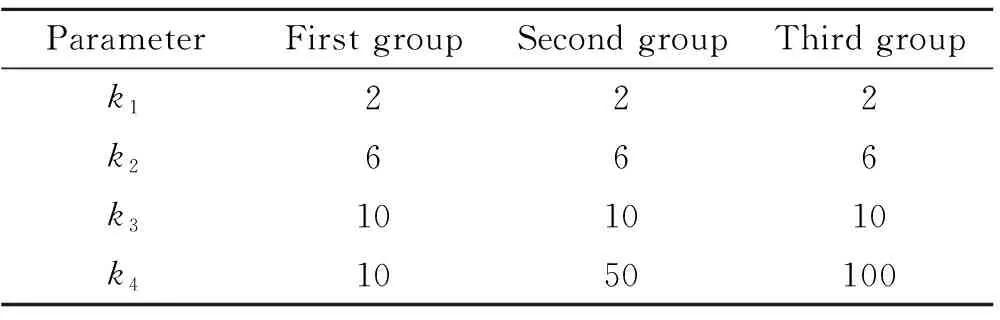
表2 补偿器参数Table 2 Values of compensator parameters

图8是k4取不同值时攻角的响应曲线。当k4=10时，补偿器对攻角的限制作用并不明显，攻角响应超出攻角边界。当k4=50和k4=100时，补偿器对攻角的限制作用明显加强，攻角响应的幅值都被限制在攻角边界以内，且k4增益越大，攻角响应越趋近于补偿器阈值。这说明k4越大，补偿器对攻角的限制作用越好。但k4越大对控制系统执行机构的性能要求越高。图9仿真曲线则表明，随着k4取值的不断增大，舵响应的最大幅值随之变大，且k4过大还会引起执行机构振动。图9中，相比于与k4=50的情况，当k4=100时，在仿真时间1 s附近，舵响应出现了明显的振动。

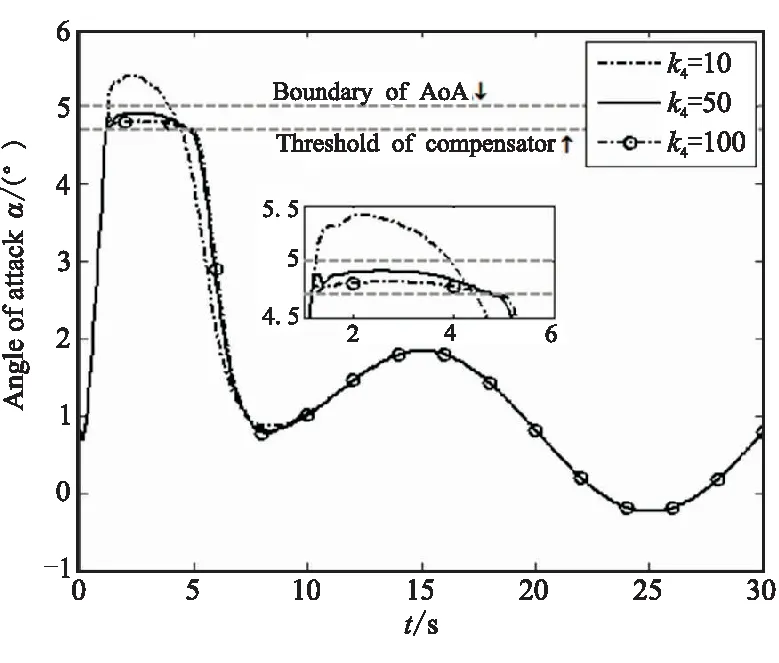
图8 k4取不同值时的攻角响应Fig.8 Angle of attack response of k4 with different values

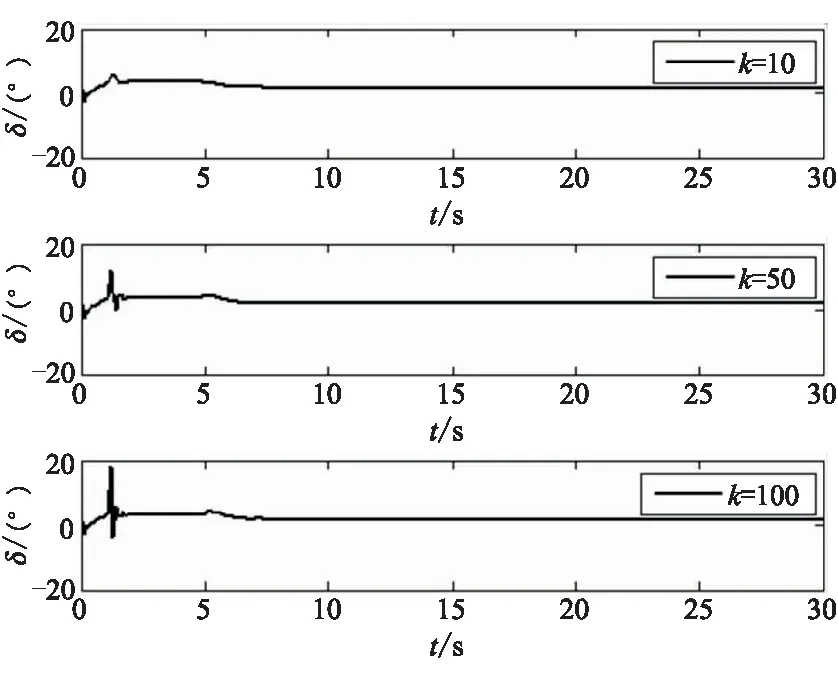
图9 k4取不同值时的舵偏角Fig.9 Deflection of k4 with different values

5 结论

本文针对高超声速飞行器飞行过程中攻角约束问题，提出了一种使用补偿系统限制攻角运动范围的控制方法，并从理论上分析了这种控制器设计方法的稳定性，结果表明：

(1)提出的补偿器限制方法设计简单，能有效控制攻角的运动范围，并且不改变原有反步法控制器收敛精度；

(2)补偿器在攻角超出阈值后，通过对指令的动态修正来实现攻角限制作用，相比于使用障碍Lyapunov函数设计反步法控制器，不需要对虚拟指令进行额外设计，便可达到对状态限制的目的。