大曲酸度值的快速预测模型及方法研究

王开铸，田建平*，孙 婷，鞠 杰，黄 丹，胡新军

（1.四川轻化工大学 机械工程学院，四川 宜宾644000；2.四川轻化工大学 生物工程学院，四川 宜宾644000）

大曲是白酒酿造的糖化剂、发酵剂和生香剂[1-2]。大曲酸度值的形成主要来源于生酸微生物进行的有机酸代谢以及脂肪、淀粉和蛋白质的降解，可作为判断曲香强弱的一个指标[3-5]。酸度值检测的传统方法为电位滴定法，测定过程复杂且耗时长，不能及时地指导培曲生产[6-7]。

目前，相关学者对大曲研究更多是运用相关统计学软件分析大曲不同对象之间的相关性[8-11]，较少运用相关数学模型进行量化分析，存在较大局限性，如：赵金松等[8]运用多元统计、冗余分析（redundancy analysis，RDA）证实了挥发性特征组分与革兰氏阳性（G+）菌量呈显著正相关；王世宽等[9]利用SPSS软件分析得出温度对乳酸菌、酵母菌、霉菌和细菌的变化有较强的相关性；唐贤华等[10]进行窖外模拟发酵试验，通过相关性分析发现糟醅的水分和酸度值与硬度、内聚性、回复性呈显著正相关（P＜0.01），与黏着性呈显著负相关（P＜0.01）；黄治国等[11]研究浓香型酒醅一个发酵周期中主要的微生物群落变化规律和酒醅理化指标的变化规律，表明酒醅细菌群落的多样性与淀粉的相关系数为0.717（P＜0.01），与还原糖的相关系数为0.744（P＜0.01），与总酸的相关系数为-0.704（P＜0.01）。

本研究利用在大曲发酵周期（1～28 d）内采集的大曲内部温度和水分数据，并结合电位滴定法测定的大曲酸度值数据，建立发酵过程中大曲酸度值快速检测的数学模型。首先对原始数据进行异常样本剔除，划分样本集，再分别运用偏最小二乘回归（partial least squares regression，PLSR）、支持向量回归机（support vector regression，SVR）和反向传播神经网络（back propagation neural network，BPNN）建立大曲内部温度、水分与酸度值相关性预测模型，运用决定系数与均方根误差（root mean square error，RMSE）对训练集、测试集进行效果评价，找出最佳数学模型，并采用外部验证方式验证模型效果，为大曲指标的快速检测技术提供依据，对于大曲生产技术进步和产品质量升级具有重大现实意义。

1 材料与方法

1.1 材料与试剂

浓香型大曲：四川宜宾某酒业有限公司；氢氧化钠（分析纯）：成都市科龙化工试剂厂。

1.2 仪器与设备

PT100温度传感器：杭州美控自动化技术有限公司；FDS-100土壤水分传感器：邯郸市丛台锐达仪器设备有限公司；曲房监测系统：四川轻化工大学自制；CP214电子天平、STARTER 3100 pH计：奥豪斯仪器（上海）有限公司；78-HW-1恒温磁力搅拌器：金坛市医疗器械厂；ZDJ-5B型自动滴定仪：广州市深华生物技术有限公司。

1.3 实验方法

1.3.1 数据的采集与检测

利用曲房监测系统采集浓香型大曲的内部温度和水分，培曲前13 d每天从两间曲房分别采集4个不同浓香型大曲样本，后15 d隔天采集，共160个样本，另外再采集11个样本（发酵时间为1 d、3 d、5 d、7 d、9 d、11 d、13 d、17 d、21 d、25 d、28 d）作为外部验证预测不参与建模，取样点见图1，并运用电位滴定法[12]检测监测点大曲样本的酸度值。

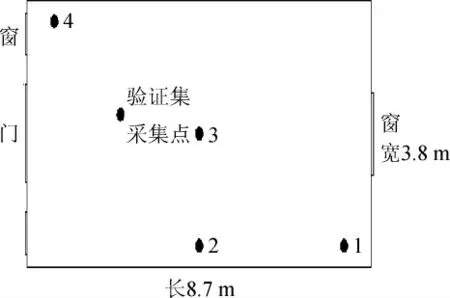
图1 大曲取样点分布Fig. 1 Distribution of sampling points of Daqu

1.3.2 数据分析方法

（1）样本集划分

为了达到充分训练模型的效果，训练集样本数据要最大程度体现所有样本数据状况，根据K-S算法[13-15]将文中160个样本数据按照3∶1的比例划分为120个训练集样本，40个测试集样本。

（2）偏最小二乘回归[16-17]

偏最小二乘回归（PLSR）是一种新型的多元统计数据分析方法，它将多元线性回归分析、主成分分析与典型相关分析有机结合起来，其建模原理也是建立在这3种分析方法之上的，通过从自变量集合中提取若干相互独立的主成分来建立与因变量之间的关系。

具体建模方法：设有2个自变量X=（x1，x2）、1个因变量Y=（y1）和n个样本点，其中x1为大曲温度，x2为水分，y1为大曲酸度，分别在X和Y中提取出主成分分量t1和u1，要求t1和u1应尽可能大地携带各自数据表中的变异信息，以及t1和u1的相关程度能够达到最大，在第一个主成分分量t1和u1被提取后，分别实施X对t1以及Y对u1的回归。若回归方程此时已经达到满意的精度，则成分确定，否则将利用X被t1以及Y被u1解释后的残余信息进行第二轮的成分提取，如此往复，直到精度满足要求为止。

（3）支持向量回归机

支持向量回归机（SVR）是一种监督学习方法，广泛应用于分类和回归问题，其是由VAPNIK V N[18]在基于统计学理论中结构风险最小化原理的基础上提出的。SVR最先是用来解决分类问题，后来通过使用替代惩罚函数（loss function）来解决回归问题[19-22]。

大曲发酵酸度值预测模型样本集合为{（xi，yi），…，（xs，ys）}，i=1，2…，s，其中xi=（Xi1，Xi2）为大曲酸度值预测模型的特征矩阵，s=120，Xi1为大曲温度，Xi2为大曲水分，yi为大曲发酵酸度值，通过求解函数f（x）来预测大曲温度、水分对应大曲发酵酸度值y值。

线性函数设为式（1）：

式中：f（x）为大曲发酵酸度值预测模型输出，ω、b为大曲发酵酸度值预测模型系数。

引入松弛变量ξi、ξ*i，可将支持向量机线性回归求解问题转化为优化问题的方式确定ω的值。

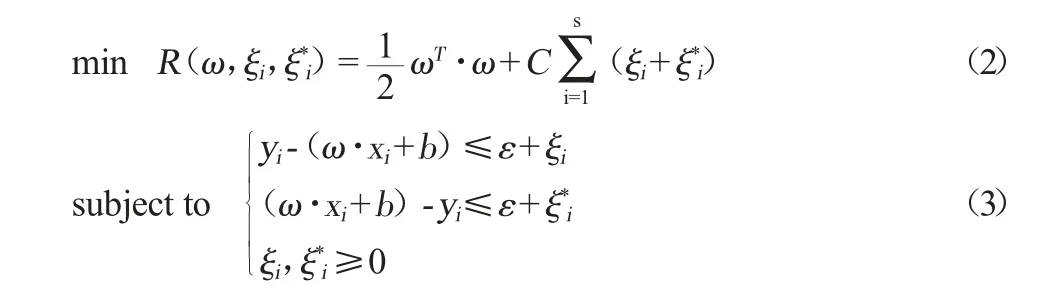
式中：yi为大曲发酵酸度值预测样本数据的输出，xi为大曲发酵酸度值预测样本数据的输入，ε为松弛因子，C（C＞0且为常数）为惩罚因子。

在实际工作中，采用上述线性回归方法，难以达到大曲发酵酸度值预测的精度要求，因此引入Lagrange对偶问题求解，得到式（4）。

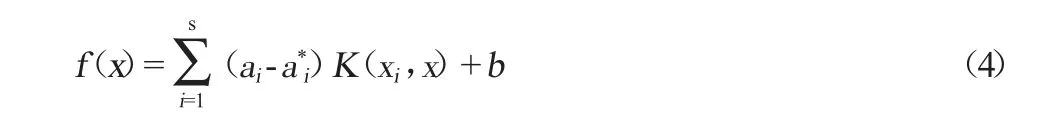
式中：σ为高斯核宽度系数。

（4）BP神经网络[23]

BP神经网络（BPNN），即误差反向传播算法的学习过程，包括信息的正向传播和误差的反向传播两个过程。一般结构可分为输入层、隐含层、输出层。在输入层输入训练集样本，训练集样本乘各自的连接权值输入到隐含层，隐含层将上层传递下来的值再乘相应的连接权值输入给输出层，输出层根据期盼结果判断神经网络处理是否正确，若正确则增加相应的连接权值，相反，则减少相应的权值。神经元的输出大曲酸度值yi可以表示为式（6）。

式中：xi（i=1，2，…，n）为当前神经元相连的其他神经元传递的输入信号，即xi=（X1，X2），X1为大曲温度，X2为水分，wij为从神经元j到神经元i的连接强度或权值，θi为神经元的激活阈值或偏置，f为激活函数或转移函数神经元的输出。

（5）模型评价方法

为了验证3种算法得到模型的泛化能力和预测精度，采用决定系数R2与均方根误差（RMSE）2个指标进行评价，指标计算公式分别见式（7）和式（8）。在样本数据相同的前提下，R2越接近1，RMSE越接近0时，模型的预测能力越强[24]。

式中：n为训练集样本总数；m为验证集样本总数；yˆi为第i个样本的预测值；yi为第i个样本的实际测量值；ym为所有样本实际测量值的平均值。

2 结果与分析

2.1 数据结果分析

一个发酵周期（28 d）不同样本大曲内部温度、水分和酸度值随时间变化的曲线见图2。

由图2a可知，大曲内部温度变化呈现先上升后逐渐保持稳定，再到缓慢下降的趋势。前3天温度迅速增长，可能是由于大曲内部水分含量高，发酵前期微生物富集较快，第6天对曲房进行第一次翻曲（收堆），引起温度小幅下降，第18天进行第二次翻曲（并房），导致温度小幅上升。由图2b可知，大曲内部水分在整个发酵周期里呈现下降趋势，前13天水分急剧下降，可能是由于霉菌等微生物大量生长繁殖产热，大曲水分被蒸发和消耗，而在发酵后期水分呈缓慢下降趋势，可能是温度降低水分蒸发变慢。由图2c可知，酸度值在整个发酵周期呈下降趋势。前8天酸度值急剧下降，分析可能是产酸细菌大量繁殖，温度迅速上升，产酸量增幅较大；发酵8～15 d酸度值下降趋势稍缓，产酸细菌生长较稳定，产酸量增幅较小；发酵后期，酸度值趋于平缓，表明产酸细菌生长受阻，此时，大量的霉菌和酵母菌开始生长，产酸细菌则停止代谢。分析表明，大曲内部温度、水分与酸度值相关性无法直接获得，需要借助现代数学方法建立相关预测模型，解析大曲内部温度、水分与酸度值之间的关系。

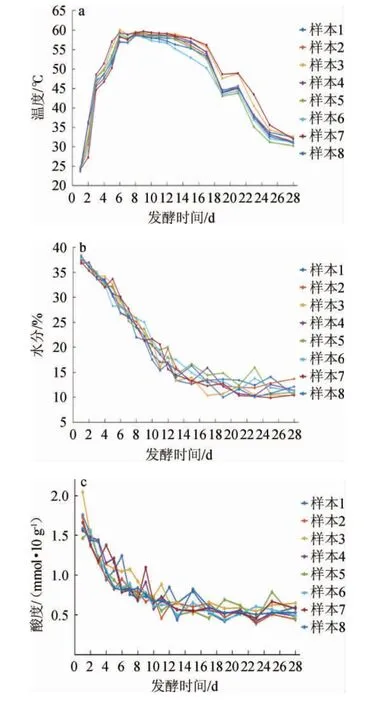
图2 发酵过程中大曲内部温度（a）、水分（b）和酸度值（c）的变化Fig. 2 Changes in temperature (a), moisture (b) and acidity value (c)of Daqu during fermentation

2.2 酸度值预测模型的建立

2.2.1 PLSR法建立的大曲酸度值预测模型

PLSR法建立大曲酸度值预测模型的预测值与实测值的相关性散点分布见图3。

采用PLSR法所建模型，在训练集与测试集上的决定系数R2、均方根误差（RMSE）分别为0.796 9和0.784 7、0.159 0和0.137 2。由图3可知，训练集与测试集的数据都偏离直线的数据点较多，故PLSR建立大曲酸度值预测模型性能很差，模型只能够做近似运算。

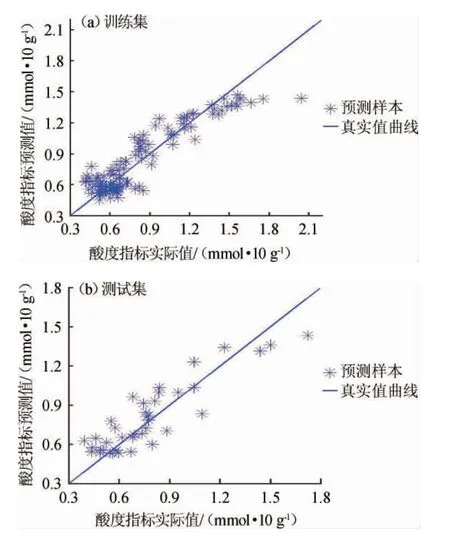
图3 偏最小二乘回归法大曲酸度值预测值与实测值的相关性Fig. 3 Correlation between the measured value and predicted value of Daqu acidity value by partial least square regression method

2.2.2 SVR法建立的大曲酸度值预测模型

SVR法建立大曲酸度值预测模型预测值与实测值的相关性散点分布见图4。

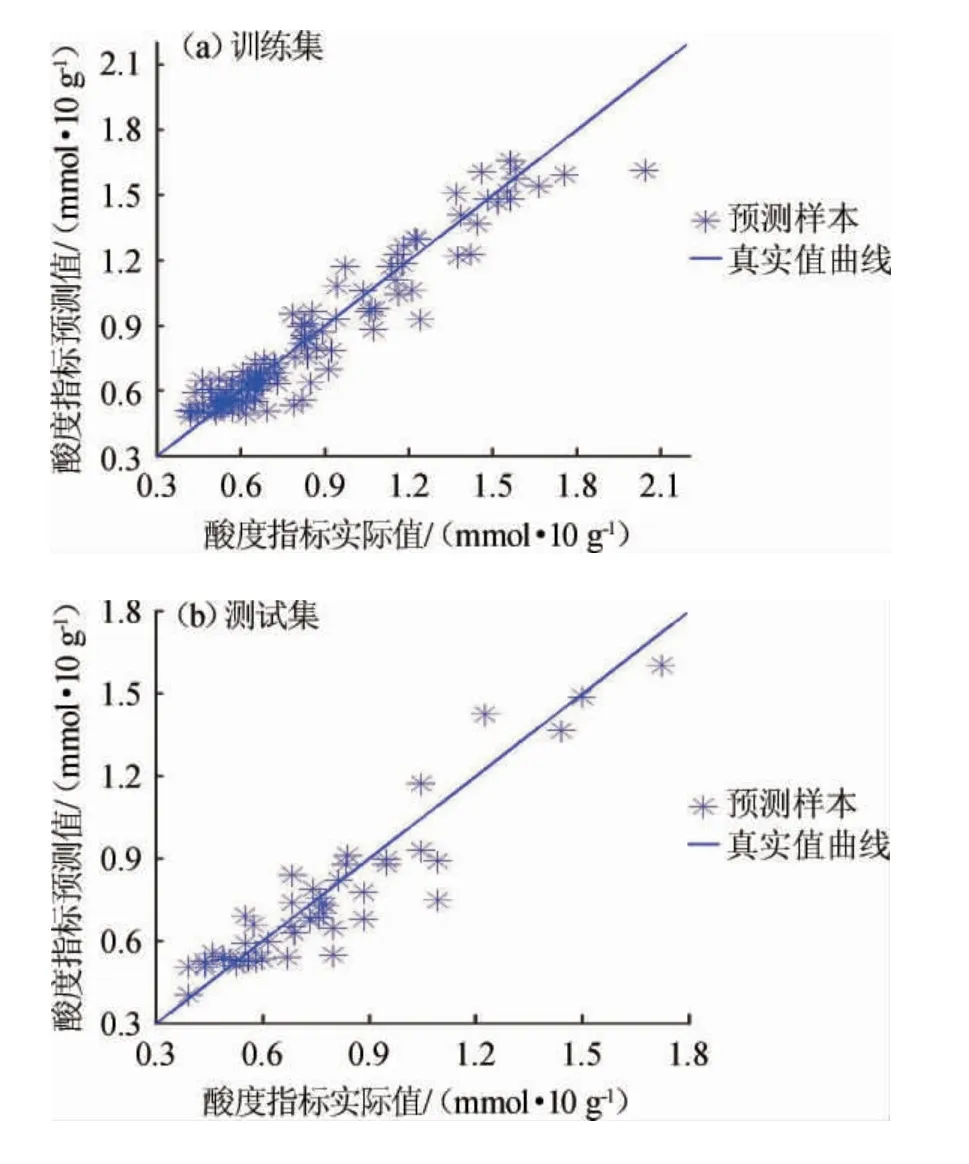
图4 支持向量回归机法大曲酸度值预测值与实测值的相关性Fig. 4 Correlation between the measured value and predicted value of Daqu acidity value by support vector regression machine method

采用SVR法所建模型，在训练集与测试集上的决定系数R2、均方根误差（RMSE）分别为0.916 7和0.896 7、0.101 8和0.101 0。由图4可知，训练集与测试集的数据都较好的集中于直线两侧，故模型性能良好，但样本数据在训练集数据上的表现要比测试集上好，说明模型的泛化性能不好，抗干扰能力较差。

2.2.3 BPNN法建立的大曲酸度值预测模型

BPNN法建立大曲酸度值预测模型的预测值与实测值的相关性散点分布见图5。

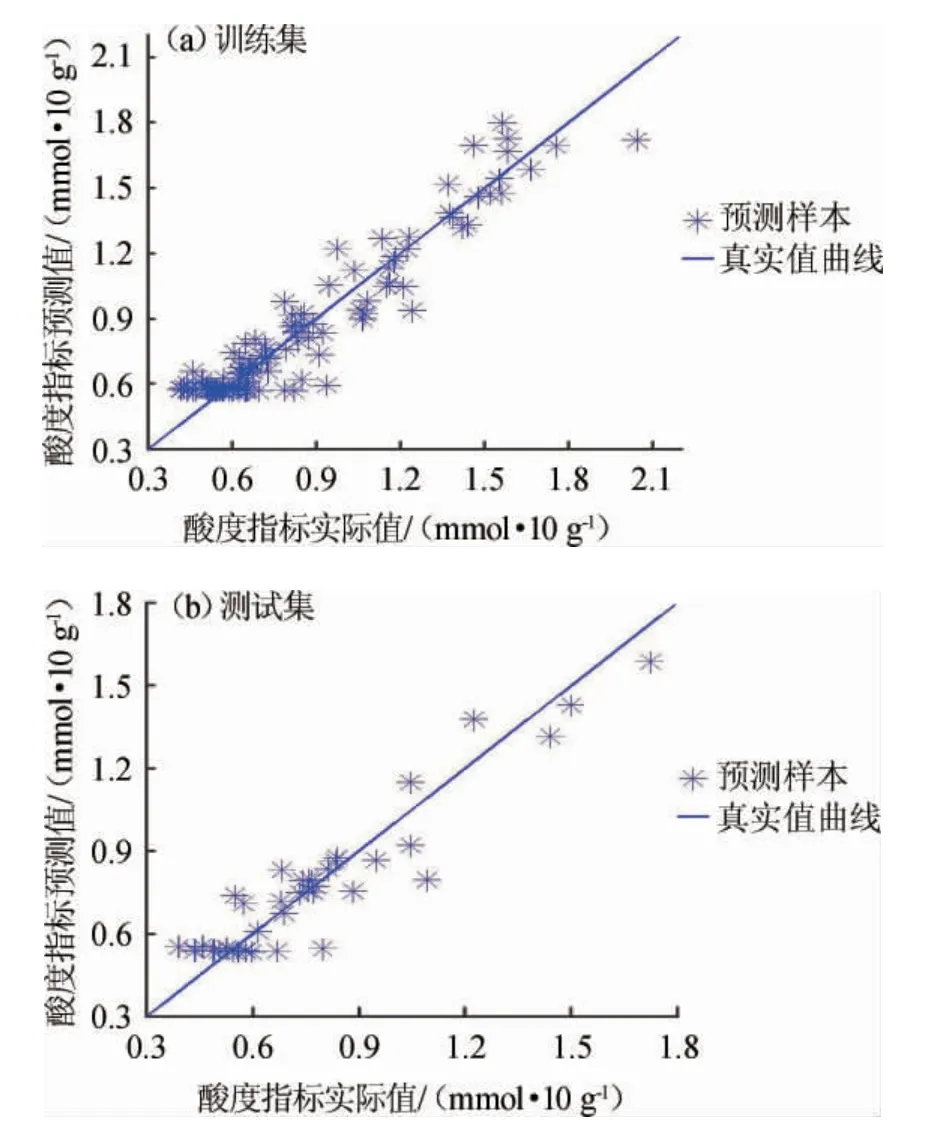
图5 BP神经网络法大曲酸度值预测值与实测值的相关性Fig. 5 Correlation between the measured value and predicted value of Daqu acidity value by BP neural network method

采用BPNN法所建模型，在训练集与测试集上的决定系数R2、均方根误差（RMSE）分别为0.901 3和0.874 5、0.110 8和0.104 8。由图5可知，训练集与测试集的数据都较好的分布于直线两侧，故模型性能良好，但测试集效果明显不如SVR法的测试集效果且比PLSR法的测试集效果好，同SVR模型一样模型的泛化性能不好，抗干扰能力较差。

2.2.4 预测模型的效果对比

由图6可知，采用PLSR法建立的大曲酸度值预测模型不管是在训练集还是在测试集上性能都较差，而SVR、BPNN法建立的两种大曲酸度值预测模型的精度均较高，模型的均方根误差均较小，这表明本研究选取2个参数大曲内部温度、水分所建立的预测模型可以成功地对大曲酸度值进行预测。此外，采用SVR法建立的大曲酸度值预测模型在训练集和预测集的决定系数与均方根误差都比BPNN好且运算时间更短，故采用SVR法建立的大曲酸度值预测模型性能要稍优于BPNN法建立的大曲酸度值预测模型，具有更好的实用性。SVR模型具有更强大的非线性拟合能力，因而具有较强的优越性。

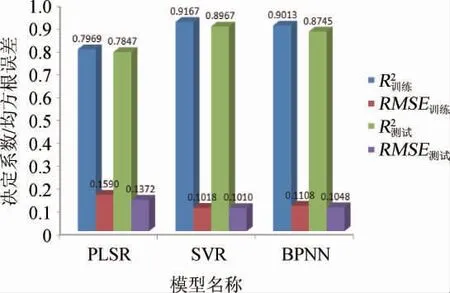
图6 三种算法预测结果对比Fig. 6 Comparison of prediction results of three algorithms

2.3 模型外部验证

为了进一步验证模型的准确性和稳定性，采用外部验证方式验证模型效果，即将未参与建模的11个预测样本组成的验证集代入模型进行预测，同时与电位滴定法测得的真实值进行比较，对比结果见表1。由表1知，酸度值实际值和预测值都呈下降的趋势，且模型验证集的大曲酸度值结果与电位滴定法测得的真实值相比，最小相对误差为1.6%，最大相对误差为11.1%。

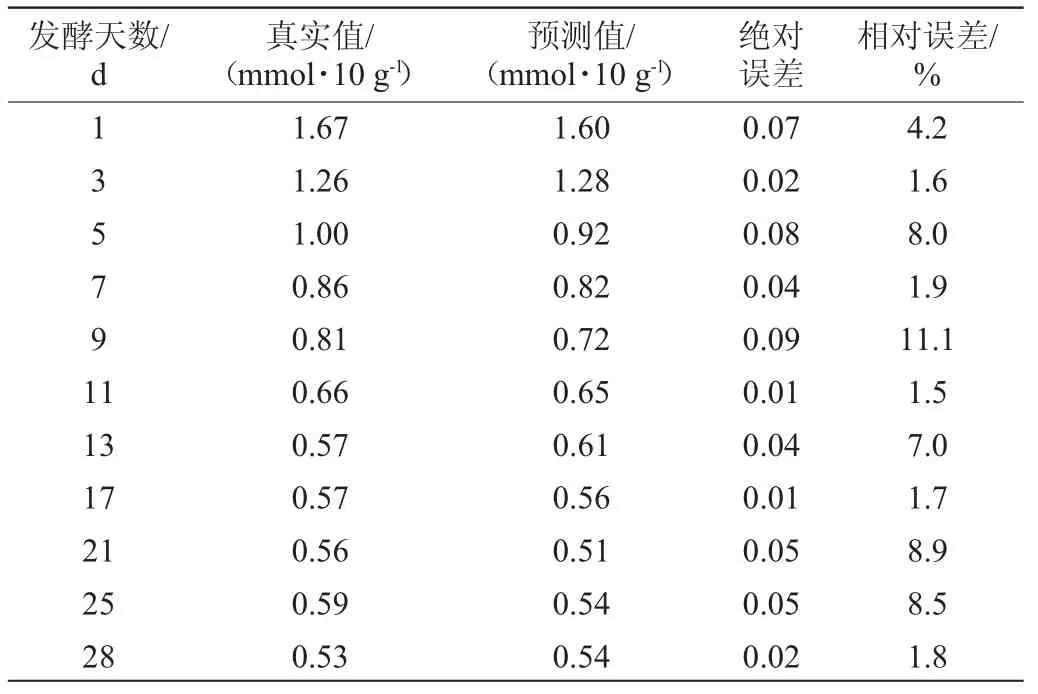
表1 酸度真实值与预测值结果对比Table 1 Comparison of actual acidity and predicted results

3 结论

大曲发酵过程中的酸度值与大曲内部温度、水分相关性无法直接获取，必须借助现代数学方法进行分析。分别使用偏最小二乘回归（PLSR）、支持向量回归机（SVR）、BP神经网络（BPNN）建立大曲内部温度、水分与酸度值的关联性预测模型，综合评价指标显示支持向量回归机（SVR）所建大曲酸度值预测模型效果最好，测试集上的决定系数（R2）为0.874 5，均方根误差（RMSE）为0.104 8。该模型经外部验证后，模型酸度的预测值与实际值的相对误差为1.6%～11.1%，可以通过检测大曲内部温度、水分直接预测出大曲酸度值。本研究通过对大曲发酵过程酸度值的实时、无损检测，为所有种类大曲酸度值的检测提供了新方法，为其他理化指标的实时、无损检测提供了新思路，为大曲在线检测与控制系统的开发提供了理论支撑。