涡流脉冲热像技术中基于神经网络的检出/漏检预测研究

孙吉伟,孙 浩,谢 敏,李泓江,邓栋栋,曹 涛

(中国华阴兵器试验中心，陕西 华阴 714200)

0 引言

主动红外热像技术，是一种采用主动式受控激励源来激发被测对象的温度场分布，通过红外热像仪采集得到图像，从而识别被测对象中缺陷的无损检测技术[1-2]，具有检测效率高、操作简单、成像效果直观等优势[3-4]。西安科技研究院的LI Y.[5]提出了一种研究冲击复合材料层合板的损伤演化的新方法，通过主动红外热像技术获得不同疲劳循环实验下的图像，并做增强处理，最后获得了疲劳周期与损伤面积之间的关系。哈尔滨工业大学的TANG Q.[6]提出了用于脉冲热像技术的Markov-PCA-BP算法，实现了圆孔缺陷深度及直径的预测。默罕默德大学的Ahmed Kabour[7]提出了一种基于红外热像分析材料表面缺陷特征的方法，采用小波变换多分辨率的形式提取图像的特征，有效地实现了亚表面缺陷的检测。日利纳大学的 Zuzana Stankovičová[8]介绍了超声红外锁相热像技术用于金属部件的检测，通过相位图的处理实现了3～5μm微小缺陷的检测。

在采用主动红外热像进行检测的过程中，由于检测系统的变化、环境的干扰、人工操作的误差等因素必然会影响检测的结果。为评价主动红外热像技术检测结果的可靠性，装甲兵工程学院的ZHU J.Z.[9]提出了用于超声红外热像技术的检出概率研究方法，通过对含有疲劳裂纹的金属平板试件进行检测实验，绘制了检出概率曲线并给出了Wald 置信区间，MIN Q.X.等人[10]根据检出概率理论实现了超声锁相热像技术中检测条件的优化选择。哈尔滨工业大学的LIU J.[11]采用光激励锁相技术对碳纤维材料进行检测，完成了不同检出阈值和不同调制频率下的实验结果分析。针对涡流脉冲热像技术的检出概率研究，英国无损检测中心的Ben Weekes[12]对钢、钛、镍基合金3 种材料中的疲劳裂纹进行检测，并将实验数据输入到累积正态分布模型中，得出的a90,95(检出概率为90%、置信度为95%时，疲劳裂纹对应的长度)分别为0.60 mm，0.78 mm 和1.50 mm。

目前大多学者停留在单一检测条件下的不同尺寸裂纹检出概率的研究上，同时检出概率实验的数据较少[13]，并且目前的检出概率研究大多停留在检出概率曲线的绘制阶段。然而，在检出概率的研究中，为获得更详细具体的检出概率曲线需要大量的实验数据作为支撑，此外对于实际的涡流脉冲热像检测中，检出/漏检[14](hit/miss)则是衡量检测结果的重要标准。为达到节约实验成本并完成hit/miss研究的目的，本文提出了一种基于 BP(back propagation)神经网络的检出/漏检预测方法。首先，制作了30 组含有不同尺寸疲劳裂纹的金属试件，并完成了15 组不同检测条件下的裂纹检测实验。其次，分别绘制了3 组检出概率曲线，并完成了不同检测条件对检出概率的影响分析。最后，为实现检出/漏检的可靠性预测，构建了基于BP 神经网络的检出/漏检预测模型，并以50 组数据为样本进行测试，实现了不同检测条件下不同尺寸裂纹的检出/漏检0 误差预测。

1 实验装置及试件

图1所示为本课题组的涡流脉冲热像技术实验台，由型号为FILR-T640(640 pixelX480 pixel 的像素，30 Hz 的采样频率，0.035℃的热灵敏度)的红外热像仪、功率为3 kW 的激励电源、水冷装置、矩形线圈、采集终端以及三自由度的移动平台组成。

图1 涡流脉冲热像实验台示意图Fig.1 Schematic diagram of ECPT system

通过对大量装甲装备典型结构件的统计发现，在金属结构件拐角等应力集中区域存在严重的贯穿裂纹。为此，本文以C45 为原材料，通过疲劳拉伸实验获得了如图2所示的贯穿裂纹，并按照虚线进行线切割，获得了如图2中a，b 所示尺寸为240 mm X5 mmX47.4 mm 的试件。本文以30 组含有不同尺寸的疲劳裂纹试件为研究对象，其编号和尺寸如表1所示。

图2 含疲劳裂纹的45 钢平板试件Fig.2 C45 flat specimen with fatigue crack

2 热响应信号提取

2.1 实验方案设计

在涡流脉冲热像技术中，激励时间、激励强度(系统功率的百分比)和提离距离(电磁线圈下表面与试件上表面的距离)是影响裂纹热响应信号的重要检测条件，为了能更准确地分析不同检测条件对检出概率的影响，分别在这3 个检测条件中选定5个梯度，设计了如表2所示的实验方案，在特定检测条件下的实验进行3 次以消除偶然误差(共计1350 组)，提高实验数据的可靠性。为方便下文对实验数据的描述与分析，对不同检测条件采用如下形式进行表示:激励时间-激励强度-提离距离，如100-60-10表示激励时间为100 ms、激励强度为60%、提离距离为10 mm 的检测条件。

表1 裂纹长度及其编号Table 1 Crack lengths and numbers

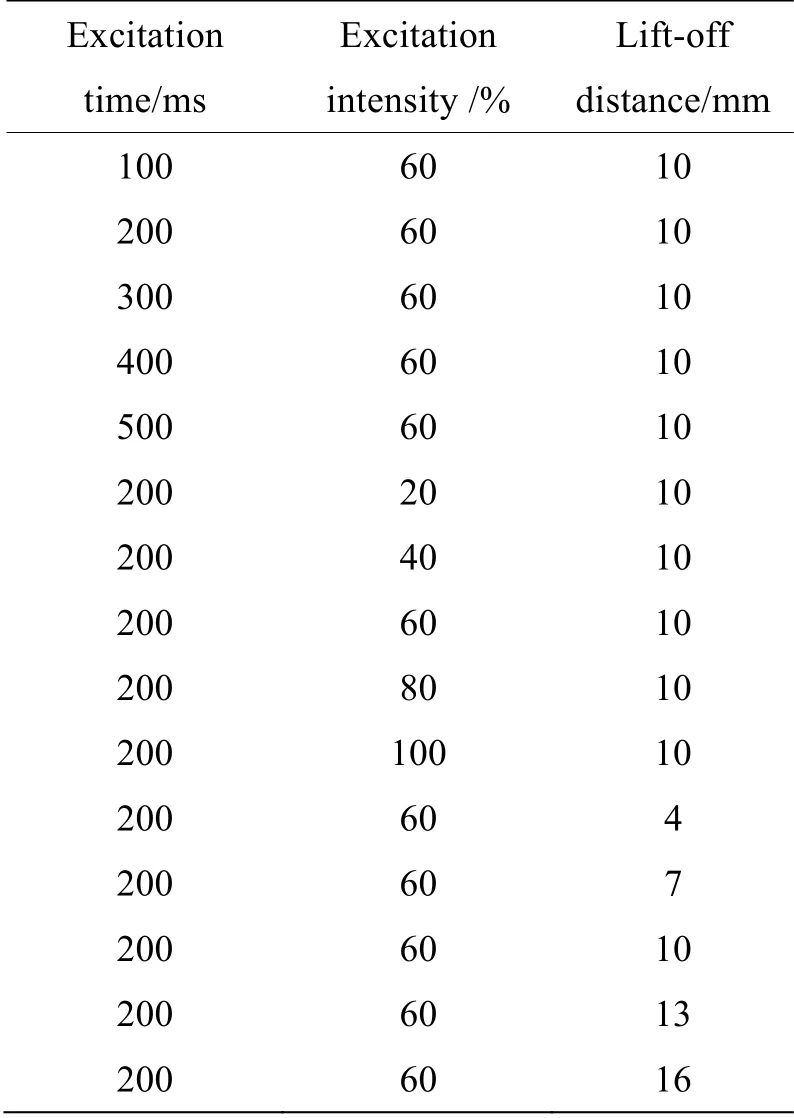
表2 实验主要参数Table 2 Main parameters of test

2.2 热响应信号计算理论

通常，在涡流脉冲热像检测中将激励结束时刻裂纹区域的平均温升作为热响应信号，即:

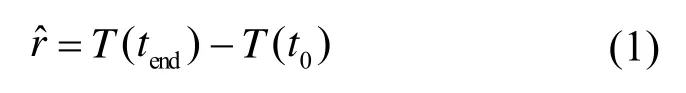
式中:t0、tend分别表示激励开始的时刻和激励结束的时刻。

随机选取的编号为S10 的试件，在检测条件200-60-10 下的热像图如图3所示，其中(a)，(b)分别为激励开始时刻和激励结束时刻的裂纹生热效果图。图中所示的框线区域为裂纹区域，取裂纹区域的平均值根据式(1)即可完成对热响应信号的计算。

图3 裂纹区域热像图Fig.3 Thermal image of a crack region

最适合分析"hit/miss"形式数据的数学模型是Logistic 回归模型，在"hit/miss"形式的数据中，通过记录1(或0)来表示缺陷检出(漏检)，其概率密度函数服从二项分布，并采用y标记检测事件，其中y=1 表示缺陷检出，y=0 表示缺陷漏检。检出概率函数POD(a)可表示为:

式中:a为缺陷的尺寸;α为拟合随机项;β为拟合后缺陷尺寸的系数。对式(2)进行Logit 变换，可得:

将第k次检测时缺陷被检出的概率标记为pk，即POD(yk=1)=pk，将缺陷漏检的概率标记为1-pk，即POD(yk=0)=1-pk。那么，缺陷检出概率的联合概率密度函数可表示为:

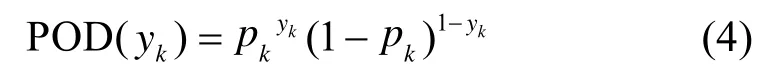
构造似然函数可表示为:

式中:n表示检测次数。

对式(5)的似然函数取自然对数可得:

通过极大似然估计即可求出α，β的估计值，，进而求出检出概率的值。

3 检出概率曲线分析

检出概率曲线是特定检测条件下，不同裂纹尺寸检出概率的最直观反映。实际检测中涡流脉冲热像检测技术的检测能力可通过检出概率值90%时的裂纹尺寸具体表现。本章的检出概率计算中，检出阈值设定为1.5℃(通常检出阈值为背景噪声的2倍)，根据前期的研究成果，采用式(2)对检出概率进行计算，分别估算出如表3、4、5 所示的不同检测条件下的检出概率模型参数，并绘制了如图4、5、6 所示的检出概率曲线。

通过图4中不同激励时间下检出概率曲线的对比，可以看出:在涡流脉冲热像检测中，激励强度和提离距离保持不变时，对于同一尺寸裂纹，激励时间越长，检出概率越高;对于同一激励时间，裂纹尺寸越大，检出概率越高;可以通过增加激励时间来提高检测能力。通过表3中检出概率模型参数估计值的对比，可以看出:在涡流脉冲热像检测中，对于相同激励强度和提离距离的检测，激励时间越长，、a50,a90(检出概率为50%、90%时对应的裂纹长度)值越小，即与图4分析得到激励时间越长检测能力越强的结论相一致;随着检测能力的提高，检测数据的标准差具有逐渐降低的趋势。需要说明的是，在实际实验中，环境等误差不可避免，因此，在与激励时间为200 ms 时相比，激励时间为300 ms 时的标准差略微增大，但是，整体呈现出逐渐降低趋势。

通过对图5不同激励强度下的检出概率曲线的比较，可以得到:激励时间和提离距离保持不变时，激励强度越高，检出概率越高;对于同一激励强度，裂纹尺寸越大，检出概率越高;可以通过增加激励强度来提高检测能力。通过表4中检出概率模型参数估计值的对比，可以看出:在涡流脉冲热像检测中，对于相同激励时间和提离距离的检测，激励强度越大，、a50,a90值越小，即与图5分析得到激励强度检测能力越强的结论相一致;随着激励强度的提高，检测数据的标准差逐渐降低，数据的波动性更小。

表3 不同激励时间条件下的检出概率模型估计值Table 3 Estimation of POD model parameters under different excitation time

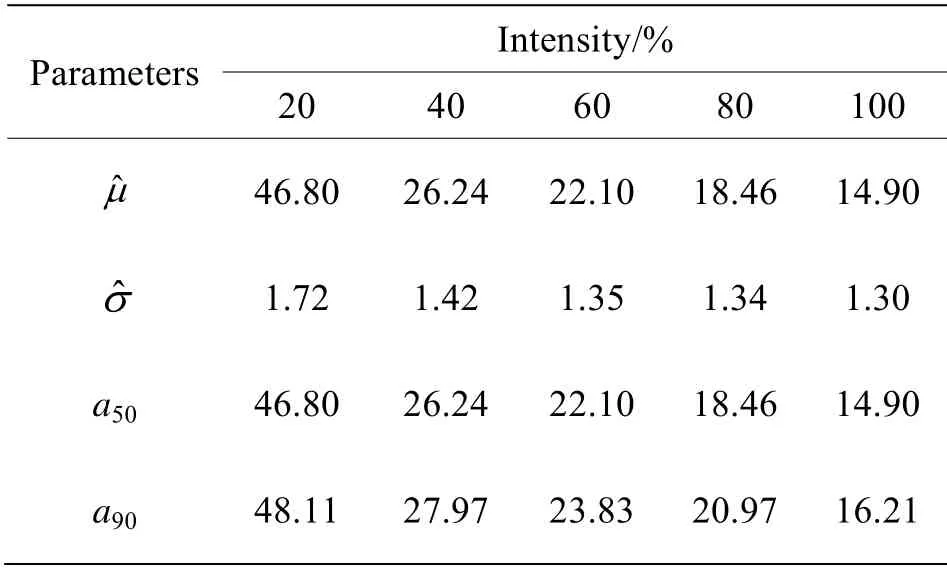
表4 不同激励强度条件下的检出概率模型估计值Table 4 Estimation of POD model parameters under different excitation intensity

表5 不同提离距离条件下的检出概率模型估计值Table 5 Estimation of POD model parameters under different lift-off distance

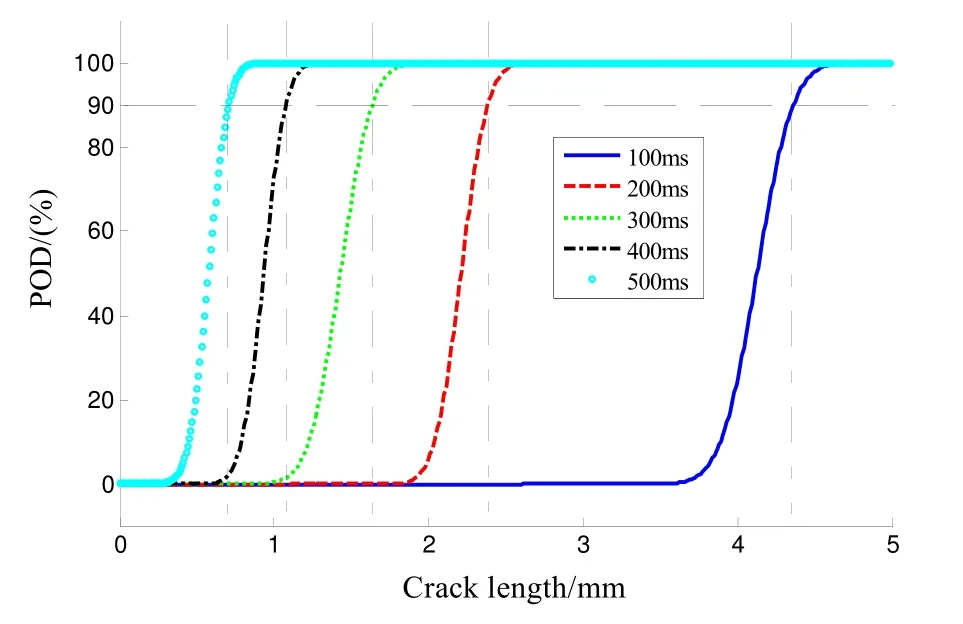
图4 不同激励时间下的检出概率曲线Fig.4 POD curves under different excitation time

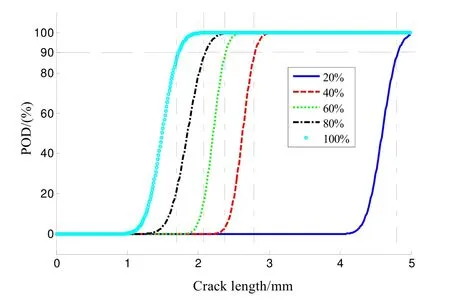
图5 不同激励强度下的检出概率曲线Fig.5 POD curves under different excitation intensity

通过对图6不同提离距离下的检出概率曲线的比较，可以得出:激励时间和激励强度保持不变时，对于同一尺寸裂纹，在4 mm、7 mm、10 mm、13 mm、和16 mm 五个提离距离下，在提离距离等于10 mm时，检出概率最高;对于同一提离距离，裂纹尺寸越大，检出概率越高;可以通过调整适当的提离距离来提高检测能力。通过表5中检出概率模型参数估计值的对比，可以看出:在涡流脉冲热像检测中，激励时间、激励强度保持不变时，在4 mm、7 mm、10 mm、13 mm、和16 mm 五个提离距离下，提离距离等于10 mm 时，、a50、a90值最小，即与图6分析得到在提离距离等于10 mm 时，检测能力最强的结论相一致;随着检测能力的提高，检测数据的标准差具有逐渐降低的趋势。

4 检出/漏检预测

在涡流脉冲热像检测中，检出概率曲线是指导工程应用的重要理论基础。目前，检出概率曲线只能针对特定的、单一的检测条件。然而，在实际检测时，必须考虑多个检测条件的共同影响，由此，单一检测条件下的检出概率曲线无法满足检测的需求。同时，为解决工业检测现场设备用户提出的特定检测条件下，特定尺寸的缺陷能否被检测出的问题，本文引入了BP 神经网络[15]，将不同检测条件下的检出概率进行整合，构建了基于BP 神经网络的检测结果(检出/漏检)预测模型。

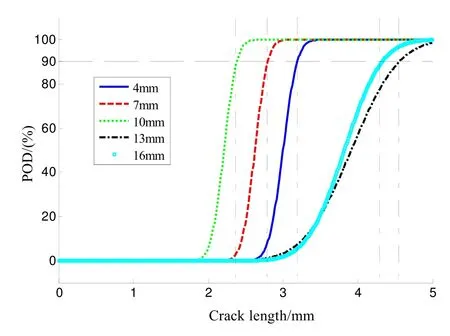
图6 不同提离距离下的检出概率曲线Fig.6 POD curves under different lift-off distance

具体地，采用 PODBP0/1～(a,T,I,L)表示BP 检出预测模型，其中a，T，I，L分别表示被测试件含有的裂纹尺寸、激励时间、激励强度以及提离距离。将前期得到的1350 组数据根据0.8℃的阈值转换成1/0 形式的hit/miss 数据。将实验数据随机分成1300组训练样本和50 组测试样本，将裂纹尺寸、激励时间、激励强度、提离距离这4 组特征作为网络的输入，即该BP 神经网络具有4 个输入层神经元;输出结果只有两种形式检出/漏检，即输出层节点个数为1 个(取值为0 或1);隐含层节点数为4;最大训练次数为1000;训练步长为10;学习率为0.6;目标误差为0.02。在采用BP 神经网络进行仿真训练的过程中，通过newff 实现网络的建立，并通过train 进行网络的训练，最后采用sim 函数完成网络的仿真测试。

图7所示为BP 神经网络误差曲线曲线，经过165 次训练后达到目标误差。在50 个测试样本中，含缺陷的数据37 组，不含缺陷的数据有13 组，经过BP 神经网络预测检测准确率为100%，误差为0。可以看出:本文建立的BP 神经网络的hit/miss 模型可实现不同检测条件下的检出/漏检预测。

5 结论

针对涡流脉冲热像检测中设备用户存在的疑问，本文提出了一种针对不同检测条件下不同裂纹尺寸的检出/漏检预测方法，得出的结论如下:

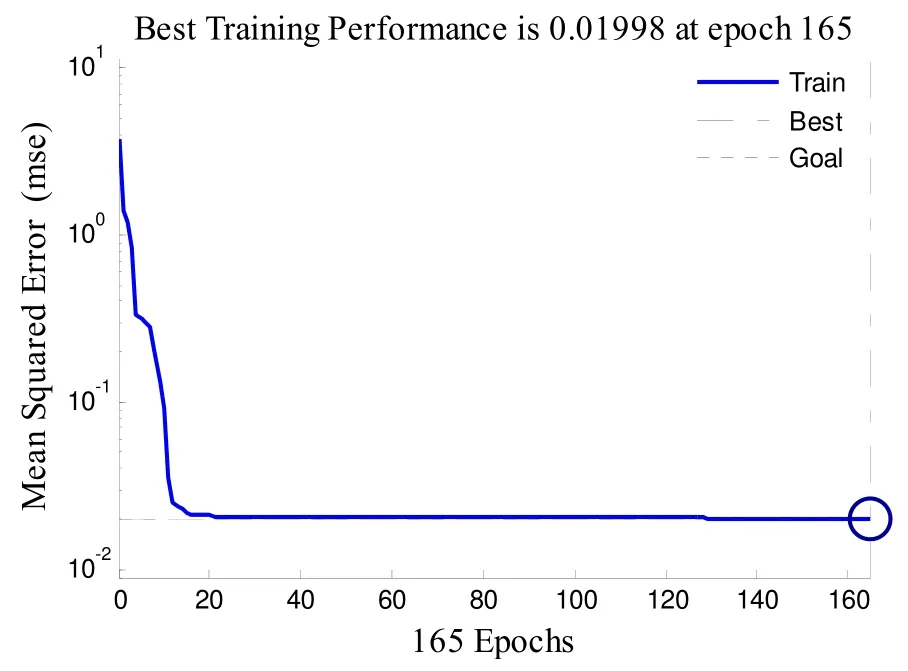
图7 BP 神经网络收敛曲线Fig.7 Convergence of training with BPNN

1)在涡流脉冲热像检测中，对于同一尺寸裂纹，激励时间越长，检出概率越高;对于同一激励时间，裂纹尺寸越大，检出概率越高;可以通过增加激励时间来提高检测能力。

2)对于同一尺寸裂纹，激励强度越高，检出概率越高;对于同一激励强度，裂纹尺寸越大，检出概率越高;可以通过增加激励强度来提高检测能力。

3)对于同一尺寸裂纹，在激励强度60%的条件下，提离距离等于10 mm 时，检出概率最高;对于同一提离距离，裂纹尺寸越大，检出概率越高;可以通过调整适当的提离距离来提高检测能力。

4)随着检测能力的提高，检测实验的数据误差呈现逐渐降低的趋势。

5)本文建立的BP 神经网络的hit/miss 模型可实现不同检测条件下的检出/漏检预测，误差为0。

研究成果可为不同检测条件不同尺寸裂纹的检出/漏检研究提供理论指导，为该技术的工程应用奠定了基础。