基于图论的强人工干扰流域综合连通性量化的改进方法

杨 志，冯民权

(1.天津社会科学院资源环境与生态研究所，天津 300191； 2.西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048)

良好的流域连通性既是保障自然河流栖息地完整和生态系统健康的基础，也是城市水系发挥水文调蓄作用和水资源调度功能的前提，对具有自然-社会二元属性的强人工干扰流域具有重要意义。闸坝通过控制水流来除害兴利，但密集的闸坝群导致河道水体不流动、自净能力丧失、生态功能退化，这些对水系的完整性和河流的连通性造成极大破坏，亟待开展强人工干扰流域连通性恢复的相关研究。闸坝的建设与运用对河流生态环境产生胁迫作用，已成为水利、环境、生态等领域的共识[1]，要考察强人工干扰流域河网水系的变化过程，并对其流域连通性进行恢复，开展河网连通性量化研究是必不可少的。在理论内涵上，这部分研究起源于对河流景观连通性的探讨[2]，之后从多种角度被赋予地貌连通、水文连通和生物连通等丰富内涵，逐步发展成关于河流水生态系统结构及其相关功能的分析框架[3]。其中，根据生态系统的时空结构特征，河流连通性被划分为纵向、横向、垂向和时间4个维度[4]，从功能角度被描述为源、汇、滞后、转化和避难等[5]。随着对流域连通性认识的不断深化，其内涵体系逐渐发展，但至今尚无定论。在量化方法上，现阶段通常以水系格局作为切入点[6-7]，从边连通度、点连通度[8]或水文连通[9]的角度评估河网的连通性。以上手段推动了河网连通性定量分析工作，然而对于实际环境而言，河网行洪性能还与河道的种类有着紧密联系。针对不同河道之间输水能力差异性[10-11]，基于河道水流阻力和洪峰流量[12]的河网加权连通性定量评价方法应运而生。徐光来等[13]利用以水力阻力和图论为基础的河网连通性考察策略，采用水流阻力的倒数量化反映河流的顺畅程度。Grill等[14]进一步探索了分层和动态的河流系统的连通性，建立了基于流量的河流破碎化指数和河流调节指数。上述研究从水流阻力、水位或水质参数等单因素量化河网连通性，而实际上河流的连通性受水文、水动力、水质和人类活动等多方面因素的影响。

河网图模型可用于流域研究的诸多方面，如水文模拟中水流方向[15]和流域边界的确定[16]、生态保护区的选择[17]及其网络优化[18]以及河网栖息地[19]、河道-滩区系统[20]和多闸坝流域[21]的连通性分析等。其中，水利工程影响下的流域连通性量化常采用纵向连通性指数法、累积法、瓶颈法、树状水系连通性指数(dendritic connectivity index，DCI)法和生物迁移能力法。纵向连通性指数法关注单位长度上的人工建筑物个数，累积法[22]和瓶颈法[23]着重于生物对于障碍物的可通过性，分别从闸坝可通过能力和鱼类个体差异角度计算河流中多个障碍物组合通过率。DCI更为全面地分析了不同数量、可通过性及地理位置的闸坝对河网连通性的影响[24]。如Cote等[25]基于生物体能够在网络的两个随机点之间自由移动的期望概率，量化河流网络连接障碍的位置对树状水系连通性影响；Rincón等[26]提出了一种基于图论的闸坝移除优先次序求解方法，该方法考虑了闸坝群的上下游可通过能力；Grill等[27]引入了包含河流种类和河流迁徙连通性在内的改进河网连通性指数和河流监管指数，作为树状水系连通性和河流调节能力的衡量工具；Shaw等[28]提出了生物迁移能力法，将水力模型与连通性模型集成，探索树状水系中水力作用对连通性的驱动机制。此外，诸发文等[29]和马栋等[30]将闸门开启度概化为开启和关闭两个状态纳入模型，分别得到了改进的水流阻力法和边连通度法。然而，为了配合区域水资源利用需求，树枝状的天然水系逐渐向人工渠系纵横交错的网络化河流系统转化，河段之间的连通路径不再具备唯一性，传统的河网连通性量化方法不再适用，改进的方法要考虑到水利工程与河流生态系统复杂的交互影响，有待深入研究。

综上所述，现有河网连通性研究存在两方面不足。一方面，相关研究多依赖图论中对于顶点、边、拓扑特征和连通度的基本概念，或借鉴道路网络中连通性的判别指标，虽已有将图论结合水流阻力、水位和水质参数等进行河网连通性评估的研究，但考虑因素均比较单一，而河流的连通性受水文、水动力、水质和人类活动等多方面因素的影响，因此需要一个更加全面的方法对河网的连通性进行综合性评估。另一方面，城市河网为满足局部调水、景观蓄水、生产生活和防洪等多重需求，在整体上呈现出河道人工化、水系网络化、河流碎片化、闸坝密集而利用率不高的现象。DCI可兼顾水利工程的数量、可通过性及地理位置对连通性的影响，但在网状水系中无法直接应用。

基于上述认识，本研究将DCI方法与最短路径思想结合，以格网状水系中任意顶点间的最短路径代替树状水系中的唯一路径，得到改进的网状水系连通性指数(reticulate connectivity index，RCI)法。并通过测算一个涵盖水文、水动力、水质和水生态要素的综合阻力权(comprehensive resistance weight，CRW)，进一步提出改进的河网综合连通性指数(comprehensive connectivity index，CCI)法。选取淮河流域沙颍河水系污染最为严重的清潩河流域作为研究实例，该流域存在水利工程繁多、碎片化严重、河流连通性遭受破坏等情况，面临水系不通畅、水体不流动、污染物阻滞、自净能力丧失、生态功能退化等问题，是典型的强人工干扰流域，亟待开展流域连通性恢复的相关研究。以此为例，研究上述方法在强人工干扰流域河网综合连通性量化及恢复中的应用，以期为类似流域的连通性量化和恢复提供科学依据和决策参考。

1 研究区概况与数据来源

1.1 研究区概况

清潩河属淮河流域沙颍河水系，位于东经 113°03′～114°19′、北纬33°42′～34°24′之间，全长149 km，流域面积2 362 km2。清潩河流经新郑市、长葛市、许昌市、临颍县、鄢陵县等市县，是典型的强人工干扰流域，仅干流就有12闸2坝。流域内主要支流包括石梁河、小泥河、小洪河、外沟河、黄龙渠、鸡爪沟等(图1)。

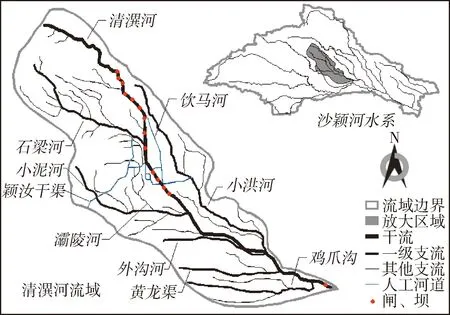
图1 清潩河流域示意图

颍汝干渠和饮马河是清潩河流域内的两条主要人工河流。流域内天然径流匮乏，用水有赖于外调水源的补给，颍汝干渠是调水的主要渠道。饮马河是在天然水系的基础上连接拓挖而来，现主要承担景观娱乐功能，其主要水源同样来自调水。为了满足调水和水源分配等需求，清潩河流域内有大小水工建筑物104座，其中管涵和箱涵共31座，溢流堰10座，溢流坝1座，橡胶坝3座，跌坎1座，北海提水泵站1座，其余大小水闸57座，多集中在小泥河汇入清潩河之前的市区段。流域内涵洞主要用于过水，考虑到水工建筑物的水流调节性能，仅将水闸、橡胶坝和提水泵站作为调控节点，并将距离1 000 m以内的两个节点进行合并处理，概化后流域内有闸坝节点47个，另有源汇和湖泊等其他节点14个，共计61个，如图2所示。

图2 清潩河流域闸坝分布

1.2 数据来源

水系图通过地理空间数据中心的数字高程模型(digital elevation model，DEM)数据自动提取，并根据河南省地图院提供的水系图进行校正；河段的长度和水域面积通过ArcGIS从DEM数据中进行提取；水文和水质基础数据来源于水文年鉴、环境统计年鉴和污染源调查数据，各节点的流速和污染物质浓度通过数值模拟计算求得；描述闸坝过流能力的系数通过历史研究从文献中确定。

2 研究方法

2.1 RCI计算方法

RCI是一种根据水利工程的数量、可通过能力及地理位置量化河网连通能力的方法。将两河段之间闸坝数量最少的一条通路，称之为易达路径。RCI取决于河网中任意两点之间易达路径的闸坝的数量、可通过能力以及河段水域面积，可视为任意两河段间的易达路径的连通性的总和。通过图模型的转化和易达路径的连通性计算，进而求解网状水系的连通性。RCI在Cote等[25]提出的DCI基础上，以易达路径替代树状水系中河段间的唯一通路，得到水利工程分割作用最小的河网通路；并采用水域面积占比代替DCI中的河段长度占比，将湖泊、湿地、河流与人工小型沟渠的水域贡献加以区别；进而将强人工干扰流域中水利工程干扰和水域侵占等人类活动的影响纳入河流连通性的量化评估。

a. 河网图模型的转化方式。针对流域内河道的不同交汇情况，采用如下转化方式(图3)，将以闸坝为顶点、以河段为边的有向河网图模型(图2)，转化为以河段为顶点、以闸坝为边的河网有向图模型。由图3可见：①情况1，沿水流方向，若河流a始于河源Y1，经过闸G2，终于河口H3，节点将河流分为河段R1和河段R2，则概化为河段R1经过闸G2，流至河段R2；②情况2，沿水流方向，若河流a与河流b分别经过闸G1和闸G2后，交汇于闸G3处并合并为河流c，则概化为河流a经过闸G1和闸G3，河流b经过闸G2和闸G3，之后两河流交汇；③情况3，沿水流方向，若河流a经闸G1后分流为河流b与河流c，之后河流b与河流c分别经闸G2和闸G3下泄，则概化为河流b经过闸G1和闸G2下泄，河流c经过闸G1和闸G3下泄；④情况4，沿水流方向，若河流a与河流b分别经闸G1和闸G2后交汇于一点，形成河流c后经闸G4下泄，则需将交汇点前的两河段分别与交汇后的河段进行合并，形成两个新的河段；⑤情况5，沿水流方向，若河流a经闸G1后于一点分流为河流b与河流c，之后河流b与河流c分别经闸G3和闸G4下泄，则需将交汇点前的河段与交汇后的两河段分别进行合并，形成两个新的河段。

图3 转化规则示意图

b. RCI计算公式。采用邻接矩阵A表示转化后的河网有向图模型，其中0元素表示相邻河段上无闸坝，1元素表示相邻河段上有闸坝。采用最短路径算法推求任意两河段之间的易达路径，计算公式为

(1)

其中

式中：IRC为RCI值；n为河段的数量；Si与Sj分别为河段i与河段j的水域面积；S为河网水域的总面积；指数乘以100是为了将IRC的值调整为0～100之间，其值越高，表明连通状况越好；cij为河段i与河段j间易达路径的连通性，取决于易达路径的闸坝数量(Mmin)和可通过能力[31]；pmu为生物体从下游至上游通过易达路径的中第m个闸坝的能力；pmd为生物体从上游至下游通过易达路径的中第m个闸坝的能力。

2.2 CCI计算方法

人为因素作用下的闸坝、渠系和湖泊群等改变了流域纵向、横向、垂向和时间维度的水系结构，导致水域面积、流场结构、污染物质分布和水生动植物多样性的改变，即流域水文、水动力、水质和水生态要素的时空分布都发生了变化，从而影响流域发挥源、汇、滞后、转化和避难等系列功能。因此，强人工干扰流域连通性应贯穿于结构层、要素层和功能层之中，承上启下的要素层是连通性量化的关键。CCI是一种涵盖水文、水动力、水质和水生态要素的河网综合连通性量化方法，该方法可相对全面地评估水域面积萎缩、环境流量匮乏、水质污染严重、生物通行困难的强人工干扰流域的综合连通性。该方法基于图的连通性原理，结合最短路径思想，将流域最大综合连通性问题转化为最小综合阻力问题。在2.1节的基础上，寻求一个涵盖水文阻力项、水动力阻力项、水质阻力项和水生态阻力项的CRW，以此作为边的权值，推求对河流连通性综合阻碍作用最小的路径，弥补了以往研究中考虑因素单一的不足。

a. 水文阻力项采用平均水面宽[31]的倒数表示，计算公式为

(2)

式中：αij为水文阻力项；Sij为相邻顶点i和j之间的河段的水面面积；Lij为相邻顶点i和j之间的河段的长度。Sij和Lij的比值越大，说明该河段上的水域面积越大，以此可以将湖泊和湿地纳入系统并与河道相区别。αij采用该比值的倒数描述该河段上的水域丰富程度，即αij越小，河段水域面积越大，所面临的水文阻力越小；αij越大，河段水域面积越小，所面临的水文阻力越大。

b. 水动力阻力项采用流动时间[6]衡量，计算公式为

(3)

式中：βij为水动力阻力项；Tij为水流通过河段ij所需要的时间；Vij为河段ij的平均流速。βij越小，河段流动能力越强；βij越大，河段流动能力越差。

c. 水质阻力项取决于污染物质浓度[32]，良好的水质是河流有效连通并发挥生态功能的基础。借鉴Pringle等[32]对于水文连通度与污染物响应机制的探讨以及崔广柏等[33]纳入水质改善度的水系连通性评价指标体系，将水质阻力纳入综合阻力权，计算公式为

(4)

式中：γij为水质阻力项；ρijk为河段ij第k种污染物质的平均质量浓度(k=1，2，…，m)；m为污染物种类数。

d. 借鉴Clarkin等[31]提出的闸坝可通过能力系数，将其修改为闸坝的阻碍作用系数，用以定量描述该河段的人类活动方面的阻力。鉴于研究区域的数据可获取性，水生态阻力项仅通过水利工程对水生生物的阻碍作用进行量化，采用闸坝对生物体通行能力的阻碍作用系数[31]加以描述。计算公式为

(5)

式中：ωij为水生态阻力项；a1u和a2u为建设闸坝使生物体从下游至上游通过某个顶点的难度增加的一个系数；a1d和a2d为建设闸坝使生物体从上游至下游通过某个顶点的难度增加的一个系数；b为河段ij的起始顶点和结束顶点中闸坝顶点的数量，b=0，1，2。a1u、a2u、a1d、a2d均不小于1，a1u、a2u、a1d、a2d越接近1，说明闸坝对河网系统过流能力的影响越小，越接近天然状态。

结合4种阻力项，CRW值的计算公式为

(6)

式中:Wij为河段ij的CRW值。水文阻力项、水动力阻力项和水质阻力项均采用河段的该项系数与河网全部河段该项系数之和的比值表示，旨在避免不同量纲的影响，将水文、水动力和水质项均转化为0～1之间的系数，使得计算结果具有可比性。

利用式(6)计算任意河段间的CRW，作为边的权重，建立河网综合阻力权的加权邻接矩阵，将河网连通性问题转化为加权邻接矩阵的最短路问题。采用最短路计算方法，求得最小综合阻力矩阵；第i个顶点的最小综合阻力描述为以该顶点为起始点和结束点的最短路径之和；河网最小综合阻力描述为河网中全部顶点的最小综合阻力之和，即河网的最大综合连通性，CCI采用该值的倒数进行描述。

在上述基础上，依次去掉河网内任意一个或多个闸坝，修改相应的闸坝顶点为普通顶点，即修改b的取值，进而改变相关河段的ωij取值，重新计算新的CCI。通过比较计算结果，将CCI由大到小排列，排列越靠前说明该闸坝的去除对水系连通性的提高贡献越大，据此可确定单一闸坝的优先去除次序以及去除多个闸坝的优化组合方式，获得去除效果最好的方案，对闸控河网的综合连通性进行优化。

3 结果与分析

3.1 RCI计算结果

采用图3中的概化方式，将图2中的河网概化为以河段为顶点、以闸坝为边的河网有向图模型。水域面积与水位密切相关，可采用最大水位、正常蓄水位和实测水位下的水域面积分别表示河道的极限蓄水能力、日常蓄水状况和水系的实际水域面积，利用ArcGIS提取实际水域面积参与计算。分别计算闸坝的可通过能力p从0增加到1的RCI值(图4)。由图4可见，随着闸坝可通过能力的增加，RCI值也逐渐增加，并且幅度越来越大。参考文献[31]，p取0.8，计算得该网状水系的RCI值为1.88。逐一去掉河网中的任何一个闸坝，计算得到相应的RCI值。

图4 RCI值与p 的响应关系

3.2 CCI计算结果

利用ArcGIS从DEM数据中提取Sij和Lij，求得α；通过水动力水质模拟计算求得各节点的流速、COD和氨氮质量浓度的变化过程，取河段ij两端节点的模拟过程的平均值(图5)，计算该河段的β和γ；a1u、a2u、a1d和a2d取闸坝可通过能力的倒数，为1.25，进而确定ω。建立河网加权的邻接矩阵，采用最短路径计算方法，求得最小阻力矩阵，进而得到河网的CCI值为26.13。在此基础上，逐一去掉河网中任一个闸坝，分别计算得到相应的RCI值和CCI值见图6，可见任何一个闸坝的去除均使得河网连通性有所提高。去除后的CCI值在26.13～30.00之间，其中25、26、28和29号闸门去除后的连通性增幅达到10%以上(图7)。将逐一去除单个闸坝后的RCI值和CCI值从大到小排序，将前20位的闸坝序号与排名绘制成图8，其中有11座闸坝共同出现在两种方法的前20位中，其中6个排名差距在5名以内，说明两种方法对闸坝重要性的判断在趋势上具有一致性。

图5 流速和污染物质量浓度的平均值

图6 去除单一闸坝后的RCI值和CCI值

图7 去除不同闸坝后的CCI值变化

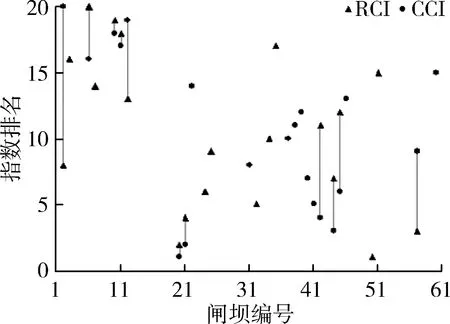
图8 闸坝去除后的RCI值和CCI值对比

4 讨 论

清潩河流域的闸坝主要具有防洪、供水和景观功能。清潩河和灞陵河上的闸坝需承担防洪任务；颖汝干渠及沿线闸坝的主要功能是将颖汝干渠调来的北汝河水源输送到城区段各个水系；其他支流上的闸坝主要发挥景观功能，满足景观蓄水水面要求。根据连通性计算结果，选取去除后河网连通性提高显著的闸坝，并结合区域内供水和用水需求，针对不涉及防洪任务、分布过密且功能重复的闸坝，拟定以下5组优化方案(表1)。由表1可见，分布在颖汝干渠供水线路上的24、25、26、27、28、29、30、32和47号闸坝，其主要功能是控制供水流量，且供水线路间存在一定的重复性，对此拟定第1、2、3、4组方案。分布在饮马河上的54和55号闸坝，主要用于蓄水保持景观水面，且分布集中，对此拟定第5组方案。

表1 使用CCI进行清潩河流域河网连通性恢复

第1组：颍汝干渠通过30-40和29-47-40向灞陵河40节点供水，两条线路同为控制调水所用，且相距较近，可保留其一。去除闸坝30、去除闸坝29和47后的CCI值分别为26.22、29.15，后者增幅达11.55%，改善显著。

第2组：颍汝干渠通过29-47-42和27-43向灞陵河和霸陵湖供水，两条线路同为控制调水所用，且相距较近，可保留其一。去除闸坝29和47、去除闸坝27后的CCI值分别为29.15、27.70，前者改善效果更为显著。

第3组：颍汝干渠通过25-33和24-32-33向小泥河供水，两条线路同为控制调水所用，且相距较近，可保留其一。去除闸坝25、去除闸坝24和32后的CCI值分别为29.34、26.73，前者改善效果更为显著。

第4组：颍汝干渠26-27-28段，通过3个水闸控制供水水量，但颍汝干渠沿线闸坝众多，所涉及小泥河、长店沟、灞陵河支流、灞陵河和石梁河均有水闸直接控制供水，除27闸直接控制长店沟引水外，闸26和28相距较近，将颍汝干渠分为上下两段控制其水量分布，因此闸26和28可保留一个，计算结果表明，去掉闸28后的CCI值为30.00，改善效果更为明显。

第5组：饮马河52-53-54-55-56段闸坝稠密，其中闸52和53控制东湖饮水河泄水，闸56控制许扶运河引水，因此考虑去除闸54或将两者均去除，结果表明二者均比原河网CCI值有所提高，后者增幅略高。

综上，取各组方案中连通性改善效果较好的方案，同时去除闸25、28、29、47、54和55，河网CCI值从26.13提高至38.34，增幅达46.73%，效果显著。在实际应用过程中，可在流域闸坝调度方案中，对上述闸坝采取全开泄流或减少使用频率等方式，弱化其对河网连通性的阻碍作用。本研究尝试结合许昌水务部门的实际工作，将表1中建议去除的闸坝，采取弱化其影响的方法应用于《清潩河(许昌段)流域河湖水系2017—2018年度环境流量调控方案》，通过实际应用，该调度方案可以满足许昌市的调度需求，取得了一定的示范效果。这一应用从实践中支持了恢复流域天然属性这一理念，但对于恢复措施还只是初步探索阶段，对于方法的完善和应用的深化，未来仍有很大的研究空间。

5 结 论

a. 提出了两种适用于格网状水系连通性量化的改进方法。RCI法针对天然树状水系与人工渠系交织后的网状水系，将河网和闸坝系统概化为以河段为节点、以闸坝为边的河网有向图模型，并结合DCI与最短路径思想求解，拓展了应用范围。CCI法将河网闸坝系统概化为以闸坝为节点、以河段为边的河网有向图模型，通过测算涵盖水文、水动力、水质和水生态阻力项的CRW，弥补了以往河网连通性量化方法中考虑因素单一的不足。

b. 以强人工干扰的清潩河流域为例，采用RCI法和CCI法优化其闸控河网的连通性。结果表明两种方法对单一闸坝重要性的判断在趋势上具有一致性，去除单一闸坝后的CCI值在26.13～30.00之间。5组闸坝组合对照方案的结果表明，最优组合为同时去除闸25、28、29、47、54和55，优化后河网的CCI值从现状的26.13提高至38.34，增幅达46.73%，连通性改善效果显著。

c. RCI法和CCI法均可用于网状水系连通程度的定量分析和闸坝系统的全局优化，树状水系亦然，前者对水利工程作用更具针对性，后者更适合河流连通性的综合评价，结果可用于流域健康评估、水系连通工程设计和闸坝调度方案优化等领域。本研究着重于河网闸坝系统与流域连通性响应关系研究，闸坝可通过能力的取值相对简单概化，闸坝的数量、规模与生物体的种类、数量之间的量化关系和反应机制，仍有待进一步开展调研和试验研究。