分层型河口咸水上溯对径流潮汐共同作用的基本响应

尹小玲，赵雪峰，黄舒琴，卢 陈

(1.华南理工大学土木与交通学院，广东 广州 510640； 2.水利部珠江河口动力学及伴生过程调控重点实验室，广东 广州 510611)

潮汐河口咸水上溯受径流和潮汐的影响，其变化规律对河口水环境和生态过程的发展十分重要，了解和掌握这些规律可为咸潮控制措施提供可靠的参考和指导。早期研究把上溯距离和径流量关联成指数关系，其中指数为负值，直接反映了宏观上径流对咸水上溯的抑制作用[1-3]。随着研究的不断深入，人们进一步认识到河口咸水结构具备自我调整机制以适应外部环境的改变，并且咸水运动变化具有明显的时间效应，河口咸水调整时间作为估量潮平均盐度分布偏离平衡态的评价指标，代表咸水适应新状态的时间尺度[4-5]，该尺度可以短到1 d，也可以长过1a[6]。调整过程中，与径流相关的重力环流和潮汐的混合与离散作用对盐输运的贡献非常关键，两者耦合变化导致河口内盐总量增减变化[7]。河口观测和盐平衡模型分析表明，一些中等规模的部分分层河口在小径流情况下混合增强，咸水入侵距离虽然较大但其潮平均值的变化却十分有限[8-10]，而一些大江大河的入海河口在低径流时段常常有着较高的分层指数，具有更突出的时效相关特征[11-13]，其非线性过程可能导致不一样的表现，如枯季珠江磨刀门河口在小径流量下半月周期咸界变化具有更大的变幅[14]。由此可见，除了地域特性外，河口内部所发生的混合、分层和环流过程非线性地依赖外部的径流潮汐共同作用，而径流和潮汐自身的变化常常处于多种时间尺度下，因此，河口咸水运动对径流潮汐共同作用的响应过程和时空变化将十分复杂[15-16]。然而对径流潮汐共同作用影响的探讨以往分析主要集中在大小潮的线性对应过程上[17-18]，径流主导的分层型河口半月周期非线性连续变化的普遍机制仍有待深入研究。

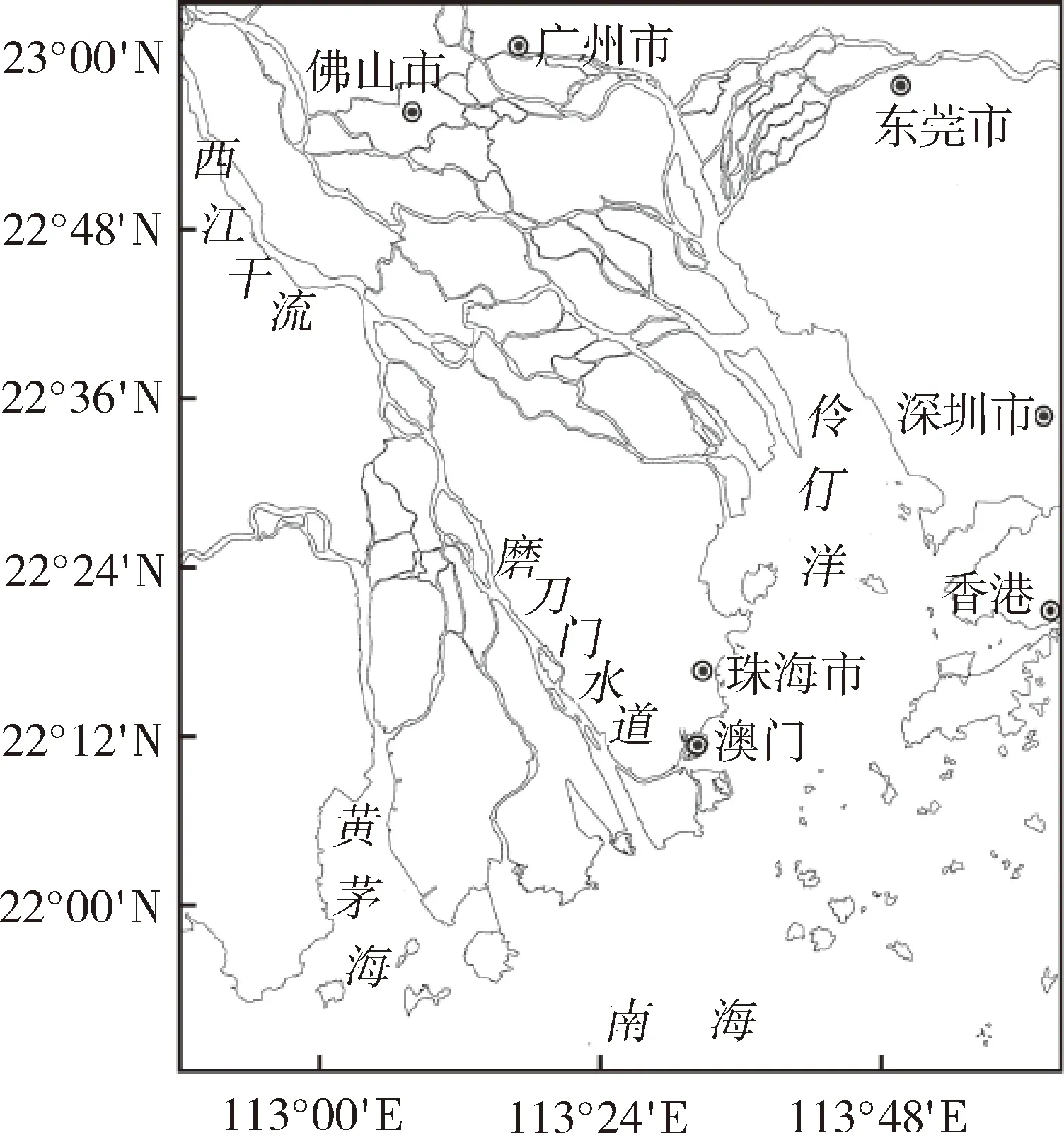
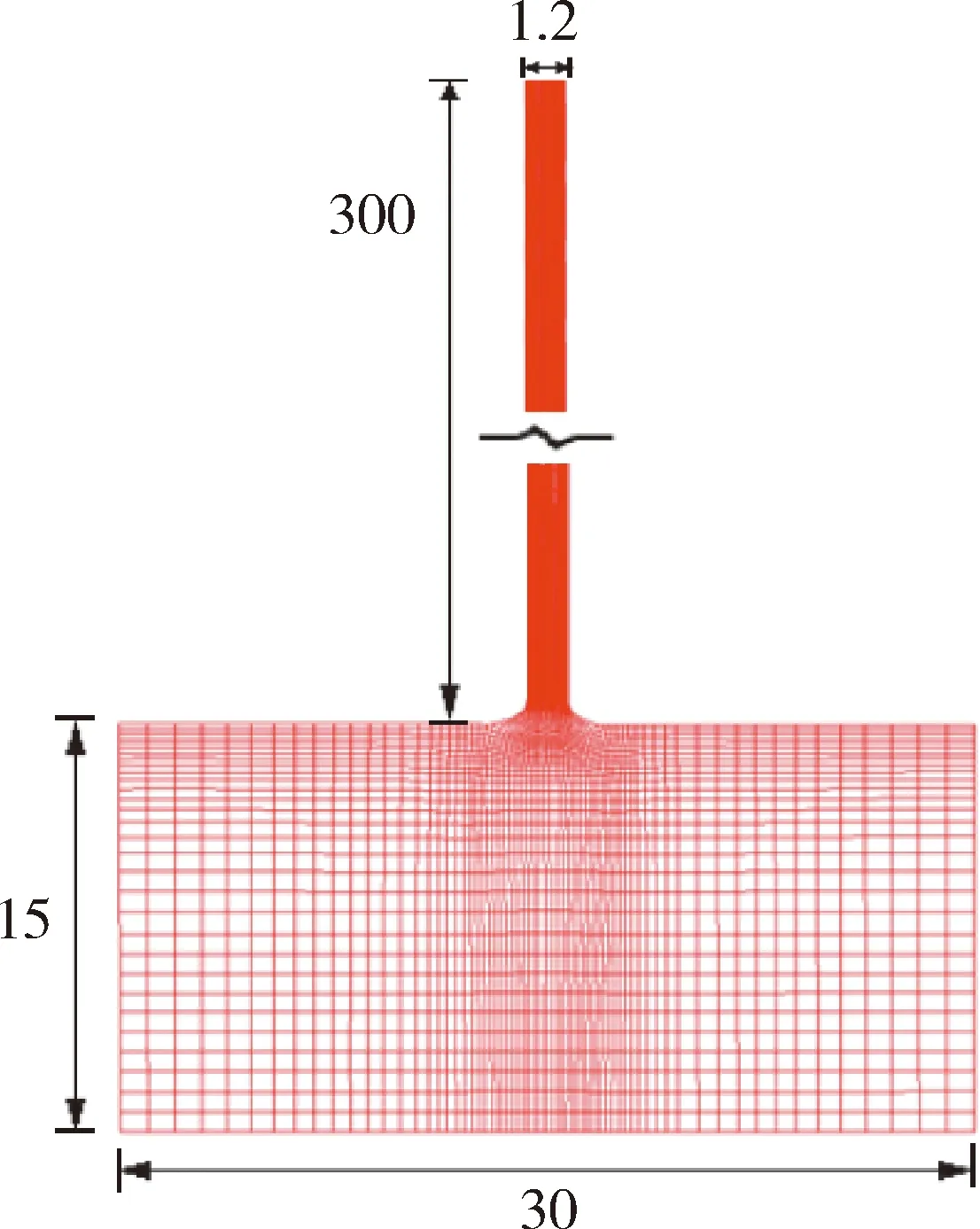
(a) 平面位置 (b) 概化河口计算网格(单位：km)

采用概化河口是很多研究者在研究河口基本规律时常用的手段之一[3，19-21]，其优势在于突出主要动力作用的物理过程，简化复杂地形的影响。因此，本文针对径流潮汐共同作用下径流主导分层的大型河口，采用概化河口进行水动力三维数值模拟试验，探讨半月周期咸水运动对径流量变化的响应，以及半月周期咸水上溯的演化过程和机制，由此掌握上游工程增流压咸的适当时机。

1 数值试验方法

选取南海潮波作为潮汐动力过程，参考入汇南海的珠江磨刀门河口的宏观几何条件建立概化河口。磨刀门河口如图1(a)所示，是西江入海的主要通道，上游径流枯季多年平均流量达2 058 m3/s，多年平均潮差最大值、最小值和平均值分别为2.0 m、0.6 m和0.86 m，因此属弱潮径流型河口，水道宽度变化不显著，断面平均水深约为8 m。同时，它也是典型的分层型河口，枯季径流量大幅下降，潮区界距口门可达300 km，咸水分层明显，上溯入侵显著增强，周围网河对咸水运动影响较小[14，22]。因此，磨刀门作为径流潮汐长期作用下的大型冲积河口，其枯季咸水过程对径流主导的分层型河口具有较好的代表性。

概化河口的感潮河道长300 km，断面为矩形，宽1 200 m。口外海域范围纵向取至30 m水深处，横向长度为纵向2倍，口内外底坡分别根据原型实际情况取平均值。数值计算采用Delft 3D程序的水动力模块，计算网格平面如图1(b)所示，垂向分为10层。上游开边界设为流量过程，盐度为0 psu，下游开边界以南海主要分潮K1、O1、M2和S2驱动，盐度设为30 psu。曼宁阻力系数在口外取为0.020，口内为0.025，流场计算中采用了k-ε紊动模型。试验先在零水深、零盐度条件下冷启动，预热计算1个月，其结果作为试验热启动的初始条件，然后模拟计算1个月。所有试验条件在磨刀门河口实际情况基础上适当扩展范围，河口横向变化在此忽略不计。

2 结果与讨论

2.1 准平衡态试验

当河口边界条件的潮周期过程恒定时，咸水运动和盐度分布可以达到涨落过程稳定(或称为准平衡态)。本文准平衡态试验采用等潮差正弦潮和恒定上游径流驱动，其他计算参数保持不变，模拟计算10 d后盐度分布及其变化在每一潮周期内已基本一致，即达到准平衡态。以底层0.5 psu等盐线在潮周期内到达的最远距离作为该日咸水最大上溯距离即咸界，准平衡态下每日最大上溯距离是一个对应边界条件的恒定平衡值。模型验证分析见文献[23]。

准平衡态试验分全日潮和半日潮，为保证试验结果合理，河道水深试验范围在6～12 m，上游径流量试验范围在900～3 800 m3/s，外海潮差试验范围在0～3.5 m。其中水深为6 m的试验结果见图2，其他水深情况趋势与此相似，径流量Q=2 200 m3/s时不同水深两种周期计算的平均结果如图3所示。由图2可见：①全日潮最大上溯距离大于半日潮；②相同水深条件下，上溯距离在小潮差时对径流变化敏感，在小径流量时对潮差变化敏感，反之亦然；③当潮差大于1.5 m后上溯距离对径流和潮差变化响应都减弱。由图3可见，相同流量条件下，水深越大，咸水越容易上溯，并且这一特征在小潮差更明显。

(a) 全日潮

(b) 半日潮

图3 不同水深准平衡态下最大上溯距离

Hansen等[24]提出的分层系数N可反映盐度分层或混合程度，N值越大，分层越显著。试验中在全日潮咸界一半的位置计算断面分层系数，结果显示，潮差为0.5～2.0 m时，N值范围在1.5～2.0，属于高分层型；潮差为2.0～2.5时，N值为0.5左右，属于部分分层型。同条件下半日潮N值普遍小于全日潮，咸水混合程度相对更高一些。

2.2 半月周期咸水上溯特性

半月周期咸水运动试验中，外海边界采用南海主要分潮K1、O1、M2和S2的潮位过程，是典型全日、半日混合潮型，上游边界仍采用恒定径流过程。图4为径流量Q=2 200 m3/s且河道水深8 m时试验的代表性结果，其中正弦潮曲线为全日潮和半日潮准平衡态结果进行平均得到，是一条单调曲线；分潮曲线为半月周期分潮驱动的非平衡态结果，是一条逐日变化的多值曲线。由图4可见，非平衡态的分潮曲线呈现为顺时针围绕准平衡态正弦潮曲线变化的绳套曲线。

图4 正弦潮和分潮条件下最大上溯距离

图4显示，大潮期潮差大于2.0 m后，咸水最大上溯距离十分接近平衡值。随着大潮转小潮，最大上溯距离随平衡值趋势开始上升但有所滞后，绳套曲线处于平衡曲线下方。随着平衡曲线陡度增加，两者差距越来越大，及至第13日最小潮时咸水也未完成调整到达准平衡位置。之后随潮差开始增大，咸界虽继续上升但仍未达到平衡位置，如第14日情况。随着咸界平衡值继续快速下降，绳套曲线穿越平衡曲线后开始下降，但仍滞后于平衡曲线，直到大潮期来临复又进入下一个半月周期过程。由此看到，随着半月周期内潮差持续变化，由于时滞影响，小潮期到大潮期与大潮期到小潮期的咸水运动并不是等同的反向过程，咸水在最小潮和最大潮也没有完全达到准平衡态，而是处于不断调整之中，即每日最大上溯距离在半月周期的最大值和最小值并没有分别对应小潮和大潮，而是滞后1～3 d。这种咸水上溯距离随潮差变化的绳套关系实质上反映了自然物理过程中非平衡态的非线性关系，以及非平衡态向平衡态趋近的滞后进程。

2.3 分层咸水的混合状态

对潮周期平均过程采用分层理查森数RiL分析混合状态[5]，计算公式为

(1)

式中：g为重力加速度，m/s2；H为水深，m；ρb、ρt分别为底层和表层水的密度，kg/m3；ρ0为淡水密度，kg/m3；UT为潮周期垂线平均潮流幅值，m/s。RiL值越小，代表分层较弱而混合较强，反之亦然。口门内不同距离断面位置RiL的计算结果如图5所示。

(a) 距口门20 km

(b) 距口门15 km

(c) 距口门10 km

(d) 距口门5 km

图5中，整体上小潮期分层比大潮期更显著。更值得注意的是，小潮前后的中潮分层情况并不相同，小潮前RiL值小于小潮后，准平衡态情况居中，即与准平衡态相比，小潮前混合更强而分层更弱，小潮后则相反，并且这一特征越向口内咸水头部方向越明显。大潮期RiL值差别相对较小，同时咸水头部的混合程度比口门附近明显更高，RiL值达到0.01左右。

大小潮RiL值的变化过程与图4中绳套曲线和平衡曲线的相对位置基本对应，反映了盐度分层混合状态在小潮前后不同中潮时段存在不同的发展特点，以及混合过程依赖时间非线性变化的特性，但还不能解释咸潮最大、最小入侵分别滞后小潮、大潮1～3 d的现象，因此还需要结合径流以及盐输运过程进一步分析。

2.4 盐输运量变化

一般情况下，河口盐输运过程可以体现各种动力因素作用的综合效果，反映通过断面的盐量净输移方向和随时间的增减变化。为了解咸水上溯距离与盐输运过程内在联系，并考虑到棱柱形河道横向变化有限，因此计算分析单宽盐输运量Fs，其逐日值计算公式为

(2)

式中：T为统计周期总时长，s；M为周期内统计时段数；N为垂向分层数，本试验均分为10层；H为水深；Hi为i时段水深，m；s为空间分布的盐度，psu；u为空间分布的流速，m/s；sij、uij分别为i时段j层的盐度和流速，流速向陆为正，向海为负；z为空间垂向坐标，t为时间坐标。本文计算针对潮周期，T取86 400 s，M取24。

以径流量为1 400 m3/s和3 000 m3/s的分潮试验为例，图6为距离口门10 km处垂线单宽盐输运量逐日变化过程。结合咸水分层混合情况看，小径流量下，大潮期混合强烈，大量底层盐分被带往上层，径流作用使得盐输运向海，口内盐总量逐日减少，至大潮后1～2 d盐输运量才逐渐由负值转为正值，即输运方向开始由向海转为向陆，对应咸水上溯距离达到半月周期最小值。此后随着潮差日渐减小，混合程度下降，向陆盐输运量不断增长，也意味着被径流带出口外的部分相对减少，该过程在中潮达到峰值后逐日回落，至小潮期向陆盐输运仍然存在，口内盐总量仍在继续增加，及至小潮后2 d左右，盐输运量才由正值转为负值，此时口内盐总量积累达到最大，对应的咸水上溯距离亦达到半月周期内最大值。中潮至大潮，盐向海输运量很快增大到最大值然后逐日减小，口内盐总量不断减少，咸界后退，完成一个半月周期的变化过程。大径流量时，总体变化过程与小径流量情况相似，但向陆盐输运量更小，大潮附近接近输运平衡的时段更长。由此可见，盐输运量的逐日变化与每日咸水最大上溯距离的发展呈现显著对应关系。

(a) Q=1 400 m3/s

(b) Q=3 000 m3/s

同时，相同的中潮潮差对应着不同的盐输运方向，小潮前后分别向陆和向海。结合图5中咸水上段的RiL值特点可知，大潮后尽管盐输运开始向陆，但咸水混合仍然较强，上层径流在落流时段带走相当的盐分造成咸水上溯距离增大比准平衡态慢；而小潮后的中潮期盐输运虽然开始向海，但混合尚弱，需要一定时间发展，此时径流挟带入海的盐量较少，咸水上溯距离减小比准平衡态慢，因此出现图4中非平衡态绳套曲线围绕平衡曲线顺时针方向发展的情况。

2.5 径流量对咸水上溯距离的影响

图7(a)为不同径流量条件下分潮试验结果。径流较小时，咸界半月进退摆幅较大，最大可达28.7 km，绳套形态圆润；径流较大时，咸界摆幅最大值下降为11.9 km，绳套形态扁平，这种变化趋势与图2中不同径流条件的准平衡态曲线特点相适应。按照河口咸水调整时间尺度的概念，小径流量下非平衡态与准平衡态的差距更大，调整所需时间更长，图7(a)较好地反映了这一规律性。

图7(a)还显示，径流量越小，咸水迅速退落发生得越晚，并且在接近大潮期即使潮差变化很小，咸界退落也很迅速，一日之内可退落10 km左右，类似现象在磨刀门实际过程中也可观察到。

(a) 绳套曲线

(b) 时间过程

如果从图7(b)上溯距离随潮差发展过程看，咸水进侵阶段为8～9 d，而退落阶段则为5～6 d；在进侵开始阶段上溯距离对径流量响应相对较弱，小潮后对径流量响应逐渐增强；径流量越小，最大及最小值出现的时间越滞后，所需消退时间越长，反之亦然。径流量达到2 200 m3/s以上时上溯距离才能基本保持在40 km以下，结合试验条件看，与以往实际情况的研究结论相近[14]。

2.6 增流压咸方案模拟

综合咸水运动过程与时间相关或与前期状态相关的显著特点，可以推断，上游增流压咸措施在大潮期及其后中潮时段发挥效果有限，而在小潮期及其后中潮的咸水快速上溯时段能起到较大作用，但需要持续保持较大流量直到大潮来临，在大潮转小潮期间可停止增流，以充分利用咸潮退落的自然规律。由此可建立增流流量控制方案的基本框架，为上游工程实施压咸措施提供参考。

流量控制初步方案设计如下：河道水深设为 8 m，模型在径流量为1 400 m3/s的分潮试验基础上先运行，当小潮到来时梯级变化至2 200 m3/s，恒定持续7 d至大潮，复又梯级回落至1 400 m3/s，模拟计算时间包含大小潮共23 d。图8为方案模拟计算的逐日咸水最大上溯距离变化过程，为对比起见，也给出了径流量分别为1 400 m3/s和2 200 m3/s的计算结果。可以看出，增大径流量后，上溯距离开始下降，下降幅度日渐增大，小潮后最远咸界从51.0 km降至41.8 km，降幅为9.2 km；至咸潮退落中期压咸效果最为突出，上溯距离由46.8 km减至21.4 km，降幅达25.4 km。不仅如此，在距口门20 km的上游河段，咸潮影响时间也明显缩短，上溯超过40 km的时间由5 d减为4 d，超过30 km的由8 d减为6 d，超过25 km的则减少了3 d。因此，本流量控制方案可使口门以上40 km河段基本不受咸潮影响，即使是影响范围内的断面，受影响时间也有所减少，并且径流量增流时间短，有利于上游在枯季实施工程性压咸措施。

图8 增流压咸控制方案最大上溯距离

3 结 论

a. 在径流主导的分层型河口，径流潮汐共同作用下，半月周期咸水逐日最大上溯距离表现为随潮差顺时针围绕准平衡态变化的绳套曲线，这是咸水运动在半月周期随潮汐以非平衡态围绕准平衡态进行自动调整的结果，该过程反映了半月周期下咸水最大入侵发生在小潮后而最小入侵发生在大潮或其后的一般发展规律。

b. 由于混合过程的时间效应，咸水运动的调整过程呈现非线性特征，小潮前后的盐度具有不同的混合状态，向陆盐输运量在小潮后2～3 d达到最大，向海盐输运量在大潮后1～2 d达到最大，与逐日最大上溯距离变化相对应。径流量越小，咸水和准平衡态的差距越大，小潮后强烈上溯的持续时间越长，大潮期退落也越迅速，反之亦然。

c. 模拟试验结果分析表明，根据半月周期咸水运动特性，上游增流压咸时段从小潮开始至大潮结束，既可取得明显效果，又能充分利用咸潮自然消退规律，节约枯季淡水资源。